潜伏式武器水下减速着陆运动仿真

练永庆,王昕晔,宋保维

(1.西北工业大学 航海学院,陕西 西安 710072;2.海军工程大学 兵器工程学院,湖北 武汉 430033;3.海军工程大学 核科学技术学院,湖北 武汉 430033)

随着深海技术的发展,深海区域逐渐成为海上斗争的主战场之一。深海潜伏式武器[1]等也逐渐登上该战场。潜伏式武器一般通过水下平台如潜艇进行运送,到达设定战场进行水下施放,然后依靠自身负浮力坐落海底潜伏待机。本文所研究的潜伏式武器因其水下负浮力较大,在坐落海底前运动速度较高,如不采用减速措施,则可能会因着陆冲击对武器造成破坏。为此本文提出了先用减速伞进行减速,然后用舱段分离的方法实现其安全着陆。本文主要针对该减速方法进行仿真研究。

潜伏式武器属于水下航行器[2-4]的一种。在类似潜伏式武器的大深度无动力航行器运动建模与仿真方面,国内仅见有关“蛟龙”号载人潜水器的无动力下潜上浮运动研究[5-6]。本文对潜伏式武器着陆前开伞减速以及武器两舱分离的运动过程进行数学建模,开展数值仿真计算,获得武器及其分离舱段的弹道,以此来探讨潜伏式武器采用减速伞减速并结合舱段分离的方法实现安全着陆的可行性及相关运动规律。

1 潜伏式武器开伞减速及分离着陆运动过程

本文研究的潜伏式武器(简称武器,以下同)为外形呈圆柱形、有负浮力的无动力载体。该武器从潜艇施放后直至分离前为一整体,在到达分离深度后可分离为2段:武器舱(内置导弹等武器)和压载舱(提供负浮力)。当武器从潜艇上分离后,在负浮力作用下进入稳定垂直下沉(压载舱指向海底),直至武器到达设定的开伞减速深度。从这时起至着陆前大致可以分为以下2个阶段(见图1):

①第一阶段为减速运动阶段,在该阶段当武器达到设定开伞深度时打开减速伞,武器开始减速向海底运动;

②第二阶段为分离阶段,在该阶段武器减速运动到达设定的分离深度时,武器舱和压载舱分离,武器舱在压载舱带动下,向海底运动直至安全着陆。

本文主要对以上2个阶段运动进行建模与仿真。为了简化建模过程,做以下假定:潜艇在静止条件下施放,不考虑水下海流的影响;武器在开伞后,减速伞及武器外形产生的流体阻力独立作用在武器上,不考虑两者之间的耦合。

图1 减速伞缓冲方案示意图

2 潜伏式武器水下开伞后的纵平面运动数学模型

2.1 建模坐标系

在运动建模与仿真中,采用2种坐标系:固定坐标系Oxyz,简称“定系”;运动坐标系O1x1y1z1,简称“动系”,如图2所示。

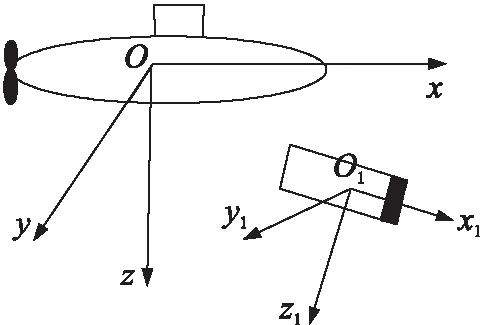
图2 固定坐标系和运动坐标系

定系Oxyz固定在地球,原点O选在施放瞬间潜艇与武器交界面上的某一点。Ox轴位于水平面上,以潜艇的主航向为正向;Oy轴位于Ox轴所在的水平面,按右手法则将Ox轴顺时针旋转90°;Oz轴垂直于xOy的坐标面,以指向地心为正。

动系O1x1y1z1固联于武器,随武器一起运动,原点O1取在武器的形心处。O1x1轴、O1y1轴和O1z1轴分别是经过武器形心的水线面、横剖面和纵中剖面的交线,正向按右手系的规定,即以O1x1轴指向武器的前部、O1y1轴指向右侧、O1z1轴指向水平龙骨为正,并认为O1x1、O1y1和O1z1是武器的惯性主轴。

2.2 开伞阶段的数学模型

在该阶段中,武器开伞前由于运动坐标系转动了-π/2(武器从潜艇上是水平施放的,施放开始时O1x1轴与Ox轴同向),所以此时武器的O1x1轴指向海底,在动坐标系,武器舱与压载舱可看作只存在O1x1轴方向的运动。经推导,开伞阶段的武器形心运动数学模型如下。

①x1轴向力方程。

(1)

②z1轴向力方程。

(2)

解以上方程可得在运动坐标系下的武器任一时刻形心的加速度,再经过坐标转换和积分即可知道固定坐标系下任一时刻潜伏式武器的位置:

(3)

(4)

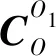
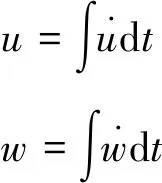
(5)

2.3 开伞过程流体阻力的计算

在第一阶段中,在武器减速伞打开后,其流体阻力Fa没有相应的经验公式来计算。对于这种情况,只能通过开展流场仿真计算来获取其仿真所需的流体阻力。

由于开伞是一个瞬态的过程,流场仿真实现难度较大,为此将开伞过程进行离散。对于开伞过程,对应某一给定的减速伞开伞角度,分别对其不同速度情况进行流场仿真,如此反复可获得不同开伞角度和流速条件下的武器整体所受的流体阻力。,再利用数表及插值的方法,即可获得各种情况下流体阻力数值。

武器开伞时的流场仿真的计算域如图3所示,整个区域形状为长方形。区域的对称轴与武器的对称轴重合。武器的前缘距流场入口宽度和长度均为模块宽度与长度的10倍以上。

图3 武器开伞流场仿真区域

进行流场仿真时,以RANS方程为控制方程,采用Standardk-ε湍流模型,用有限体积法对控制方程进行离散。压力-速度耦合迭代求解采用的是SIMPLE算法,压力项采用标准离散格式,动量、湍流动能和湍流耗散率采用二阶迎风格式,亚松弛因子均采用默认值。

通过仿真可获得减速伞不同开伞角度、不同运动速度条件下的大量仿真结果,这里仅给出部分仿真结果,如图4所示。

图4 运动速度为6 m/s时不同开伞角度下的流场压力云图

2.4 分离阶段的数学模型

在武器到达分离深度时,两舱段分离开始后,减速伞关闭。此时,连接两舱段之间的钢缆是影响两舱段运动的主要因素。经推导,武器舱与压载舱的运动方程如下。

①武器舱。

(6)

②压载舱。

(7)

根据方程(6)、方程(7),可解得任一时刻的加速度,则运动坐标系下的任一时刻两舱段的速度为

(8)

同理可通过坐标转换求得武器舱和压载舱在固定坐标系下的速度与位置。

武器舱和压载舱之间的钢缆作用力Fd根据分离情况不同可分别按以下方法求取。

①钢缆拉直前的阶段。

在武器刚分离直至钢缆拉直时,作用在武器舱和压载舱之间的钢缆作用力可按下面方法计算。

钢缆受力情况如图5所示,拉直中的钢缆微元质量dmp可写成如下的动量方程:

vRdmp=(Fd-FR)dt

(9)

(10)

式中:vR为钢缆微原质量拉出速度;FR为钢缆的拉出阻力;l为钢缆拉出长度;v1,v2分别为武器舱和压载舱在固定坐标系中的速度。

图5 钢缆的受力分析

式(9)可改写成:

(11)

②钢缆拉直后的阶段。

当武器的2个舱体分离距离大于钢缆最大长度时,钢缆将拉直。此时作用在武器舱和压载舱的钢缆作用力可根据动能守恒和动量守恒定律进行计算。

计算中假设:钢缆在拉伸过程(见图6)中无能量损失,钢缆的弹性模数E为常数,并忽略武器由于势能变化而引起的动能变化,则根据能量守恒定律,在此过程中,武器系统的动能变化应等于海水阻力和钢缆张力分别对武器舱和压载舱所做的功之和,即

(12)

式中:m1,m2分别为武器舱和压载舱的质量;v为钢缆伸长到最大时的整个武器速度;FD1,FD2分别为武器舱、压载舱的阻力;s1,s2分别为武器舱、压载舱在钢缆拉直到伸长最大时所经过的距离。

图6 钢缆拉伸过程示意图

为了简化式(12),参数取平均值:

(13)

(14)

(15)

(16)

(17)

s2-s1=lεmax

(18)

式中:εmax为钢缆的最大变形量;Cx1,Cx2分别为武器舱和压载舱的流体阻力系数,td为钢缆拉伸过程的时间。

将式(16)、式(17)代入式(18),得:

(19)

则式(12)简化为

(20)

当钢缆拉直后,武器整体速度v既不等于v1也不等于v2,其大小与武器质量之比有关。假设质量之比为

当忽略海水阻力的能量损失时,武器整体拉直前后的动量守恒式为

m1v1+m2v2=(m1+m2)v

(21)

化简为

m2v2-m2v=m1v-m1v1+m2v1-m2v1
m2(v2-v1)+(m1+m2)v1=(m1+m2)v

则有

v=KmvR+v1

(22)

将式(22)代入式(20),得:

(23)

令:

A=E,

B={(KmvR+2v1)FD1+[(Km+1)vR+2v1]FD2}/vR,

则

(24)

(25)

根据以上方法即可获得钢缆拉直后产生的拉力Fd。

3 仿真结果及分析

主要仿真参数为:武器开伞前初速度u=6 m/s;武器初始负浮力FW-FB=98 kN;武器的重心、浮心坐标:Gc(0.4,0),Bc(-0.2,0);连接2个舱段之间的钢缆最大长度为10 m。

3.1 仿真结果

通过仿真可获得武器采用不同减速伞开启角度(这里指开伞后最终稳定张开的角度)时的减速效果。2个舱段在不同情况(如不同开伞深度、不同分离开始深度、不同开伞角度以及不同钢缆长度等)下的仿真结果如图7所示。由于篇幅原因,下面仅给出在以上仿真条件下3种情况的仿真结果。

①减速伞开启角度为10°,减速伞开启深度为2 950 m,分离深度为2 990 m时的仿真结果如图8所示。

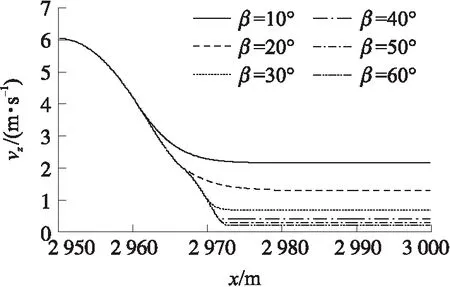
图7 不同减速伞开启角度β时,武器开伞后的纵平面速度随深度变化曲线

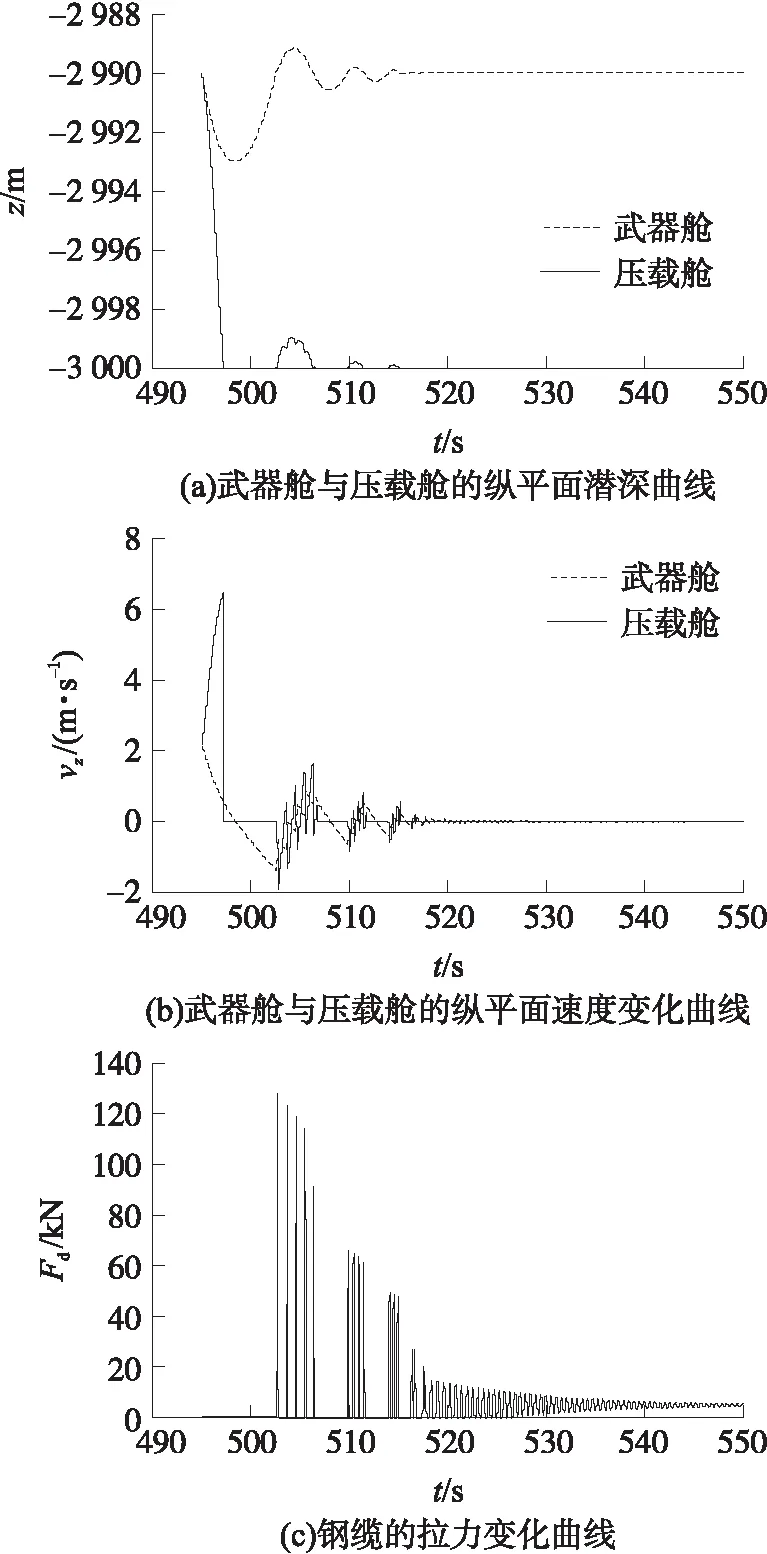
图8 减速伞开启角度为10°时的仿真结果

②减速伞开启角度为30°,减速伞开启深度为2 950 m,分离深度为2 990 m时的仿真结果如图9所示。

图9 减速伞开启角度30°、开启深度2 950 m时仿真结果

③减速伞稳定开启角度为30°,减速伞开启深度为2 970 m,分离深度为2 990 m时的仿真结果如图10所示。

3.2 仿真结果分析

从仿真结果可见:

①武器采用减速伞的减速效果十分明显,在减速伞稳定开启角度为10°条件下,武器的运动速度就由6 m/s降低到2.2 m/s,期间武器模块下沉了33 m左右(见图7)。随着减速伞最大开启角度的增加,武器模块减速效果增大,在减速伞开启角度依次为10°,20°,30°,40°,50°,60°时,武器模块减速后的稳定速度依次为2.2 m/s,1.3 m/s,0.67 m/s,0.4 m/s,0.28 m/s和0.22 m/s(见图7)。

②当减速伞开启角度较小时(如10°),压载舱在分离时初始速度较大(分离时压载舱下沉速度为2.2 m/s,见图8(b)),此后压载舱将加速下沉并以较大速度到达海底(压载舱到达海底时速度为6.5 m/s)。而武器舱在分离后则在正浮力的作用下,先减速下沉,后加速上浮。在钢缆拉直前,武器舱的速度为-1.4 m/s(见图8(b)),此时钢缆对两舱的作用力为128 kN(见图8(c))。因钢缆的作用一方面会减小武器舱上浮速度,另一方面当作用力大于压载舱负浮力时则会将压载舱从海底拉起。以上过程将如此反复直至武器舱稳定悬浮在海底(见图8(a))。

图10 减速伞开启角度30°、开启深度2 970 m时仿真结果

③当减速伞开启角度较大时(如30°),在武器分离时,武器舱及压载舱初始速度较小,武器舱因正浮力作用上浮过程相对较长,因此在压载舱到达海底前,钢缆已拉伸到最大长度,此时钢缆的作用力分别使武器舱向下和压载舱向上运动(见图9(a))。当减速伞开启角度较大时,则武器舱及压载舱分离时的初始速度越小,相应地,在钢缆拉直瞬间,武器舱获得的上浮速度越大(武器舱上浮速度为0.54 m/s,见图9(b)),则钢缆拉直瞬间对2个舱段产生的拉力为308 kN(见图9(c))。

④在同样的减速伞开启角度下,改变减速伞开启深度,可有效减小钢缆作用力,减少着陆过程的震荡。以减速伞开启角度30°为例,当分离深度同为2 990 m时,如减速伞开启深度为2 950 m,钢缆最大作用力为308 kN(见图9(c)),而将减速伞开伞深度改为2 970 m,钢缆的最大作用力仅为61 kN(见图10(c)),而且着陆后震荡后者小于前者(见图9(a)和图10(a))。

4 结论

为了研究潜伏式武器使用减速伞减速及舱段分离方法实现水下安全着陆的可行性,建立了相关运动数学模型,并开展着陆运动过程的仿真研究。仿真结果表明:①武器采用不同的减速伞开启角度可获得不同的减速效果,开启角度越大,减速效果越好;②使用减速伞加舱段分离的方法可保证武器安全着陆。这种方案的减速着陆效果与减速伞开启角度、开启深度、分离深度以及钢缆长度参数等密切相关,通过选择合适的参数组合(如减速伞开启角度30°,开启深度2 970 m,分离深度2 990 m,钢缆长度10 m)可以实现武器2个舱段一次安全、稳定着陆,而且在该过程中钢缆受力较小。

在本文的建模及仿真中,未考虑水下涌浪的影响及减速伞开伞过程的动态阻力,后续将开展动态条件及更接近实际状态条件下的武器水下减速着陆仿真,以对其减速着陆的水下运动规律进行更为准确和深入的研究,为后续该武器有关减速着陆部件的设计论证提供理论依据。