大滑滚比条件下非牛顿流体线接触热弹流润滑分析*

唐洪伟1 王 静1 孙楠楠 朱建荣

(1.青岛理工大学机械与汽车工程学院 山东青岛 266520；2.潍柴动力股份有限公司内燃机可靠性国家重点实验室 山东潍坊 261061)

当两表面反向运动，滑滚比S>2时即为大滑滚比工况，广泛见于无保持架轴承、滚珠丝杠、凸轮-平底挺杆副等工业应用中。如果两个表面运动方向相反，而速度大小相等时，则形成了滑滚比为无穷大并且卷吸速度为0的工况，一般称为零卷吸工况。在大滑滚比及零卷吸工况下，热效应起着至关重要的作用，最为典型的就是形成“温度-黏度楔”凹陷[1]，也就是形成凹陷油膜形状并对两接触表面进行保护。杨沛然和常秋英[1]进行了超大滑滚比条件下的线接触热弹性流体动力润滑分析，得到了完全数值，并获得了经典的大凹陷油膜形状。GUO等[2]研究了稳态点接触热弹流润滑问题，并获得了经典的大凹陷形状。YAGI等[3]使用红外测温技术，实验测得了大滑滚比下油膜、球表面及玻璃盘表面温度场分布。零卷吸下，随着两表面滑动速度的增加，接触区内椭圆形凹陷的短轴由与速度方向重合变至垂直于速度方向，中心凹陷深度呈先增大后减小的趋势，凹陷处温度可达400 K，凹陷的形成受“温度-黏度楔”效应的影响。YAGI等[4]后来使用拉曼光谱研究了不同滑滚比下油膜压力分布，发现大滑滚比下出现表面凹陷时，油膜局部压力增加，滑滚比大小影响油膜压力分布。WANG等[5]数值研究了大滑滚比对存在表面波纹度的线接触热弹流润滑的影响，发现表面波纹度的弹性变形、压力和温度的波动随着滑滚比的增加而减小，随着波纹度波长的增加，弹性变形变大。WANG和YANG[6]数值模拟了偏心轮与平底推杆之间的接触并给出了热弹流油膜特性。随后， WU等[7]对凸轮-平底推杆之间的热弹流润滑问题进行了模拟， 并给出了在两反向运动表面速度连续变化过程中热油膜凹陷的变化。ZHANG等[8]通过对线接触零卷吸工况的数值仿真发现，随着两表面速度的降低，经典的大凹陷会演化为接触区中央的小凹陷并最后消失。ZHANG等[9]也对点接触零卷吸工况下低表面速度下的接触区中央小凹陷进行了研究。 张彬彬和王静[10]研究了大滑滚比(滑滚比S小于无穷)热弹流润滑条件下中央小凹陷的变化。

本文作者研究了在大滑滚比条件下，线接触光滑表面非牛顿流体热弹性中央小凹陷的变化以及油膜压力和温度的变化情况。

1 控制方程

文中假设润滑油遵从Ree-Eying流体模型[11]

(1)

式中:u为流体速度;τ0称为Ree-Eying流体的特征剪应力；η称为Ree-Eying流体的表观黏度；τ为流体剪应力。

时变线接触广义Reynolds方程[8]为

(2)

式(2)中使用的当量参数定义为

式中:p为流体压力；h为油膜厚度；t为时间变量。

式(2)的边界条件为

(3)

载荷方程为

(4)

膜厚方程为

(5)

式中:变量h00由载荷方程(4)决定。

密度-压力-温度关系[8]为

(6)

式中:ρ0为润滑油的环境密度;T0为环境温度。

黏度-压力-温度关系采用Roelands关系式[12]

η=η0exp{A1[1+(1+A2p)Z(A3T-A4)-S]}

(7)

(8)

忽略热辐射和在X、Y方向上的热传导，那么油膜能量方程可写为

(9)

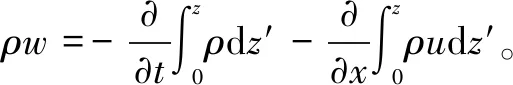
油膜能量方程[9]的边界条件为

(10)

两固体能量方程为

(11)

式中:ca、cb分别为固体a和b的比热容；ρa、ρb分别为固体a和b的密度；ka、kb分别为固体a和固体b热传导系数。

两固体的边界条件如下：

(12)

在两个固-液分界面的热通量连续条件为

(13)

2 数值技术

将上述方程量纲一化，定义如下：

Ua=ua/u0,Ub=ub/u0,U0=η0u0/(E′R),

式中:b为Hertz接触区的半宽度;pH为最大赫兹压力；U0是一个参考速度量，对结果不产生影响，文中U0=1×10-11。

Reynolds方程使用多重网格技术求解，弹性变形使用多重网格积分法[13]计算。多重网格结构由7层网格组成，顶层网格节点数为1921。温度计算在最顶层网格上进行，使用逐列扫描技术。在油膜厚度方向布置21个等距节点，固体a和固体b内沿Za和Zb方向各布置12个不等距节点。在结果分析中使用演示结果的量纲一膜厚H=(h/R)×105。

3 结果和讨论

采用钢-钢接触，主要参数为：环境黏度η0=0.08 Pa·s，黏压系数α=2.210m2/N,环境密度ρ0=875 kg/m3，润滑油的比热容c=2 000J/(kg·K),热传导系数k=0.14 W/(m·K)；两固体密度ρa,b=7 850 kg/m3，两固体比热容ca,b=470 J/(kg·K)，两固体的热传导系数ka,b=46 W/(m·K)，G=5环境温度T0=313 K，U0=110。计算边界3.0≤X≤3.0。滑滚比定义为S=2.0(uaub)/(ua+ub)。施加的量纲一载荷W=810(pH=0.811 GPa)，设定固体a表面的3个量纲一速度Ua分别为0.22、0.44和0.77。

图1所示为固体a表面速度Ua为0.22，固体b表面速度Ub分别为-0.055、-0.11和-0.22时的压力和膜厚分布。图2给出了3种工况所对应的两固体表面及油膜中最大温度所在油层的温度分布曲线。

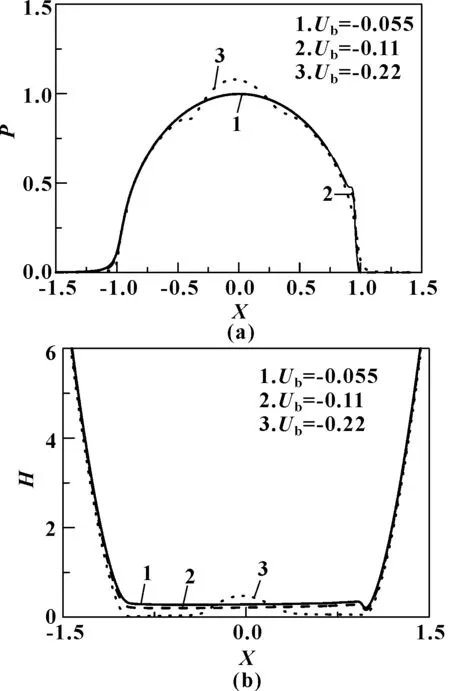
图1 低速条件下油膜压力和膜厚分布(Ua=0.22)

图2 低速条件下两固体表面及油膜中最大温升所在油层的温度曲线分布

如图1所示，当Ub分别为-0.055和-0.11时，油膜中没有凹陷产生，压力分布中也没有凸起。对应的油膜温度分布曲线显示，Ub从-0.055变化为-0.11时，油膜温度略有升高,如图2(a)、(b)所示。如图1所示，当Ub=-0.22时，压力曲线中央出现一个凸起，对应的膜厚曲线中心位置出现一个浅的凹陷，而此凹陷两侧的膜厚则明显降低。说明在低速条件下，零卷吸工况更不利于润滑。对应的图2(c)中，油膜温度总体上比图2(b)升高，但是与油膜凹陷对应的位置处，两固体表面上的温度曲线有轻微下降，而油膜中最大温升Tmax曲线在该位置升高。

图3所示为固体a表面速度Ua为0.44，固体b表面速度Ub分别为-0.11、-0.22、-0.28、-0.33、-0.35及-0.44时的压力和膜厚分布。图4给出了6种工况所对应的两固体表面及油膜中最大温度所在油层的温度分布曲线。如图3所示，Ub分别为-0.11和-0.22时在接触区右侧压力有轻微凸起，对应位置处膜厚有小凹陷产生；Ub为-0.28时，靠近X=1.0左侧压力有一明显凸起，膜厚曲线有一明显小凹陷出现。此后，Ub的反向增加，压力的凸起及油膜的凹陷逐渐向接触中心位置移动。在Ua=-Ub=0.44时即零卷吸工况下，压力凸起和油膜凹陷都位于接触区中央。但需要指出，Ua=-Ub=0.44时的油膜凹陷深度小于Ua=0.44、Ub=-0.33和-0.35条件下的凹陷深度。并且当Ua=-Ub=0.44时，油膜凹陷两侧的膜厚有明显降低。在图4(a)、(b)中，油膜温度无明显变化，从图4(c)中Ub=-0.28开始，在X=1.0左侧温度曲线有微小凸起，此后随着Ub的反向增加，该凸起高度增加并且向中央位置移动，最后处于接触区中央位置。表面b的温升曲线在0≤X≤1.0范围内也是处于逐渐增加过程的。

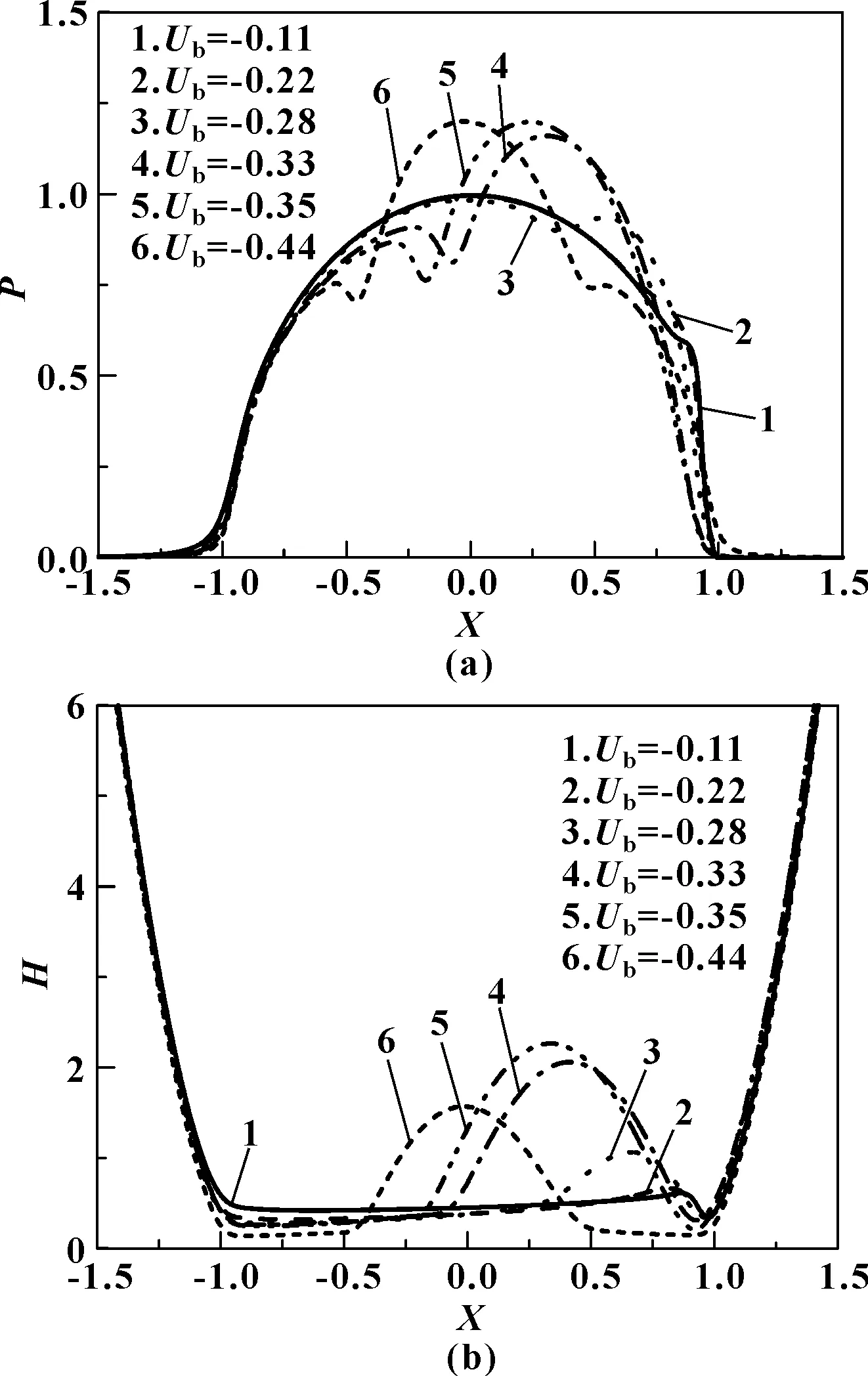
图3 中速条件下油膜压力和膜厚分布(Ua=0.44)

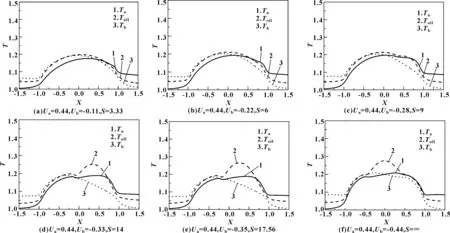
图4 中速条件下两固体表面及油膜中最大温升所在油层的温度曲线分布

图5所示为固体a表面速度Ua为0.77，固体b表面速度Ub从-0.11变化到-0.77范围内的油膜压力和膜厚分布。图6给出了9种工况所对应的两固体表面及油膜中最大温度所在油层的温度分布曲线。如图5所示，当Ub分别为-0.11和-0.22时压力曲线仅在X=1.0附近有轻微凸起，对应位置膜厚有较浅凹陷产生；Ub为-0.33时在出口区出现明显压力凸起，对应的膜厚位置处有一个明显的小凹陷产生。此后，Ub的反向增加，压力的凸起及油膜的凹陷逐渐向接触中心位置移动。在Ua=-Ub=0.77时，压力凸起和油膜凹陷都位于接触区中央。此时所形成的凹陷为经典的大凹陷，与图3中所示的中央小凹陷不同。从图6中可见到与图4相似的温度曲线变化趋势，只是温升更高。

文中的表面凹陷现象也是“温度-黏度楔”[1]作用的结果。

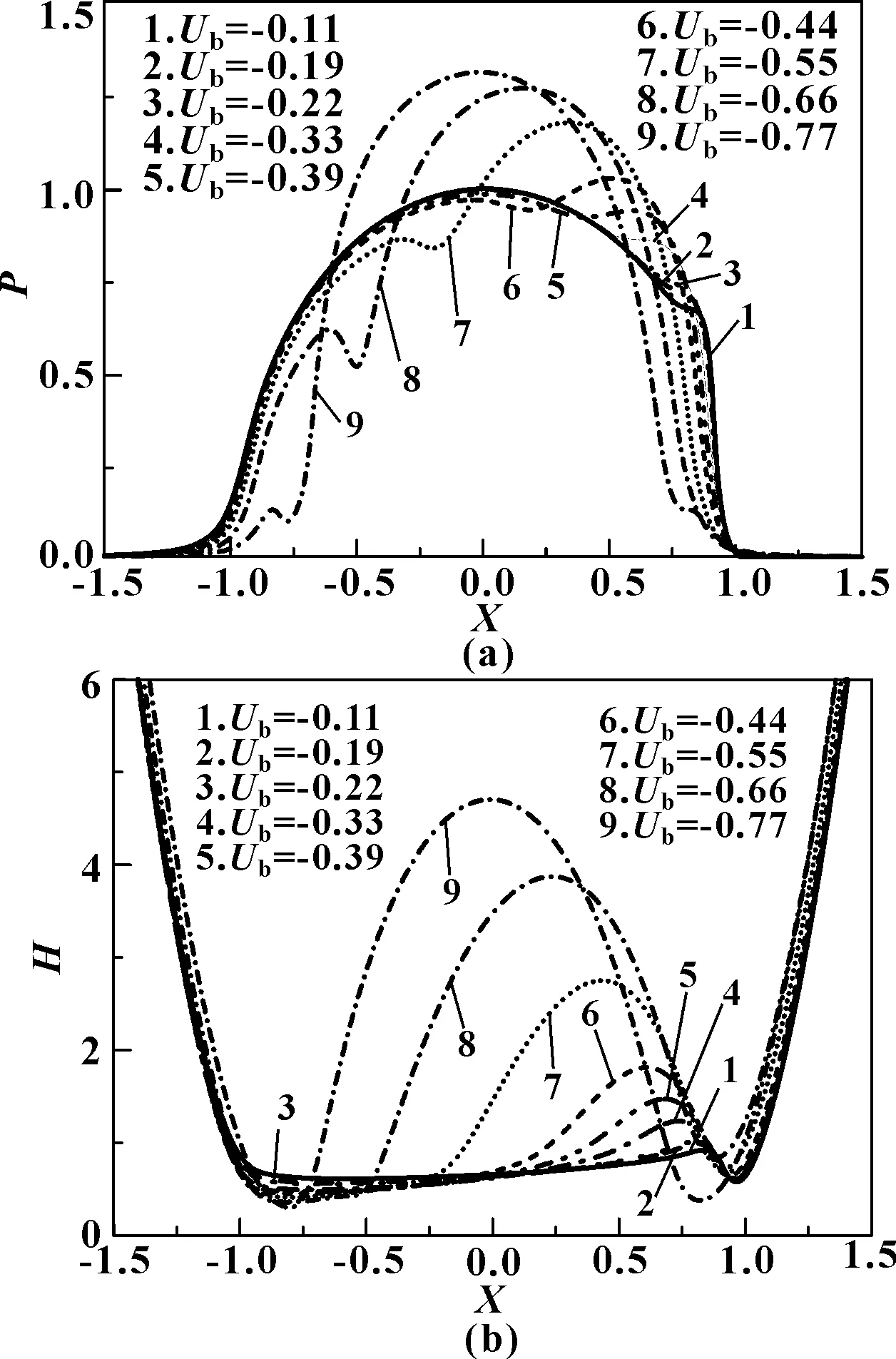
图5 高速条件下油膜压力和膜厚分布(Ua=0.77)

图6 高速条件下两固体表面及油膜中最大温升所在油层的温度曲线分布

4 结论

(1)当表面速度增大时，“温度-黏度楔”效应增强，随着滑滚比的增大，压力峰、油膜凹陷朝中心接触区移动，压力峰变大，中心凹陷加深。

(2)随着滑滚比的增加，较高速度的油膜温度比低速度油膜温度高，且随着滑滚比的增加油膜温度增加较快，零卷吸工况下，接触区中心的温度峰值比固体表面温度高很多，而较低速度的油膜温度与固体表面温度相差不大。