空间碎片清除轻气炮内弹道参数优化选择

安继萍，李新洪，张治彬

(航天工程大学 宇航科学与技术系，北京 101416)

轻气炮作为高速弹丸发射装置被普遍运用在高压作用下的材料动态响应特性分析、激波传感器的标定、空间碎片对航天器防护结构的撞击效果实验以及动能武器的研究中[1-3]。同时，将轻气炮作为航天器有效载荷，进行空间碎片清除的设想也为轻气炮扩展了任务空间[4]。

内弹道参数的设计是进行轻气炮结构设计的基础，也是评估轻气炮任务能力的关键。不同任务的轻气炮的内弹道参数设计，多利用轻气炮内弹道方程，根据不同的设计需求进行气室容积、气室初始压力、炮管口径以及炮管长度、驱动气体参数等内弹道参数的确定[5]。相较于地面安装的轻气炮，空间碎片清除轻气炮的特殊任务需求、部署环境与高昂的设计成本，为其内弹道参数提出了更多的设计约束。

笔者针对空间碎片清除轻气炮的特殊设计需求，以轻气炮炮身质量和弹丸炮口速度为设计约束，利用内弹道方程和AMEsim数值仿真进行内弹道参数的优化选择。

1 空间碎片清除轻气炮的设计需求

1.1 轻气炮的工作原理

空间碎片清除轻气炮利用储存气体的高压气瓶向排气腔充气，高压气体推动锥形阀封闭炮管口，打开单向阀并将气室充气至预定压强。弹丸发射时排气腔向外排气，锥形阀在压差的作用下打开炮管口，高压气体进入炮管推动炮管内的弹丸高速发射，空间碎片清除轻气炮的结构示意图如图1所示。

1.2 设计目标

轻气炮的内弹道参数主要包括：炮管口径、气室压强、气室容积、气体种类以及炮管长度。以天基远距离清除1～10 cm量级空间碎片目标为基础，炮管口径选择较为适中的20 mm，该口径下设计的柱形弹丸质量5 g.

在清除空间碎片的任务中，弹丸质量与弹速是决定航天器碎片清除能力的关键。该任务需求下设定的弹速为1 200 m/s[4].为实现该设计目标，需要进行气室容积V，气室初始压强p，炮管口径d，炮管长度l，气体种类等内弹道参数的优化选择。

在达到预定弹丸炮口速度同时，内弹道参数的选择对弹丸膛内发射时间和轻气炮炮身质量两设计指标也会产生重要影响，所以在轻气炮设计过程中以预定弹速为设计目标的同时，需要以轻气炮炮身质量和弹丸膛内发射时间为设计约束进行参数选择。

2 气体种类与气室容积选择

2.1 内弹道方程

气体炮的发射能力是设计气体炮的重要指标，也是实验工作者比较关注的重要指标之一，但是某一发射速度下各内弹道参数可以有多种组合，各参数与弹速的关系利用轻气炮内弹道方程进行描述[6-8]，该方程基于3种假设：

1)气室气体为理想气体，整个发射过程视为理想气体绝热膨胀过程。

2)不考虑弹前气体压力的影响。

3)不考虑各种损耗的具体形式，在计算过程中引入次要功系数φ来计入能量损失因素。

根据以上假设与严密推导，得到了轻气炮内弹道方程:

(1)

(2)

式中：v为弹丸炮口速度；S为炮口截面积；md为弹丸质量；γ为气体绝热系数(单原子气体一般为1.44)；φ为次要功系数；K为摩擦损耗系数；mg为每发气体的质量。

2.2 气体种类选择

轻气炮弹丸驱动气体需要较好的弹丸驱动能力，由内弹道方程可知轻气炮的弹速随着驱动气体的分子量的减小而增大[9]，所以氦气和氢气是较为理想的驱动气体，而氦气因为是惰性气体，安全性高，是较为适宜的空间碎片清除轻气炮驱动气体。

2.3 气室容积选择

轻气炮内弹道方程中气室容积与弹丸炮口速度不是单调关系，通常会存在一个最佳的气室容积，在一定弹丸炮口速度下，最佳气室容积也受气室压强、炮管长度的影响，但相同炮管长度下最佳气室容积不变，以1.6 m炮管长度下弹丸炮口速度随着气室容积的关系曲线为例，如图2所示，可知最佳气室容积在1.0 L左右。

通过计算不同炮管长度下的气室容积与弹丸发射速度关系，发现在1 200 m/s的弹速目标下最佳气室容积集中在0.8～1.2 L，笔者选择气室容积0.9 L进行轻气炮设计。

3 气室压强与炮管长度优化

3.1 评价指标确定

在航天器的设计中，实现最小质量的工程和制造费用，减轻航天器的发射质量有很大的经济效益。轻气炮气室容积与炮管长度是影响气体炮质量的关键参数，气室压强增加，气体炮结构的壁厚相应增加；炮管长度增加，轻气炮质量也增加。

同时轻气炮气室容积与炮管长度也是影响弹丸膛内发射时间的关键参数，弹丸膛内发射时间即下达发射指令后弹丸飞出炮管的时间，对于空间碎片清除轻气炮来说，在执行空间碎片清除任务过程中，弹丸膛内发射时间是决定任务成功率的主要指标，轻气炮弹丸膛内发射时间短，天基平台姿态调整幅度小，解算时间短，瞄准精度高，将大大提高任务成功率，从而带来巨大的经济效益。

综上，在实现1 200 m/s的弹丸炮口速度、保证结构强度的情况下，笔者综合利用轻气炮炮身质量和弹丸膛内发射时间2个评价指标进行气室压强和炮管长度的优化。

3.2 质量预估

在轻气炮的详细机械结构未知的情况下进行质量预估，目的是反映轻气炮炮身质量与气室压强和炮管长度的关系。根据气室的直径一般为炮管口径的4～5倍的设计原则[8]，取气室直径为80 mm，相应的圆柱状的气室长度为19.9 cm.锥形阀的设计半径20 mm，长度70 mm.利用管道应力分析公式进行壁厚计算[10]:

k=(d+2h)/d,

(3)

(4)

式中：h为壁厚；σmax为轻气炮材料强度极限，轻气炮炮身材料铝合金的极限强度为523 MPa；k为直径比。

计算壁厚时利用强度极限与气室压强的关系求解k值，再利用k反解出不同压强下需要的结构壁厚。轻气炮炮身质量m是气室质量ms与炮管质量mp之和，其质量估算公式为

mp=3.14ρ[(10+h1)2-102]l,

(5)

ms=3.14ρ[(40+h2)2-402]l2+

3.14ρ(40+2h2)2h2+3.14ρ(20+2h2)2l3,

(6)

式中：l为炮管长度；l2为气室长度；l3为锥形阀长度；h1为炮管壁厚；h2为气室与锥形阀壁厚；ρ为铝合金密度。

在1 200 m/s的发射速度下，通过计算不同气室压强下的炮管长度与轻气炮质量，绘制其关系如图3所示。

从图3可以看出，在1 200 m/s的弹丸炮口速度下，随着气室压强的增加，炮管长度不断减小，炮身质量在气室压强为6 MPa时出现最小值，此时的炮管长度为6.78 m.随后轻气炮炮身质量随着气室压强的增大而急剧增大。

虽然以轻气炮炮身质量进行评价时可得到最佳气室压强，但考虑到空间碎片清除轻气炮天基部署的特点，此最佳气室压强下炮管过长，不易进行姿态控制，且给轻气炮的安装固定带来困难，同时，炮管长度过大，导致弹丸膛内发射时间过长，所以，需要利用第2个评价指标，即弹丸膛内发射时间进行轻气炮的炮管长度与气室压强的选择。

3.3 弹丸膛内发射时间预估

弹丸弹丸膛内发射时间同样可以利用轻气炮的内弹道方程进行计算，但是内弹道方程推导过程是基于弹底压力的均匀性假设，没有考虑轻气炮气室内气体的波动、锥形阀的发射延迟等影响因素，对于弹丸膛内发射时间的计算准确性较低。现利用AMEsim仿真软件建立轻气炮的模型，在考虑弹丸与轻气炮炮身的摩擦，锥形阀的开启延迟、气体的波动等因素的情况下，对弹丸膛内发射时间进行更精确的仿真计算。建立的AMEsim模型如图4所示。

AMEsim模型中利用Pneumatic Component Design 库中的活塞元件、气动压力源元件以及质量元件模拟排气腔向外排气以及锥形阀发射过程，利用pneumatic volume元件分析各个腔室的体积与气压变化。仿真时对各元件的参数进行设定，改变气室压强，在炮管长度未定的情况下选择弹丸位移达到2 m时所用的时间t作为第2个评价指标，记录数据如表1所示。

表1 不同压强下的弹丸膛内发射时间

3.4 评价方程

根据压强与弹丸炮口速度成正比关系，确定压强p与弹丸膛内发射时间t成反比，利用公式(7)表示压强与弹丸膛内发射时间的关系:

(7)

式中，a、b、c为常数。

对表1中的数据进行拟合，得到实际曲线与拟合曲线，如图5所示。拟合得到a=31.63,b=4.03,c=0.98，拟合曲线与实际曲线的重合度较好。

对压强p和轻气炮预估质量m的关系曲线进行二次曲线的拟合，拟合得到的两条曲线如图6所示。

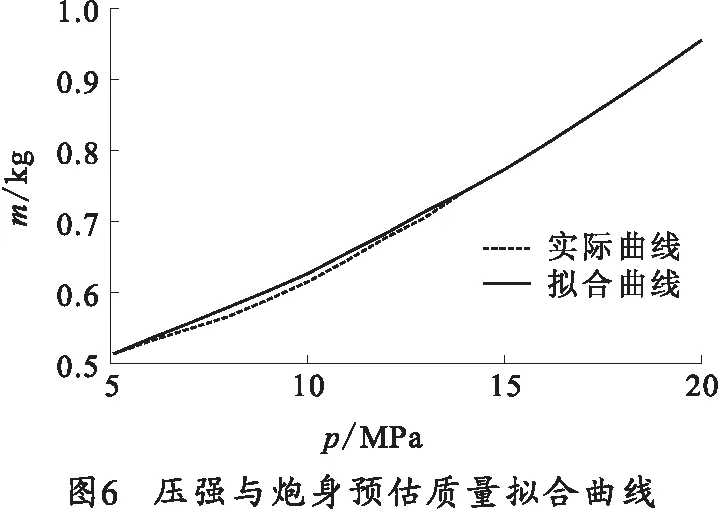
轻气炮预估质量的拟合曲线的方程为

m=0.64p2+13.3p+430.1.

(8)

将两个拟合方程无量纲化，利用与权重系数相乘得到评价方程:

f(p)=k1t/ta+k2m/ma,

(9)

式中：k1，k2分别是弹丸膛内发射时间和质量的权重系数；ta和ma分别是压强由5 MPa提至30 MPa弹丸膛内发射时间和质量的变化量。

将式(7)、(8)带入方程(9)得到的评价方程：

f(p)=k1[3.16/(p+4.03)+0.98]/2.7+

k2(0.64p2+13.3p+430.1)/802.3.

(10)

确定权重系数的比值k1/k2，即比较弹丸膛内发射时间缩短1 ms与轻气炮炮身质量减轻1 g所带来的设计效益的关系，是确定评价方程的关键。

3.5 评价方程分析

对于航天器来说，减小航天器质量可以大幅节约发射成本，例如利用最常用的“西方世界”的一次性运载工具向地球同步转移轨道发射质量为1 kg的航天器的费用大约是25 000美元[11]。轻气炮的气室压强的减小可以很大程度地减小轻气炮的壁厚，从而减小航天器质量，但是在减小压强的同时也造成弹丸膛内发射时间的增长,会大幅削减航天器执行任务的能力，造成航天器整体效益下降。所以权重系数的确定需要考虑到整个航天器设计制造的成本、航天器任务价值以及弹丸膛内发射时间对于该价值实现的影响程度的大小，这是一个复杂的系统工程，需要进行大量的计算评估，在经济效益标准、生产制造标准、研制时间标准等不同标准下，选择的权重系数也不同。

笔者不对权重系数的确定过程作详细说明，仅选择几组典型权重系数的比值，将其代入优化方程，绘制压强曲线图，如图7所示。在不同权重系数下进行压强与炮管长度的选择说明。

由图7可知，进行压强与炮管长度的优化，可以遵循以下几条原则：

1)当质量效益远大于弹丸膛内发射时间效益时，在安装条件允许的情况下，可以选择小的气室压强。当权重系数比值为0.3时，最佳气室压强将接近0.

2)当质量效益小于发射效益，且两者权重系数比值系数在0.3到50之间时，可以根据评价方程选择一个最佳气室压强。例如，当选择权重系数比值为10时，即确定的最佳气室压强为15 MPa，炮管长度为1.56 m.

3)当质量效益远小于发射效益时，在气瓶充气条件允许的情况下，可以尽可能选择较大的气室压强。当权重系数比值大于50，最佳气室压强将超过气瓶的最大可供气压强30 MPa.所以，当权重系数比值大于50时，气室压强只能选择在气瓶供气条件允许的情况下的最大气室压强。

4)一般情况下，弹丸膛内发射时间缩短带来的经济效益会远大于质量减少，所以气室压强的选择最终的限制条件是气瓶的供气特性，即气瓶的合理设计是影响轻气炮设计的重要因素。

4 结束语

不同任务需求的轻气炮的结构参数设计需要遵循不同的设计约束，天基轻气炮的设计需要根据特殊的任务环境进行设计参数的选择。笔者利用轻气炮的内弹道方程选择了气室容积和驱动气体。选择轻气炮质量和弹丸膛内发射时间作为评价指标，利用内弹道方程和AMEsim模型建立每个指标与压强和炮管长度的方程，分析了两方程在不同权重系数的关系下炮管长度与气室压强的选择原则，为天基轻气炮的参数设计提供了一种系统的选择方法，对天基轻气炮的设计有着很大的借鉴作用。