基于非滑动式与滑动式BDS精密星历内插及其精度分析
从建锋,刘智敏,2,刘 盼,郭金运
(1.山东科技大学 测绘科学与工程学院,山东 青岛 266590;2.山东省基础地理信息与数字化技术实验室,山东 青岛 266590)
北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)采用混合星座组成,包含地球静止轨道卫星(GEO)、倾斜地球同步轨道卫星(IGSO)、中地球轨道卫星(MEO)[1]。BDS在高精度定位的过程中,需要数据分析中心提供高精度精密星历获取卫星三维位置坐标,但其采样间隔为15min,而接收机的采样间隔一般为30s、10s、5s或1s,因此,如何获取任意历元BDS卫星位置成为一个重要问题[2-4]。得到任意历元BDS卫星三维坐标就必须对精密星历进行高精度内插[5-8]。插值法具有过程简便、高效等优点,插值法的基本思想是由很多个已知离散自变量以及对应的因变量值组成某一近似多项式函数,可插值出任意离散点的变量值[9]。目前对卫星精密星历进行插值方法有很多,主要有Lagrange插值方法、 Newton插值方法、Chebyshev插值方法、三次样条插值方法等。文献[2]采用拉格朗日和切比雪夫多项式实现对GPS精密星历内插;文献[3]采用滑动式Lagrange插值方法实现对GPS精密星历进行内插;文献[5]和[6]对实现GPS精密星历内插不同方法进行比较分析。Lagrange插值方法是经典的插值方法,但是常规Lagrange插值方法在插值两端易产生“龙格”现象,为进一步提高Lagrange插值方法在BDS精密星历内插中的精度,需对比非滑动式与滑动式Lagrange插值方法对BDS精密星历内插的影响。BDS与GPS相比,有3种不同类型卫星,对BDS精密星历内插必须考虑到不同类型卫星与插值阶数的关系。本文基于非滑动式与滑动式Lagrange插值方法对BDS精密星历进行内插,借助武汉大学IGS数据中心提供的采样间隔为15 min的BDS精密星历数据,用非滑动式与滑动式Lagrange插值方法分别对BDS精密星历进行内插,结果表明,滑动式Lagrange插值方法精度明显优于非滑动式Lagrange插值方法。
1 两种插值数学模型
1.1 Lagrange插值数学模型
假设y=f(xi)在区间[a,b]上是个实函数,xi是区间[a,b]上n个互异实数,且函数y=f(xi)在区间[a,b]上n+1阶可导,那么在区间[a,b]上任意一点x的n阶Lagrange插值多项式代数表达式为[10]
(1)
对BDS精密星历进行n阶Lagrange内插,可以获取任意历元BDS卫星位置坐标。选择某一时刻t作为插值点,并且在进行插值的区间中满足:插值节点数≥插值阶数+1[11]。在插值时选择一个区间[t0,t1],将t作为自变量,利用式(1)分别求出任意时刻卫星X,Y和Z方向的坐标分量,从而得到任意历元卫星的位置。任意历元卫星位置表示为
(2)
式中:i≠j,Xt,Yt,Zt是t时刻卫星位置三维坐标分量。该方法数学模型简单,是经典的插值方法,采用MATLAB语言编程实现。
1.2 滑动式Lagrange插值数学模型
滑动式Lagrange插值方法是使用Lagrange插值数学模型的基础上不断改变插值区间,使待插值点一直保持在插值区间的中间点上,以此来提高插值的精度。对BDS精密星历进行n阶Lagrange内插,当n为偶数时,生成n-1(奇数)阶插值多项式,如选择16个插值节点,可以生成15阶插值多项式,此时求得的插值结果只保留第8和第9插值节点中间的插值结果;当n为奇数时,生成n-1(偶数)阶插值多项式,如选择15个插值节点,可以生成14阶插值多项式,此时求得的插值结果只保留第7和第8、第8和第9插值节点中间的插值结果。滑动式Lagrange插值可以抑制插值区间两端插值结果的震荡[11],使插值精度达到最优,其插值设计如图1所示。
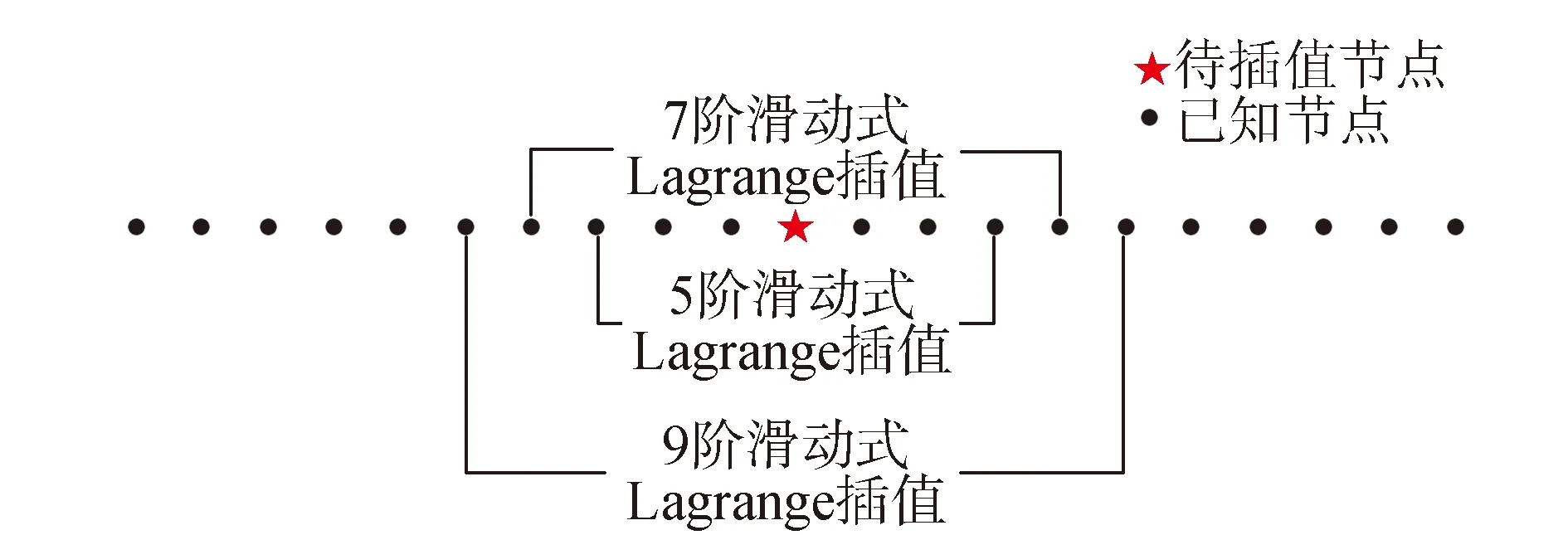
图1 滑动式 Lagrange插值设计
2 实例测试与分析
为了得到任意历元BDS卫星位置坐标,选取由武汉大学IGS数据中心(http://www.igs.gnsswhu.cn)提供的采样间隔为15min精密星历数据,起始历元为2017-06-02 00:00:00,终止历元为2017-06-02 23:30,以每30 min间隔的卫星三维坐标作为已知插值节点,以每15 min间隔的卫星三维坐标作为真值,将计算得到的内插值与真值进行求差得到残差,以残差的均方差根作为插值效果的精度因子。由于BDS包含不同轨道卫星,为了验证插值方法对于不同卫星的影响,采用非滑动式与滑动式Lagrange插值方法分别对北斗GEO、IGSO、MEO 3种不同类型卫星进行内插,分析不同插值方法、不同阶数对卫星类型、插值精度产生的影响,具体操作流程如图2所示[12]。实验中任选PC02(GEO)、PC06(IGSO)、PC12(MEO)3颗卫星进行插值,插值结果如表1、表2和表3所示。
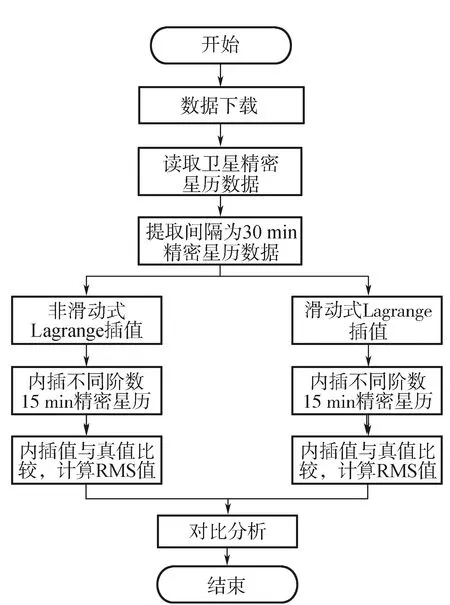
图2 精密星历内插流程
2.1 GEO卫星精密星历内插精度分析
对于非滑动式Lagrange插值方法,从表1和图3中可以看出, GEO卫星的插值精度随着插值阶数的增加而改变。GEO卫星X和Y坐标分量在插值阶数为8阶时插值效果最佳,Z坐标分量在插值阶数为7阶时插值效果最佳。插值阶数在5~7阶变化时,GEO卫星三维坐标分量随着插值阶数的增加RMS值逐渐变小,插值效果逐渐变好;插值阶数在8~20阶变化时,GEO卫星三维坐标分量随着插值阶数的增加RMS值逐渐增大,精度效果逐渐变差。从图4可以看出,对于滑动式Lagrange插值方法,GEO卫星插值精度随着插值阶数的增加,插值效果先逐渐变好,最后趋于稳定。GEO卫星在插值阶数为7~20阶时三维坐标分量的插值精度都能达到亚mm级的精度,且精度效果相当,RMS值趋于稳定。
通过表1数据对比可以看出,非滑动式Lagrange插值方法精度达到最佳时,GEO卫星X,Y,Z坐标分量残差RMS值分别为1.33 mm、0.65 mm、0.61 mm,而滑动式Lagrange插值方法精度最佳时GEO卫星X,Y,Z坐标分量残差RMS分别为0.20 mm、0.23 mm、0.22 mm,插值精度效果有较大幅度的提高。从图5可以看出,GEO卫星9阶滑动式Lagrange插值的残差在区间[-1,1]范围内波动,三维坐标分量插值残差波动幅度相当。
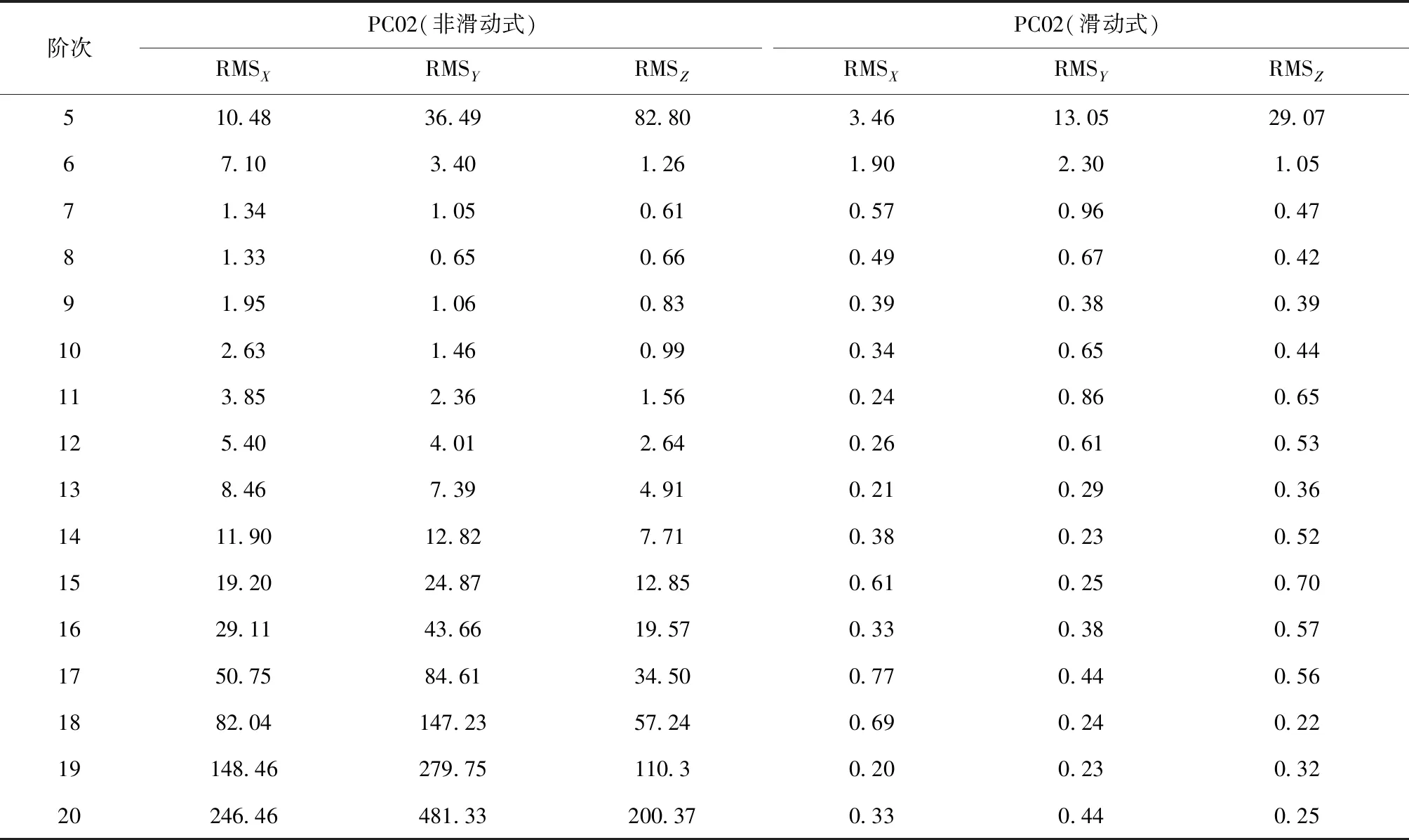
表1 GEO卫星两种方法内插结果 mm
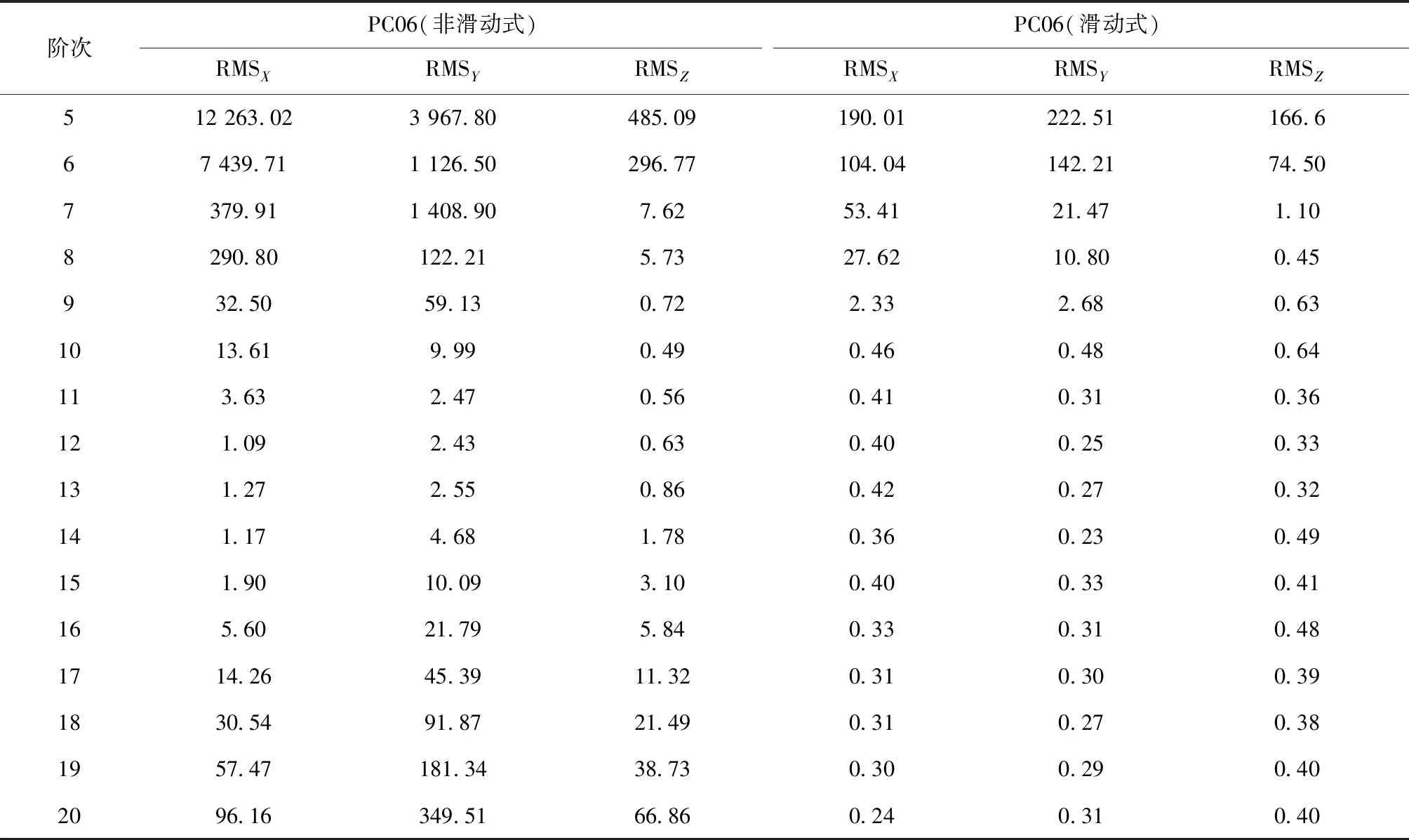
表2 IGSO卫星两种方法内插结果 mm
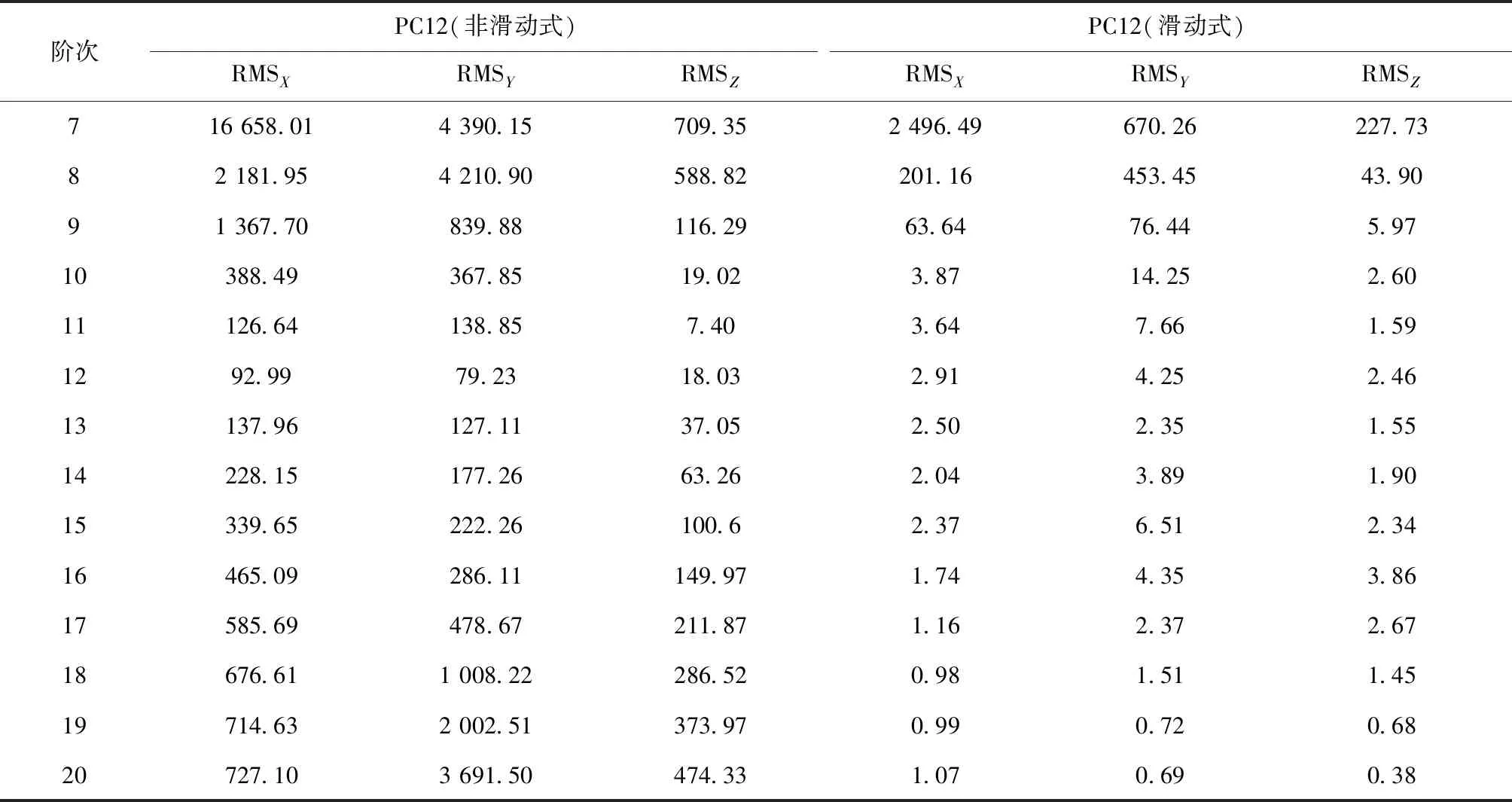
表3 MEO卫星两种方法内插结果 mm
2.2 IGSO卫星精密星历内插精度分析
对于非滑动式Lagrange插值方法,从表2和图6中可以看出, IGSO卫星X坐标分量在插值阶数为11~16阶、Y坐标分量在10~14阶、Z坐标分量在7~16阶时插值精度能达到mm级。X和Y坐标分量在12阶时插值精度最高,Z坐标分量在10阶时插值精度最高。X和Y坐标分量在插值阶数为5~12阶时,随着插值阶数的增加精度效果逐渐提高,在插值阶数为13~20阶时,随着插值阶数的增加精度逐渐降低。Z坐标分量在插值阶数为5~10阶时,随着插值阶数的增加精度逐渐提高,在11~20阶时,随着插值阶数的增加精度逐渐降低。对于滑动式Lagrange插值方法,从图7可以看出,IGSO卫星在插值阶数为9~20阶时三维坐标分量的插值精度能达到mm级,随着插值阶数的增加,RMS值趋于稳定,卫星三维坐标分量插值效果相当。
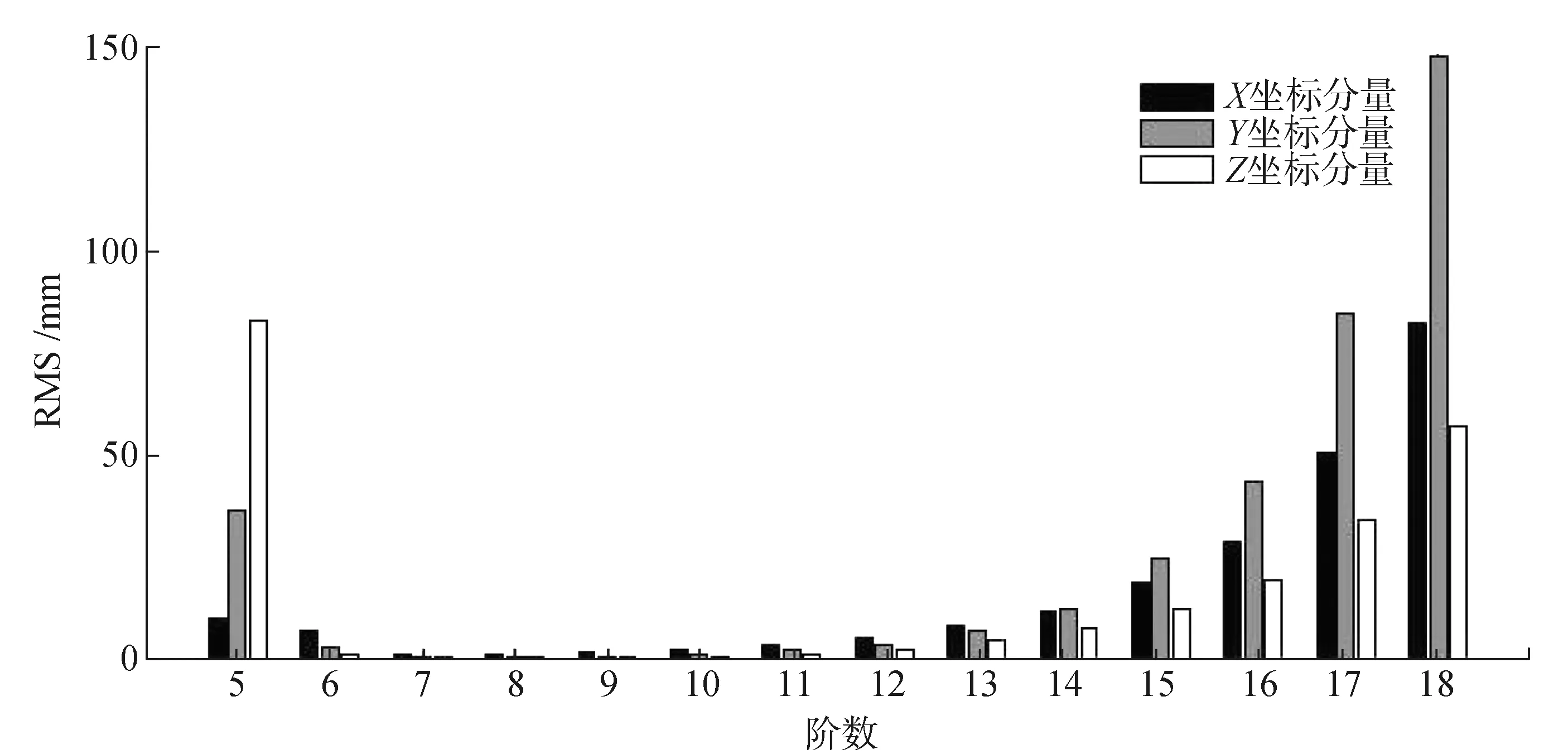
图3 GEO卫星非滑动式插值效果
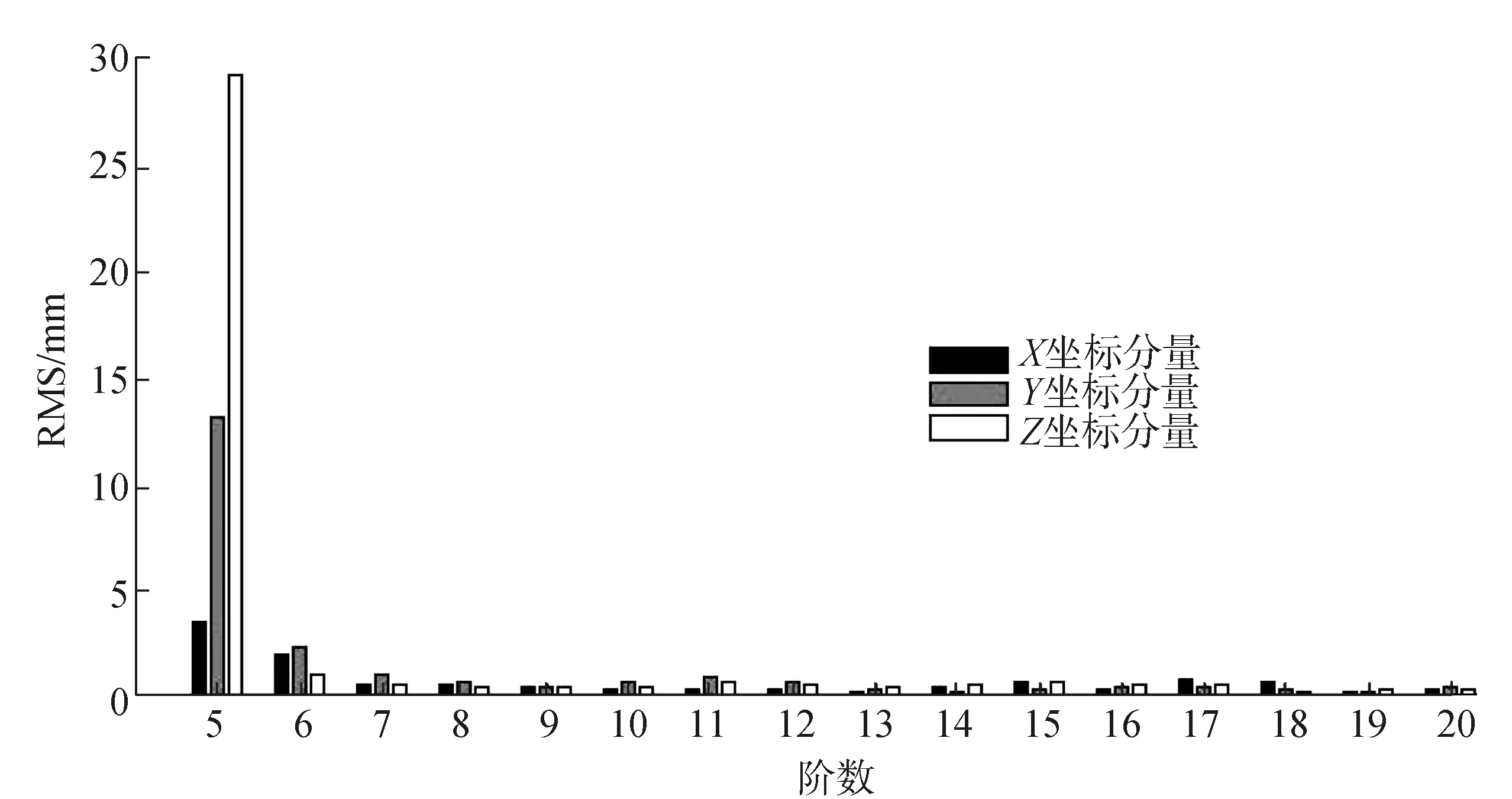
图4 GEO卫星滑动式插值效果
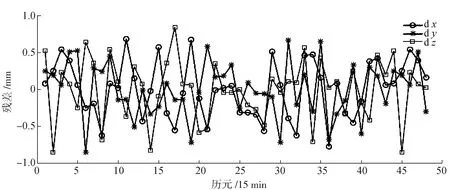
图5 GEO卫星9阶滑动式插值残差分布图
通过表2数据对比可以看出,非滑动式Lagrange插值方法精度达到最佳时,GEO卫星X,Y,Z坐标分量残差RMS值分别为1.09 mm、2.43 mm、0.49 mm,而滑动式Lagrange插值方法精度最佳时GEO卫星X,Y,Z坐标分量残差RMS值分别为0.24 mm、0.25 mm、0.32 mm,插值效果最优时,滑动式效果插值精度更佳。从图8可以看出,IGSO卫星9阶滑动式Lagrange插值的残差在区间[-4,4]范围内波动,三维坐标分量插值残差波动幅度相当。
2.3 MEO卫星精密星历内插精度分析
对于非滑动式Lagrange插值方法,从表3和图9中可以看出,MEO卫星三维坐标插值阶数过低或过高,插值精度效果都较差。MEO卫星X和Y坐标分量只有在插值阶数为12阶时表现出cm级的精度、Z坐标分量在10~14阶表现出cm级精度。在阶数为7~12阶时,MEO卫星X和Y坐标分量随着插值阶数的提高,插值精度效果逐渐变好,在阶数为7~11阶时,MEO卫星Z坐标分量随着插值阶数的提高,插值精度效果变好。在阶数为13~20阶时,随着插值阶数的增加,三维坐标分量插值精度效果都变差。对于滑动式Lagrange插值方法,从图10可以看出,MEO卫星在插值阶数为11~20阶时三维坐标分量的插值精度都能达到mm级的精度。随着插值阶数的增加,三维坐标分量的残差RMS值逐渐变小,最后趋于稳定。
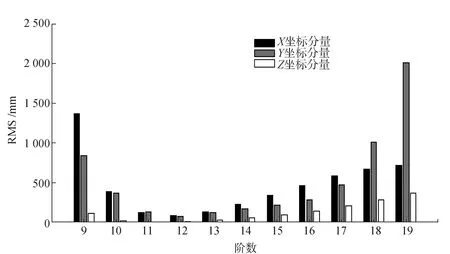
图6 IGSO卫星非滑动式插值效果

图7 IGSO卫星滑动式中插值效果
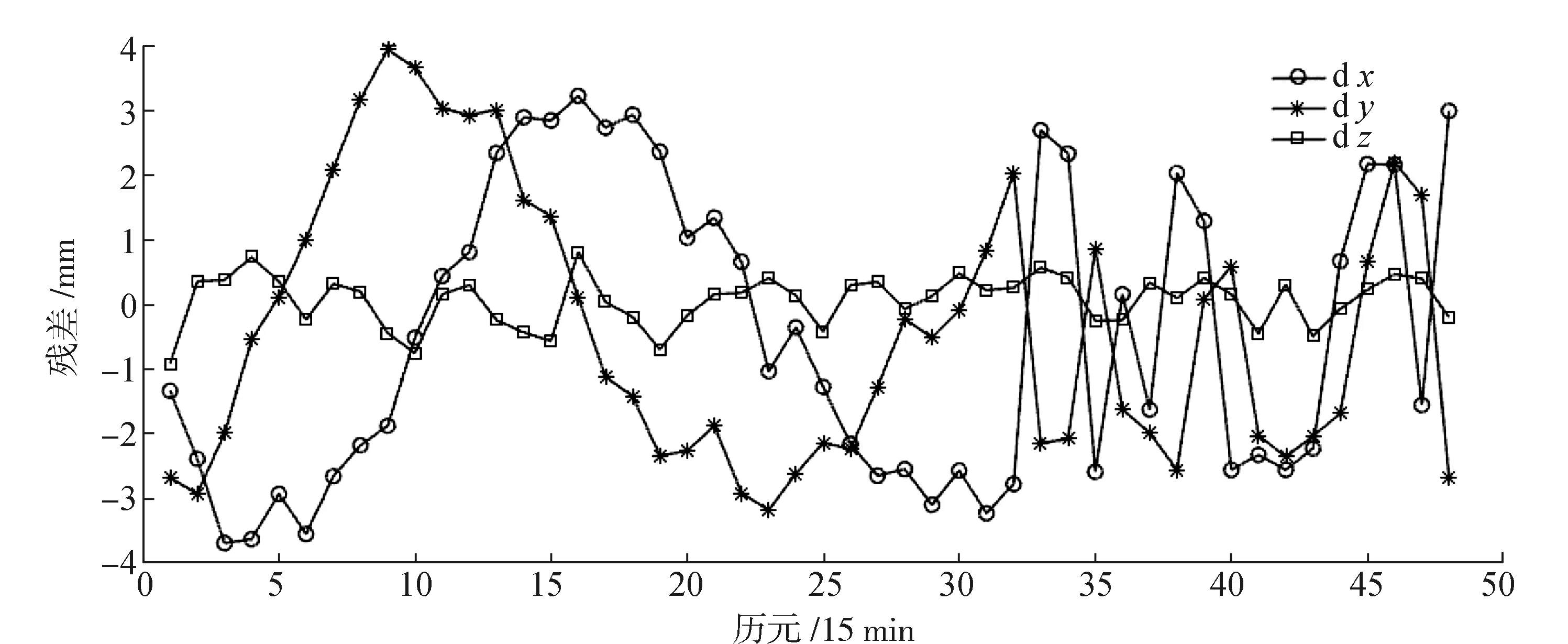
图8 IGSO卫星9阶滑动式插值残差分布图
通过表3数据对比可以看出,非滑动式Lagrange插值方法精度达到最佳时,GEO卫星X,Y,Z坐标分量残差RMS值分别为92.99 mm、79.23 mm、7.40 mm,而滑动式Lagrange插值方法插值精度最佳时GEO卫星X,Y,Z坐标分量残差RMS值分别为0.98 mm、0.69 mm、0.38 mm。从图11可以看出,MEO卫星13阶滑动式Lagrange插值的残差在区间[-10,8]范围内波动,Y坐标分量残差波动相对剧烈些。
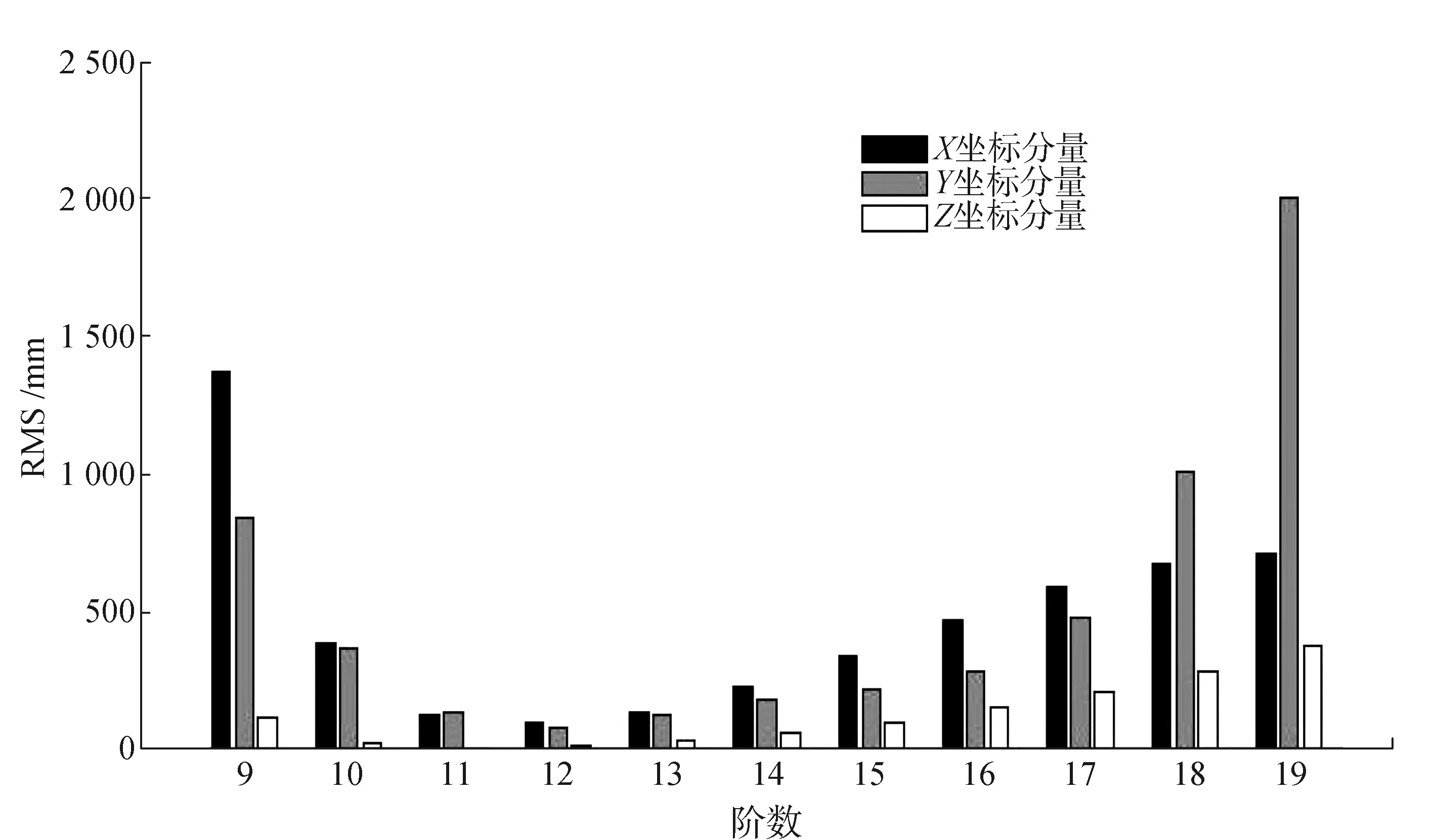
图9 MEO卫星非滑动式插值效果
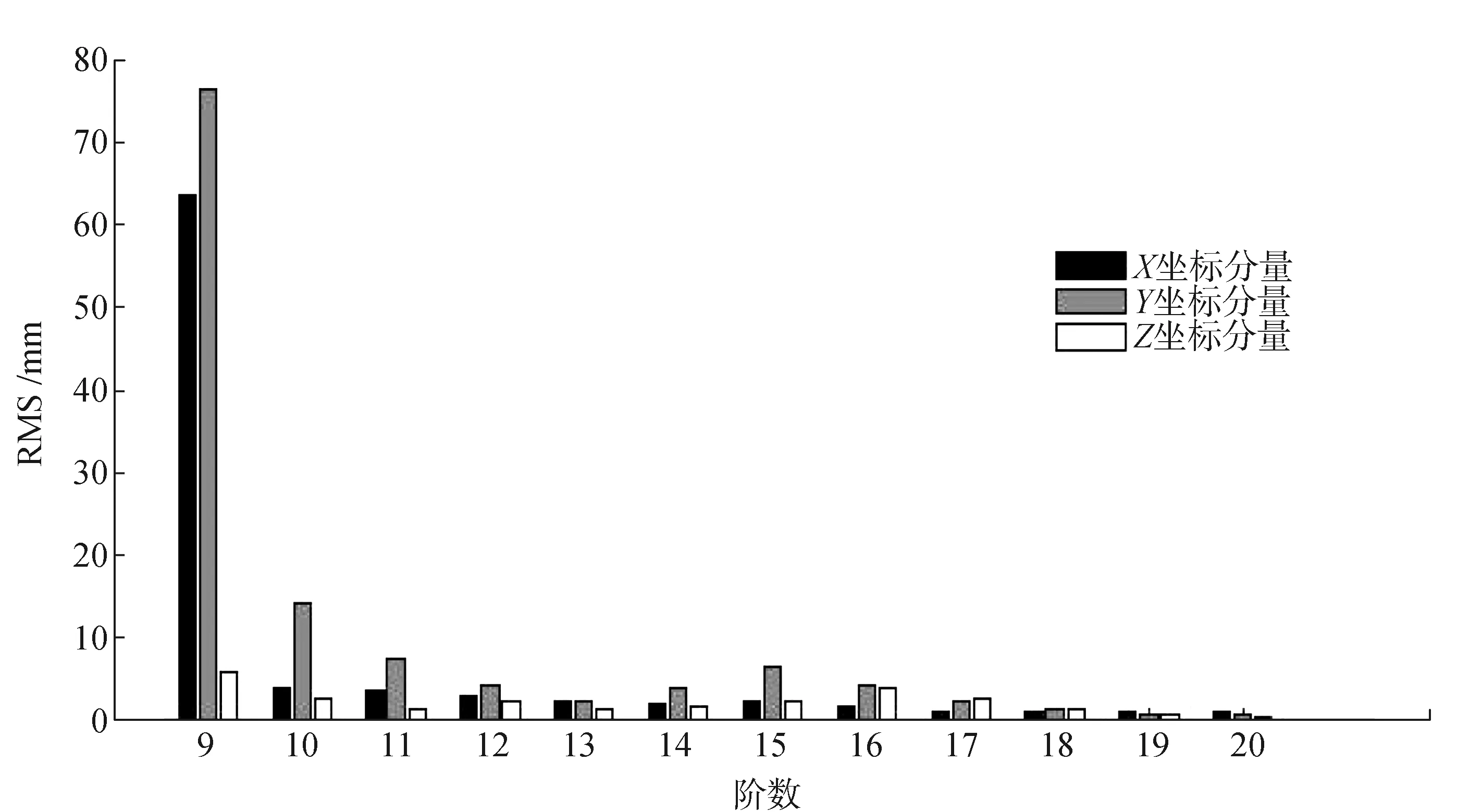
图10 MEO卫星滑动式内插效果
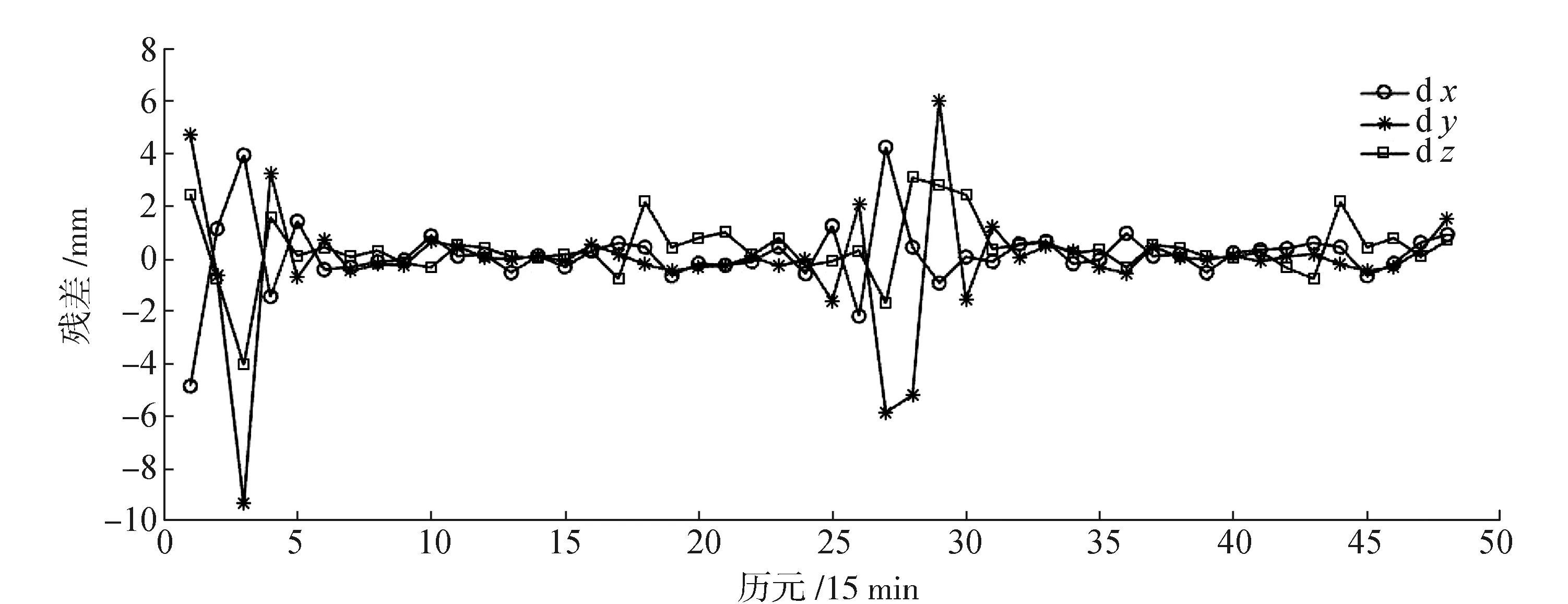
图11 MEO卫星13阶滑动式插值残差分布图
3 结束语
基于非滑动式和滑动式Lagrange插值方法,分别对BDS的GEO、IGSO、MEO 3种不同类型卫星精密星历的三维坐标进行内插,实验结果分析表明:
1)非滑动式Lagrange插值方法内插BDS卫星精密星历时,插值阶数过低或者过高,插值精度效果都较差;滑动式Lagrange插值方法随着插值阶数的提高,插值精度效果逐渐变好,最后趋于稳定。对于不同类型卫星插值精度达到最佳时,插值阶数不相同,同一类型卫星不同的坐标分量插值达到最佳精度时的插值阶数也不相同。
2)非滑动式Lagrange插值方法对GEO卫星在6阶时达到mm级精度,对IGSO在11阶时达到mm级精度,对MEO卫星在12阶时达到cm级精度;滑动式Lagrange插值方法,对GEO卫星在6阶时达到mm级精度,对IGSO卫星在9阶时达到mm级精度,对MEO卫星在11阶达到mm级精度。不同插值方法在同一插值阶数时,滑动式Lagrange插值方法插值精度明显优于非滑动式Lagrange插值方法。

