Structural Finite Element Software Coupling Using Adapter Elements

Andreas H.Schellenberg ,Yuli Huang and Stephen A.Mahin

Abstract: This paper describes a versatile and computationally efficient method for coupling several finite element analysis (FEA) programs together so that the unique modeling and analysis capabilities of each code can be utilized simultaneously to simulate the static or dynamic response of a complete numerical system.An arbitrary number of finite element analysis software packages can be coupled by adding two special types of elements,namely generic and adapter elements,to each of the finite element applications using their programming interface.These elements are inserted at the interfaces between the different sub-domains of the complete system modeled by each finite element analysis software package.Exchange of data between the coupled FEA codes is accomplished in a modular and synchronized manner using OpenFresco (Opensource Framework for Experimental Setup and Control).OpenFresco is an objectoriented,environment independent software framework initially developed for hybrid simulation in which certain aspects of a complete structure are simulated numerically and other aspects are simultaneously tested physically.An important practical advantage of this coupled analysis approach is that all of the connected FEA codes run concurrently and continuously,decreasing analysis time consumption by an order of magnitude or more compared to more traditional approaches that shut down and restart the coupled analysis codes at each integration time step.The implementation and accuracy of this approach to FE software coupling are demonstrated using dynamic analyses of three simple structural models from the field of earthquake engineering.

Keywords: Software coupling,co-simulation,adapter element,OpenFresco.

1 Introduction

Finite element analysis (FEA) software packages are widely available to numerically simulate the static and dynamic response of structural systems.Many of these software packages are highly specialized,and provide excellent modeling and analysis capabilities for particular research or engineering applications.However,available FEA codes may lack specific features needed to model all of the key attributes of a problem of interest.While new models can be added,many users lack the resources to develop,install and verify new elements for an existing FEA code.As a result,there is increasing need to couple specialized software packages together so that the unique modeling and analysis capabilities of each package can be used in the simulation of a particular problem.

A simple example illustrating a case where coupling of FEA codes might be of benefit is shown in Fig.1.The structure consists of a three-story,four-bay welded steel momentresisting frame that is combined with a three-story reinforced concrete shear wall.Software coupling becomes a viable approach,if the analyst does not have access to software that can model both parts of the structure with a comparable degree of refinement,but has two finite element analysis codes,where one has excellent steel frame and panel zone element modeling capabilities and the other has superior reinforced concrete shear wall element modeling capabilities.Even more compelling examples can be imagined where coupling of the most suitable finite element analysis software packages from different disciplines is performed to provide more flexibility and greater fidelity in simulating large engineering systems than may be possible with a single program.In addition,the software coupling provides a framework for structural multiscale analysis,i.e.,coupling analysis of structures at different levels of discretization.Lastly,there is an opportunity for fostering collaboration on large projects where analysts having different expertise focus on different parts or aspects of a structure.These experts may wish to use different software packages due to their familiarity with the FEA codes or the improved modeling capabilities of certain codes compared to others.

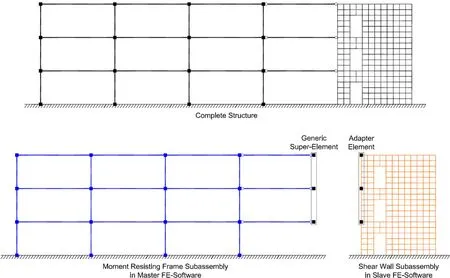
Figure 1:Coupled simulation of three-story example structure

A simulation method that couples two or more displacement-based structural finite element analysis programs together is discussed herein.Often times such a simulation approach where software packages run simultaneously and exchange data at the interfaces of their domains is also referred to as co-simulation (co-operative simulation).

It is important to notice that a coupled simulation that utilizes multiple instances of the same finite element program is simply a special case of the proposed approach.This approach can be used to conduct hybrid or hardware-in-the-loop simulations where various portions of a structure are modeled numerically in different FEA codes and physically in one or more laboratories.Although the theory presented in this paper is specialized for the finite element analysis of structural problems,the same idea is applicable to the finite element analysis of partial differential equations that arise in other environments,such as mechanical,hydraulic,thermal,electrical and chemical systems.

After introducing the basic concept of finite element analysis software coupling,the theory for the proposed adapter element approach is presented.The theory is presented in two parts where a more intuitive approach to the coupling problem is shown first and then a more rigorous approach based on the penalty method is discussed second.By comparing the resulting equations,it can be seen that both approaches lead to the same solution.The use of the Open-source Framework for Experimental Setup and Control (OpenFresco) [Takahashi and Fenves (2006);Schellenberg,Mahin and Fenves (2007);Schellenberg,Mahin and Fenves (2009)] as the middleware connecting the coupled FEA codes is then described,as is the implementation of adapter elements into the Open System for Earthquake Engineering Simulation (OpenSees) [McKenna (1997);Fenves,McKenna,Scott et al.(2007)] as well as the LS-DYNA [LSTC (2007)] and Abaqus [Dassault Systèmes (2012)] commercial finite element software packages.Finally,to demonstrate and verify this approach to coupling finite element codes,three structural examples from the field of earthquake engineering are presented.

2 Finite element software coupling concept

For the co-simulation approach developed herein,multiple finite element software packages are coupled together to seamlessly simulate the response of the combined system.To achieve this,one of the finite element programs is selected as the master and all the other programs act as slaves.The master program is responsible for driving the analysis.Typically,some portions of the structure are directly modeled in the master program,but this is not required for this co-simulation approach to function correctly.The remaining structural subassemblies that are not represented in the master program are implemented and analyzed in one or more slave programs.Each of these slaved subassemblies is acting as a super-element and is connected to the master program via the exchange of a set of response variables at the interface degrees of freedom.During a cosimulation,the master program is responsible for computing response quantities at the interface degrees of freedom and communicating them to all the slave programs.The salve programs are responsible for simultaneously imposing these response quantities on their subassemblies and for returning the corresponding work conjugates.If available it can be advantageous if the slave programs also return the stiffness or flexibility matrix of the super-element.For the structural analysis applications described herein,the response quantities that are to be exchanged at the interface degrees of freedom can be displacements,velocities,accelerations,or tractions or a combination of these variables.For the adapter element theory that is presented in this paper,it was assumed that displacements are sent from the master to the slave programs and forces and stiffness matrices are returned from the slave programs to the master.

The required communication of response quantities from the master to the slave programs is realized by implementing generic super-elements within the master program that represent the slaved subassemblies.In the slave programs it is necessary to implement adapter elements that facilitate imposing the prescribed response quantities at all the interface degrees of freedom.Middleware or coordinator software is then utilized to connect the generic super-elements in the master program with the corresponding adapter elements in the slave programs.Besides the necessary communication methods,the middleware software can also provide supplemental data storage,system control,optimization,and data transformation functionalities.The middleware deployed in this paper is the Open-source Framework for Experimental Setup and Control [Takahashi and Fenves (2006);Schellenberg,Mahin and Fenves (2007);Schellenberg,Mahin and Fenves (2009)].OpenFresco is an object-oriented software framework supporting the development and deployment of the hybrid simulation experimental testing method.The framework,which was originally developed to interface finite element analysis software programs with physical specimens in one or more laboratories,can readily be deployed to provide the required communication between master and slave programs.OpenFresco consists of a number of software objects (i.e.,sites,communication channels,transfer system setups,as well as control and data acquisition interfaces) to provide a modular and structured approach to interfacing finite element software.Hence,the OpenFresco middleware supports hybrid simulations and co-simulations where some parts of the structure are analyzed numerically in one or more computational sites and others are simultaneously tested in one or more experimental sites (i.e.,physical laboratories).

In terms of structural multi-scale analysis,the master program analyzes the complete structure where every member is represented by a single element,while the slave programs analyze individual components that are more vulnerable to structural failure,with multiple elements representing each structural member.This means that the complete structure is analyzed at multiple levels of discretization.The remainder of this paper discusses the coupling of multiple finite-element programs for purely analytical cosimulations without experimental subassemblies in laboratories.For an in-depth discussion of how OpenFresco provides the means to couple analytical and experimental subassemblies to carry out hybrid simulations,the interested reader is referred to Schellenberg et al.[Schellenberg,Mahin and Fenves (2009)].

While the co-simulation method developed in this paper uses super- and adapter-elements to exchange response quantities among the coupled software,several other approaches have been suggested and implemented to facilitate the coupling.Some researchers utilize a file system [Wang,Nakashima and Pan (2006);Kwon,Nakata,Park et al.(2007);Elmekati and Usama (2010);Zhang,Pan,Gu et al.(2014)] in the following manner.To send prescribed response quantities at the interface degrees of freedom from the master to the slave program,the master program writes such trial values to special communication files at every time step.All the slave programs are then started and read relevant information about past and current states from these files and perform one analysis step.Once each slave program completes the analysis of the current step,results are written back to the communication files and program execution is terminated.Finally,the master program reads the information from the communication files and completes its own analysis step.Other software developers have made program-specific modifications to commercial finite element analysis software and multibody dynamics software to provide co-simulation capabilities [MSC Software (2014);Dassault Systèmes (2012);ANSYS (2014)].However,these co-simulation capabilities were made for a limited number of specific software packages and they required the developers to have access to the entire source code of the software packages to add the co-simulation capabilities.Furthermore,these co-simulation schemes typically only provide coupling between two software packages,whereas the proposed method does not have this limitation and can couple any number of software packages.For multiphysics applications several of these specialized co-simulation interfaces use strong coupling approaches where elements are required to carry all degrees of freedom from the different physical fields.A more general meshbased parallel code coupling interface (MpCCI) was developed by Fraunhofer SCAI [Fraunhofer SCAI (2014)].The co-simulation interface is available for many software packages and uses network socket connections to exchange data through a central coupling server that coordinates the control flow.Adapter Application Programming Interfaces (APIs) then provide the connections to the different software packages through their standard code APIs.In contrast,in the approach proposed herein,generic super- and adapter-elements accomplish the data exchange directly,without using any central coupling server.Using standard programming interfaces (e.g.,user-defined elements) that are provided with many commercial finite element analysis programs,generic super- and adapter-elements need to be implemented just once far a given finite element software.OpenFresco,the open-source middleware,is then deployed to manage communications.This approach provides the advantage that all of the connected codes run continuously and concurrently,without the need to terminate and restart processes,ultimately increasing computational efficiency significantly.In addition,it makes it possible for users to customize the coupling based on their needs.Generic super- and adapterelements are currently available through the OpenFresco software framework for OpenSees,LS-DYNA,Abaqus,ANSYS,MATLAB and Simulink.

3 Theory of adapter elements

3.1 Intuitive approach

As discussed in Section 2,each slaved subassembly is discretized in space and analyzed in a slave program.For each individual subassembly the governing semi-discrete equations of motion in matrix form are given by Eq.(1).

where M is the global mass matrix,Pris the global resisting force vector,and P is the global load vector.They are respectively given by

In Eq.(2),Mlumpedrepresents the lumped nodal masses,Plumpedare the lumped nodal loads,refers to the finite element assembly process of the elemental contributions of the mass mel,the element resisting forces due to internal stresses pr,el,and the element loads p0,eldue to body forces b,boundary tractions t,non-mechanical strains ε0and initial stresses σ0,which are evaluated following Eq.(3).

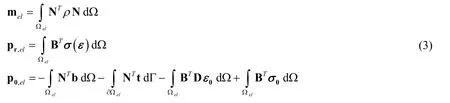
In the above equations,the matrix N represents the shape functions,the matrix B the strain-displacement transforms,the matrix D the constitutive relations,andΩelis the elemental domain.The way the master program drives the slaved subassemblies is to prescribe the displacements at the interface degrees of freedom followed by the measurement of the corresponding resisting forces.To this end,a linear-elastic adapter element is appended to the subassembly modeled in the slave program.The adapter element connects to,drives,and obtains reactions from all the nodal interface degrees of freedom.The effective stiffness of the adapter element,measured as the resisting force divided by the error of displacement prescription,should be two to three orders of magnitude larger than the stiffness of the subassembly,such that the interface degrees of freedom movement can be precisely driven.This concept is analogous to a transfer system that is typically employed in an experimental laboratory test:the boundary conditions on an experimental subassembly are imposed by actuators with high oilcolumn stiffnesses combined with nearly rigid loading frames.The element load vector due to imposed displacements can be evaluated according to Eq.(4).

whereκis the stiffness matrix of the adapter element.Comparing Eq.(3c) with Eq.(4),similarity can be observed between the imposed displacement and the non-mechanical strains,the difference being that the former is time-varying and the latter is a constant initial condition.It is also implied in Eq.(4) that there are no body forces,boundary tractions,initial strains and initial stresses acting on the adapter element.Finally,the elemental force vector,which provides input to the slave program for assembly of the unbalanced forces,is the combination of the forces due to the adapter element deformations and the imposed displacements.

The resisting force vector corresponding to the prescribed displacement vector,,and to be returned to the master program once the equilibrium is established in the slave program,is the negative of the above equation -padpt.The displacements imposed on the subassembly are equal to the adapter element nodal displacements,uadpt,and are generally not identical to the prescribed displacement targets received from the master program.The stiffer the adapter element is relative to the subassembly,the smaller the discrepancy that is being observed between prescribed target values and actual imposed values.This concludes the intuitive theory of the adapter elements.A more rigorous derivation of the theory that is based on the penalty method and leads to the same results is discussed in the next section.

3.2 Penalty-based approach

The theory of adapter elements can also be derived based on the penalty method.For the sake of clarity,the derivation for a linear system undergoing a static analysis is presented first.The governing equations in matrix form are given in Eq.(6) for a linear structure consisting ofndfree degrees of freedom.

where displacement vector u ∈Rnd,load vector P ∈Rndand stiffness matrix K ∈Rnd×nd.For the finite element approximation

where matrices D and B are associated to the strain-displacement transforms and constitutive relations,and Ωelis the elemental domain Eel.

With a positive definite assumption for the stiffness matrix K,the stated problem in Eq.(6) can be rewritten in variational form,i.e.,the solution of the displacement vector u can be obtained as the stationary point of the following potential

In the coupled simulation,the master program drives the slaved subassemblies by prescribing the displacements at the interface degrees of freedom.This is achieved by imposing an additional constraint to the system:for degrees of freedom i,ui=,∀i∈Nadpt,where Nadptis the set of degrees of freedom and its size isnadpt.This constraint is formulated as

Next,the constrained system is solved by the penalty method,i.e.,defining the penalized potential as

where the penalty matrixκis positive definite.The physical meaning of the penalty may be interpreted as a very stiff spring that correlates to the high actuator stiffnesses described in the previous section.The penalty matrix is defined as

whereki＞ 0 is the penalty stiffness at thei-th degree of freedom of the adapter element.The solution to the constrained problem can be found as the stationary point of the penalized potential Πκthat is still quadratic in u.The stationary point uκcorresponds to a minimum of the potential,meaning that the first variation vanishes

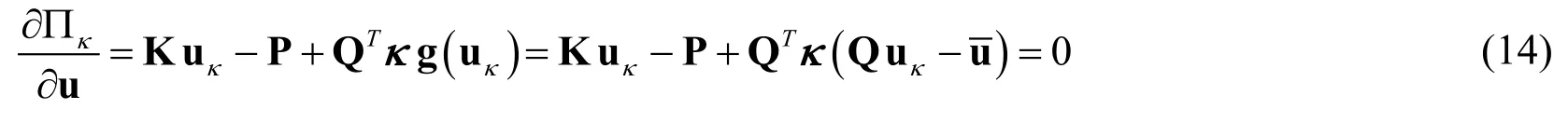
or,equivalently,

Denoting the errors in the approximate solution as eu= uκ-u and the smallest eigenvalue of the penalty matrix asκmin,a rigorous analysis can prove the convergence of the penalty method,i.e.,→0 asκmin→∞,with linear convergence in 1κmin.

Next,the equivalence between the adapter element and the penalty approaches is illustrated.Starting from Eq.(6),the constraint formulated in Eq.(10) is incorporated using anadditionaladapter element Eadpt.The adapter element connects the degrees of freedom in the set Nadpt,with stiffness matrix defined as kadpt=κ,and element load

vector defined as p0,adpt=-κ(see Eq.(4)).A new system with the adapter element has the global stiffness matrix and force vector assembled as

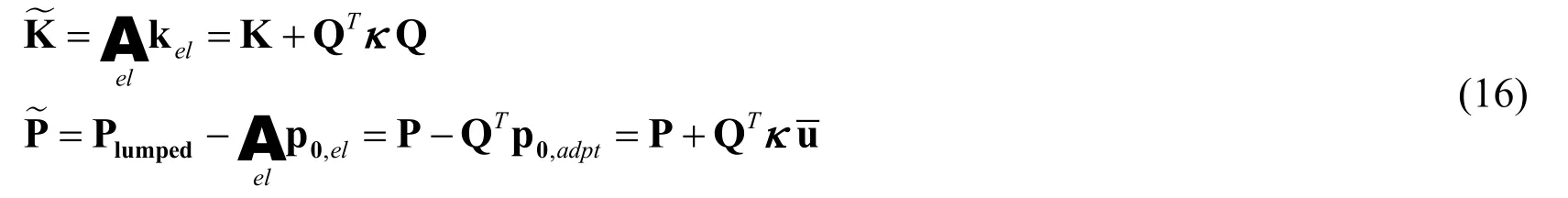
It is worth noting that QTκQ resulted from the assembly operation on the adapter elemental stiffness matrix,and that QTp0,adptresulted from the assembly operation on the adapter elemental load.Finally,Eq.(15) can be rewritten astherefore uκis the exact solution for the new system.This proves that the adapter element method is equivalent to the penalty method.

It can also be shown that the convergence of the penalty method,and hence the adapter element method,is also guaranteed for structures that exhibit nonlinearity and/or inertial effects.For example,for nonlinear static problems,the equilibrium equations are rewritten in the residual form.

where relis the elemental residual force vector,

Let the residual force vector of the adapter element be defined as

where uκ,adptis the displacement vector of the adapter element.Because no other elemental loads are applied to the adapter element in a coupled simulation by design,zero global residual in Eq.(17) implies

Further transformation of Eq.(21) provides the calculation of the overall resisting force from all the regular elements:

Eq.(22) suggests that the resisting force of the slaved subassembly consisting of the regular elements can be extracted as the negative of the adapter elemental force (Eq.(20)).To summarize,the adapter element method serves two closely related purposes:prescribing nodal displacements and obtaining nodal resisting forces of the slave subassembly.Because the equilibrium equations (Eq.(1)) of the subassembly were written in their most general form,including external loads as well as inertia and energy dissipation effects,it is very important that the employed time-integration schemes in the master and slave programs are compatible with each other.This is necessary so that time in the master and slave programs advance in the same format.Explicit or Operator-Splitting methods,which only require one data exchange per integration time step,or the specialized constant number of iteration hybrid simulation integrators,which require a fixed number of data exchanges per time step [Schellenberg (2009)],should be used for the dynamic analysis in the master program.For the dynamic analysis in the slave programs any transient integration method can be used,provided the time step sizes are compatible with the master integration method.On the other hand,if the behavior of the subassembly in the slave program is time independent (no inertia and energy dissipation effects) a static integrator should be employed in the slave program and any integration method can be utilized for the static or dynamic analysis in the master program.

4 Implementation of coupled simulation through adapter elements

Next,the operations of the different modules of a coupled simulation and the interactions among them are discussed in terms of a three-story example structure.As shown in Fig.1,the structure consists of a three-story,four-bay steel moment resisting frame that is combined with a three-story concrete shear wall.

This structure is an ideal candidate to be analyzed by two finite element analysis codes,where one of them has excellent frame element modeling capabilities and the other one has superior shell element modeling capabilities.The steel moment resisting frame subassembly is analyzed in the master FE-software and the concrete shear wall subassembly is analyzed in the slave FE-software.Because the moment resisting frame is connected to the shear wall through three interface nodes,a generic 3-node super-element is added to the master program.Hence,this element represents the wall in the master model.As shown in Fig.1,the 3-node adapter element connects to the interface nodes of the shear wall subassembly in the slave program and is responsible for imposing trial displacements on such subassembly.The few beam-column elements that are utilized to model the moment frame in the master program versus the many shell elements that are utilized to model the shear wall in the slave program,demonstrate a multiscale analysis with two levels of discretization.

The sequence of operations and the data exchange necessary to achieve the coupling between the master and slave FE-software is shown in Fig.2.Starting on the side of the master program,the super-element receives a vector of global trial displacements usuper=uelfor all its degrees of freedom form the master integration method.It then sends these displacements using a TCP/IP or UDP socket to the OpenFresco simulation application server.The experimental site and setup modules are responsible for storing and transforming the response quantities if necessary.However,for the example structure presented here,no transformations of the trial displacements and the resisting forces are required,meaning that the NoTransformation experimental setup is utilized.The trial displacements are next passed to the SimFEAdapter experimental control object that provides the connection to the adapter element utilizing a TCP/IP or UDP socket.The adapter element then combines the received displacementswith its own element displacements uadpt=uelfrom the subassembly.Subsequently,the element force vector pel=padptof the adapter element is updated using Eq.(5) and returned to the subassembly.Once the equilibrium solution process of the slave program has converged,the negative of the element force vector -padptis returned to the SimFEAdapter experimental control object across the TCP/IP or UDP socket.The experimental site and setup modules are again responsible for storing and transforming the response quantities.The simulation application server then returns the force vector through the TCP/IP or UDP socket to the super-element in the master program.Finally,the super-element saves them as element forces pel=psuperand returns them to the master integration method,which is then capable to determine the new trial displacements and proceed to the next time step.It is important to notice that both the super-element in the master subassembly and the adapter element in the slave subassembly can be implemented as user-defined elements into each finite element program using their standard published programming interfaces.

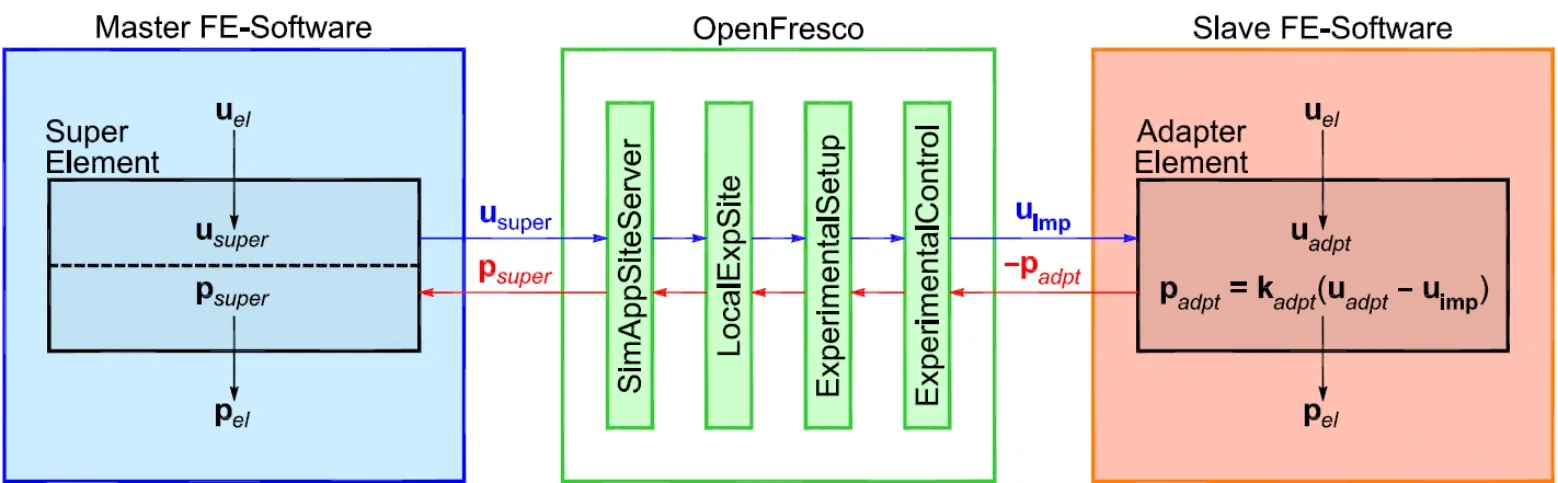
Figure 2:Sequence of operations and data exchange

5 Example applications

5.1 Coupled simulation of a cantilever column

This and the following two sections demonstrate how adapter elements can be used in coupled simulations and assess the accuracy of such approach.In this section,a fixedbase steel column with a lumped mass at its tip was comparatively analyzed employing a monolithic versus the coupled approach (see Fig.3).The total height of the column is 2,000 mm.The column cross-section is a square steel tube with an outer depth of 350 mm and a wall thickness of 12 mm.The bi-linear steel material has a Young’s modulus of 205 GPa,a yield stress of 235 MPa and a hardening ratio of 1.0E-4.The lumped mass at the tip of the column is 101,937 kg,which corresponds to a gravity load of 1,000 kN.No damping was assigned to the structure.This structure is compatible with that in Tada et al.[Tada and Pan (2007)].

The structure was discretized into two frame elements A and B.As shown in Fig.3,the upper beam-column B is 1,300 mm high,and the lower beam-column A is 700 mm tall.The force-based “ForceBeamColumn” Element formulation in OpenSees was used for both frame elements,even though the upper beam-column B was supposed to remain elastic.Geometric nonlinearity was considered using the large-displacement “Corotational Transformation” in OpenSees.Two quasi-static pushover analyses were conducted.The top displacement of the column was imposed at a constant speed of 0.1 mm/sec,and the target displacement was 100 mm at 1,000 seconds.The time step size for both analyses was 1 second,so the total number of time steps was 1,000.

In the monolithic analysis,the complete model was analyzed in a single instance of OpenSees and the implicit Newmark method was utilized to integrate the equations of motion.In the coupled analysis,the lower beam-column A was analyzed in one OpenSees instance,and connected to the master structure via an adapter element in terms of two translational and one rotational degrees of freedom.The master structure,consisting of the upper beam-column B and a generic super-element A’,representing the lower beam-column A,was analyzed in a second instance of OpenSees.

Figure 3:Structural model for cantilever column

For the coupled analysis theAlphaOSintegration method was adopted to solve the equations of motion.In contrast to an explicit integration method theAlphaOSmethod requires a stiffness matrix for the generic super-element in the master program.Similar to hybrid simulation approaches,the initial instead of the tangent stiffness of the generic super-element can be employed [Schellenberg,Mahin and Fenves (2009)] and such stiffness matrix can be determined before conducting a coupled simulation.The initial stiffness matrix for the three interface degrees of freedom can be computed from the following equation.

Alternatively,the tangent stiffness matrix of the generic super-element can be estimated based on the incremental displacements and forces from the slave program using quasi-Newton methods.This approach,which has been employed in hybrid simulations,is described in detail by Kim [Kim (2011)].Because displacement and force measurements from the slave program do not have to deal with noise from instruments (like in hybrid simulations),these quasi-Newton methods provide more accurate estimates of the tangent stiffness matrix.Several of these approaches for estimating tangent stiffness matrices are available in OpenFresco.However,for the example presented here,the initial stiffness matrix was utilized and it was computed based on Eq.(23).

The base shear versus horizontal displacement at the top end of element A (which is the first interface degree of freedom) is compared in Fig.4.Excellent agreement between the two types of analyses was observed.

Figure 4:Comparison of load-displacement curve

5.2 Coupled simulation of a structural subassembly

The purpose of the second example is to demonstrate that the proposed co-simulation approach not only applies to open-source finite element software but also works well with commercial finite element software as long as such software provides a standard programming interface (e.g.,user-defined elements).To this end,the following four cosimulations were performed using LS-DYNA v971 [LSTC (2007)] and Abaqus v6.12 [Dassault Systèmes (2012)].

Table 1:Co-simulations using commercial FE software

LS-DYNA’s and Abaqus’s user-defined element interfaces were employed to implement the super elements for the master programs and the adapter elements for the slave programs.Both of these commercial FE software packages use the FORTRAN programming language to provide the user-defined element interface.In addition to the OpenSees,LS-DYNA,and Abaqus software packages,super and adapter elements have also been implemented in ANSYS,MATLAB,and Simulink.The source code for all of these super and adapter element implementations is freely available through the OpenFresco software distribution.

As shown in Fig.5,the model that was used for the four coupled simulations consists of two columns,Element 1 and 3,connected by a spring,Element 2.Lumped masses are placed at the top of each column,where the mass at node 3 is 0.04 kip-sec/in.and the mass at node 4 is 0.02 kip-sec/in.In addition 5% mass-proportional damping was assigned at these two nodes.The nonlinear column on the left was modeled in the slave program and the linear spring and the linear column on the right as well as the two masses were modeled in the master program.The nonlinear column in the slave program was modeled with a bi-linear hysteretic behavior with an initial stiffness of 2.8 kip/in.,a yield strength of 0.95 kip,and a post-yield stiffness ratio of 0.105.The linear spring in the master program was assigned a stiffness of 2.0 kip/in.and the linear column on the right had a stiffness of 5.6 kip/in.For the adapter element in the slave program a penalty stiffness of 1.0E12 kip/in.was used.The structure was subjected horizontally to the north-south component of the ground motion recorded at a site in El Centro,California during the Imperial Valley earthquake of May 18,1940.The ground acceleration history had a time interval of 0.02 seconds and a peak ground acceleration of 0.32 g.For the dynamic analysis in the master program theExplicit Newmarkmethod was adopted to solve the equations of motion.Because theExplicit Newmarkmethod does not require a Jacobian,it was not necessary to determine the stiffness matrix of the generic superelement.

From the four simulations,the displacement histories in the horizontal direction at Node 3 and the hysteresis loops of the left column analyzed in the slave program are shown and compared in Fig.6.As can be seen,the four displacement histories and hysteresis loops are essentially identical.

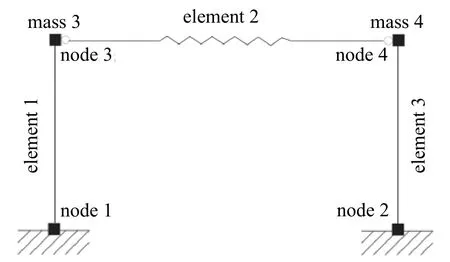
Figure 5:One-bay frame example structure

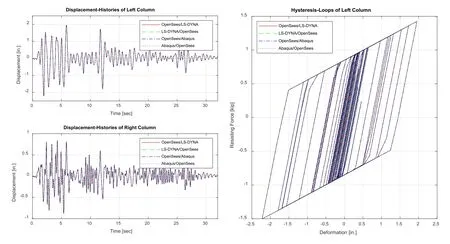
Figure 6:Comparison of displacement histories

5.3 Coupled simulation of a dual-system structure

In this section,the coupled simulation of a dual-system structure,as well as the concept of structural multiscale analysis,is illustrated.Two instances of the software framework Open System for Earthquake Engineering Simulation (OpenSees) were employed.The first instance acted as the master program and the second one as the slave program.As shown in Fig.7,the complete structural model consisted of a three-story,four-bay steel moment resisting frame and a three-story concrete shear wall.The bay widths and story heights of the structure are 30 ft.and 13.5 ft.,respectively.All the columns of the moment resisting frame are fixed at the base.Both beams and columns were modeled by nonlinear force-based beam-column elements with fiber cross-sections and five integration points were used along the length of the elements.The steel fibers had a yield strength of 50 ksi and theSteel02(Giuffré-Menegotto-Pinto) uniaxial material in OpenSees was used to model the hysteretic behavior.The beams in the bay adjacent to the shear walls are not moment-connected and were therefore modeled as linear-elastic truss elements.The concrete shear wall has a thickness of t=24 in.and was modeled by nonlinear layered shell elements.ThePlaneStressUserMaterialin OpenSees was used to model the concrete with a compressive strength of 4 ksi and the Steel02 uniaxial material was used to model the vertical and horizontal steel reinforcement with a yield strength of 60 ksi.For each story of the wall 12×6 such elements were utilized and the three door openings are 5×9 ft.in size.The total weights of the first,second and third floors are 3,950 kip,3,950 kip and 3,250 kip,respectively.Lumped masses were assigned to all the nodes according to those floor weights.Since it was assumed that the floor diaphragms are rigid in plane,equal degree of freedom multipoint constraints were utilized among the nodes of each floor to constrain horizontal translations together.

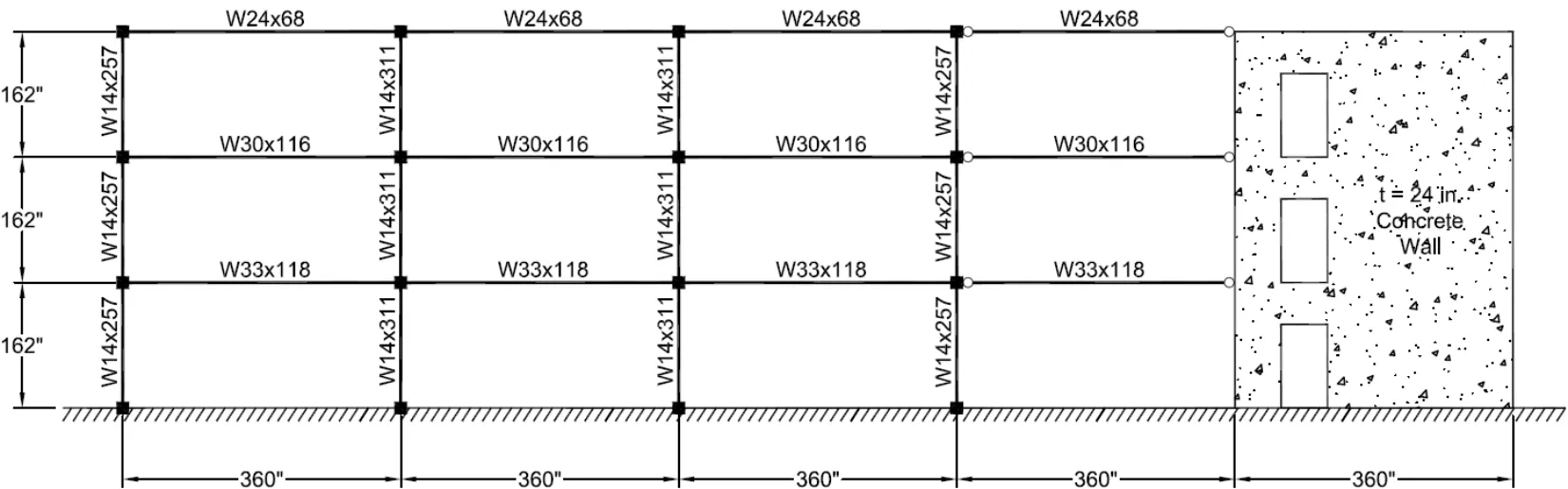
Figure 7:Three-story five-bay frame example structure

As shown in Fig.1,the four bays of the steel moment resisting frame were analyzed in the master program and the three-story concrete shear wall was analyzed in the slave program.The generic super-element,which represented the shear wall in the master FEA software,connected the three interface nodes at the ends of the truss elements.For simplicity only the horizontal degrees of freedom at such nodes were utilized,meaning that the vertical and rotational degrees of freedom were restrained.The 3×3 initial stiffness matrix of the generic super-element needs to be specified by the user.Such matrix can be determined from the shear wall subassembly by imposing unit displacements at one interface degree of freedom at a time,while restraining the remaining interface degrees of freedom.Applying this procedure the following generic super-element stiffness matrix was determined.

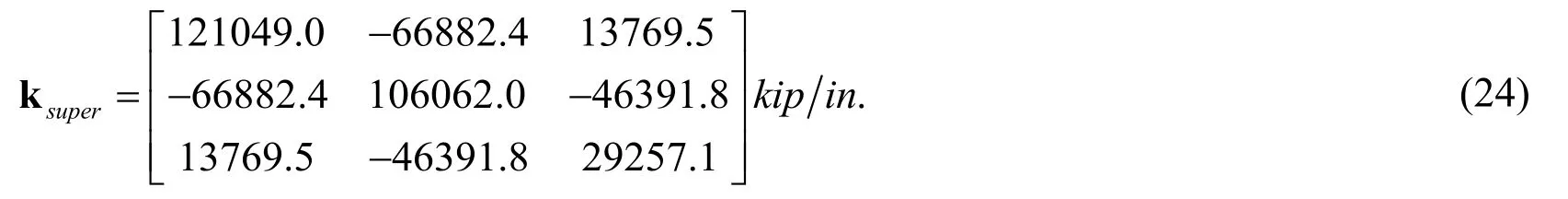
On the other hand,the stiffness matrix of the adapter element in the slave finite element software is not determined from the physical properties of the master subassembly.Instead,high penalty stiffness values for the diagonal elements of the matrix are assigned arbitrarily,while keeping in mind that very large stiffness values could cause numerical problems and smaller stiffness values will reduce the accuracy of the imposed displacements.For the example presented here,1.0E12 kip/in.stiffness values were assigned to the three diagonal entries of the adapter element stiffness matrix.These were found to produce good accuracies without causing any numerical problems during the analysis.

With the stiffness matrix of the generic super-element available,it was possible to perform an eigenvalue analysis to determine the periods and mode shapes of the entire structure.The periods of the three horizontal mode shapes turned out to be T1=0.2842 seconds,T2=0.0791 seconds and T3=0.0452 seconds.The mode shapes are shown in Fig.8.For the dynamic analysis the viscous energy dissipation was modeled considering 5% mass proportional damping.The structure was subjected horizontally to the SACNF01 near-fault ground motion of the SAC steel project,which corresponds to the 1978 Tabas earthquake scaled to a peak ground acceleration of 0.63 g.For the dynamic analysis in the master program the Newmark method was employed to solve the equations of motion and for the static analysis in the slave program the Load Control integration method was adopted.The integration time step size in the master program was chosen to be Δt=0.01 seconds.

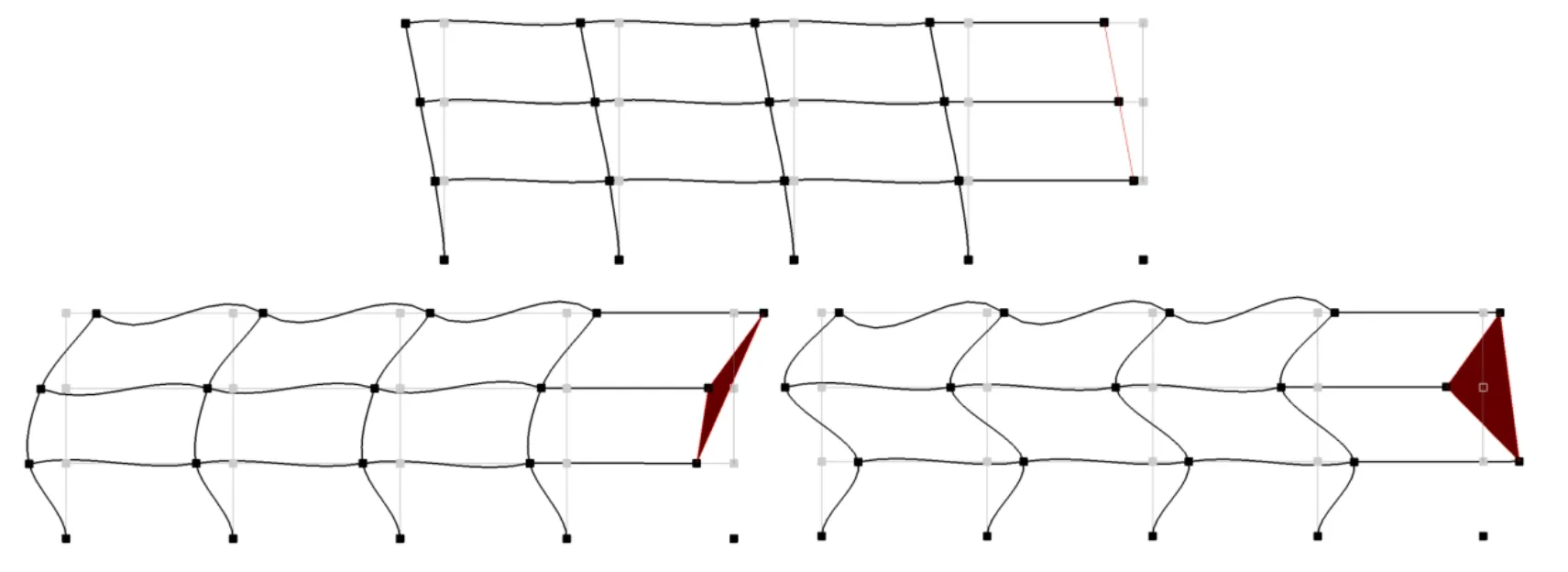
Figure 8:1st,2nd,and 3rd horizontal mode shapes determined from coupled analysis

To validate the coupled dynamic analysis results and assess their accuracies,the complete structure was also analyzed in OpenSees.The horizontal displacement,velocity and acceleration time histories of the third floor diaphragm are shown in Fig.9.As can be seen,the displacement,velocity and acceleration histories of the coupled simulation and the complete simulation are nearly identical,which illustrates the feasibility and accuracy of the adapter element approach for performing coupled simulations of nonlinear systems under dynamic loading conditions.Also,the wall deformations at the maximum horizontal roof displacement of dr,max=3.73 in.at time t=6.63 seconds,are nearly identical.

Figure 9:Comparison of third floor response histories and wall deformations at t=6.63 s

Finally the analysis time consumptions are compared between the complete simulation in OpenSees and the coupled simulation using two instances of OpenSees.In both cases elapsed times were measured for the 2500-step-long transient analyses.For the coupled analysis this corresponded to a total of 27,976 network transactions across the TCP/IP connection between the two programs.As can be seen from Tab.2,the coupled simulation is only about two times slower than the simulation of the complete structure.

Table 2:Comparison of analysis time consumptions

6 Conclusion

The adapter element approach,combined with the OpenFresco middleware,provide a useful and effective set of modules for coupling structural analysis software.The adapter elements developed herein,illustrate a novel application of user-defined elements,offering an effective technique for users to couple different finite element analysis software packages together.Coupling is important in the simulation of large structural systems that require the unique modeling capabilities of different analysis programs.Three examples of increasing complexity demonstrated the implementation and accuracy of the adapter element concept for static pushover analyses as well as nonlinear dynamic analyses.The approach avoids the need to repetitively shutdown/restart programs and read/write data files,thereby substantially reducing the time needed for coupled simulations compared to many current approaches used for coupling software.

Acknowledgement:Funding for this work was provided in part by the National Science Foundation through a subaward from the NEES Consortium,Inc.under Cooperative Agreement CMS0402490.The authors appreciate the assistance of Dr.Frank McKenna of the University of California,Berkeley,Dr.John Hallquist of Livermore Software Technology Corporation,and Prof.Yoshikazu Takahashi of Kyoto University.The findings and conclusions are those of the authors alone,and may not reflect those of the sponsors.