The Behavior of Rectangular and Circular Reinforced Concrete Columns Under Biaxial Multiple Excitation

Mohammad Reza Salami ,Ebrahim Afsar Dizaj and Mohammad Mehdi Kashani

Abstract: The aim of this study is to investigate the dynamic performance of rectangular and circular reinforced concrete (RC) columns considering biaxial multiple excitations.For this purpose,an advanced nonlinear finite element model which can simulate various features of cyclic degradation in material and structural components is used.The implemented nonlinear fiber beam-column model accounts for inelastic buckling and low-cycle fatigue degradation of longitudinal reinforcement and can simulate multiple failure modes of RC columns under dynamic loading.Hypothetical rectangular and circular columns are used to investigate the failure modes of RC columns.A detailed ground motion selection is implemented to generate real mainshock and aftershocks.It was found that multiple excitations due to aftershock has the potential of increasing the damage of the RC columns and longitudinal reinforcements are significantly affected low-cycle fatigue.Also,it was found that rectangular column is more sensitive to accumulative damage due to cyclic fatigue.This study increases the accuracy of structural analysis of RC columns and consequently improves understanding the failure modes of RC columns with different cross-sectional shapes.

Keywords: RC column,biaxial loading,multiple excitations,low-cycle fatigue.

1 Introduction

Catastrophic earthquakes in the past triggered a series of researches and investigations on the performance and safety of RC structures.It was found that columns are the key elements of RC structures.Several experimental and numerical analyses were conducted to understand the damage mechanism of RC columns.However,most of these studies used uniaxial loading.According to Rodrigues et al.[Rodrigues,Arêde,Varum et al.(2013)],the number of experimental tests reported on rectangular RC columns is 397 and 67 for uniaxial and biaxial loading,respectively.This statistical information (although it is collected up to 2013),proves that most of the present-day knowledge of inelastic behavior of RC columns are based on uniaxial loading.As a consequence,threedimensional effects have been mostly ignored in seismic design and analysis of RC buildings.However,it is well-known that the direction of an earthquake is random,and the response of a structure under multi-directional loading is complicated.Therefore,understanding the performance of RC structures under multi-directional excitation is important.The current research on seismic behavior of RC column under biaxial loading is mainly experimental works [Oliva and Clough (1987);Zeris and Mahin (1992);Qiu,Li,Pan et al.(2002);Li,Mander,and Dhakal (2008);Khaled,Massicotte and Tremblay (2011);Lu,Li,Wang et al.(2012);Rodrigues,Arêde,Varum et al.(2013);Germano,Tiberti and Plizzari (2015);Nojavan,Schultz,Haselton et al.(2015);Shirmohammadi and Esmaeily (2015);Jung,Wilcoski and Andrawes (2018)].These experimental studies have shown that the loading paths have a significant influence on seismic behavior of RC columns.Also,it can be concluded that the bearing capacity and stiffness degradation of RC columns are worse than those of RC column under uniaxial loading [Lu,Li,Wang et al.(2012)].In particular,Rodrigues et al.[Rodrigues,Arêde,Varum et al.(2013)] conducted an experimental study and observed the damage of 24 RC columns under uniaxial and biaxial loading.They found that for columns under biaxial loading,damage occurs at lower drift demands in comparison with the corresponding in uniaxial demand and the reduction can be up to 50-75%.

In addition to the bidirectional characteristics of ground motion,multiple events are also another fact which has received extra attention recently.The main event with the highest magnitude is known as the mainshock and the following ground motions in a time window are known as aftershocks.The accumulation of damage and degradation in the structure due to the mainshock and the following aftershocks potentially endanger the safety of residents.The potential of having additional damage due to mainshock-aftershocks (MSAS) have been investigated for RC structures [Faisal,Majid and Hatzigeorgiou (2013);Di Sarno (2013);Ebrahimian,Jalayer Asprone et al.(2014);Goda and Tesfamariam (2015);Abdelnaby and Elnashai (2015);Raghunandan,Liel and Luco (2015);Jeon,DesRoches,Lowes et al.(2015);Salami,Kashani and Goda (2019)].These studies confirmed that there is a lack of conservatism in the safety of conventionally designed structures subjected to multiple earthquakes and more research is warranted in this field.

In the study conducted by salami et al.[Salami,Kashani and Goda (2019)],on the seismic performance of low rise RC buildings under multiple excitations,it was found that aftershocks have a potential to increase the damage of RC columns due to low-cycle fatigue and it is more severe for long duration ground motion caused by subduction earthquakes.Moreover,in an experimental/analytical study conducted by Hachem et al.[Hachem,Mahin and Moehle (2003)] on the seismic performance of RC columns subjected to ground motions they found that columns with short periods might be susceptible to low-cycle fatigue failure.Results indicate that peak response under bidirectional excitation was similar to that predicted unidirectionally,but that increased demands might occur in the short period range,including increased residual displacements.This paper investigates the seismic behavior of rectangular and circular RC columns under biaxial multiple excitations using incremental dynamic analysis (IDA) [Vamvatsikos and Cornell (2002)].Two RC column with rectangular and circular crosssection have been selected with the same stiffness and dynamic behavior.This paper employs an advanced structural modeling technique,which can simulate various features of cyclic degradation in material and structural components using nonlinear fiber beamcolumn elements.The model accounts for inelastic buckling and low-cycle fatigue degradation of longitudinal reinforcement and can simulate multiple failure modes of reinforced concrete structures under dynamic loading.A comprehensive detail of the model is available at Kashani et al.[Kashani,Salami,Goda et al.(2017);Dizaj,Madandoust and Kashani (2018);Salami,Kasani and Goda (2019)].In addition to the advanced structural modeling,a comprehensive ground motion selection accounting for shallow crustal is implemented,as the hypothetical column is assumed to be located in Los Angeles,US.In this paper,conditional mean spectrum (CMS) [Baker (2011)] is used for an accurate ground motion selection.Real as-recorded mainshock-aftershock are used in this study to investigate the impact of multiple excitations.The following section is devoted to a description of the RC column model.The MSAS ground motion selection is explained subsequently and followed by results and discussion at the end of this paper.

2 Reinforced concrete model

In this study,a circular RC column and a rectangular RC column are considered to investigate the impact of biaxial multiple excitations on the nonlinear dynamic response of RC columns.To this end,details of circular RC column is considered to be quite the same to the column 415 from Lehman et al.[Lehman,Moehle,Mahin et al.(2004)].The axial load ratio and consequently the mass of the rectangular column was assigned equally to the circular column.The dimensions of the rectangular column were selected such that it has the same un-cracked fundamental period and lateral stiffness as the circular column accordingly.The details of hypothetical RC columns are tabulated in Tab.1 and shown in Figs.1(a) and 1(b).

Using the OpenSees finite element package [McKenna (2011)],the advanced finite element modeling technique proposed in Kashani et al.[Kashani,Lowes,Crewe et al.(2016)] is employed here to simulate the nonlinear structural behavior of the considered RC columns.In this method,the column is modeled using two elements with a total length of the first element equal to 6Leffwhere Leffis the buckling length.The calculation of Leffis based on the method suggested by Dhakal et al.[Dhakal and Maekawa (2002)].They proposed an iterative procedure,in which the tie stiffness and required stiffness to prevent buckling of longitudinal reinforcement are compared to find the buckling mode and buckling length accordingly.After finding the buckling length of the longitudinal reinforcements,a forced-based element with three integration points and a second element with five integration points are used to model the RC column which can simulate the inelastic rebar buckling.The numbers of fibers and the section discretization method are based on the recommendations provided by Berry and Eberhard [Berry and Eberhard] (2006).For more information regarding the methodology,formulation,calibration and validation of the model please refer to Kashani et al.[Kashani,Salami,Goda et al.(2017);Salami,Kashani and Goda (2019)].Validated against experimental results,this computational modeling technique is capable to account for cyclic degradation of reinforcing bars due to inelastic buckling and low-cycle fatigue failure.To simulate the nonlinear behavior of reinforcing steel,the phenomenological buckling model proposed in Kashani et al.[Kashani,Lowes,Crewe et al.(2015)] is used.

In Fig.1(c),the implemented buckling model is compared with the uniaxial material Steel02 available in OpenSees library.The stress-strain behavior of unconfined concrete cover and confined concrete core in the circular column are simulated using uniaxial material Concrete02 available in OpenSees.In Fig.1(d) the schematic view of constitutive concrete material model is presented.Fig.2 presents the cyclic response of the material models for steel (Hysteretic model for buckling and Steel02) and concrete (only unconfined).In order to compare the capacity of the rectangular and circular column in uniaxial and biaxial lateral loading,the pushover curves are presented in Fig.3 (a).Fig.3(b) shows the direction and axis of uniaxial and biaxial lateral loading.The drift ratio and base shear at x-axis and initiation of damage at each drift ratio are presented.The damage limits are calculated based on the material responses,such as steel yield strength and concrete crushing strength.Damage in RC sections generally starts with cracking and spalling of the cover concrete.Following spalling of the cover concrete,fracture of longitudinal reinforcing bars due to large tensile strain and/or low-cycle fatigue,crushing of the core confined concrete and/or buckling of longitudinal bars in compression may lead the structure to collapse.In this paper,damage states are calculated based on lateral force-deformation.Slight damage at 0.5% IDR is related to flexural or shear type hairline cracks.Moderate damage at 1% IDR corresponds to larger flexural cracks and some concrete spalling.Extensive damage at 3% IDR is related to large flexural cracks,spalled concrete and rebar buckling in columns (elements have reached their ultimate capacity).Finally,complete damage means that the column is collapsed or in imminent danger of collapse due to brittle failure or loss of stability.In general,it can be seen a reduction of 30% the lateral load-bearing capacity of the columns under biaxial loading in comparison to uniaxial loading.

Table 1:Details of the hypothetical columns

Column height (L),shear span to depth ratio (L/D),the ratio of effective buckling length of longitudinal bar to its diameter (Leff/d),the longitudinal bars ratio (ρl),volumetric ratio of transverse reinforcements (ρs),axial force ratio (Nu/fcAg) and fundamental period of each column (T1).

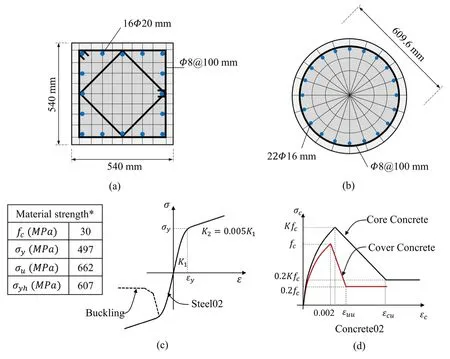
Figure 1:Cross section of RC column (a) rectangular,(b) circular,(c) material model for reinforcements and (d) material model for concrete,*fc is the measured strength of the concrete,based on tests of 150 mm by 300 mm cylinders,σy and σu are measured yield and ultimate strengths of the longitudinal reinforcement and σyh is the measured yield strength of the spiral reinforcement

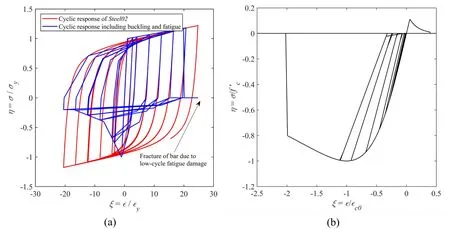
Figure 2:Cyclic response of the uniaxial material model used for fibers in columns,(a) conventional reinforcing material model (Steel02) and Hysteretic material model combined with Fatigue material model (Normalized by yield stress/strain),(b) normalized cyclic response of unconfined concrete for Concrete02 (Normalized by compressive strength/strain at maximum strength)

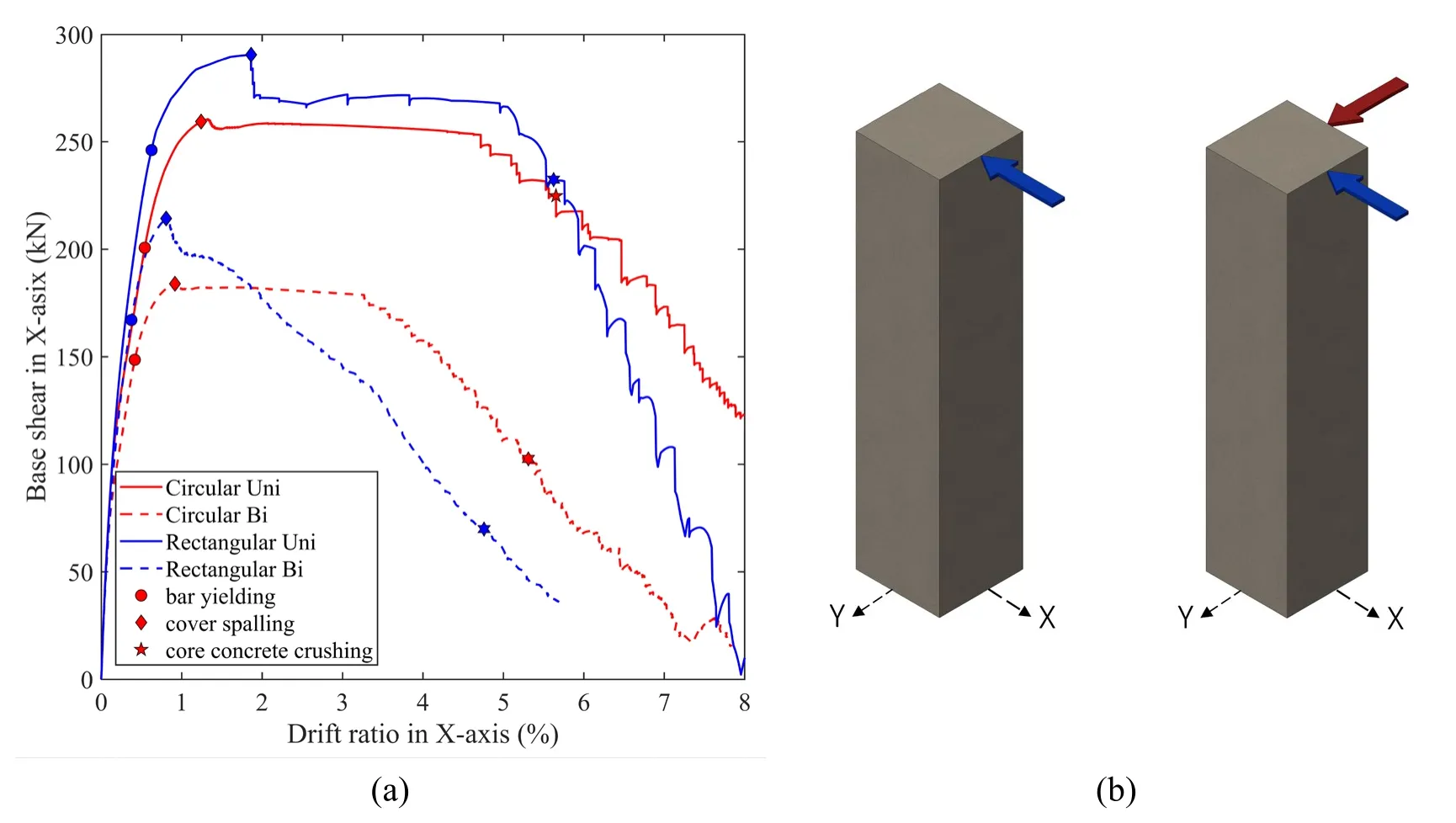
Figure 3:(a) Uniaxial and biaxial pushover curves for rectangular and circular column with different damage limits,(b) definition of uniaxial and biaxial pushover presented for rectangular column

3 Ground motion selection

The proposed column is located at a typical urban site in Los Angeles,US,(latitude/longitude=34.0522°N/118.2437°W).The site class is assumed to be of the NEHRP soil category D (Vs=259 m/s).Using the probabilistic seismic hazard analysis (PSHA) provided by USGS (https://www.usgs.gov/),the uniform hazard spectrum (UHS) and the 2% probability of exceedance in 50 years is presented in Fig.4(a).Knowing that the fundamental vibration period of the column is 0.2 s,and the annual frequency of exceedance of interest is 2% in 50 years,the Sa(T1) value is 2.2439 g.The ground motion prediction equations (GMPEs) associated with M=6.6,R=10 km,and ε=2.8 and the average predicted median spectrum are also presented in Fig.4(a).The information about the magnitude and distance for the specific site is presented in Fig.4(b).The disaggregation information for the specific site which shows the distribution of magnitudes,distance and their contribution to the site hazard is taken from USGS.In this paper,only the ground motions with a distance of less than 20 km are considered.Therefore,a single target response spectrum (CMS) is constructed using the average values of magnitude and distance as suggested by the USGS.CMS is considered in this paper as it provides the expected (i.e.,mean) response spectrum,conditioned on occurrence of a target spectral acceleration value at the period of interest.The CMS is a more appropriate target spectrum in comparison to UHS as the structural responses from ground motions matching the more probabilistically consistent CMS are thus significantly smaller than the responses from ground motions matching the UHS and having the same Sa(T1) level.For detail information about the method please refer to the Baker [Baker (2011)].

Due to the lack of locally recorded strong motion time-histories,ground motion data from other seismic regions are often required.To facilitate the record selection of appropriate MSAS sequences for seismic performance evaluation,real MSAS sequences that are constructed based on the PEER-NGA database for worldwide shallow crustal earthquakes [Goda and Taylor (2012)].MSAS sequences are referred to as real or as-recorded because no artificial method (such as randomized or back-to-back records) is used in generating MSAS records.In a sequence of ground motions,the record with the highest moment magnitude is the mainshock record and all other records are from aftershocks.In this study,only one major aftershock record is selected.172 sequences (each sequence consists of two horizontal components) are available from the PEER-NGA database.After defining the CMS for the specific location and structure of interest,the records can be selected to match the target spectrum.The geometric mean of both horizontal components is scaled to match the Sa(T1) which are presented in Fig.4(c).To prevent any sever artificialness in the MSAS sequences,the scaling is only implemented on the amplitude of the records.The frequency content and duration of records are kept as same as original records.The period range for this selection is based on the period range that the structural response of the structure is most sensitive.As suggested by Baker et al.[Baker and Cornell (2008)],the period range from 0.2T1 to 2.0T1 (0.04-0.4 s) is selected in this study for record selection.30 records have been selected and presented in Fig.4(d).Having the selected MSAS records corresponding the seismic hazard level at the site,IDA is used to calculate the capacity of the RC columns under biaxial multiple MSAS records.

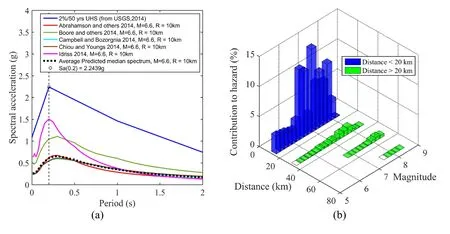
Figure 4:MSAs record selection,(a) UHS for Los Angles with GMPE,(b) disaggregation information from USGH,(c) conditional mean spectrum (CMS) with a geometric mean of all individual real MS records,(d) selected MS records for the specific structure and location

4 Results and discussion

The IDA results for mainshock-aftershock presented in this study are calculated by running time history simulations consist of MS record followed by 60 seconds of zero acceleration and then AS.By implementing this approach,the structural systems excited by previous ground motion return to at-rest condition (but might have sustained damage).A Matlab IDA algorithm runs the simulations for each scale of Sa(T1) and saves the maximum drift ratio for MS and MSAS.The following sections discuss the impact of aftershocks and structural modelling.

4.1 Impact of aftershocks

As mentioned before aftershocks have the potential of increasing the damage to RC structures.It was shown in previous studies [Salami,Kashani and Goda (2019)] that lowcycle fatigue damage index of RC elements increase under multiple excitation.The impact of aftershocks on rectangular and circular RC columns using the buckling model are presented in Fig.5.Two horizontal components (H1 and H2) are used simultaneously.The IDA results are presented separately for both drift directions.Damage levels of slight,moderate,extensive and complete damage corresponding to 0.05,1,3 and 5% lateral drift are also represented.Damage limits are defined based on the drift ratios following the biaxial pushover analysis.The MS and MSAS median IDA curve for the rectangular column are presented in Figs.5(a) and 5(b),while Figs.5(c) and 5(d) show the results for the circular column.It is evident that aftershock reduces the column capacity and this reduction is slightly more for the rectangular column.It is also noted that slight and moderate damage are not affected by aftershocks.Also,it is important to mention that there is not any remarkable difference in H1 and H2 components (drift inx-axisandyaxis),proving that in IDA assessment of structures if a sufficient number of records are used the direction of the records does not affect the output results.

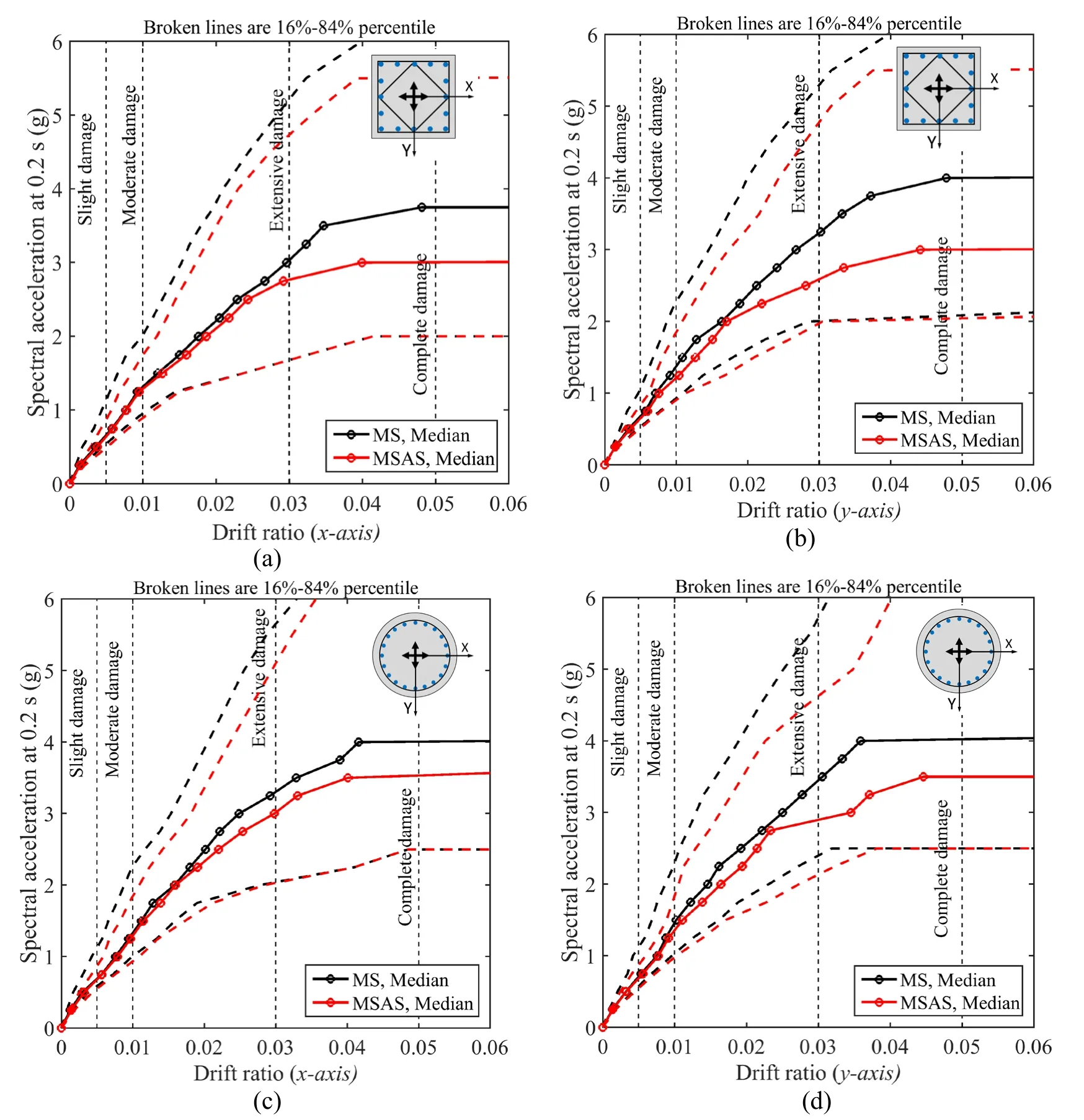
Figure 5:IDA results for MS and MSAS considering buckling and low-cycle fatigue,(a) rectangular column with x-axis drift,(b) rectangular column with y-axis drift (c) circular column with x-axis drift,and (d) circular column with y-axis drift

4.2 Impact of structural modeling

The impact of longitudinal rebar buckling on fragility curves of RC buildings has been investigated on Dizaj et al.[Dizaj,Madandoust and Kashani (2018);Salami,Kashani and Goda (2019)].It has been shown that the modeling technique significantly improves the accuracy of structural analysis of RC structures,especially at the collapse stage.Fig.6 presents the impact of structural modeling for rectangular and circular RC columns under biaxial multiple exactions.It can be seen that the capacity of the RC column is overestimated if buckling of longitudinal reinforcement is neglected by using conventional Steel02 material for steel fibers.It also reveals that the column with circular cross-section has slightly higher ductility and therefore more desirable performance under seismic excitation.Similar to the previous section,there is not a considerable difference between both H1 and H2 components (x-axisandy-axisdrift) of the ground motions used in this study.axis,and (d) circular column at y-axis

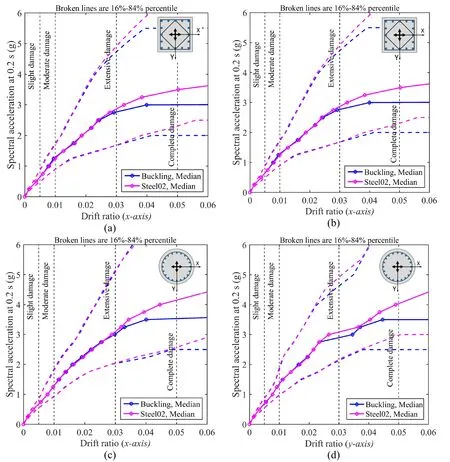
Figure 6:IDA results for buckling and Steel02 models under biaxial MSAS sequences,a) rectangular column at x-axis,(b) rectangular column at y-axis,(c) circular column at x-

4.3 Damage due to low-cycle fatigue

Considering the results in the previous section it is important to investigate the impact of low-cycle fatigue for the RC columns in detail.As it was mentioned in Section 2 and explained in detail in Kashani et al.[Kashani,Lowes,Crewe et al.(2016)],a generic Fatigue material model available in OpenSees is used to simulate low-cycle fatigue degradation of reinforcing bars.The Fatigue material uses a modified rainflow cycle counting algorithm to accumulate damage in a material using Miner’s rule [Ballio and Castiglioni (1995)].The material model can be wrapped to any steel model (or any other uniaxial materials) without changing the stress-strain state of the parent material.Once the fatigue damage index reaches to 1.0,the stress/strain of the parent steel material is assumed to become zero (damage index of 1 due to fatigue means fracture of reinforcement).

It is well-known that the aftershocks have the potential to increase damage [Raghunandan,Liel and Luco (2015);Salami,Kashani and Goda (2019)].In addition,the columns under biaxial loading are susceptible to having additional damage due to low-cycle fatigue [Hachem,Mahin and Moehle (2003)].Fig.7 presents the median fatigue damage index for rectangular and circular column under MS and MSAS records.In particular,Figs.7(a) and 7(b) show the median fatigue damage index under biaxial multiple excitations for rectangular and circular columns,respectively.The results are only presented for the corner longitudinal reinforcement (Northeast bar presented in red color).It is evident that aftershocks significantly increase the fatigue damage index of the longitudinal reinforcement for both rectangular and circular columns.In addition,Figs.7(c) and (d),present the median fatigue damage index for longitudinal reinforcement in the rectangular and circular column located at the corner,under biaxial MSAS.It can be seen that the bar in the rectangular column has a higher potential for failure due to low-cycle fatigue,which highlights the importance of the geometry of the section.A similar conclusion is achieved for the longitudinal reinforcement located in the opposite direction (at Southwest corner) of the RC column.

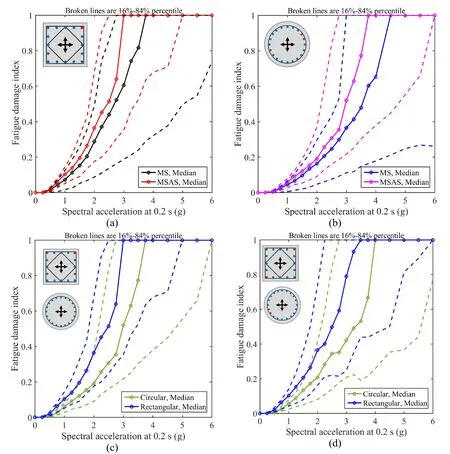
Figure 7:Fatigue damage index,(a) rectangular column,MS and MSAS fatigue damage index for Northeast bar,(b) circular column,MS and MSAS fatigue damage index for Northeast bar,(c) rectangular and circular fatigue damage index for MSAS and Northeast bar,(d) rectangular and circular fatigue damage index for MSAS and Southwest bar

5 Conclusion

In this paper,a combined effect of cross-sectional shape,biaxial loading and multiple excitations are investigated.Two rectangular and circular columns with equal stiffness and dynamic characteristics are used.An advanced structural modeling technique that can capture longitudinal rebar buckling and low-cyclic fatigue is implemented.In addition,a comprehensive ground motion selection is implemented to select real as-recorded mainshock-aftershock sequences.The main finding of this study is as follow:

• It is evident from the IDA results,that aftershocks have the potential to reduce the capacity of the columns.The slight and moderate damage levels are not affected by aftershocks.

• Rectangular columns are more sensitive and prone to damage in comparison to circular columns with similar dynamic characteristics,especially for the reinforcements located at the corners which are highly affected by biaxial loadings.

• In this preliminary study,single values for column height,reinforcement ratio,buckling length and axial load ratio have been considered,in the future research impact of variable parameters combined with different structural geometry will be investigated by developing fragility curves for each case.