OpenSees Three-Dimensional Computational Modeling of Ground-Structure Systems and Liquefaction Scenarios

Zhijian Qiu,Jinchi Lu,Ahmed Elgamal, ,Lei Su,Ning Wang and Abdullah Almutairi

Abstract:The OpenSees computational platform has allowed unprecedented opportunities for conducting seismic nonlinear soil-structure interaction simulations.On the geotechnical side,capabilities such as coupled solid-fluid formulations and nonlinear incrementalplasticity approaches allow for representation of the involved dynamic/seismic responses.This paper presents recent research that facilitated such endeavors in terms of response of ground-foundation-structure systems using advanced material modeling techniques and high-performance computing resources.Representative numerical results are shown for large-scale soil-structure systems,and ground modification liquefaction countermeasures.In addition,graphical user interface enabling tools for routine usage of such 3D simulation environments are presented,as an important element in support of wider adoption and practical applications.In this context,Performance-Based Earthquake Engineering (PBEE) analysis of bridge-ground systems is highlighted as an important topical application.

Keywords: Numerical simulation,OpenSees,geotechnical,earthquake,soil liquefaction,seismic response.

1 Introduction

With the recent developments in material modeling techniques and high-speed computing,three-dimensional (3D) nonlinear Finite Element (FE) simulations are becoming increasingly feasible for geotechnical earthquake engineering applications [Elgamal,Yan,Yang et al.(2008);Kwon and Elnashai (2008);Asgari,Oliaei and Bagheri (2013);Torabi and Rayhani (2014);McGann and Arduino (2014,2015);Rayamajhi,Nguyen,Ashford et al.(2013);Rayamajhi,Ashford,Boulanger et al.(2016a);Rayamajhi,Boulanger,Ashford et al.(2016b);Su,Lu,Elgamal et al.(2017)].Calibration,on the basis of data from field case histories as well as centrifuge and shake table experiments,is gradually allowing for more accurate computational modeling efforts [Lu,Elgamal,Yan et al.(2011);Chang,Boulanger,Brandenberg et al.(2013);Karimi and Dashti (2015,2016);He,Ramirez,Lu et al.(2017);Su,Wan,Li et al.(2018)].As such,calibrated FE simulations are increasingly providing a reliable environment for modeling geotechnical earthquake problems,such as soil liquefaction,soil-structure interaction (SSI),and ground modification.

Particularly suited to seismic applications,the open-source computational platform OpenSees [Mazzoni,McKenna and Fenves (2006);McKenna (2011)] provides such 3D simulation capabilities.Implemented in OpenSees [Yang (2000);Yang and Elgamal (2002)] is an analysis framework for saturated soil response as a two-phase material following theu-pformulation of Chan (1988) and Zienkiewicz et al.(1990) [Chan (1988);Zienkiewicz,Chan,Pastor et al.(1990)],whereuis displacement of the soil skeleton,andpis pore pressure.As such,the soil domain (in 3D) is represented by effective-stress solidfluid fully coupled brick elements [Parra (1996);Yang (2000);Lu (2006);Yang,Lu and Elgamal (2008)] to describe the solid translational degrees of freedom (DOFs) and the fluid pressure (e.g.,OpenSees 20_8_BrickUPelement,brickUP and bbarBrickUP elements).

The OpenSees framework also includes a number of pressure-independent and pressuredependent soil constitutive models [Parra (1996);Yang and Elgamal (2002);Elgamal,Yang,Parra et al.(2003);Yang,Elgamal and Parra (2003);Yang,Lu and Elgamal (2008)],developed based on the multi-surface-plasticity theory [Mroz (1967);Iwan (1967);Prevost (1977,1978,1985)].The pressure-independent models [Elgamal (2008);Yang,Lu and Elgamal (2008);Lu,Elgamal,Yan et al.(2011)] simulate the nonlinear cyclic hysteresis material response (e.g.,undrained clay-type loading conditions).The pressure-dependent material models (typically used with the above mentioned solid-fluid fully coupled brick elements) mainly aim at simulating the liquefaction-induced shear strain accumulation mechanism in cohesionless soils [Yang and Elgamal (2002);Elgamal,Yang,Parra et al.(2003);Yang,Elgamal and Parra (2003);Yang,Lu and Elgamal (2008)].Currently,the above modeling tools have been used by the co-authors and researchers worldwide in numerous reported studies [Elgamal,Yan,Yang et al.(2008);Elgamal,Lu and Forcellini (2009);Zhang,Conte,Yang et al.(2008);Kwon and Elnashai (2008);Aygün,Dueñas-Osorio,Padgett et al.(2009,2010);Ilankatharan and Kutter (2008,2010);Atik and Sitar (2010);Lu,Elgamal,Yan et al.(2011);Asgari et al.2013;Chang,Boulanger,Brandenberg et al.(2013);Torabi and Rayhani (2014);McGann and Arduino (2014,2015);Hashash,Dashti,Romero et al.(2015);Tang,Cong,Ling et al.(2015);Rayamajhi,Nguyen,Ashford et al.(2013);Rayamajhi,Ashford,Boulanger et al.(2016a);Rayamajhi,Boulanger,Ashford et al.(2016b);Karimi and Dashti (2015,2016);He,Ramirez,Lu et al.(2017);Su,Lu,Elgamal et al.(2017);Su,Wan,Li et al.(2018)].

In order to facilitate the OpenSees analysis pre- and post-processing phases,the graphical user interfaces OpenSeesPL [Lu,Yang and Elgamal (2006);Elgamal and Lu 2009)],BridgePBEE [Mackie,Lu and Elgamal (2012)] and MSBridge [Elgamal,Lu and Mackie (2014)] were developed and employed.OpenSeesPL allows for execution of push-over and seismic SSI pile-ground simulations [Lu,Yang and Elgamal (2006);Elgamal and Lu (2009)].In addition,various ground modification scenarios may be studied in OpenSeesPL by appropriate specification of the material within the pile zone.BridgePBEE is a userinterface for conducting performance-based earthquake engineering (PBEE) studies for 2-span single-column bridge-ground systems [Mackie,Lu and Elgamal (2012)].MSBridge focuses on efficiently conducting nonlinear FE studies for a wide range of multi-span bridge systems [Elgamal,Lu and Mackie (2014)],with a recently added PBEE analysis option [Elgamal,Lu,Almutairi et al.(2017);Almutairi,Lu,Elgamal et al.(2018)].

To illustrate the above analysis components,this paper presents representative ground and ground-structure studies including a large-scale pile group,a ground-bridge system,a pilesupported wharf,a stone-column liquefaction countermeasure,and bridge PBEE analysis applications.In the following sections,the pressure-independent and pressure-dependent soil constitutive models are briefly described,followed by the above-mentioned representative computational studies.Salient characteristics of the soil models are highlighted,and key results of the numerical studies are presented.

2 Soil constitutive models

The pressure-independent models exhibit plasticity in the deviatoric response and the volumetric response is linear-elastic,independent of the deviatoric response.The related OpenSees materials include PressureIndependMultiyield [Elgamal,Yan,Yang et al.(2008);Lu,Elgamal,Yan et al.(2011)] and PressureIndependMultiyieldSoftening [Qiu (2020)].

The pressure-dependent material models simulate the essential characteristics of pressure sensitive soil response under general loading conditions.As such,soil is simulated by the implemented OpenSees materials PressureDependMultiYield [Parra (1996);Yang (2000);Yang and Elgamal (2002);Elgamal,Yang,Parra et al.(2003)],PressureDependMultiYield02 [Yang,Elgamal and Parra et al.(2003)],PressureDependMultiYield03 [Khosravifar,Elgamal,Lu et al.(2018)],and LadeDuncanMultiYield [Yang and Elgamal (2008);Qiu (2020)].

2.1 PressureIndependMultiYieldSoftening material

Based on the existing multi-yield surfaceJ2associative plasticity formulation [Prevost (1977);Elgamal,Yan,Yang et al.(2008);Lu,Elgamal,Yan et al.(2011)],the PressureIndependMultiYield material (Fig.1) has been implemented in OpenSees for simulating elasto-plastic undrained clay-type shear response.In this model,a hyperbolic backbone curvecan be employed to describe the backbone shear stressstrain curve (Fig.1(b)),whereGis the low-strain shear modulus,τandγdenote the octahedral shear stress and shear strain,respectively,andγris the reference shear strain (computed as),in whichτmaxis the peak shear strength that corresponds to the shear strainγmax).Alternatively,conventional shear modulus reduction (G/Gmax) curves may be conveniently employed for the specification of yield surfaces and their characteristics.Further details and model implementation specifics can be found in Prevost [Prevost (1977)] and Gu et al.[Gu,Conte,Elgamal et al.(2009);Gu,Conte,Yang et al.(2011);Gu,Qiu and Huang (2015)].

Figure 1:PressureIndependMultiYield material [Elgamal,Yan,Yang et al.(2008);Lu,Elgamal,Yan et al.(2011)]

Extending the PressureIndependMultiYield material with a newly developed strain softening logic,a PressureIndependMultiYieldSoftening material was recently developed and calibrated based on a series of laboratory sample test data [Qiu (2020)].For this model,Fig.2(a) presents a range of response scenarios that can be generated by the incorporated softening logic [Qiu (2020)].As such,representation of strain softening is an important consideration for a wide range of ground formations involving sensitive clays,cemented soils,over-consolidated soils,very dense soils,or frozen soils among others.Fig.2(b) depicts the model response under cyclic loading with an imposed static shear stress bias.As can be seen in Fig.2(b),the model reproduces the downslope cycle-by-cycle accumulation of shear deformations and the degradation of shear stiffness and strength.

Figure 2:Model simulation of PressureIndependMultiYieldSoftening material [Qiu (2020)]:(a) Monotonic loading;(b) Cyclic loading with static shear stress bias

2.2 PressureDependMultiYield03 material

The PressureDependMultiYield02 material (Fig.3) has mechanisms to simulate the dilatancy and cyclic mobility of pressure sensitive soils [Elgamal,Yang,Parra et al.(2003);Yang,Elgamal and Parra et al.(2003)].Calibration was performed based on a series of laboratory and centrifuge tests,and the model parameters were provided for sands with different relative densities.Representative simulation results using the PressureDependMultiYield02 material for a symmetric stress-controlled cyclic shear loading test are shown in Fig.3(b).A large number of numerical studies employing the OpenSees PressureDependMultiYield02 material have been conducted for simulating large-scale seismic soil-structure interaction and liquefaction scenarios [Shin,Arduino and Kramer (2007);Shin,Arduino,Kramer et al.(2008);Zhang,Conte,Yang et al.(2008);McGann and Arduino (2014,2015);Karimi and Dashti (2015);He,Ramirez,Lu et al.(2017);Su,Wan,Li et al.(2018)].

Figure 3:PressureDependMultiYield02 material [Yang,Elgamal and Parra et al.(2003)]:(a) Yield surfaces;(b) Model response under stress-controlled,undrained cyclic shear loading

In order to more closely capture the established guidelines concerning triggering of liquefaction [Idriss and Boulanger (2008)],the PressureDependMultiYield02 material has been recently updated (PressureDependMultiYield03 in Khosravifar et al.[Khosravifar,Elgamal,Lu et al.(2018)].Fig.4 depicts the calibration results of PressureDependMultiYield03 for direct simple shear loading tests with a vertical consolidation stress of 1 atm and lateral earth pressure coefficientsKo=0.5 (Fig.4(a)) andKo=1.0 (Fig.4(b)),along with those of the PM4Sand model [Boulanger and Ziotopoulou (2015)] response for comparison.

Figure 4:Calibration of Pressure Depend Multi Yield03 material [Khosravifar,Elgamal,Lu et al.(2018)]:(a) Lateral earth pressure coefficient Ko=0.5;(a) Ko=1.0

2.3 LadeDuncanMultiYield mat eri al

To allow for further accuracy in capturing 3D shear response,the PressureDependMultiYield03 material has been extended to incorporate the Lode angle effect (Fig.5(a)) by employing the Lade-Duncan failure criterion as the yield function [Lade and Duncan (1975);Yang and Elgamal (2008);Qiu (2020)].This failure criterion is represented by Chen et al.[Chen and Mizuno (1990)]:

where,I1is volumetric stress,J2andJ3are second and third deviatoric stress invariants,r espectively,parameterk1(＞27) is related to soil shear strength (or friction angleφ).A typical yield surfacefm(Fig.5(a)) is defined by Yang et al.[Yang and Elgamal (2008)]:

whereηmis a normalized yield surface size (0＜ηm＜1) and material parameter[Yang and Elgamal (2008)].In Eq.(2),andwhere,is the deviatoric stress tensor,is mean effective stress (I1= 3p′),I2is 2ndunit tensor,deviatoric tensor a is back stress (yield surface center),and the operators “·”and “:” denote single and double contraction of two tensors,respectively.

Figure 5:LadeDuncanMultiYield material [Yang and Elgamal (2008);Qiu (2020)]:(a) Configuration in principal stress space;(b) Experimental and computed results [Hatanaka,Uchida and Ohara (1997);Qiu (2020)]

For illustration,the LadeDuncanMultiYield material was calibrated using laboratory cyclic undrained stress-controlled test data of a reclaimed gravely fill Masado soil [Hatanaka,Uchida and Ohara (1997)].It can be seen that the soil gradually loses its effective confinement during cyclic triaxial loading,and the axial strain accumulates on a cycle-bycycle basis (Fig.5(b)) after liquefaction,with a strong dilative tendency.It is noted that this LadeDuncanMultiYield material was recently updated [Qiu (2020)] to include the liquefaction triggering logic proposed by Idriss et al.[Idriss and Boulanger (2008)].

3 Large-scale numerical modeling of 3D soil-structure interaction

Seismic response of structures is dictated by soil-structure interaction (SSI) during earthquake loadings.To reproduce such SSI effects computationally,a large domain of the soil surrounding the structure is often necessary to be modeled [Chae,Ugai and Wakai (2004);Maheshwari,Truman,El Naggar et al.(2004);Elgamal,Yan,Yang et al.(2008);Elgamal,Lu and Forcellini (2009);Elgamal and Lu (2009);Wang,Lu and Elgamal et al.(2013);Chiaramonte,Arduino,Lehman et al.(2013);Su,Lu,Elgamal et al.(2017);Qiu (2020)].

3.1 Bridge-ground seismic response

Damage to large bridge overcrossings has been observed in recent earthquakes,including 2010 Maule [Arduino,Ashford,Assimaki et al.(2010)] and 2011 Christchurch [Cubrinovski,Bradley,Wotherspoon et al.(2011);Cubrinovski (2013)].The observed response was often noted to be highly influenced by the global bridge-ground overall characteristics as an integral system.

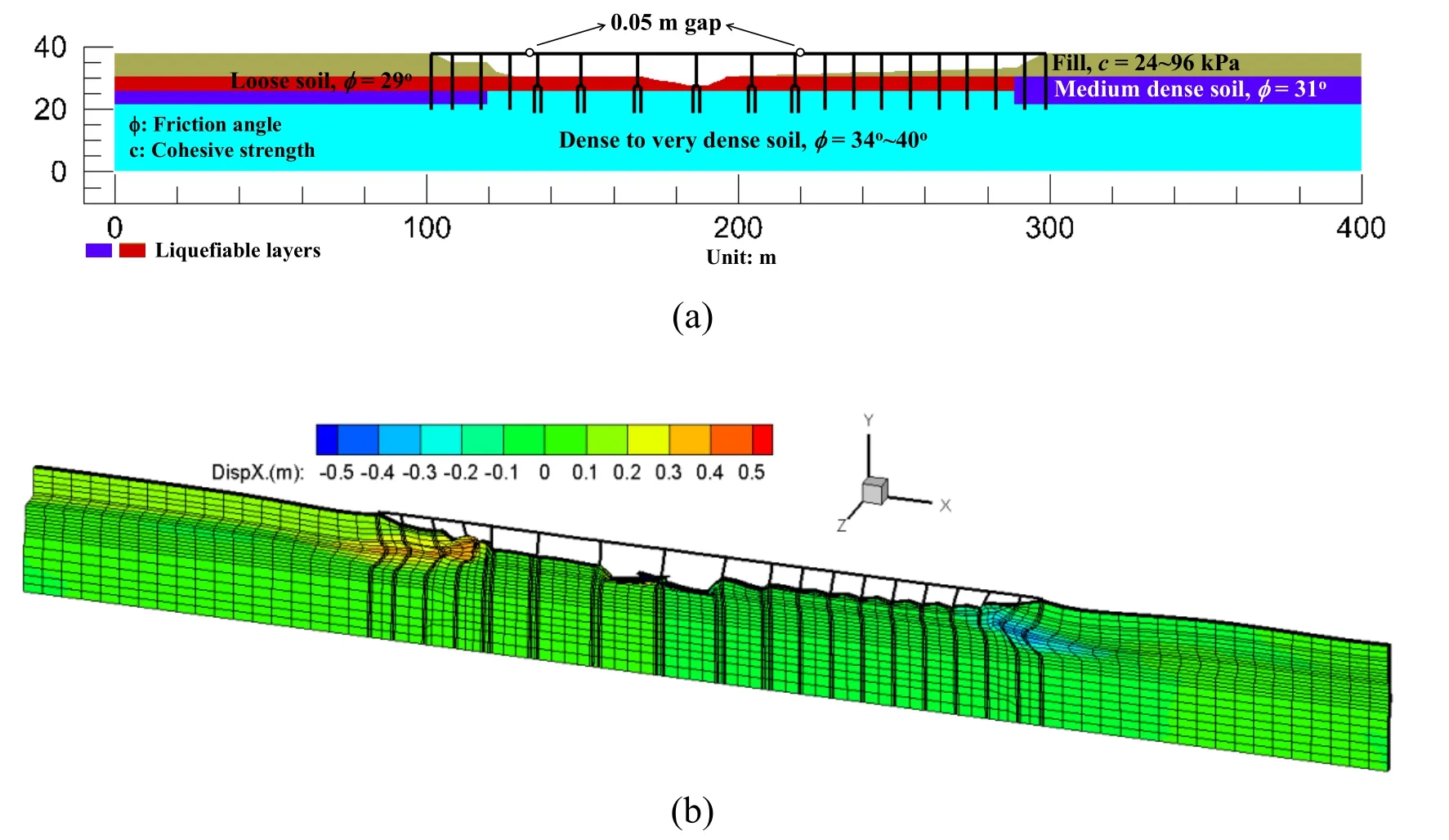
Figure 6:A bridge-ground system [Qiu (2020)]:(a) Ground configuration;(b) Deformed mesh at the end of shaking (factor=15)

On this basis,a representative 3D FE model underlain by liquefiable soil was developed to numerically investigate the consequences of liquefaction-induced ground deformation [Qiu (2020)].The overall ground configuration is shown in Fig.6(a).In general,the site soil profile consists of shallow,fine-grained soils underlain by medium dense to dense sands,with loose sand layers (red zone in Fig.6(a)).Water table was prescribed at the elevation of 30.5 m.The 18-span reinforced concrete bridge is approximately 197 m long and 9.9 m wide,composed of a reinforced concrete deck on vertical pier walls with pile groups and/or single piles.Two expansion joints (with a 0.05 m gap each,Fig.6(a)) are located adjacent to the piers.In the transverse direction,a 1.83 m wide 3D slice was taken as a representative of the bridge’s geometric configuration.As such,the FE model of actual 3D geometric pile layout was presented,with the mesh composed of 17,415 brick elements.

Along both side mesh boundaries,2D plane strain soil columns of large size and depth (not shown) are included to minimize boundary effects,efficiently reproduce the desired freefield site response at these locations [Su,Lu,Elgamal et al.(2017)].Along the FE model base,the Lysmer-Kuhlemeyer absorbing boundary [Lysmer and Kuhlemeyer (1969)] was applied.Input motion was selected as that of the 1940 Imperial Valley earthquake at El Centro Station (Component S00E),scaled to a peak acceleration of about 0.4 g.Using this excitation,via deconvolution by Shake91 [Idriss and Sun (1993)],an incident earthquake motion was derived and imparted [Elgamal,Yan,Yang et al.(2008)] in the x-direction (i.e.,input shaking only in the longitudinal direction),along the base of the FE model (elevation 0.0 in Fig.6(a)).

Fig.6(b) displays the deformed FE mesh at the end of shaking (colors show horizontal displacement).Away from the bridge,lateral deformation above the liquefied strata was to the right,about 0.2 m on the left-side and only 0.008 m on the right-side.Superposed on this global displacement pattern (to the right),local downslope deformations are seen at both ends of the bridge (Fig.6(b)).Near the abutments,additional downslope deformation relative to the surrounding ground was about 0.35 m (left-side),and 0.4 m (right-side).Due to the downslope deformations at both ends,expansion joint gaps were closed,with the bridge deck through its piers and foundations acting as a strut that provides added restraint to the slope deformations.

3.2 Pile-supported wharf seismic response and OpenSeesMP

Seaports are among the large-scale constructed facilities that are particularly vulnerable to damage and loss of function due to seismic activities [Akai,Bray,Christian et al.(1997);Mahoney,Francis and Kennard (2008);Percher,Bruin,Dickenson et al.(2013);Edge,Eskijian and Arulmoli (2013)].The observed seismic performance of pile-supported wharves is significantly dictated by the behavior of the surrounding soil.

To address this consideration,a ground-structure 3D FE model was developed [Su,Lu,Elgamal et al.(2017)] to capture and further elucidate many salient characteristics,such as pile-to-pile and pile-ground interaction mechanisms.On this basis,a representative 6.3 m wide 3D slice of a wharf-ground configuration (Fig.7(a)) was presented [EMI (2001);Su,Lu,Elgamal et al.(2017)].

As such,the FE mesh of this pile-supported wharf included 9,649 3D brick elements (Fig.7(a)).The input motion was selected as 1994 Northridge earthquake (Component S48W) at the Rinaldi Receiving Station,scaled down to half amplitude [Su,Lu,Elgamal et al.(2017)].Along both side mesh boundaries,2D plane strain soil columns of large size and depth (not shown) are included to minimize boundary effects (Fig.7(a)),efficiently reproduce the desired free-field site response at these locations [Su,Lu,Elgamal et al.(2017)].

Figure 7:A pile-supported wharf [Su,Lu,Elgamal et al.(2017)],with total mesh length of 230 m,width of 6.1 m,height (landside) of 53.8 m and height (waterside) of 33.5 m:(a) FE mesh partitioning for parallel computation (different colors represents partitioned zones for different processors);(b) Deformed mesh (scale factor=20)

A parallel version of OpenSees (OpenSeesMP) was employed to conduct the 3D simulations of this wharf-ground configuration (Fig.7(a)).OpenSeesMP was created for running input scripts with user-specified subdomains,parallel equation solver and parallel numberer [McKenna (2011)].As seen in Fig.7(a),the FE mesh of the pile-supported wharf model was divided into three zones (handled simultaneously by three different processors).With the computations conducted in parallel (implicit time integration),execution time was reduced by more than 50% [Lu,Peng,Elgamal et al.(2004)].

Fig.7(b) displays the deformed mesh at maximum deck displacement.In this figure,the largest lateral displacements showed in the upper layers,mainly due to the shear deformation in the relatively weak clay stratum (Fig.7(a)).Away from the slope,lateral deformation on the landside above the clay was about 0.25 m towards the waterside.Superposed on this landside displacement pattern,local downslope deformation is seen in the slope zone (Fig.7(b)),reaching a peak value of about 0.45 m relative to the surrounding ground.

4 OpenSeesPL,ground modification,and pile/pile group analyses

A PC-based graphical pre- and post-processor (user interface) OpenSeesPL has been developed to facilitate efficient execution of 3D ground-foundation FE simulations [Lu (2006);Lu,Yang and Elgamal (2006);Elgamal and Lu (2009)];http://www.soilquake.net/openseespl/) [Lu (2006);Lu,Yang and Elgamal (2006);Elgamal and Lu (2009)].Currently,OpenSeesPL permits analyses of footings,piles and pile groups (Fig.8) under static and earthquake loading conditions [Wang,Lu and Elgamal et al.(2013)].Various scenarios of ground modification can be also studied by specifying the material within the pile zone [Elgamal,Lu and Forcellini (2009);Asgari,Oliaei and Bagheri (2013);Tang,Cong,Ling et al.(2015);Rayamajhi,Nguyen,Ashford et al.(2013);Rayamajhi,Ashford,Boulanger et al.(2016a);Rayamajhi,Boulanger,Ashford et al.(2016b)].FE computations in OpenSeesPL are conducted using OpenSees.

Figure 8:Pre- and postprocessor graphical interface OpenSeesPL [Lu (2006)]:(a) FE mesh showing a 8×7 pile group (half mesh configuration because of symmetry);(b) Deformed mesh of the pile group under lateral loading

OpenSeesPL includes options for (1) defining the pile geometry (circular or square pile) and soil material properties (linearly elastic or nonlinear),(2) defining the 3D spatial soil domain,(3) defining the boundary conditions and ground input excitation or push-over analysis parameters,and (4) selecting soil materials from an available menu of cohesive and cohesionless soil materials.The menu of soil materials includes a complementary set of soil modeling parameters representing soft,medium,and stiff cohesive soils,and loose,medium,and dense cohesionless soils (with gravel,sand,or silt permeability).OpenSeesPL also allows convenient postprocessing and graphical visualization of the FE analysis results including ground response time histories,pile responses (profiles and time histories),and the deformed mesh (Fig.8(b)).The user interface makes it possible for users to quickly build a FE model,run the FE analysis,and evaluate the performance of the groundfoundation system [Lu,Yang and Elgamal (2006)].Representative studies employing OpenSeesPL are presented below.

4.1 Stone column mitigation of liquefaction-induced lateral ground deformations

Liquefaction-induced lateral spreading may result in disruption of function,significant damage,and considerable replacement cost for existing foundations,buildings,and structures.This type of adverse response has been observed in many earthquakes,such as Niigata,Japan 1964 [Seed and Idriss (1967)],Chi-Chi,Taiwan 1999 [EERI (2000)],Kocaeli,Turkey 1999 [EERI (2001)] and Christchurch,New Zealand 2011 [Cubrinovski,Bradley,Wotherspoon et al.(2011);Cubrinovski (2013)].The risk of liquefaction and associated ground deformation may be reduced by ground improvement approaches including solidification (cementation),densification,and gravel drains or stone columns (SCs).Use of gravel drains/SCs is a relatively recent development compared with more traditional soil remediation approaches [Elgamal,Lu and Forcellini (2009)].

4.1.1 Mitigation by stone columns

Using OpenSeesPL,a mildly inclined 4° saturated sand layer of 10 m thickness was studied (permeabilityk=6.6×10-5m/s),based on Nevada sand properties at a relative densityDrof about 40% [Yang,Elgamal and Parra et al.(2003);Elgamal,Yang,Parra et al.(2003);Elgamal,Lu and Forcellini (2009)].Dense sand properties with a representative gravel permeabilityk=1.0×10-2m/s were employed to represent the SC properties.In the remediated cases,the area replacement ratiois conventionally defined as t he ratio of the SC areaArover the tributary areaA(Fig.9(a)),whered=diameter of the SC,ands=distance (spacing) between SC centers.

Figure 9:Mitigation of liquefaction-induced lateral deformation in a sloping stratum (blue zone represents remediated domain;Elgamal et al.(2009)) [Elgamal,Lu and Forcellini (2009)]:(a) FE mesh (created in OpenSeesPL);(b) Ground surface lateral displacement response time histories (for 10%-50% Arr SC cases,along with remediated Medium Sand case for comparison) and base input motion

Diameter of the SC in all remediated cases was kept at 0.6 m.A total of five simulations were conducted to exploreArrvalues from 10% up to 50% with base input motion being that recorded at the Wildlife site during the 1987 Superstition Hills earthquake [Elgamal,Lu and Forcellini (2009)].The medium sand case (MS) represents the original benchmark unremediated scenario.As such,the MS results provide a reference of free-field site response for comparing with the remaining SC remediated cases (Fig.9(b)).When the SC permeabilityk=1.0×10-2m/s,the permanent displacement at the ground surface fell below the large displacement range (0.3 m or 1 ft according to Youd 1989 forArr=20%-30%) [Youd (1989)].To achieve a lower permanent displacement [CGS (2008)],anArr=40% is required.

4.1.2 Influence of stone column spatial distribution

In order to explore influence of SC spatial distribution on liquefaction-induced lateral deformation,a number of SC configurations (1×1,2×2 and 4×4) for a givenArr=10% were studied (Fig.10(a)).In these configurations [Lu,Kamatchi and Elgamal (2019)],the sameArris maintained by deploying smaller diameter columns,evenly distributed spatially,so as to increasingly reduce the drainage path (Fig.10(b)).On this basis,a total of seven simulations were performed exploring different combinations of SC geometric configurations and permeabilities.As mentioned above,the MS (unremediated) case represents the original benchmark situation to provide a reference of free-field site response for comparing with the remaining remediated cases.

Figs.10(c) and 10(d) show the lateral displacement time histories at the ground surface.Permanent ground surface displacement for the unremediated case is 1.15 m.A major reduction in ground deformation resulted because of the increased SC permeability.The more evenly distributed (or smaller-diameter) SC configuration (e.g.,the 2×2 pattern compared to the 1×1,or the 4×4 compared to the 2×2) is seen to be more effective in reducing the lateral deformation of the sand stratum (Figs.10(c) and 10(d)).As mentioned above,this is mainly attributed to the shorter drainage path in the smaller-diameter configurations.With a higher SC permeabilityk=0.1 m/s,permanent ground surface deformation falls below the large displacement range (0.3 or 1 ft m according to Youd 1989) [Youd (1989)],with substantial reductions in the 2×2 and 4×4 configurations compared to the 1×1 scenario [Lu,Kamatchi and Elgamal (2019)].

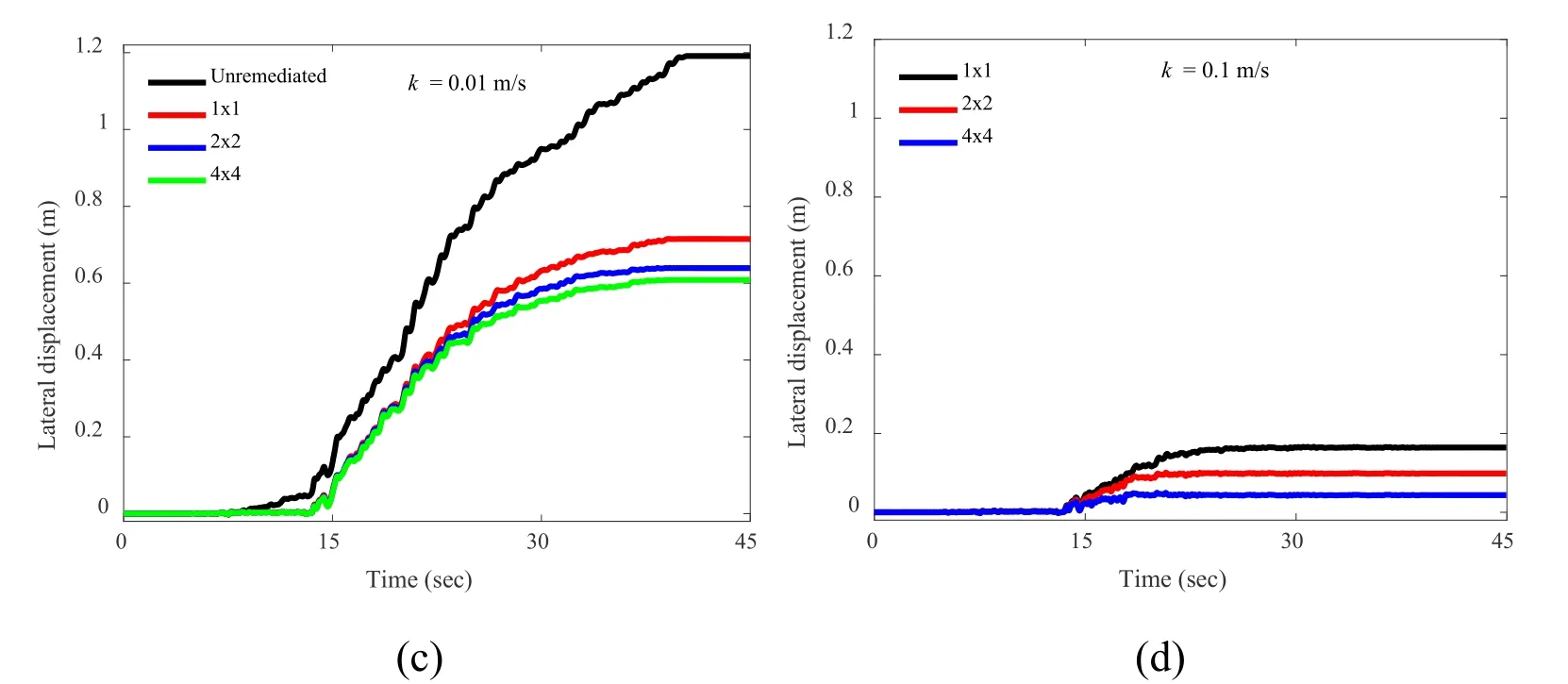
Figure 10:Ground modification study of drainage effect (blue zone represents remediated domain [Lu,Kamatchi and Elgamal (2019)]:(a) FE mesh (created in OpenSeesPL);(b) 1×1,2×2,and 4×4 SC configurations showing reduction in the radial drainage path;(c) and (d) Ground surface lateral displacement response time histories for permeability k=0.01 m/s,and k=0.1 m/s,respectively

4.2 Lateral load on a large pile group

Using OpenSeesPL,a systematic 3D FE study of a large pile group subjected to lateral loading was performed (Figs.11(a) and 11(b)).The FE model was representative of the Dumbarton Bridge (California) Pier 23 pile-group foundation geometry [Wang,Lu and Elgamal et al.(2013);Wang (2015)].The pile group is configured in an 8×4 arrangement with a longitudinal spacing of 2 pile diameters and a transversal spacing of 2.15 pile diameters on center.The diameter and length for each pile were 1.37 m and 30.8 m,respectively.The group is rigidly connected by a pile cap,at a substantial distance of 14.3 m above the mudline.

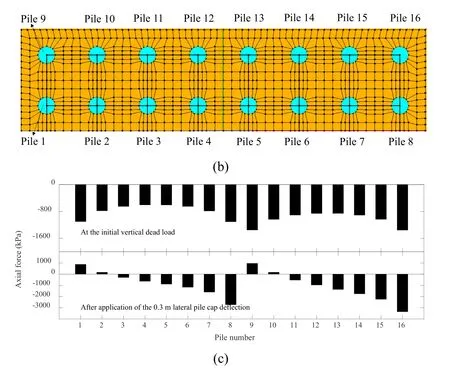
Figure 11:A large pile group subjected to lateral loading [Wang,Lu and Elgamal et al.(2013)]:(a) Close-up of FE mesh (created in OpenSeesPL);(b) Layout of pile group;(c) Axial forces,initial,and at 0.3 m pile cap deflection

The pile response was assumed to be linear elastic and the bending stiffness for each pile wasEI=2×106kN-m2[Wang,Lu and Elgamal (2013)].A summary of the site soil profile is reported in Wang (2015) [Wang (2015)].In the employed OpenSeesPL half mesh of Fig.11 (due to symmetry),the vertical dead load (28,900 kN representing the tributary own weight of the bridge deck.) was imposed initially (after application of soil own weight).A lateral pile cap longitudinal displacement was then applied (at the center of the pile cap) up to a maximum of 0.30 m.

Fig.11(c) shows the axial force distribution between piles (1-16).In this figure,a wide range in the share of load is seen in each pile.At the initial static state,the corner piles (1,8,9 and 16) carry the highest force.At the 0.3 m pile cap displacement,the compressive axial forces of front piles (6-8 and 14-16) increase significantly,conversely the back piles (1,2 and 9,10) experience tensile forces.Such variation in axial forces is influenced by the relatively large distance between the pile cap and the mudline,exerting a significant moment on the overall pile foundation along with the pile lateral forces.

5 Performance-based earthquake engineering (PBEE) for bridge systems and MSBridge

PBEE aims to quantify the seismic performance of engineered facilities,such as bridges,using metrics that are compatible with network risk assessment and of interest to engineers and stakeholders alike [Mackie,Lu and Elgamal (2012)].Using a fully developed bridge PBEE assessment framework [Mackie,Lu and Elgamal (2012)],a pre- and post-processor user interface (Fig.12) was developed for application within the simple environment of a 2 span,single column bridge founded on a 3D ground soil mesh.This interface (https://peer.berkeley.edu/bridgepbee/) integrates all elements of the underlying FE simulations along with the subsequent PBEE calculations [Mackie,Lu and Elgamal (2012)].In the time history analysis phase,the bridge column is modeled by nonlinear fiber section beam-column elements.Abutment models considering passive soil resistance,bearing pads,and shear keys are included.If a computation cluster is available,a parallel version of OpenSees (OpenSeesSP) can be used to efficiently complete all individual shaking event simulations simultaneously (Fig.13),in a couple of hours versus a couple of days for instance.

Figure 12:Pre- and postprocessor graphical interface BridgePBEE [Mackie,Lu and Elgamal (2012)]:(a) FE mesh of a bridge-ground system (2-span single-column type);(b) Deformed mesh (scale factor=50) of the bridge-ground model under lateral loading

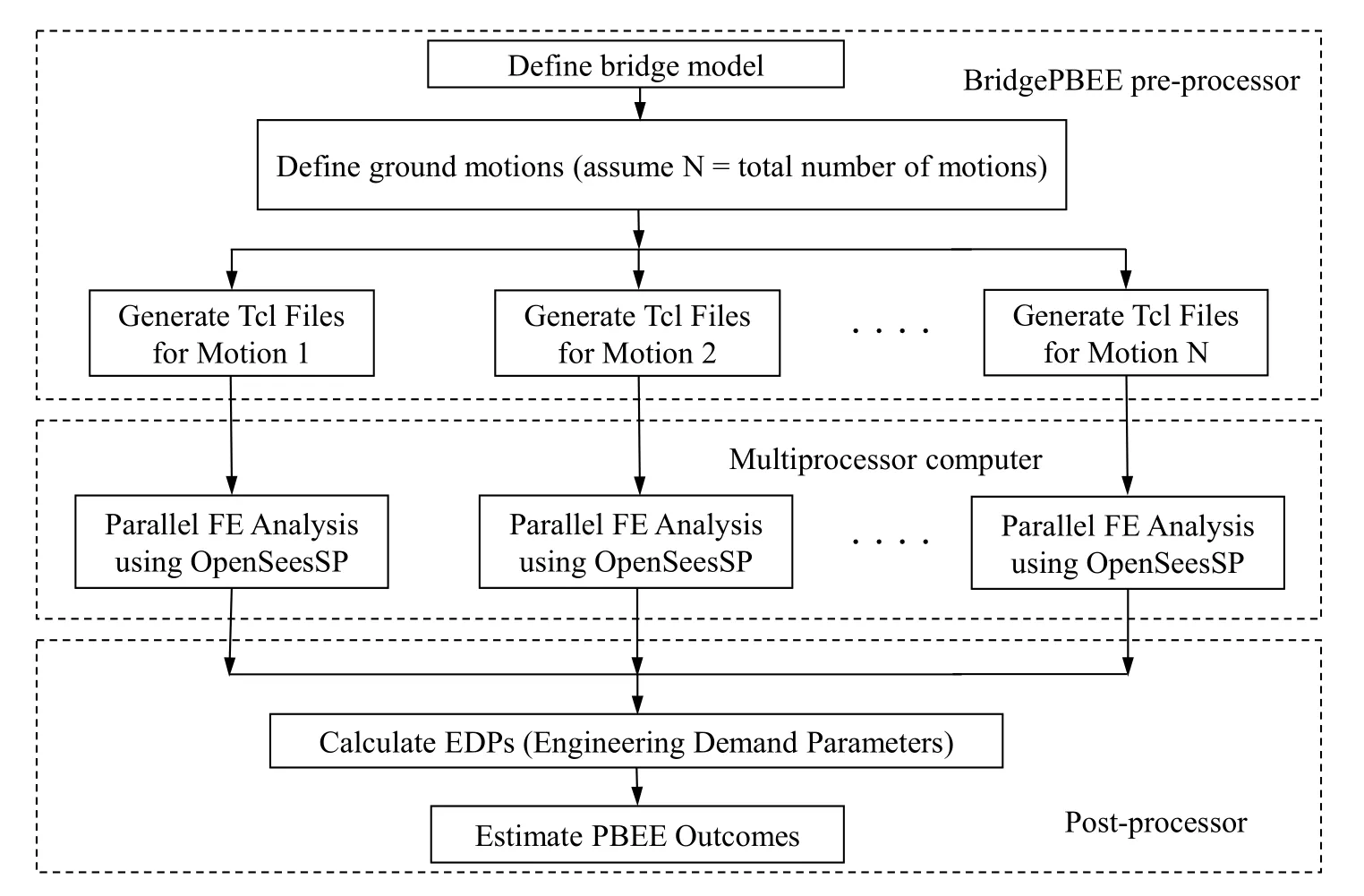
Figure 13:Parallel computation in BridgePBEE

The bridge-foundation-ground mesh is shown in Fig.14(a) for illustration.Response of the same bridge is explored under stiff and soft supporting soil conditions [Mackie,Lu and Elgamal (2012)].Fig.14(b) shows the corresponding mean repair cost ratio (RCR) loss models.The consequences of shaking and repair do not begin to accumulate until a PGV of approximately 20 cm/s is reached,and repair costs are clearly higher for the soft soil scenario.Building on the above developments,systematic PBEE analyses were recently implemented for multi-span reinforced concrete bridges [Almutairi,Lu,Elgamal et al.(2018)].In this regard,the bridge seismic response is handled by the new highly versatile pre- and post-processor graphical user interface MSBridge [Elgamal,Lu,Almutairi et al.(2017);Almutairi,Lu,Elgamal et al.(2018)],http://www.soilquake.net/msbridge/) [Elgamal,Lu,Almutairi et al.(2017);Almutairi,Lu,Elgamal et al.(2018)].Using OpenSees,this interface is focused on efficiently conducting nonlinear time history analyses for a wide range of multi-span bridge configurations.In this tool (Fig.15(a)),bridge structures,abutments,and foundation response mechanisms are integrated within a unified framework.Furthermore,MSBridge allows for addressing possible variability in the bridge deck,bent cap,column,foundation,and/or ground configuration properties (on a bent-by-bent basis).As such,MSBridge permits the simulation of key scenarios of significance for bridge upgrades,widening,extensions,and retrofits.Convenient postprocessing capabilities allow graphical visualization of the results including the deformed mesh (Fig.15(b)),as well as column/pile response.Using MSBridge,it is possible for structural engineers/researchers to rapidly build models of complex multi-span bridges,run the FE analysis,evaluate performance of the bridge-ground system,and assess the PBEE outcomes [Elgamal,Lu and Mackie (2014);Almutairi,Lu,Elgamal et al.(2018)].

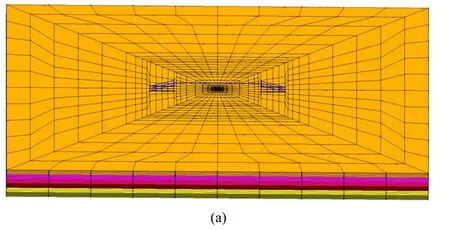
Figure 14:PBEE analysis of a bridge-ground system [Mackie,Lu and Elgamal (2012)]:(a) FE mesh (created in BridgePBEE);(b) Mean repair cost ratios (case 1 represents stiff ground,and Case 2 represents soft ground)

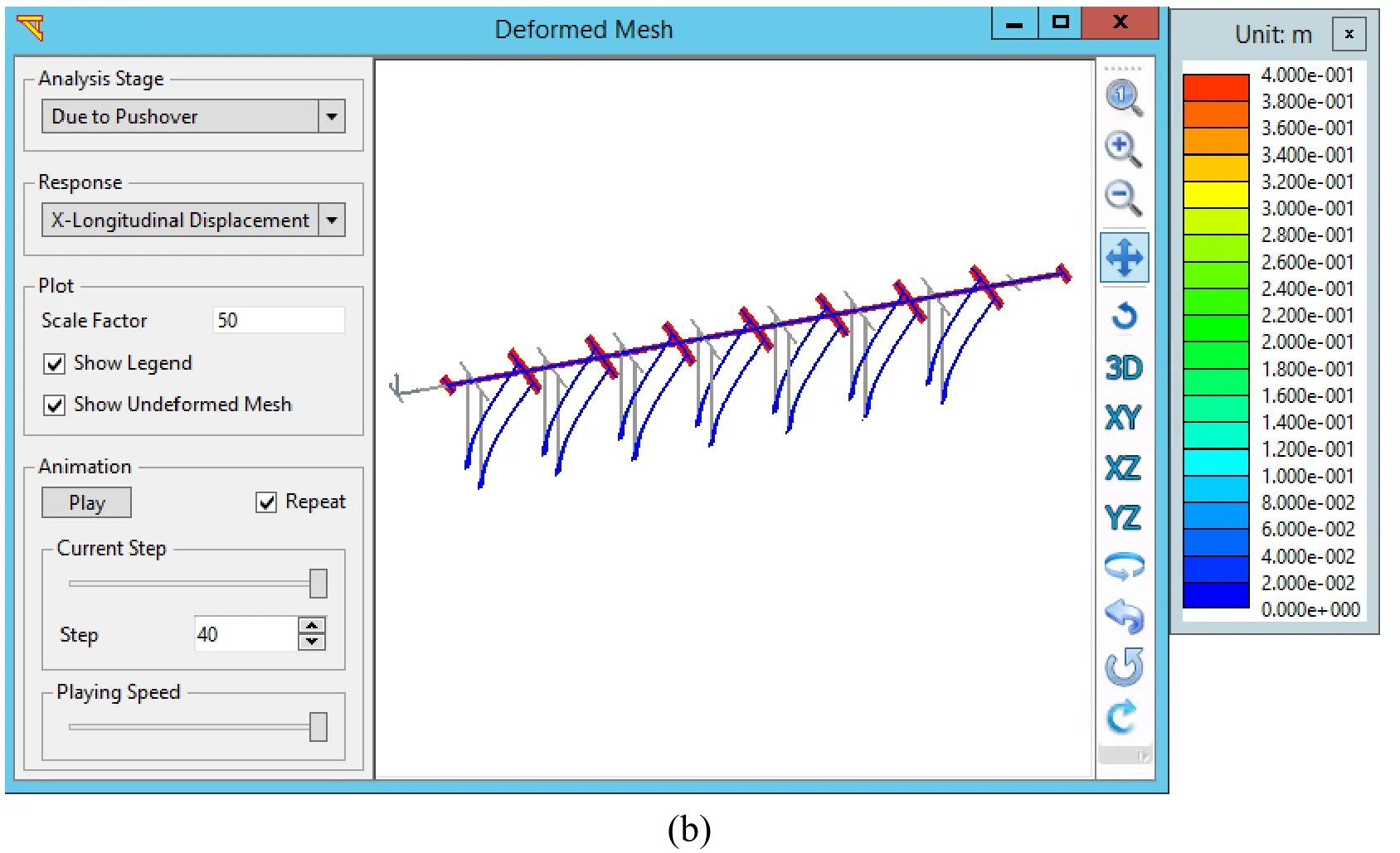
Figure 15:Pre- and postprocessor graphical interface MSBridge [Elgamal,Lu,Almutairi et al.(2017);Almutairi,Lu,Elgamal et al.(2018)]:(a) FE mesh of a multi-span bridge;(b) Deformed mesh of the bridge model under lateral loading (scale factor=50)

In summary,the main capabilities of MSBridge include:i) horizontal and vertical alignments,with different skew angles for bents/ abutments;ii) beam-column element with fiber section for bridge columns and piles;iii) deck hinges,isolation bearings,steel jackets,and abutment models;iv) foundation represented by Foundation Matrix or soil springs (py,t-z and q-z);v) analysis for suites of ground motions (built-in and/or user-defined);vi) PBEE outcomes in terms of repair cost,time and carbon footprint;and vii) pushover and mode shape analysis options.

6 Summary and conclusions

Recent research efforts that address the static and dynamic/seismic response of groundfoundation-structure systems have been presented.Specifically,developments within the computational platform OpenSees were outlined.Representative numerical results were included for the response of large foundation-ground-structure systems,ground modification liquefaction countermeasures,and PBEE analyses.To facilitate 3D computations,graphical user interfaces (OpenSeesPL,BridgePBEE and MSBridge) were shown to be useful tools for conducting simulations of ground modification,ground-pile SSI,and multi-span bridge-ground systems with PBEE assessments.

Overall,the presented studies aim to illustrate the potential for further reliance on computer simulation in the assessment of nonlinear SSI response.Challenges in calibration and in high fidelity modeling are being gradually overcome.With careful attention to the involved modeling details,effective insights may be gleaned for a wide range of practical applications.

Acknowledgments:This research was supported by the Pacific Earthquake Engineering Research (PEER) Center,Caltrans,and the National Science Foundation (Grant CMMI-1201195,OISE-1445712).Additional support was provided by National Science Foundation (NSF) through computing resources provided by San Diego Supercomputer Center (SDSC) and Texas Advanced Computing Center (TACC).The Wharf layout information was provided by Dr.Arul K.Arulmoli,Principal,Earth Mechanics,Inc.