基于模糊贝叶斯风险和T-S模糊模型的故障诊断

路 涛1， 梁智超2， 索明亮34

(1.空军装备部外场保障局，北京 100843； 2.复杂航空系统仿真实验室，北京 100076；3.北京航空航天大学可靠性与系统工程学院，北京 100191； 4.可靠性与环境工程技术重点实验室，北京 100191)

复杂装备的诞生是工业技术快速发展的必然结果，随之而来的是对复杂装备的健康管理问题。模型方法对此已经不再适用，随着智能时代的到来以及装备数据的不间断采集和存储，数据驱动的健康管理技术是维护复杂装备的有效手段之一，业已取得了较为丰硕的成果[1-5]。但是，如何有效挖掘数据背后隐藏的有价值信息，如何降低基于数据驱动故障诊断的风险，是数据驱动故障诊断所面临的重要挑战。

对于数据驱动故障诊断而言，诊断知识的获取是其瓶颈问题，具体包括敏感数据选取、诊断规则的提取。其中，敏感数据选取又包括数据的清洗预处理、属性子集的选择。本文重点围绕属性子集选择和诊断知识获取两方面问题开展研究。

属性选择方法可大致分为3个类别[6]：过滤式方法(Filter)、封装式方法(Wrapper)和嵌入式方法(Embedded)。其中，封装式方法和嵌入式方法更倾向于得到符合学习机的结果，但可能存在过拟合问题。而过滤式方法则具有更好的泛化能力和快速性。对于故障诊断问题而言，选取相对最优的属性子集以提高诊断的准确率是筛选属性选择方法的一个重要标准。

另一方面，基于数据诊断知识的获取包括统计分析、阈值判断、包络分析和模糊规则等方法。对于强耦合复杂化的数据而言，常规方法已不再适应未来发展[1]。有效刻画知识内涵，得到符合自然认知易于解释的诊断规则是故障诊断的发展方向之一。

综合上述分析，本文基于模糊贝叶斯风险模型(Fuzzy Bayes Risk Model,FBR)和T-S模糊模型实现数据的知识获取和诊断决策。其中，贝叶斯风险模型以风险最小化原则提取属性子集，旨在最大程度地降低诊断风险；T-S模糊模型利用分段线性化思想，以线性函数无限逼近复杂非线性的数据知识。最后，以C-MAPSS发动机实验数据为研究对象，验证本文诊断方法的有效性。

1 基于FBR-TS的故障诊断模型

1.1 模糊贝叶斯风险模型

1.1.1 基本理论

定义1：(贝叶斯风险模型)[7]给定一个决策系统DS={U,C∪D,V,I}，U(U={x1,x2,…,xm})为论域，C(C={c1,c2,…,cn})为条件属性，D(D={d1,d2,…,dK})为决策属性，V为值域，I为上述属性之间的映射函数。对于关于条件属性c∈C的任意样本xi∈U，通过某种度量方式可能将其划分到D中的任意决策类别，但是根据信息函数I该样本属于确定的决策类dk∈D，即样本xi的名义决策类为dk。因此，关于c的样本xi归属于dk的贝叶斯风险表示为

(1)

从式(1)可以看出，损失函数和概率影响贝叶斯风险的结果。其中，损失函数考虑了条件属性的分布情况，用于估计样本被错分的损失；概率则源自于条件属性和决策属性之间的关系。因此，贝叶斯函数充分地考虑了数据的分布情况和属性间的耦合关系，可全面地挖掘数据背后隐藏的有价值信息。

常用的损失函数为0-1模型，或借助领域专家或大量统计实验得到损失函数。但上述方法不能有效评估决策中的真实损失，或在实际应用中受到了限制。文献[7]通过分析数据分布特性，给出了一种基于高斯核的损失函数。

定义2：(高斯核损失函数)给定一个决策系统DS={U,C∪D}，c∈C，D={d1,d2,…,dK}，对于U中的任意样本xi，其名义决策类为dk，利用某种度量得到的可能决策类为dj，其中，dj,dk∈D。则xi在c下的高斯核损失函数定义为

(2)

式中，μk是关于c的样本集属于dk的期望；σk为当前数据分布的标准差。

对于定义2，有以下3点解释：

① 如果样本被划分到自己的名义决策类中，即k=j，则其损失为0；

② 如果样本越靠近其分布内的期望，则该样本的错分损失越大；

③ 如果标准差为0，则当前分布内所有样本的损失为1，这意味着当前分布内所有样本均等。

定义3：(模糊邻域)在决策系统DS={U,C∪D}中，给定任意样本xi∈U和条件属性c∈C，xi在条件属性c下的模糊邻域Nc(xi)定义为

Nc(xi)={xj|xj∈U,fc(xi,xj)≥δ}

(3)

式中，δ为邻域阈值；f(·,·)为模糊相似度，即

(4)

式中，m为U中样本个数(m>1)；MD(·,·)为马氏距离，表示为

(5)

式中，“-1”为求逆运算，上标T为转置运算符。

对于式(4)的模糊关系，显然有以下属性成立：

①f(xi,xi)=1；

②f(xi,xj)=f(xj,xi)；

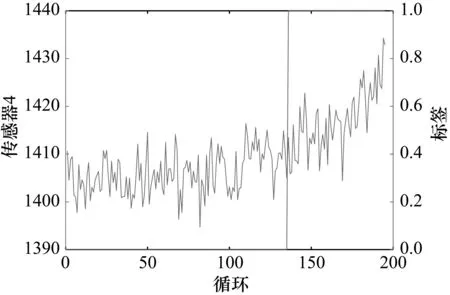
③ 0

定义4：(分类概率)给定一个决策系统DS={U,C∪D}，对于条件属性c∈C下的任意样本xi∈U，其模糊邻域为N(xi)={x1,x2,…,xm}，对应的决策类别集合为N(d)={d1,d2,…,dp}，N(d)⊆D。则样本xi划分到决策类dj∈N(d)的概率为

(6)

式中，dj为样本xi的名义决策类。

对于式(6)，显然有0≤Pc(dj|xi)≤1成立。其中，若Pc(dj|xi)=0成立，则当且仅当以下3个条件同时成立：① 邻域阈值δ=0；②f(xi,xk)=0；③ 在模糊邻域N(xi)中有且只有xk属于dj。另一方面，如果样本xi的名义决策类为dj，则Pc(dj|xi)≠0。

上述贝叶斯风险模型中考虑了样本之间的模糊关系，基于模糊相似性得到了样本的分类概率。因此，该贝叶斯风险模型可称为模糊贝叶斯风险模型。

定义5：(模糊贝叶斯总风险)给定决策系统DS={U,C∪D}，属性子集B(B⊆C)关于决策属性D的总风险表示为：

(7)

1.1.2 属性子集选择与赋权

定理1：给定决策系统DS={U,C∪D}，B1⊆B2⊆C，给定邻域阈值δ，则有：

①fB1(xi,xj)≥fB2(xi,xj)；

③RB1≥RB2。

该定理相关证明可参见文献[8]和文献[9]。该定理体现了FBR模型的单调性，因此可依据该定理设计启发式前向贪心属性子集选择算法，筛选出一个具有相对最小决策风险的属性子集。所设计的属性子集选择算法如图1所示。

图1 基于FBR的前向贪心属性子集选择算法

1.2 T-S模糊模型

定义6：(T-S模糊模型)给定决策系统DS={U,C∪D}，C={c1,c2,…,cn}，D={d1,d2,…,dK}。给定测试样本X={x1,x2,…,xn}，对于其中任意条件属性ci∈C下的测试样本xi∈X，其中T-S模糊规则Rci可表示为：

Rci:IFxiinA,THEN

Yci(D|xi)={yci(d1|xi),yci(d2|xi),…,yci(dK|xi)}T

={a1xi+b1,a2xi+b2,…,aKxi+bK}T

式中，A为论域U下的某个区间；ak,bk为后件规则参数，k=1,2,…,K。

由此可得测试样本X基于此T-S模糊模型的输出矩阵为

Y(X)=(Yc1(D|x1),Yc2(D|x2),…,Ycn(D|xn))

(8)

(9)

上述T-S模糊模型与传统的T-S模糊模型区别在于，将样本分配至每个条件属性，然后计算其对应于每个决策类别的模糊函数，从而得到相应的模糊输出矩阵。

该模糊模型与传统T-S模糊模型一样，具有两个难点：① 规则个数的确定问题；② 后件规则参数的确定问题。针对不同的研究对象，规则数往往是不同的。通常情况下，依靠专家经验获取规则个数。而后件规则参数的确定则依赖于线性分段个数(即规则个数)和拟合手法，常用的拟合方法为最小二乘法。在拟合手法一定的情况下，规则个数的变化将直接影响T-S模糊模型输出结果的可靠性。另一方面，在获取拟合依据时所采用的拟合基准也是建立T-S模糊模型的一个重要因素。本文提出的模糊贝叶斯风险模型利用高斯核模糊邻域关系衡量样本隶属于决策类的可能性，反映了样本相对于决策类别的隶属关系。因此，本文以FBR中的模糊分类概率为拟合基准。

定义7：(模糊分类概率矩阵)给定决策系统DS={U,C∪D}，根据式(6)可得任意样本xi∈U基于条件属性B⊆C在决策类别dk∈D的分类概率为PB(dk|xi)，则该论域基于B在决策属性D下的模糊分类概率矩阵定义为

(10)

1.3 诊断模型建立

根据上述理论可设计基于模糊贝叶斯风险和T-S模糊的诊断模型如图2所示。

图2 基于FBR和T-S模糊的故障诊断模型

图2中的初始数据集DS又可称为训练数据集，用于训练该诊断模型生成知识库，测试数据X中的样本个数等于属性子集中属性个数，且与选择的属性一一对应。在训练生成知识库的过程中，3个步骤是递阶进行的，首先利用FBR从训练数据集DS中选取属性子集以节省存储空间并提高计算效率，然后利用属性子集选择过程生成的条件属性风险值确定属性权重，并将此期间得到的模糊分类概率分配给T-S模糊模型完成模糊规则提取。在训练过程得到的属性子集、属性权重、模糊规则前件和后件组成知识库，用于诊断。在给定测试数据后，依据生成的知识库得到的决策结果是概率形式的，即得到测试数据被划分到各个决策类别的概率大小。根据概率形式的决策结果即可排序得到最终决策。

2 数值实验与结果分析

2.1 实验设置

以NASA发布的商用模块化航空推进系统仿真(C-MAPSS)实验数据[10]为研究对象，验证所提诊断模型的有效性。C-MAPSS数据集共包含4个子集，分别为FD001，FD002，FD003和FD004，包括多台相同型号发动机在不同工况和故障模式下的利用21个传感器采集的数据。为保证实验数据的可用性，本文选取单工况下的数据集为研究对象，即FD001和FD003。由于每组数据集内的发动机型号相近，所选取的发动机型号对实验验证没有影响。所以，分别选取FD001中编号21(FD001-21)和FD003中编号16(FD003-16)的发动机数据。以FD001-21中3#和7#传感数据为例，得到其拟合分布情况如图3、图4所示。可以看出，在模糊贝叶斯风险模型中应用的高斯核函数适用于C-MAPSS数据。

数据标签是标定数据类别的标准，根据文献[11]的建议，利用线性分段函数方法获取数据标签。图5、图6所示为以FD001-21中4#传感器训练数据和FD003-16中14#传感器训练数据为例，说明标签的生成结果。其中，标签中“0”代表正常状态，“1”代表异常状态。

图3 FD001-21传感3数据分布情况

图4 FD001-21传感7数据分布情况

图5 FD001-21中4#传感器训练数据

图6 FD003-16中14#传感器训练数据

为验证所提诊断模型的有效性，选取一些常用和最新的属性选择方法与FBR模型做对比。包括ReliefF[12]、mRMR(Min-Redundancy Max-Relevance)[13]、FDAF(Fisher Discriminate Analysis F-score)[14]、DRJMIM(Dynamic Relevance and Joint Mutual Information Maximization)[15]和NRS(Neighborhood Rough Set)[16]。其中，ReliefF和mRMR为成熟且常用的属性子集选择方法，FDAF和DRJMIM为最新的属性选择方法，NRS为经典的基于粗糙集的启发式选择方法。值得注意的是，除NRS和FDAF外，其他方法需要预先指定所需选择的属性个数，而FDAF在属性选择时借助了支持向量机迭代搜索最优的属性集合。所以，为了更有效、公平地对比验证，按照文献[17]给出的建议，其他方法所选择的属性个数等于NRS方法所得到的个数。DRJMIM在处理数据前需要对原始数据进行离散化，因此为保证离散化对DRJMIM方法的影响最小，本文选取表现相对优异的SMDNS(Supervised and Multivariate Discretization Algorithm)离散化方法[18]协助DRJMIM完成属性赋权，其参数根据文献[18]的建议选取为0.8。按照文献[16]的建议，NRS的邻域半径选择为0.2，本文FBR的邻域阈值为0.7。为保证对比的可靠性，在应用各个模型进行诊断时，所有权重均依据FBR得到。

为验证结果准确度，依据如下的诊断准确率公式：

(11)

式中，Nr为正确结果，Nall为所有的诊断结果。

2.2 诊断过程及结果分析

以FD001-21中训练数据为例，演示本文所提方法的计算过程。

在FD001-21训练数据中，包含21个条件属性(传感器数据采集点)和195组样本集。在属性子集选择过程中，首先将属性子集置空，然后依次加入候选的条件属性，根据模糊贝叶斯风险理论可计算各个条件属性的风险为83.0769，57.2818，56.9003，51.8188，83.0769，82.1658，52.6400，64.3436，44.2004，83.0769，49.5547，50.1624，66.6539，44.0804，57.2911，83.0769，56.9316，83.0769，83.0769，57.4249，54.5914。通过上述风险结果可以看出，风险最小的条件属性为14，风险值为44.0804。因此，属性14将被第一个放入属性选择的子集中。然后，依次将剩余条件属性和当前的属性子集(由已选择的条件属性14构成)结合，重新计算组合属性集的风险值。如此遍历执行，直至风险值不再降低，则输出所有已选择的条件属性。对于FD001-21的训练数据，得到的属性子集由条件属性14、3、7、17、11、9、13、4、2、12、8组成。则对应的属性权重可计算为0.0973，0.0891，0.0918，0.0891，0.0938，0.0973，0.0828，0.0923，0.0888，0.0934，0.0843。

在计算模糊贝叶斯风险时，生成的模糊概率则组成属性子集的概率矩阵，然后根据样本的区间划分，生成T-S模糊规则前件和后件。由于条件属性个数较多，且规则个数较多，不便给出数值结果。以FD001-21中4#传感器训练数据和FD003-16中14#传感器训练数据为基础，利用模糊贝叶斯和T-S模糊模型得到二者的模糊规则分段函数可表示为如图7、图8所示结果。其中，规则个数为15。

对比图7、图8中数据实际分布情况，可以看出，对于正常和异常状态区分明显的数据区间，会得到区分明显的隶属度函数。相反，两种状态区分不明显的数据区间会存在隶属度状态交叠区域。这符合人们的一般认知，证明所提取的模糊规则是合理的。

图7 FD001-21中4#传感器训练数据生成的T-S模糊规则

图8 FD003-16中14#传感器训练数据生成的T-S模糊规则

对于FD001-21和FD003-16发动机训练数据，各个方法得到的属性子集及依据属性子集和本文T-S模糊模型得到的诊断结果如表1、表2所示。

表1 FD001-21属性子集选择结果及诊断准确率

表2 FD003-16属性子集选择结果及诊断准确率

表1、表2所示结果表明，本文所提的诊断模型得到的诊断准确率最高，其次为NRS模型，而ReliefF、FDAF和DRJMIM相对较差。因为FBR模型是基于贝叶斯风险最小化原则利用启发式贪心搜索思路寻找相对最优特征子集，并充分考虑了数据之间的模糊关系，因此得到了较为准确的诊断决策结果。NRS基于粗糙空间划分思想，以邻域为基本粒子，利用属性和数据的依赖度实现属性子集选择，也是较为充分地考虑了空间数据的特征关系。ReliefF为原始的Filter型属性选择方法，属性选择思想简单明了，但无法深层次挖掘数据特性。mRMR和DRJMIM均为基于信息论的属性选择方法，但DRJMIM很大程度上依赖于数据离散化方法，使得其不能得到理想的决策结果。FDAF是F-score的改进版本，其属性选择本质上还需要依赖于分类算法的复杂，没有分类算法的帮助，导致其不能选取相对最优的属性子集。另外，与依据原始数据得到的诊断结果对比可以看出，合理地筛选用于诊断的传感器数据，可降低数据冗余度，提高诊断准确率。

3 结论

针对数据驱动故障诊断中知识获取和诊断决策问题，提出了一种基于模糊贝叶斯风险和T-S模糊模型的故障诊断方法。利用模糊贝叶斯风险模型提取相对最优属性子集，并利用其生成的概率分布得到T-S模糊规则，实现数据驱动的故障诊断。通过C-MAPSS发动机故障诊断问题，与不同属性子集选择方法进行了对比研究。实验结果表明，本文所提诊断方法得到的结果准确率最高，诊断准确率均超过了0.95，适用于复杂装备的数据驱动故障诊断。

值得注意的是，知识获取的速度是数据挖掘研究的另一个重点方向，本文未对此进行研究和分析。在未来的研究工作中，可基于本文所提诊断方法，提高其数据挖掘的速度。另一方面，本文所提方法有两个参数需要人工设置，即FBR中的邻域半径和T-S模糊规则个数。其中，邻域半径决定了空间粒子划分的精细程度，模糊规则个数则决定了对复杂系统知识的拟合程度。实际上，可以借助分类器和优化算法从训练数据中得到较优的参数组合，以提高模型的自动化实践水平。