基于PCA优化的神经网络飞机燃油消耗预测方法

(空军工程大学 航空工程学院，陕西 西安 710038)

飞机是一种燃油消耗巨大的航空器。对于民用飞机而言，航空燃油消耗直接关系到航空公司的运营效益[1]；对于军用飞机而言，燃油消耗对地面保障和任务规划影响极大。对飞机的燃油消耗进行合理预测，并以此为基础对燃油进行管理、规划飞行任务等对于提升航空运输的经济性与飞机的任务能力都具有重要意义。

飞机燃油的消耗受到诸多因素的影响，而且多个影响因素之间存在极强的非线性耦合效应，导致利用传统方法对飞机燃油消耗建模存在较大困难。文献[2]和文献[3]分别利用多元线性回归模型和基于随机森林算法建立的回归模型对飞机燃油消耗进行了预测，模型较为简单，但忽略了飞发交互效应和非线性因果关系；文献[4]和文献[5]建立了基于能量守恒原理的燃油消耗模型，主要缺点是模型性能参数难以获得，且没有考虑气象条件以及飞机“油耗油”问题对油耗的影响[6]；文献[7]提出了基于轨迹模式识别的计算方法，主要用于估算，不宜精确预测；文献[8]利用飞行动力学方程建立了飞机燃油消耗动力学模型，预测精度还有待提高。Chang等人建立了基于飞行数据模糊逻辑模型的运输机燃油消耗模型[9]，预测的精度较高，但模型较为复杂；Park等人利用飞行轨迹数据和总能量模型飞燃油消耗进行了估算[10]，解决了工程实际应用困难的问题，但在精度上有所欠缺；Vazquez等人利用动力学数值分析建立了飞机的油耗模型[11]，具备可操作性强的优点，但是其诸多理想化假设条件忽略了发动机工况等对燃油消耗的影响因素。Khadilkar[12]等利用飞参数据建立了燃油消耗多变量函数模型，变量数据在工程实际中难以获得；飞参数据是记录的飞机、发动机以及其他设备的状态数据，是建立飞机燃油消耗的重要依据[13]。Elman神经网络适用于预测时间序列，对于受历史飞行状态影响较大的耗油速率适应性较好。鉴于以上分析，本文选取了Elman神经网络，经过主成分分析法降低输入维数，利用Elman神经网络对飞机燃油消耗进行了预测，并将该网络与其他网络及未经PCA法处理的Elman网络进行了对比，最后利用K-S检验法验证了其预测误差服从正态分布，并依据验证结果对预测值进行了进一步修正。

1 主成分分析基本原理

主成分分析法(Principal Component Analysis，PCA)是一种降维处理方法，通过线性变换转变为其他几个不相关的指标，新指标按照方差递减顺序依次排列[14]。

1.1 归一化处理

设有n个相互关联的m维变量作为输入，记为X1,X2,…,Xn，样本采集数为j,则样本矩阵Xm×n为

(1)

其中,

(2)

(3)

(4)

令

(5)

即完成原始样本矩阵的归一化处理。

1.2 计算各变量之间的相关矩阵R

(6)

其中,

(7)

l=1,2,…,m;p=1,2,…,m;q=1,2,…,n。

1.3 计算主成分

利用Jacobian法求解相关矩阵R的所有特征值λk(k=1，2，…,n)及其对应的特征向量并将特征根由大到小排列，分别计算出对应的主成分。主成分计算需要确定主成分的个数，一般由方差贡献率和累计贡献率确定。

主成分Zk的方差贡献率Pk为

(8)

式中,λk为主成分Zk在全部方差中所占的比重。前c个主成分的累计贡献率Pc为

(9)

2 实例建模分析

2.1 飞机燃油消耗因素的主成分分析

输入的飞参数据数据项经过筛选后一共有21项。现对经过归一化处理后的数据进行主成分分析，经过主成分变换后，原先的21个变量经过线性变换为21个主成分，按照大于80%的累计贡献率进行筛选，最终只留下前5个主成分作为神经网络输入。现给出前5个主成分按照特征值、方差贡献率以及累计贡献率，如表1所示。

表1 主成分的特征值、方差贡献率与累计贡献率

成分矩阵反映了主成分包含的原有变量信息的丰富程度。数值越大，则表明该主成分包含的某原始变量的信息越多。主成分与原始变量的关系可以得到这5个主成分的反映原始数据信息的能力，如表2所示。第1主成分主要包含了发动机因素(发动机的各项状态参数，纵向加速度很大程度上取决于发动机推力)、大气因素(飞行高度)、速度因素(马赫数)、重量因素(总剩油量)；第2主成分主要包含了爬升因素(俯仰角、升降速度)；第3主成分主要包含了速度因素(飞行速度、马赫数，发动机进口气流总温取决于来流速度)；第4主成分主要包含了升力因素(法向加速度、迎角)；第5主成分主要包含了机动因素(横滚角，侧向加速度)。

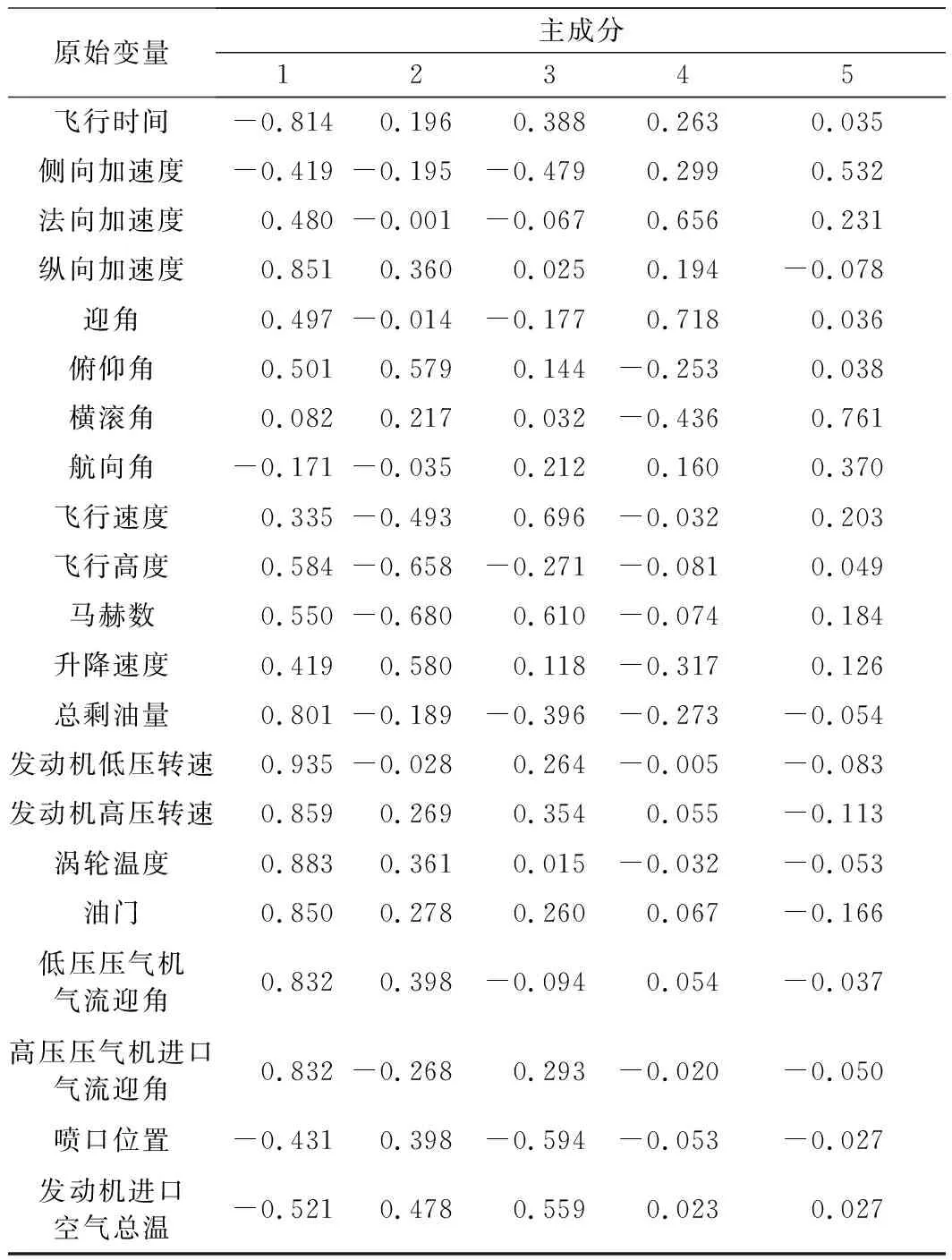
表2 成分矩阵所含信息

可见这5个主成分能够充分反映21个原始变量的有效信息，对所有的影响因素进行了解耦和线性组合，并与实际影响飞机燃油消耗的因素相符合，在充分保留原有信息的同时进行了降维处理。

2.2 飞机燃油消耗的神经网络预测

2.2.1 训练数据和测试数据的选取

为了充分证明Elman神经网络对飞机燃油消耗预测的准确性，本文对某型同架飞机不同飞行剖面的两个架次飞参数据进行了采集，并将一个73 min的飞行架次采集的飞参数据作为训练数据，将另一个47 min的飞行架次的数据作为测试数据进行预测，两个架次分别称为架次1和架次2，采集时间间隔设定为1 min，以避免样本数过多产生过拟合。

2.2.2 神经网络结构设计

经过试验，网络一共包含30个神经元，其中隐含层包含10个神经元，输入和输出层均包含10个神经元。训练函数为traingdx函数，输入层到隐含层的传递函数为transig函数，隐含层到输出层的函数为purelin函数。

2.2.3 训练和测试

经过10000次迭代后，网络的均方误差(MSE)已经降低到10-3以下，符合飞机燃油消耗预测的需求。利用训练完毕的网络进行预测，平均相对误差为4.29%，均方相对误差为0.34%，符合工程上的误差要求。为训练和预测的结果对比，如图1所示，利用架次1数据训练得到的网络仍然能对架次2有良好的预测效果，说明主成分分析与Elman神经网络结合的方法能够充分挖掘飞参内部的有效信息，具备良好的非线性映射能力。

图1 Elman神经网络训练和预测结果

现利用在主成分分析基础上的BP、GRNN和RBF 三种神经网络,未经过主成分分析法处理的Elman神经网络的预测结果以及经过主成分分析法处理的Elman神经网络进行对比。5种预测方法的预测结果与飞参系统记录数据的对比如图2所示。可以看出，BP网络的预测趋势虽然基本符合油耗规律，但是部分区间预测结果波动过大，且出现大量尖峰值；GRNN网络只能大体给出油耗趋势，预测值则与实测值之间的差值过大；RBF网络则出现病态数据。

未经主成分分析法降维处理的网络的预测效果不如经过主成分分析法优化的Elman网络，但是却仍然远优于其他三种网络;经主成分分析法处理后的Elman神经网络拟合效果更接近真实值，3项误差指标分别只有未经处理的6.45%、29.96%、22.24%，在网络的训练时间上提升了6 s,如图3与表3所示。由此可以得出结论，Elman神经网络的经过主成分分析降维处理后的网络在误差性能和收敛性上均有较大提升。

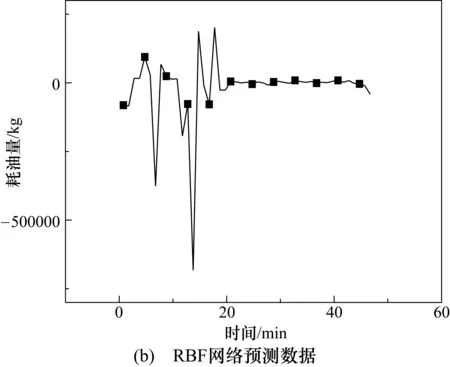
图2 不同网络预测效果对比

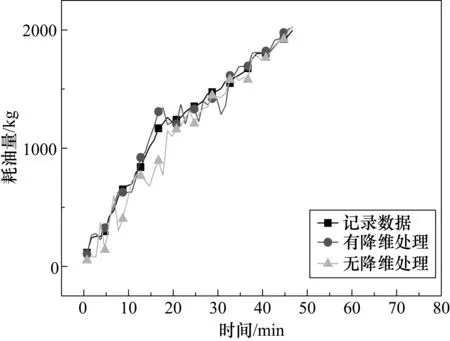
图3 有无主成分降维处理预测效果对比

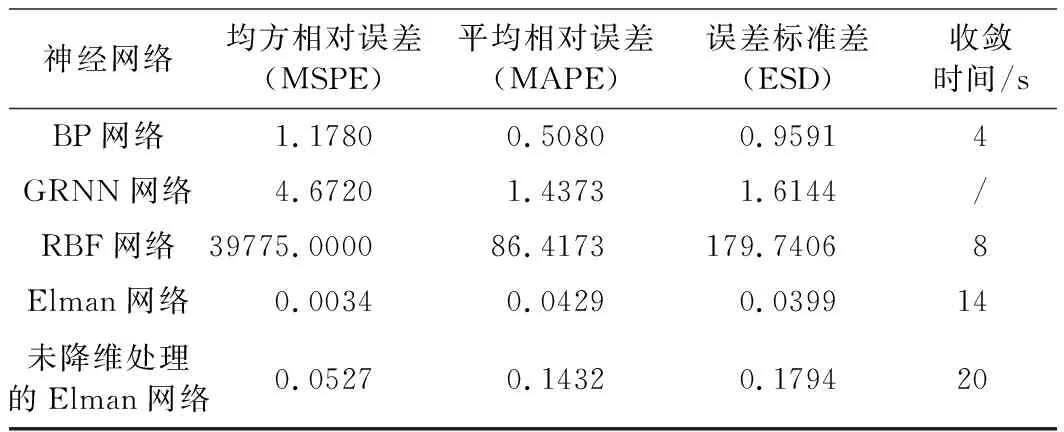
神经网络均方相对误差(MSPE)平均相对误差(MAPE)误差标准差(ESD)收敛时间/sBP网络1.17800.50800.95914GRNN网络4.67201.43731.6144/RBF网络39775.000086.4173179.74068Elman网络0.00340.04290.039914未降维处理的Elman网络0.05270.14320.179420

3 基于K-S检验法的预测结果冗余修正

在工程实际问题中，往往需要设计有一定的冗余度或设置安全系数。为满足飞行安全要求，现对误差分布进行研究并求得安全系数β，修正预测结果。现提出一种基于Kolmogorov-Smirnov检验法(以下简称“K-S检验法”)的预测结果冗余修正方法。令实际值为U=[U1,U2,…,Ut]T,预测值为V=[V1,V2,…,Vt]T，实际值与与预测值之间的相对误差为δ=[δ1,δ2,…,δt]T(此例中t=47)，显著性水平α=0.05，对误差进行K-S检验是否服从正态分布。K-S检验的渐进显著性为0.827，大于显著性水平α，接受原假设，并服从N(-0.003,0.0049)分布，结果如表4所示。

表4 误差分布的K-S检验结果

取燃油预测值置信度为95%的置信区间[a,b]=[-0.0232,0.0170]，取置信区间下限的相反数为预测结果安全系数β=-a=0.0232,则经修正后的预测值为VM=(1+β)V,即经过修正后的燃油消耗的预测值是原始预测值的102.3%，保证飞机预测油耗在95%的可能性下高于实际油耗。

4 结束语

(1) 利用主成分分析法将21个飞参参数简化为5个主成分，分析了成分矩阵，降低了神经网络的输入维数，提高了Elman神经网络的性能。将主成分分析得到的数据作为输入，对某架次的飞机燃油消耗进行了预测，结果表明预测值与实测数据偏差较小。

(2) 将Elman神经网络的预测结果与其他几种网络以及未经主成分分析法改进的神经网络进行了对比试验，验证了前期网络筛选的结果，也证明了主成分分析法对神经网络性能具备改进作用。

(3) K-S检验法证明Elman网络的预测误差服从正态分布，以此为基础，为保证飞行安全冗余，利用95%置信区间下限得到安全系数β,进而得到修正后的预测值。

(4) 针对飞行燃油消耗的神经网络的结构优化可以做进一步研究，以提高预测性能。