小波特征提取和随机森林模型解析色谱重叠峰

(东南大学 仪器科学与工程学院，江苏 南京 210096)

在复杂物质的色谱法解析过程中，经常会有色谱峰重叠[1]的情况发生。目前，用于重叠峰分解的方法有以下几种：传统的傅里叶变换和导数等方法对噪声敏感，降低了信噪比而不利于定性定量分析；垂线法和切线法的原理简单、计算速度较快，但是对一些重叠峰分解的精度可能会出现较大误差；曲线拟合法[2]实现过程和运算都比较复杂，难以实现色谱曲线实时处理，在实际的应用中有一定的局限性；小波变换方法虽然运用广泛[3-4]，但容易引起变换后曲线重构的信号不准确；神经网络法利用了其较强的非线性映射能力计算子峰面积比，但其数学模型较为复杂，网络结构选择不一，只能凭借经验选取，并且它的计算量大，网络的收敛速度也较慢。

随机森林模型是一种基于决策树的算法，被归类为机器学习中的一种方法[5]。它具有模型简单、训练速度快、预测精度高、泛化能力强等突出优点。本文结合了神经网络法的思想，对随机森林模型在色谱重叠峰分解领域的应用进行了研究。首先利用gaus1小波分解系数来模拟导数，利用小波分解计算过程中自动消除噪声的特点，直接从原始的信号中提取相应的导数特征点；然后并以特征点作为模型输入、重叠峰子峰面积比作为模型输出，使用交叉验证的方式确定模型参数，对随机森林模型进行有监督的训练；最后使用训练好的模型拟合待测色谱重叠峰信号的各子峰面积比，实现重叠峰的解析。

1 重叠峰解析基本原理

色谱峰信号一般使用高斯函数来拟合，表达式为：

(1)

式中,t为信号采样时间;h(t)为信号在时间t时的强度;H为色谱峰信号的最大值;T为峰的保留时间;σ为峰拐点距离峰保留时间的距离。如果色谱峰不对称，则：tT时，σ=σb。因此σa+σb、σa/σb分别代表了一个色谱峰的宽度和它的不对称度。

对于一个由两个色谱峰叠加而形成的重叠峰，即可以用H1、T1、σ1a、σ1b、H2、T2、σ2a、σ2b八个参数来唯一决定。并且对于化学色谱峰，可以假设两个子峰的不对称度相同，即有σ1a/σ1b=σ2a/σ2b，这样参数的数量就减少到5个。此时可定义此重叠峰的子峰面积比Q如下，其中S1、S2分别为两子峰面积。

Q=S1/S2

(2)

(3)

色谱重叠峰的分离度RS定义为

(4)

式中，Wi为峰1、峰2的峰底宽度。RS的值越小，则两峰重叠的越厉害。当RS较小时，两峰已不能用肉眼识别；当RS接近1.5时,两峰已基本分离。本文研究的重叠峰分离度RS范围为0.5～1.4。

色谱重叠峰信号的特征点有起点、拐点、谷点、顶点、终点等，它们是色谱信号中的突变点或是奇偶点，包含了较为重要的信息。由于重叠峰具有前肩峰、后肩峰等不同的形状，所含有的特征点种类和数量都不相同。只有拐点是所有形式重叠峰都具有的特征点，这些点的横纵坐标与子峰面积比之间一定存在着某种联系，但无法用简单的函数关系式表示出来。考虑到随机森林模型具有对任意函数进行拟合的能力，并且具有训练速度快，拟合精度高等优点，因此本文选取其对上述关系进行拟合。

2 连续小波变换计算色谱曲线拐点

导数在信号处理领域发挥着着十分重要的作用，但在实际的色谱分析过程中，信号往往含有较大的噪声。如果使用点到点微分的方法，求导结果曲线中往往也含有大量噪声。此时使用二阶导数法求取色谱重叠峰拐点，就可能因为噪声而难以计算出准确的结果。

小波变换为色谱信号求导提供了新的思路，小波变化的小波分解系数可以用来模拟求导[6]。根据小波分解的性质，如果选取的小波满足小波容许条件，在进行变换的过程中能够自动地对噪声进行消除，提高信噪比，得到的结果可以用来模拟导数，弥补了导数法的不足，适用于对色谱重叠峰信号的拐点提取。

本文使用小波模拟一阶导数的极值点来检测原色谱曲线拐点，而不是模拟二阶导数的过零点。有以下几点原因：① 若使用尺度较小的小波在对低信噪比的色谱信号进行分析，小波计算的模拟导数由于仍然存在噪声，可能会在零点附近波动；② 选取较大的分解尺度时，色谱峰会变得锐化，从而有利于极值点的提取。由于高斯函数的各阶导数正好可以满足小波容许条件，本文选取了gaus1函数作为母小波对原色谱信号进行连续小波变换来模拟一阶导数。gaus1函数表达式如下所示,其中C为调整因子。

gaus1(x)=C·e-x2

(5)

图1为模拟的色谱重叠峰并使用gaus1小波分别在3，10，15，25尺度下进行分解得到的细节系数。从图中可以看出，随着分解尺度的增加，小波细节系数也逐渐增大，并且存在4个极值点A、B、C、D。上述小波模拟导数可以代替实际导数计算的理论基础是特征点位置在小波变换前后没有发生变换。实际上在选取不同的分解尺度时，可能会造成特征点不同程度的偏移。下面以某后肩峰为例使用gaus1小波，选取不同尺度进行分解并对其拐点进行计算，得到的结果如表1所示，其中模拟信号的范围为-2000～3000，单位为毫秒(ms)，拐点位置为模拟信号的横坐标值，相对误差定义为位置误差与子峰宽度之间的比值。

表1 不同分解尺度下拐点位置计算结果

可以看出，使用gaus1小波进行变换之后的模拟导数的4个极值点，相较于原色谱信号的拐点，位置误差较小。因此，小波变换的方法具有可行性。

下面在重叠峰信号中加入一定量级的白噪声，对小波模拟导数检测拐点的抗噪性进行分析。图2分别是在色谱信号中加入信噪比为20 dB的噪声后，进行小波变换模拟的一阶导数曲线，以及先进行滑动窗口滤波，然后使用数值微分方法求取的一阶导数曲线。可以看出，虽然原色谱信号被噪声污染严重，但经过小波计算模拟的一阶导数比较光滑，峰形清晰，分辨率较高，明显优于数值微分方法求取的结果。

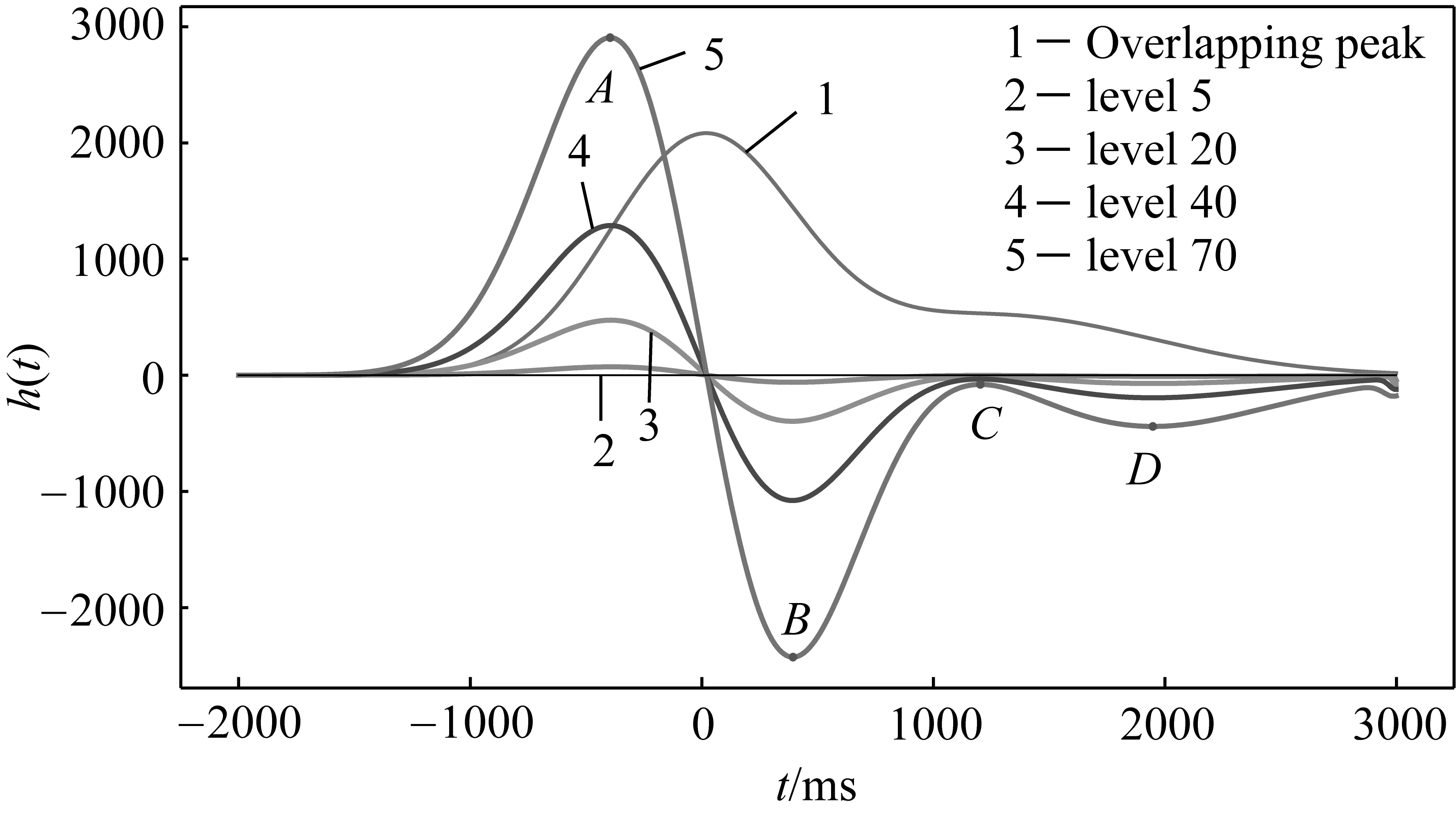
图1 不同尺度的分解结果

图2 一阶导数曲线

可以看出，随着分解尺度的增大，模拟的导数曲线越来越光滑，有利于求取其极值点。但由于尺度的增大，其极值点位置也会发生偏移，因此需要合理选择小波分解尺度。信噪比不同，分解的尺度也应不相同，最优分解尺度应通过观察小波模拟导数的曲线来确定，当模拟导数的谱峰分辨率有了很大提高，并且导数曲线较为光滑时，即认为是合适的尺度。选取了合适的尺度之后，模拟一阶导数曲线也可能存在噪声的残留，但相较于原信号已有非常大的改善，优于使用数值微分方法得到的结果。

3 重叠峰解析的随机森林模型

(6)

为了克服单一决策树模型容易出现过拟合、预测精度不高的缺点，随机森林模型引入了套袋(bagging)[9]和随机子空间的思想[10]。可以证明，这两种方法的运用，不仅可以保证每棵子树节点之间的特征子集都不同，还可以使得随机森林模型中的各回归子树建立更加随机化，保证了相互之间的独立性，从而有效地解决了过拟合的问题，提高了回归分析结果的精度。子树的数量和选取的自变量个数会影响到随机模型的性能，因此本文将使用交叉验证的方式为模型选取合适的参数。除此之外，在构建回归决策树的时候，使用的是CART算法，由于各子树的构建是相互独立的，因此可使用多线程的方式并行实现随机森林模型。

基于随机森林模型进行重叠峰解析的整体思想如图3所示。先按照一定的方式模拟不同情况下的色谱重叠峰，使用上文所述小波变换的方法检测其拐点，为了加快模型收敛，本文由原始的拐点数据生成了5个无因次比值，生成训练和测试使用的数据集；然后基于网格搜索的方式不断调整参数的最优组合，使用10折交叉验证的方式选择最优的随机森林模型参数；最后利用最优参数和CART算法构建并训练模型，使用测试数据集验证模型的结果。

图3 模型训练流程

4 模型的配置和训练

本文参考了神经网络法分解重叠峰中的数据集产生方法和无因次比值计算方法[11]，生成了5400组重叠峰，并按照5:1的比例随机划分成训练集和测试集。然后对训练集和测试集的每一个重叠峰，使用guas1小波进行小波变换模拟其导数，按图4所示求其4个拐点A、B、C、D。参考神经网络方法计算5个无因次比值作为输入，Q1为需要拟合的因变量，使用第3节的方法训练随机森林模型，即可得到自变量和因变量之间的映射关系。

5 实验验证

经过模型的网格搜索和交叉验证，可得到这两个特征在不同取值时的系数曲线。综合考虑性能和模型复杂度，得到最优的参数组合为：特征数量3，回归子树数量为150。

得到最优参数组合之后，本文使用最优参数建立随机森林模型，并使用训练数据集对模型进行训练。最后使用测试集验证模型的精准度。采用均方根误差(RMSE)、最大绝对误差(MAE)、R2决定系数等参数作为评价的依据，定义如下：

(7)

(8)

(9)

表2 模型性能分析

可以看出，随机森林模型对输入输出的拟合能力很强，平均误差不到1%，R2决定性系数达到99%以上，说明了本模型具有较强的学习能力和泛化能力。图4为模型在训练时的学习曲线，训练集和测试集收敛于同一条线，说明没有过拟合的发生。

图4 模型学习曲线

本文还在相同的环境下实验测试了神经网络法和垂线法进行了结果对比。其中，神经网络方法采用的是含有10个隐节点的BP神经网络，激活函数选用单极性sigmoid函数，学习率为0.01，分别设置了不同的迭代次数进行多次训练，结果如表3所示。同时，模拟了不同参数(分离度RS、峰1面积比例Q1)下使用垂线法进行计算，其结果如表4所示。

表3 神经网络性能分析

表4 垂线法结果(—代表出现肩峰)

测试的结果表明，虽然神经网络法也能对输入输出进行拟合，但准确度不如本文的随机森林模型。并且随着网络规模的扩大，若要达到相同误差程度，需要进行成倍规模的计算，训练时间也远远超出。虽然神经网络也可以通过模型调优等方式使结果精度不断提高，但不论是其参数选择还是模型训练的过程，相较于随机森林模型而言都较为繁琐，并且容易陷入过拟合或是局部最优的结果。而垂线法虽然原理简单，计算速度很快，但是其精度会受到重叠峰的分离度和峰形的影响。一般重叠度越高，垂线法计算的误差会越大。并且垂线法无法对肩峰进行分割计算，存在使用的局限性。综合比较各方面而言，本文的模型有着更易理解、参数调节简单、模型收敛速度快、准确率也较高等优点，具有一定的优势。

最后，本文使用型号为NP7000C高压色谱泵和NC3000C系列可见光检测器，在实际中对本模型的结果进行验证。设置色谱泵流速为2 ml/min，梯度程序时间为30 min，检测器波长设为254 nm，流动相为85%的甲醇水溶剂。通过对某一试剂连续进样，控制其前后两次进样的体积比例，人为造成不同比例的重叠峰。对采集到的重叠峰信号进行连续小波变换检测其拐点，并计算无因次比值作为本模型的输入，多次实验的结果如表5所示。

表5 模型实际使用效果

以上实验结果表明本文提出的利用小波特征提取和随机森林模型的重叠峰解析方法可以有效地对重叠峰中的子峰面积比值进行计算，结果优于传统的垂线法和神经网络法。随机森林模型的两大随机特性可以有效地解决神经网络模型中的过拟合问题，提高了回归结果的精度。并且因为模型中各子树之间的相互独立性，可通过多线程构建的方式提升模型的训练速度，从而在性能上具有一定的优势，克服了传统神经网络法计算量大、学习效率低、网络结构参数难以确定的缺点。从而提高了色谱分析效率，保证了分析结果的准确性。

6 结论

随机森林作为一种高效的机器学习模型，已经在很多领域得到广泛的运用，本文将其引入到色谱分析领域。采用本文所述的方法，利用小波变换和随机森林模型分解色谱重叠峰，在精度上优于传统的垂线法和神经网络法。相较于神经网络方法，它模型简单、收敛更快、训练时间更短，因此拥有更高的效率。通过仿真信号和实际色谱信号的实验验证表明，本方法得到的结果较为精准，确保了色谱分析结果的准确性。