基于RBF神经网络-滑模观测器的PMSM无传感器矢量控制

(上海理工大学 光电信息与计算机工程学院,上海 200093)

永磁同步电机具有高功率密度和高效率的特点，因此被作为伺服电机广泛应用于高动态性能和高密度场合[1]。

永磁同步电机矢量控制系统通常采用位置传感器(如光电编码器、霍尔传感器)来获取转子位置，一方面增大了整个系统的体积，另一方面降低了整个系统的抗扰性，使其易因电磁干扰以及恶劣的环境条件产生故障，甚至危及操作者人身安全。无位置传感器控制方案克服了这一缺陷，同时降低了成本，正在成为电机调速方法的重要研究方向。

在永磁无刷电机的无位置传感器矢量控制方案中，准确的转子实时位置信息尤为重要。PMSM的反电动势包含了转子位置和速度信息，因此基于反电动势的估计方法被广泛使用，如卡尔曼滤波法[1-2]、模型参考自适应法[3-4]、滑模观测器法[5]。其中滑模观测器法具有结构简单、鲁棒性强、对参数不敏感等特性，因此常被实际应用于PMSM的驱动控制中。

然而，滑模变结构方法因其时间和空间的滞后特性将会使系统产生抖振现象，估算结果含有高频振荡噪声。并且，为了实现估计误差的快速收敛以及满足Lyapunov稳定性条件，滑模变结构方法中的切换增益需要足够大，继而加剧了抖振现象[2]。

人工神经网络(ANN)可以在不需要确定系统精确数学模型的前提下实现准确的状态估计[8]。人工智能特点之一就是其学习过程。基于此，有一些方法直接将电机参数(如α-β坐标下的电流、电压)作为神经网络的输入[9]，电机转速或转子位置作为神经网络的输出来实现永磁无刷电机的无传感器控制。这种方法利用了神经网络的自学习能力，但依赖电机数据采样进行离线训练，并且结构复杂，设计和调试难度大，难以应用到实际操作中。

为了减弱上述滑模观测器在应用中的抖振问题，以及简化基于神经网络控制方案的系统结构，提出一种利用RBF神经网络的自学习能力动态调节滑模观测器的切换增益的方法，即设定神经网络的输入为传统滑模估计方案中的电流估计误差，输出为滑模增益，从而使估计模块能够获得更准确的位置和速度估计。为了避免神经网络的离线训练对训练数据的依赖以至产生过拟合，同时降低学习的时间成本，并提高神经网络在实时工作中的鲁棒性，本文方法将网络的学习和运行过程进行了结合，使得网络参数能够在工作过程中进行适时调整。分析及仿真实验表明，该方案有效减弱了滑模变结构方法中的抖振现象，为电机的矢量控制提供更准确得转子位置信息，保证了系统稳定性和鲁棒性。

1 永磁同步电机的数学模型

永磁同步电机在静止α-β坐标系下的数学模型为

(1)

其中，

(2)

式中,iα,β为相电流；uα,β定子电压；Eα,β为反电动势；R为绕组电阻；L为定子电感；ωe为电角速度。

2 无传感器控制中的观测器设计

2.1 基于滑模观测器的静子电流观测器

基于上述PMSM模型的观测器可以写为

(3)

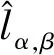
式(1)、式(3)两式相减，可以得到电流误差方程：

(4)

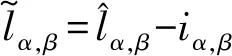
滑模控制律设计为

(5)

式中,KSW为滑模观测器切换增益；sgn(x)为符号函数。

选择滑模面为：

(6)

当观测器状态保持在滑模面上时，此时的控制量可以看作等效控制量。可得：

(7)

因此:

(8)

实际控制输出量是一个有高频扰动的不连续切换控制信号。因此，有必要添加一个额外的低通滤波器(LPF)来从中提取连续的反电动势(back EMF)估计量。同时，基于估算公式(式(8))，还需要添加一个角度补偿来弥补低通滤波器产生的相位延迟：

(9)

式中，ωc为低通滤波器的剪切频率。并且，为减小抖振问题，采用sigmoid函数代替传统的开关函数sgn(s)：

(10)

式中，a为可调参数。

2.2 观测器稳定性分析

下面将由Lyapunov稳定性理论证明如下结论：系统在控制律(式(5))的作用下能够在有限时间内达到滑模面(式(6))，并保证滑模面是渐进稳定的。

证明：定义Lyapunov函数：

(11)

其中，S(x)=[Sα(x)Sβ(x)]。则：

(12)

将式(3)、式(6)带入式(12)并整理可得：

(13)

KSW>Max(eα,eβ)

(14)

因此，为了保证观测器稳定，由RBF神经网络输出的增益KSW与α、β轴的反电动势相比要足够大。

3 RBF神经网络-滑模观测器

RBF神经网络是一种三层前馈网络，即输入层、隐含层、输出层，网络结构简单[11-13]。它也是一种局部逼近的网络，且具有良好的泛化能力。把切换函数作为RBF网络的输入，滑模控制器作为RBF网络的输出，利用神经网络的学习功能，可实现单输入单输出的神经滑模控制[8]，即用神经网络动态调节滑模观测器中的输出切换增益。

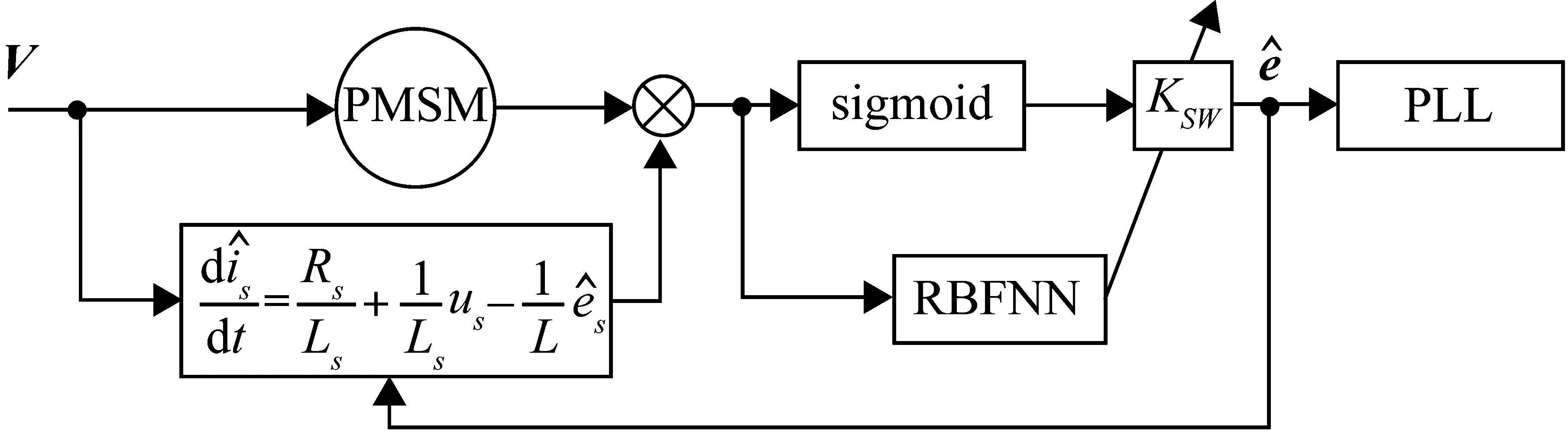
图1 RBF神经网络与滑模观测器结构

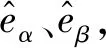
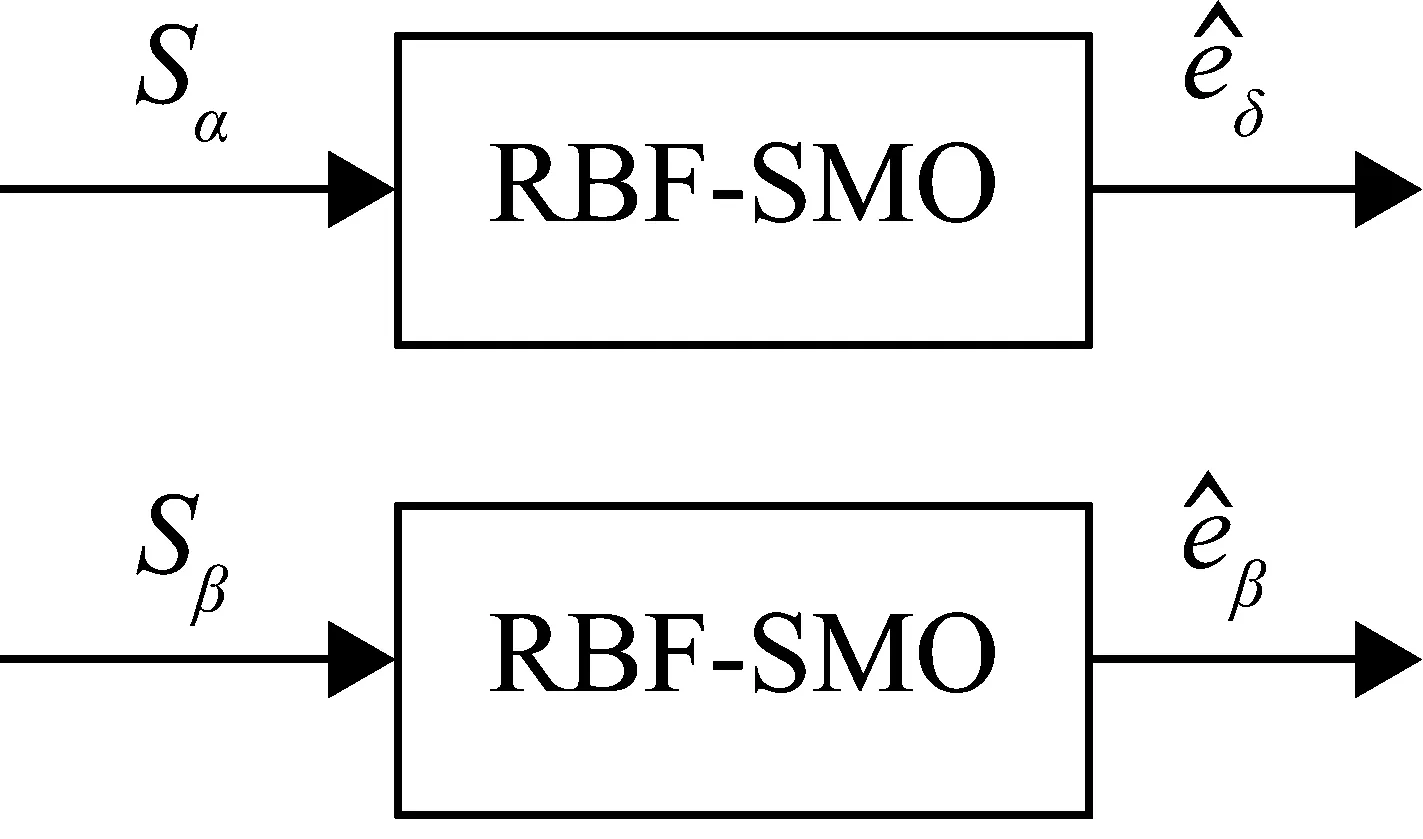
图2 RBF网络-滑模观测器输入和输出

所设计的RBF神经网络中，输入层有一个参数，即电流误差；隐层有5个神经元；输出层有一个参数，即|KSW|。RBF神经网络的初始权值随机选定，工作过程中，每个神经元的输出由前一层神经元对应的权值决定。

本文选择高斯函数作为激励函数：

(15)

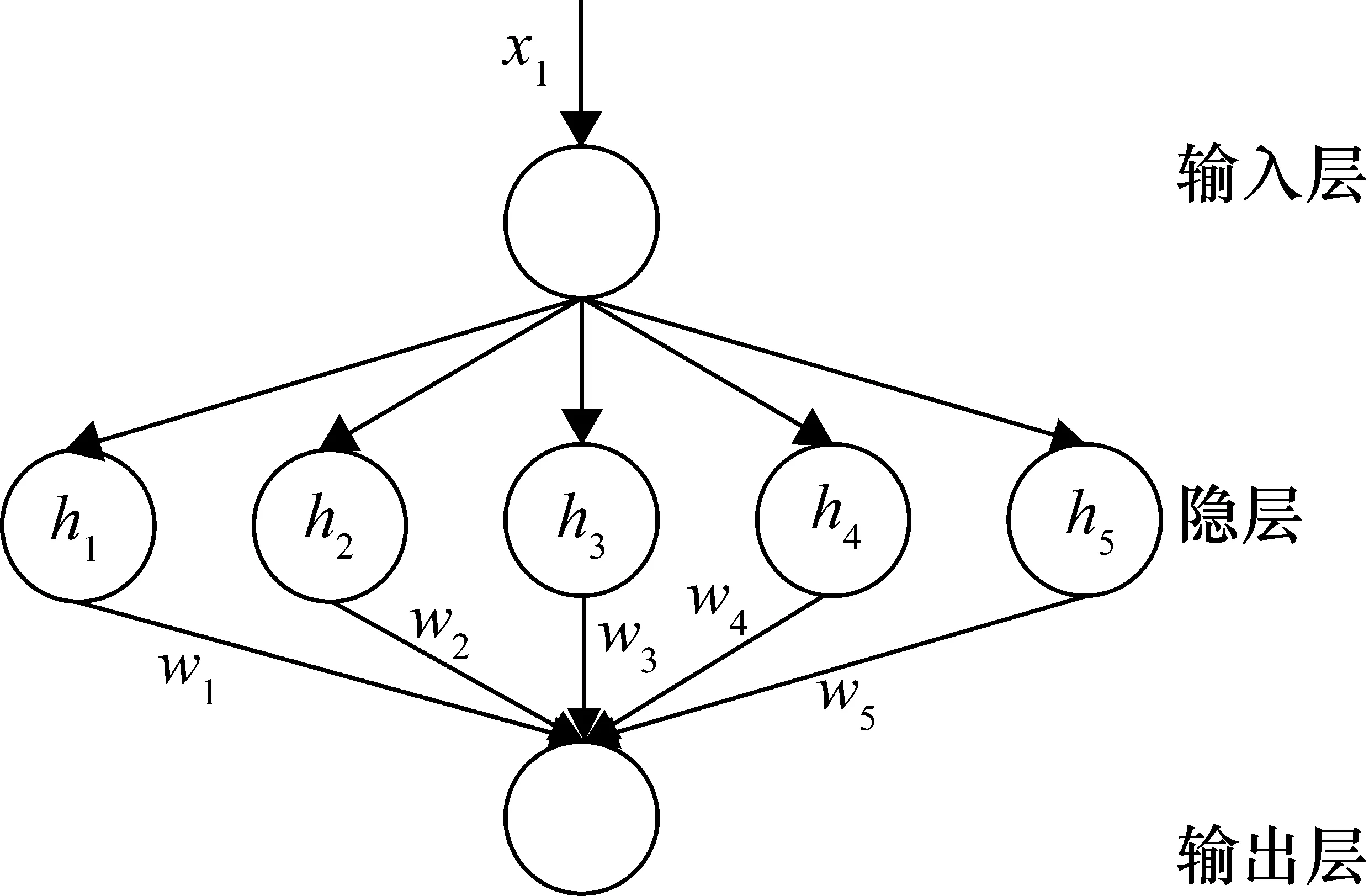
图3 RBF神经网络结构图

式中，X即网络输入，径向基函数向量为H=[h1,h2,…,h5]T，i即网络隐含层第i个神经元，mi为神经元i的中心，σi为神经元i的宽度。

神经网络输出的绝对值是切换函数的增益：

K=|WTh(x)|

式中，WT为神经网络权值;h(x)为高斯核函数输出。

神经网络中误差函数选择为

根据梯度下降理论，神经网络的权值变化公式为

(16)

解之可得：

(17)

式中，C为常数。于是：

(18)

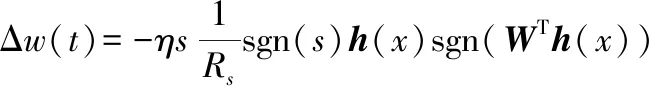
(19)

权值替换公式为：

w(t)=w(t-1)+Δw(t)+α(w(t)-w(t-1))

(20)

式中，α为惯性系数，α∈(0，1)；η为学习速率，η∈(0，1)。神经网络通过以上权值更新公式实时、动态调节输出增益，保证滑模面的渐进稳定性，使得估计的反电动势更准确。

4 仿真结果及分析

为了验证上述RBF-SMO方法的有效性，采用Matlab/Simulink仿真分析工具来建立永磁同步电机控制模型，控制框图如图4所示，电机相关参数见表1。

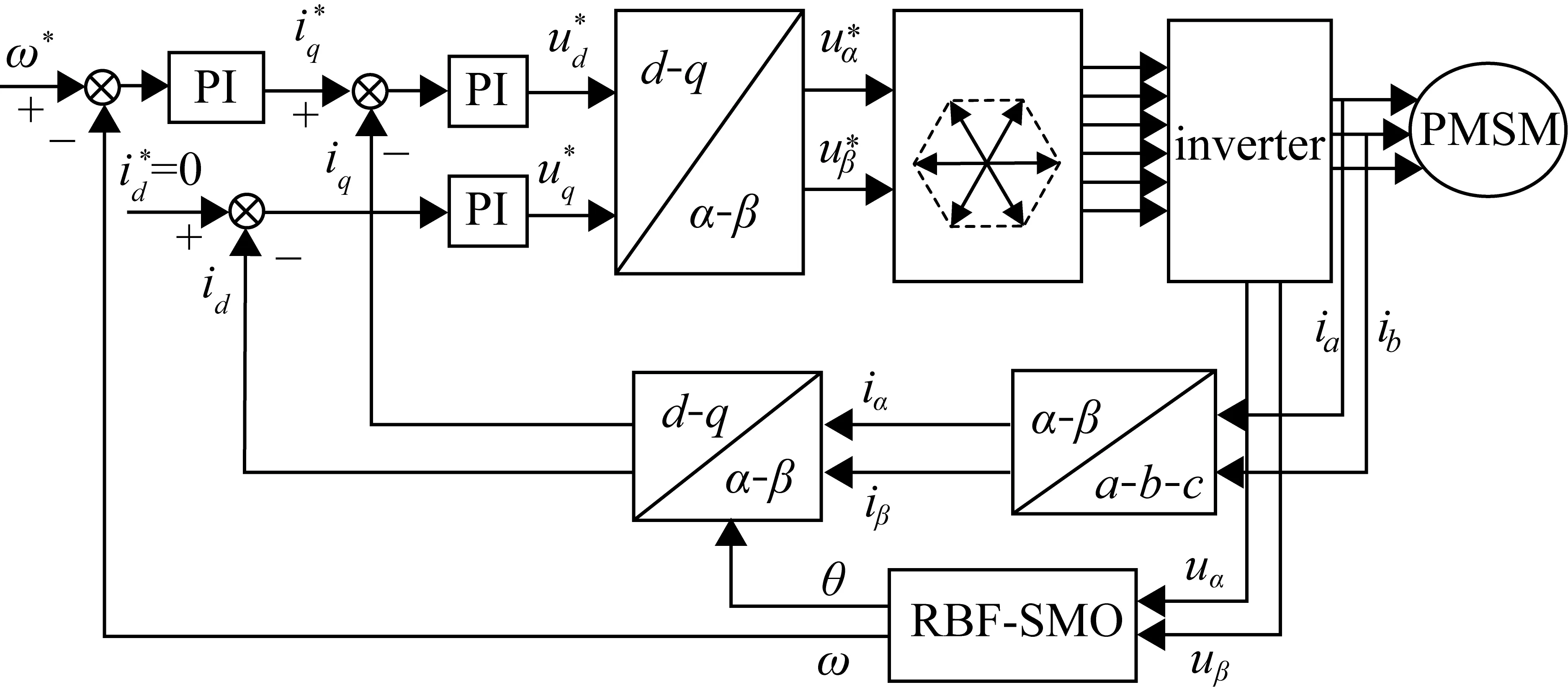
图4 Simulink仿真结构框图

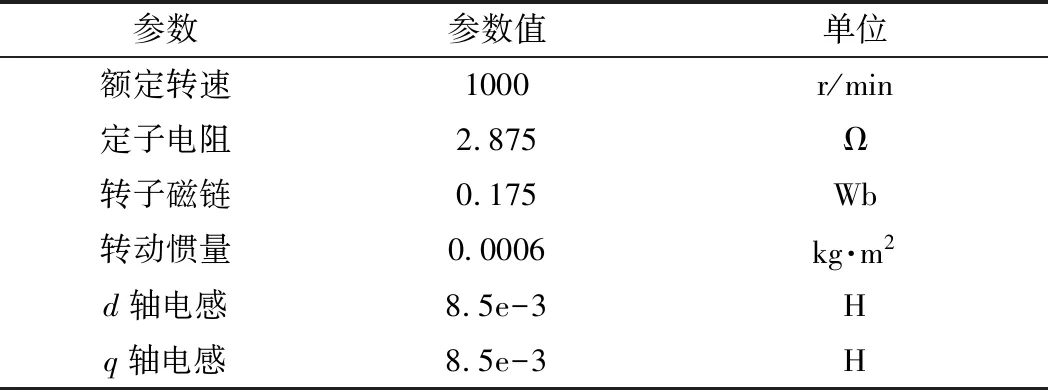
参数参数值单位额定转速1000r/min定子电阻2.875Ω转子磁链0.175Wb转动惯量0.0006kg·m2d轴电感8.5e-3Hq轴电感8.5e-3H

仿真模型中速度环调节器PI参数为Kp=1,Ki=0.2,两个电流环PI参数都为Kp=17,Ki=5750。电机设定转速为1000 r/min。

仿真实验将把本文的RBF网络-滑模观测器方法和传统滑模观测器方法(分别简写为SMO和RBF-SMO)对于电机相关参数的估计值分别与电机参数实际值进行对比。在整个永磁同步电机的控制系统中，由于模块间不可避免的耦合关系，SMO和RBF-SMO的输出都将通过影响电机的实际运行参数间接地影响两个模块各自的输入，而所提出方法的有效性可以通过整个系统的运行性能来验证。因此参照图4所示仿真框图中RBF-SMO模块的输入和输出，以下对于仿真结果的分析讨论将重点展示输入的反电动势和输出的位置及速度估计。其中，为方便观察，反电动势和角度单位均采用标准化处理，其中角度映射范围为(0,2π)。

两种方法估计的α轴、β轴反电动势及其局部放大图分别如图5和图6所示。

图5和图6为SMO方法和RBF-SMO方法对于电机反电动势(α轴和β轴)的估计对比图。从图中可以看出，利用神经网络的学习和逼近能力，所提出的方法有效减弱了滑模观测器的抖振，使得估计的反电动势抖动更小，更接近真实值。同时，准确的反电动势估计值也将使速度跟踪更精确。

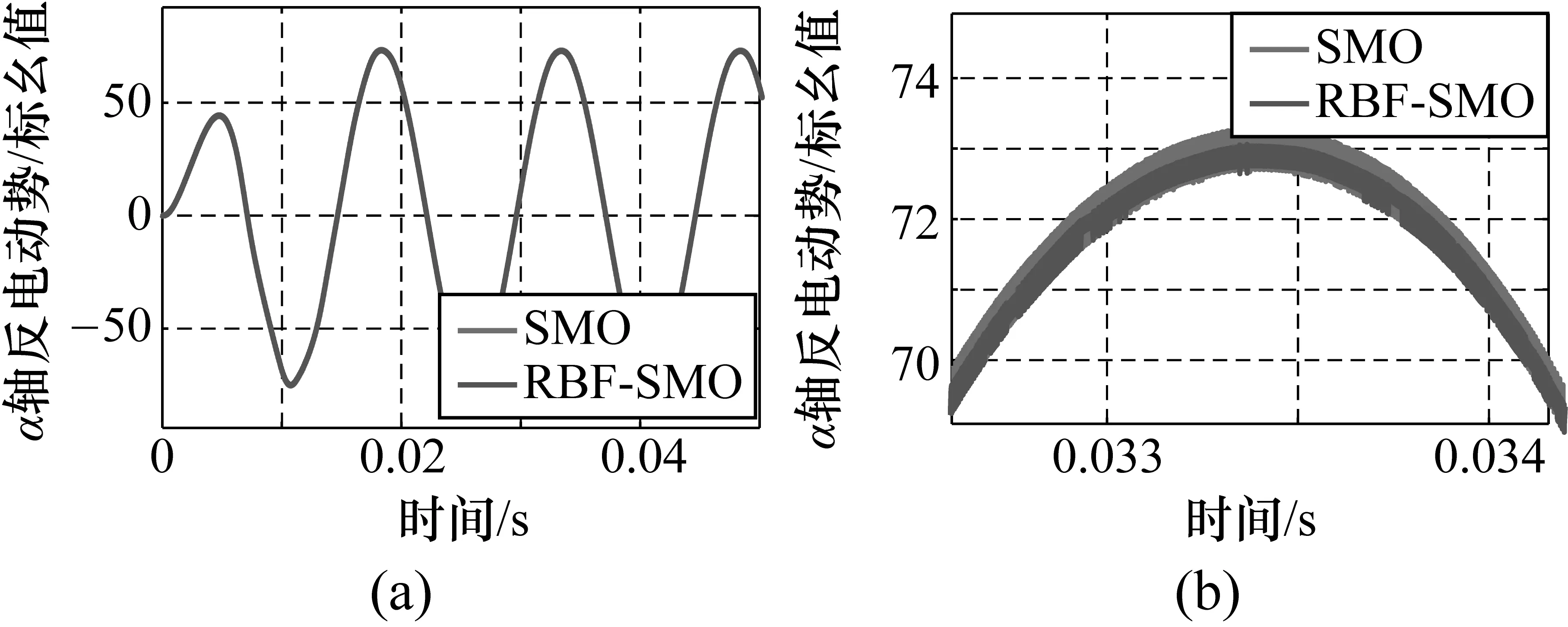
图5 估计反电动势vα及其局部放大图

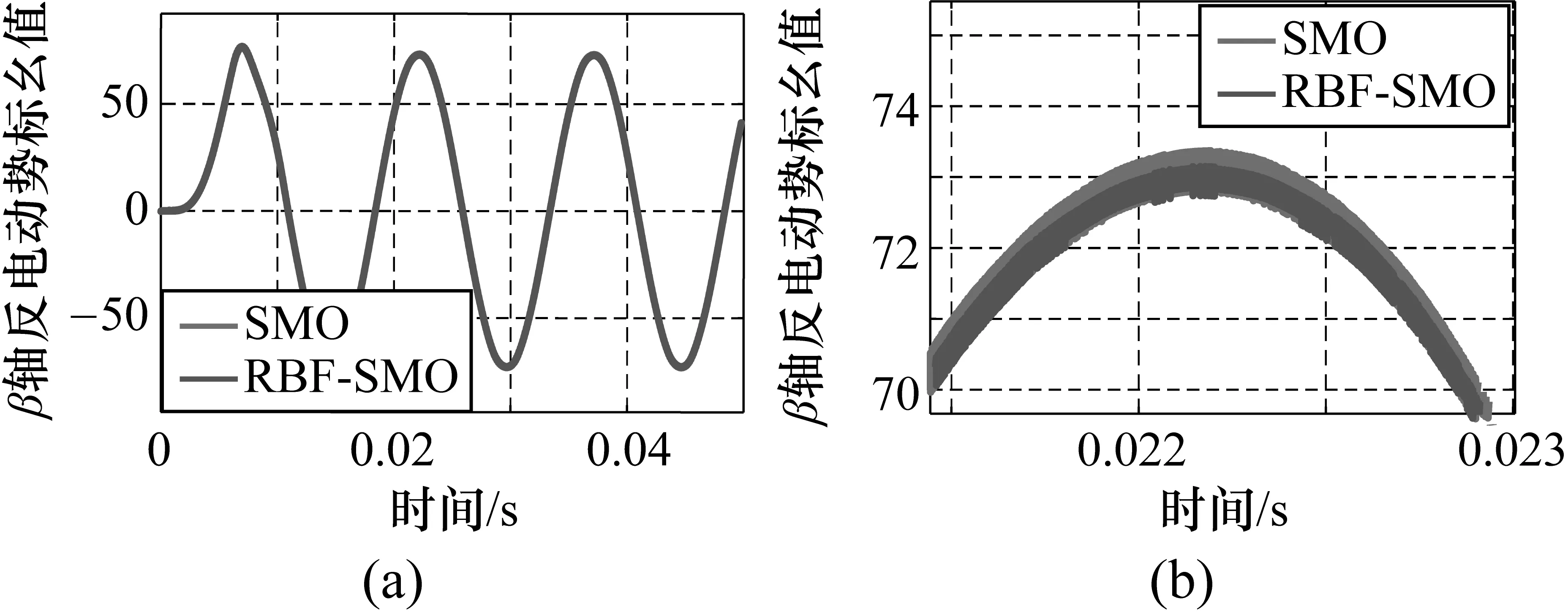
图6 估计反电动势beta及其局部放大图

两种方法对转子位置及速度的估计及其局部图分别如图7和图8所示。

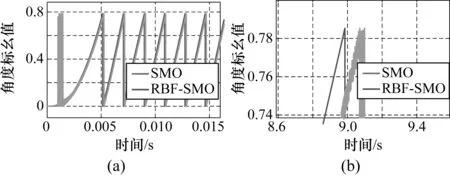
图7 转子估计位置及其局部放大图

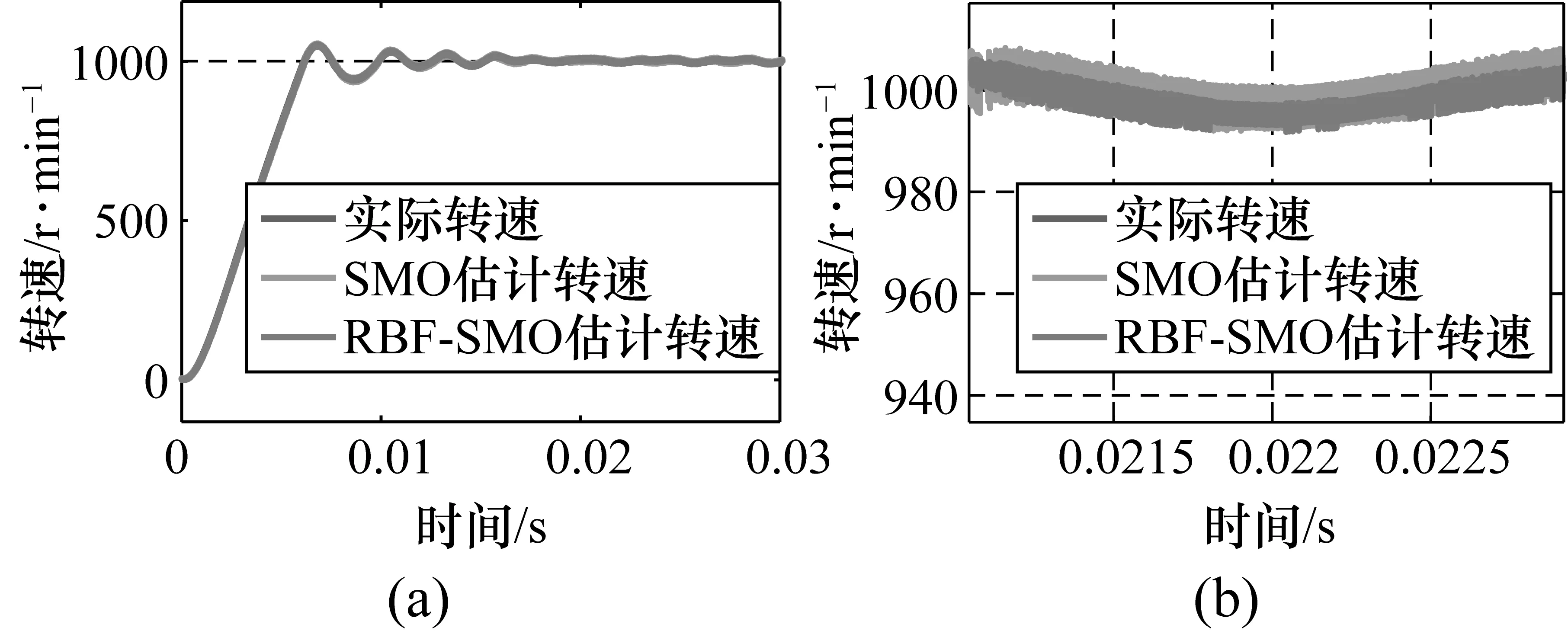
图8 估计转速及其局部放大图

图7(b)为传统SMO方法和RBF-SMO方法对转子位置估计的对比图。从图中可以看到，RBF-SMO方法对于转子位置的估计与转子实际位置之间的误差相对传统SMO方法更小，提供的位置信息更精确。如前所述，这样的效果当是由对反电动势更加精确的估计所致。精确的位置估计必然带来更精确的速度估计，进而如图8(b)所示，基于所提出的RBF-SMO方法所提供的转子速度相对于传统SMO方法抖动较小，最终使得电机的运转更加平稳。

5 结束语

本文针对永磁同步电机提出一种使用RBF神经网络调节滑模观测器增益的无传感器位置辨识方法，并对其估计效果进行了分析；其中，通过Lyapunov稳定性理论对该控制器的稳定性进行了证明。仿真结果表明，所提出的方法能够有效减弱传统滑模方法中的抖振问题，进而提供更准确的转子位置信息，增强系统鲁棒性。实验结果更进一步印证，该方法可经适当简化应用于实践。