基于多尺度加权排列熵的管道泄漏检测

(浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

管道运输是物料长距离运输方式之一，特别是油气的长距离运输[1]。但由于管道腐蚀、地质灾害、第三方破坏等多方面因素，管道泄漏现象仍时有发生。管道泄漏不仅会造成重大的经济损失，甚至会产生严重的生产事故[2]。2011年12月，珠海横琴天然气处理终端附近海底天然气管线出现泄漏，天然气净产量日损失达4.53×106 m3[3]。2013年11月，青岛东黄输油管道原油泄漏现场发生爆炸，造成63人遇难、156人受伤，直接经济损失7.54亿元[4]。因此，建立高效的管道泄漏检测系统，能够最大程度地避免不必要的经济损失以及人员伤亡。

目前，针对管道泄漏检测问题，学者已取得较多研究成果。典型的管道泄漏检测方法，包括负压波法[5]、动态压变法[6]、音波法[7]等。这些方法从泄漏机理出发，通过分析管道压力、噪声等变量的变化，来检测管道是否出现泄漏。此外，针对管道信号的非平稳性，将采集到的压力、噪声等信号作为时间序列，通过分析可知，该时间序列的异常模式也可用于判断管道泄漏。文献[8]考虑到泄漏声源信号与非泄漏声源信号的特征差异，将获得声源信号的自相关函数作为特征提取对象，然后进行近似熵计算，根据真实产生的泄漏声信号具有“不可重复性”，从而识别泄漏是否发生。文献[9]采用总体局部均值与Kullback-Leibler divergence相结合的方法分解筛选出包含主要泄漏信息的特征分量，在此基础上采用基于过完备字典稀疏表示的分类方法实现泄漏孔径的识别。文献[10]提取管道压力信号的特征熵作为输入向量，选取支持向量机作为分类器，通过粒子群算法来优化参数，将优化后的支持向量机与特征熵相结合，来完成对管道泄漏的判断。文献[11]通过提取固定长度的压力序列作为时间序列，计算每个时间序列的加权排列熵值，通过加权排列熵的变化来判断管道的泄漏。

排列熵不需要考虑时间序列具体数值的大小，而是基于相邻数据的对比，获取时间序列的特征信息。相对其他熵而言，排列熵能够放大时间序列的微变信号，算法简单，具有较好的抗噪性能，被广泛用于时间序列复杂度的分析[12-17]。在排列熵只考虑了时间序列的序数结构的情况下，Fadlallah[18]等人还考虑了时间序列的幅值信息，提出了加权排列熵。然而，上述方法都只是在单一尺度上衡量时间序列的随机性和动力学突变，所能表征的时间序列复杂度有限。因此，Aziz[19]等人在单一尺度的排列熵基础上提出多尺度排列熵，用于衡量不同尺度下时间序列的复杂性。与单尺度排列熵相比，多尺度排列熵具有更好的鲁棒性[20]。

本文基于管道压力信号时间序列，通过移动窗方法构建固定长度的时间序列，对其进行多尺度加权排列熵分析。以多尺度加权排列熵是否发生跳变作为判定管道泄漏的指标，实现管道的泄漏检测。实验结果验证了所提算法的有效性。

1 多尺度加权排列熵

1.1 排列熵方法

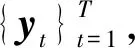
(1)

式中，m为嵌入维数；τ为延迟时间。

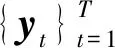
{yi+k1-1≤yi+k2-1≤…≤yi+km-1,1≤k1,k2,…,km≤m}

(2)

每一行重构分量按升序排列后可以得到一组符号序列πi=[k1,k2,…,km]。m个不同的符号总共有m!种符号序列，计算每一种符号序列出现的概率P(πj)：

(3)

按照香农熵的形式，该时间序列的排列熵H(m,τ) 定义为：

(4)

从式(4)中可以看出排列熵的取值范围为[0,lnm!]。由此，可得归一化的排列熵，即

HP=H(m,τ)/ln(m!)

(5)

由排列熵的定义可知，排列熵的原理在于不考虑数据具体值，而是通过序数模式来表现时间序列的复杂性，算法简单，具有较强的抗噪性能。

1.2 多尺度排列熵方法

根据定义(3)可知，一般的排列熵方法只保留了时间序列的序数结构，而忽略了相同序数之间的幅度差。因此，文献[18]提出了加权排列熵，即在一般排列熵的基础上考虑了时间序列的幅值信息。然而，加权排列熵也只是在单一尺度上检测时间序列的复杂度和动力学突变。在反映管道压力信号时间序列特征细节方面仍存在一定的不足，因此提出了一种基于多尺度加权排列熵的泄漏检测方法。

多尺度加权排列熵的原理就是将时间序列进行粗粒化处理，然后分别计算各个尺度下的加权排列熵值。多尺度加权排列熵的计算步骤如下所示。

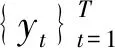
(6)

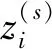
② 根据排列熵的操作步骤，考虑了时间序列的幅值信息，给每个重构分量添加一个加权系数：

(7)

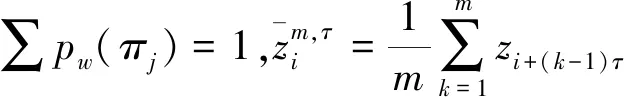
(8)

(9)

2 基于多尺度加权排列熵的管道泄漏检测方法

由于多尺度加权排列熵的大小反映了时间序列的复杂性和随机性。当管道处于正常状态时，压力信号的随机性是最大的，多尺度加权排列熵的值较大，此时熵值会在某一范围内上下波动，而当管道突然发生泄漏时，压力开始下降，时间序列复杂度降低，熵值会发生跳变，因此可以构建管道正常运行时熵值的统计量，结合休哈特控制图确定其控制限，H落在区间[uH-3σH,uH+3σH]内的概率为99.73%，uH、σH分别为构建的统计量的均值和方差，将多尺度加权排列熵是否在控制限内波动作为管道泄漏的指标。

为了保证检测的实时性，采用最大重叠的移动窗口法选取，即下一个时间序列是上一个时间序列向后移动一个单位，利用多尺度加权排列熵将移动窗内的时间序列进行粗粒化处理，然后计算每个粗粒化后的时间序列的熵值，具体步骤如图1所示。

① 采集长度固定为T的实时压力序列yt;

② 将yt进行粗粒化处理，得到新的时间序列zt；

③ 选择合适的延迟时间τ和嵌入维数m计算当前时间序列的熵值H(m,τ)；

④ 舍弃时间序列的第一个压力值，取最新时刻的压力值，组成一个长度为T的新的时间序列;

⑤ 获取管道正常运行时熵值的统计量，通过休哈特控制图确定其控制限;

⑥ 比较当前时刻的熵值与前一时刻的熵值，当多尺度加权排列熵值发生大的跳变不在控制限内时，判定泄漏发生;

⑦ 如果泄漏没有发生，则重复步骤①～步骤⑥。

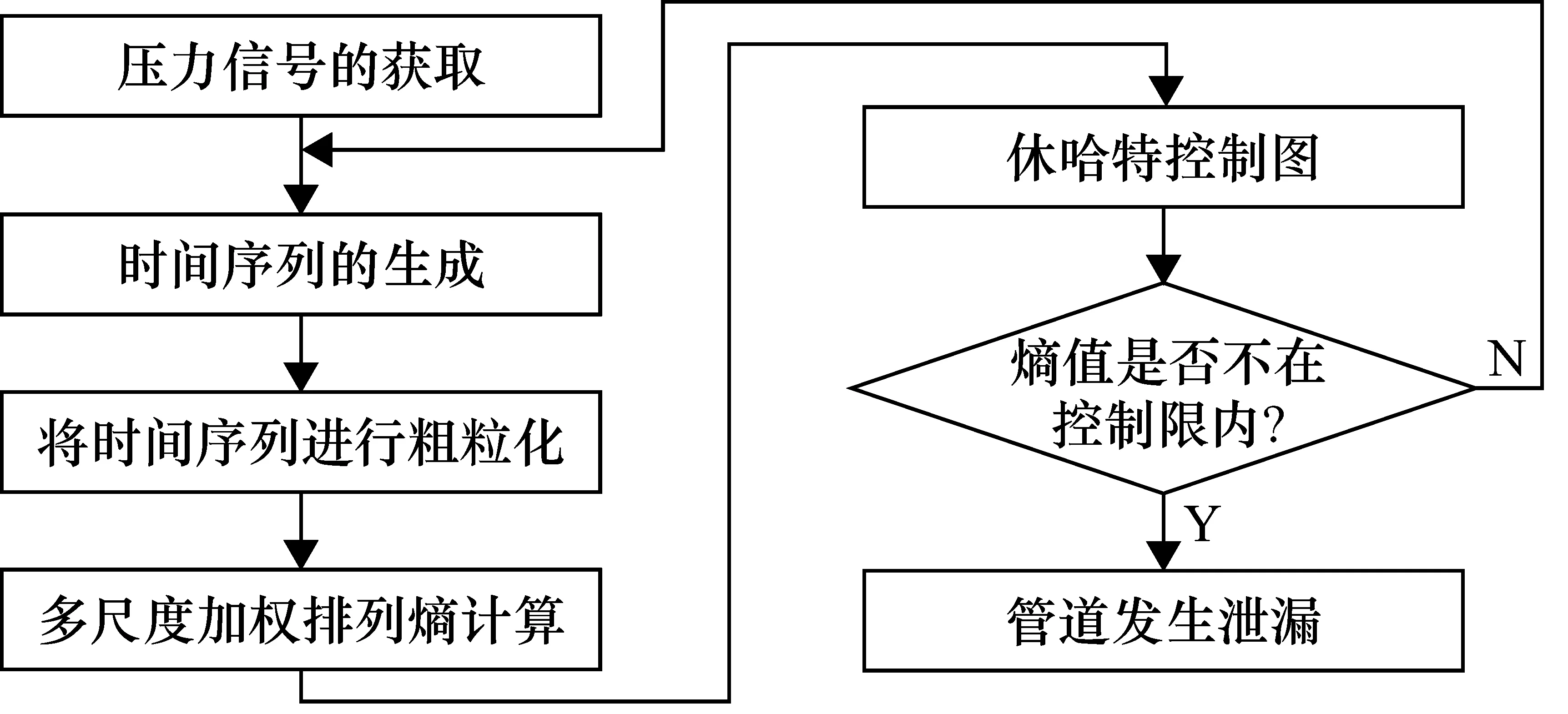
图1 管道泄漏检测流程图

3 结果分析

3.1 实验装置介绍

实验装置示意图如图2所示。管道的总长度为200 m，管道内传输的介质为水，在管道的进口与出口处各放置一个智能数字压力传感器，可以对压力信号进行滤波、放大、A/D转换、校正，精度可达0.1%FS，适用于流体的超高精度压力监测[21]。传感器的采样频率为100 Hz，在管道上设立3个泄漏点，泄漏点的泄漏孔的直径分别为4、8、20 mm，与主管道的截面积之比分别为(百分比)：0.07%、0.28%、1.78%，通过控制阀门的开关来模拟管道的泄漏。管道进口的压力值由实验台进行控制，范围为0～0.7 MPa。装置现场图如图3所示。

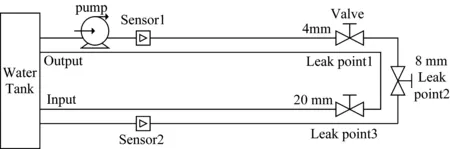
图2 管道布置

图3 现场实验台

3.2 多尺度加权排列熵参数选择

根据多尺度加权排列熵的定义和计算步骤[20]可知，数据长度、嵌入维数和延迟时间是影响多尺度加权排列熵算法的主要参数。将多尺度加权排列熵应用至管道压力信号时间序列中，如果嵌入维数过小，重构的序列中包含太少的状态，算法将失效，不能检测到时间序列的突变，而嵌入维数过大，相空间的重构将会均匀化时间序列而难以观察压力信号的细微变化，计算也会变得耗时。一般来讲，嵌入维数取3～7。通过对包含泄漏信息的压力信号进行分析，比较不同数据长度、嵌入维数和延迟时间，本文最后选定数据长度T=200，嵌入维数m=3，时延τ=20作为多尺度加权排列熵算法的参数。通过对不同泄漏量下的管道泄漏检测，并与文献[22]所提出的基于小波分析的管道泄漏检测方法进行对比，以验证所提出的算法的有效性。

3.3 结果分析

图4为管道在压力为0.7 MPa、孔1发生泄漏时的原始压力信号时间序列。图4把压力序列分为5个阶段，分别为泄漏发生前、泄漏发生时、泄漏发生后、管道恢复正常时、管道恢复正常后。图5(a)为尺度因子为1的管道压力信号时间序列的多尺度加权排列熵值曲线，即单尺度加权排列熵曲线。图5(b)、图5(c)分别为尺度因子为4、10时的管道压力信号时间序列的多尺度加权排列熵值曲线。从图5可知，当管道压力在正常范围内波动时，多尺度加权排列熵在控制限内波动，尺度因子越大，波动越小，鲁棒性越好；当泄漏发生和管道恢复正常时，压力信号时间序列的复杂度降低，熵值发生巨大的跳变。同时，对比图5(a)～图5(c)可知，随着尺度因子的增大，管道泄漏发生时多尺度加权排列熵的跳变更明显，更有利于判断泄漏是否发生。采用文献[22]和文献[23]所提出的方法进行小波去噪后，再采用邻域差值法得到的差值曲线如图5(d)所示，该方法也可检测到管道泄漏。

图4 0.7 MPa下孔1发生泄漏的管道压力曲线

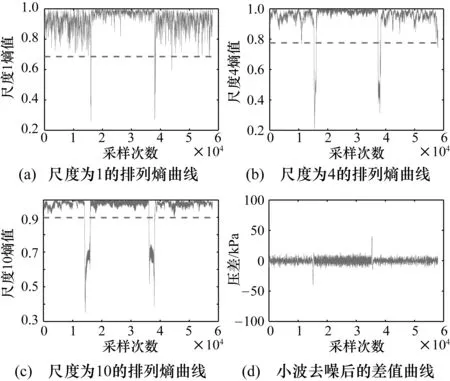
图5 0.7 MPa孔1发生泄漏时的多尺度加权排列熵曲线

图6、图7分别为管道在压力0.7 MPa下、孔2和孔3发生泄漏时的多尺度加权排列熵曲线，从中可以看出多尺度加权排列熵在不同的泄漏情况下对管道的泄漏检测都有着很好的效果，且随着尺度因子的增大，效果更加明显。采用最大重叠的移动窗口法获取时间序列，因此可以将多尺度加权排列熵曲线与控制限的交点作为泄漏发生的时间。为了进一步比较所提方法的性能，表1列出了不同泄漏量下，所提方法与文献[22]所提方法检测到的泄漏发生时间。从表1中可以看出，在不同泄漏下，所提出的算法检测到泄漏的时间先于文献[22]的方法，具有更好的实时性。

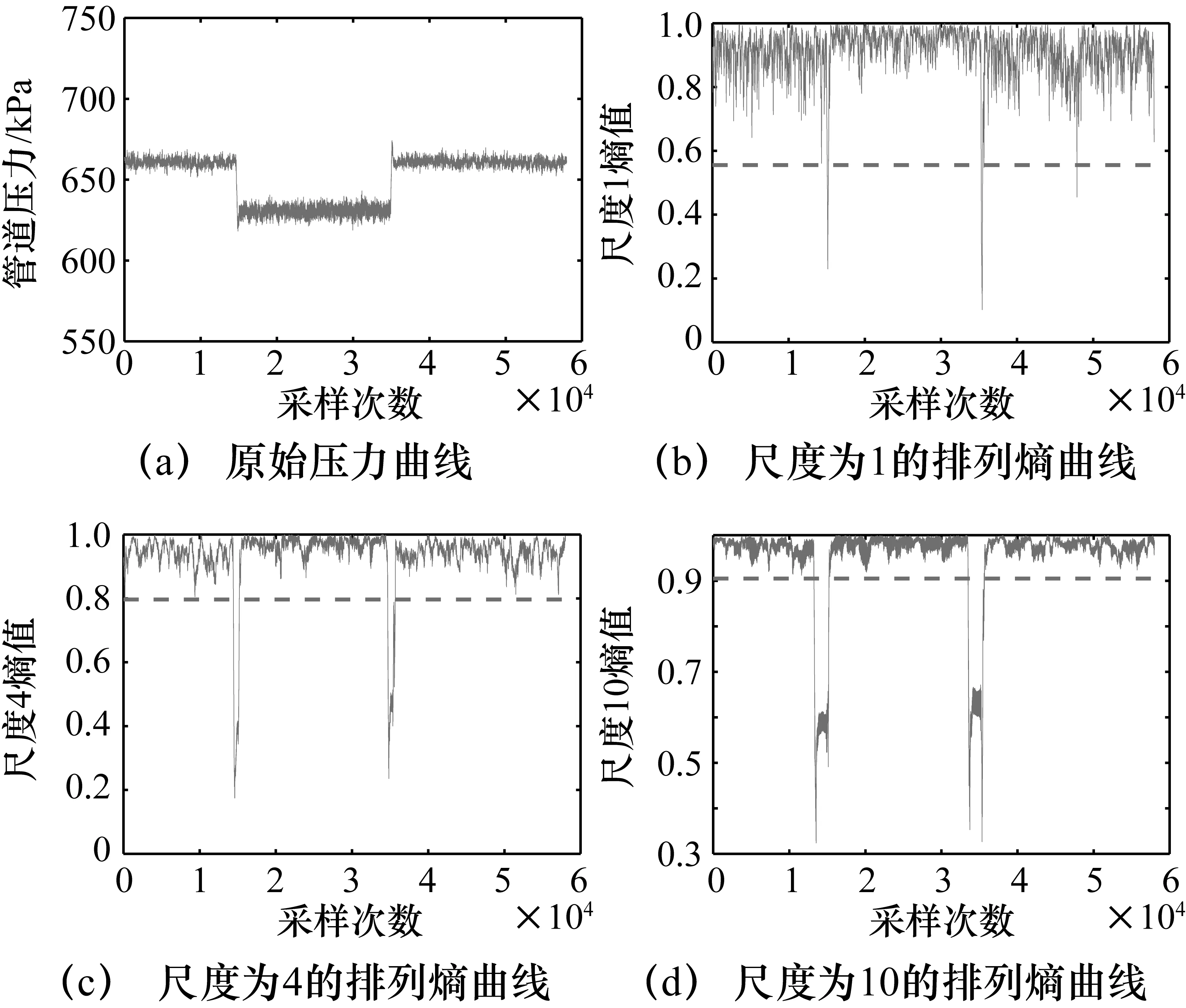
图6 0.7 MPa孔2发生泄漏时的多尺度加权排列熵曲线

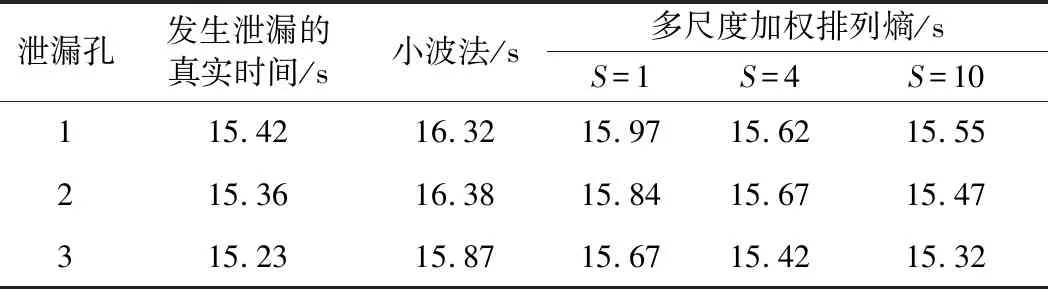
泄漏孔发生泄漏的真实时间/s小波法/s多尺度加权排列熵/sS=1S=4S=10115.4216.3215.9715.6215.55215.3616.3815.8415.6715.47315.2315.8715.6715.4215.32

图8为管道在压力为0.1 MPa、孔1发生泄漏时的原始压力信号时间序列。如图8所示，此时管道的泄漏量较小，且由于噪声和外界的干扰，泄漏的信号变弱，不能有效地提取出泄漏信号的特征信息。对比此时的多尺度加权排列熵曲线，如图9所示。图9(a)为尺度因子为1时的熵值曲线，即单尺度加权排列熵曲线，从图中可以看出此时正常情况下熵值的波动较大，当泄漏发生时熵值的跳变不太明显，无法很好地判断泄漏的发生。对比图9(b)、图9(c)可知随着尺度因子的增大，管道没有泄漏时熵的波动减小，且一直处于较大值，当管道发生泄漏时熵值发生明显的跳变。图9(d)为文献[21]所提方法得到的邻域差值曲线。对比两个方法可以看出多尺度加权排列熵对管道的微小泄漏有着很好的效果。

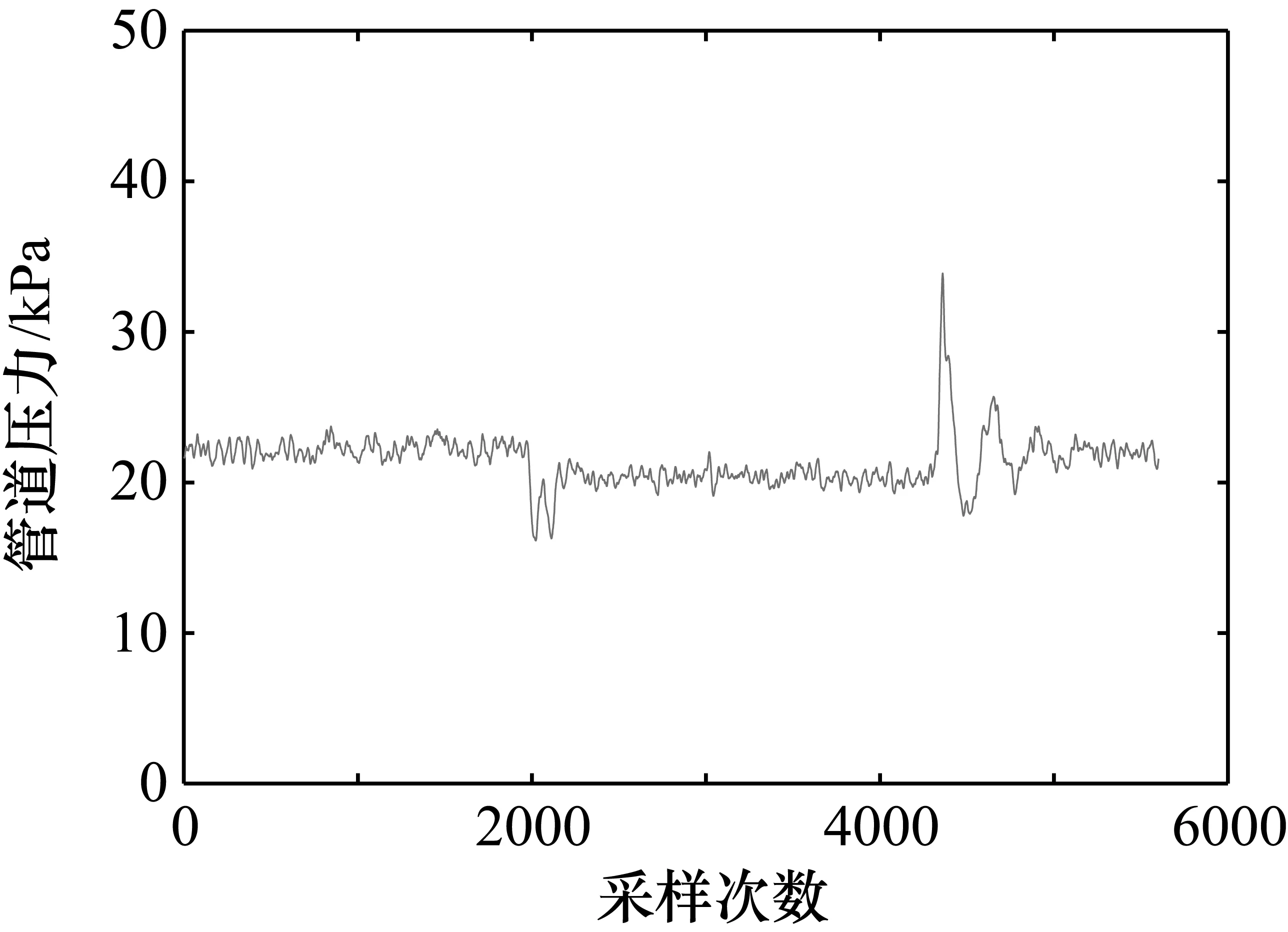
图8 0.1 MPa下的管道压力曲线

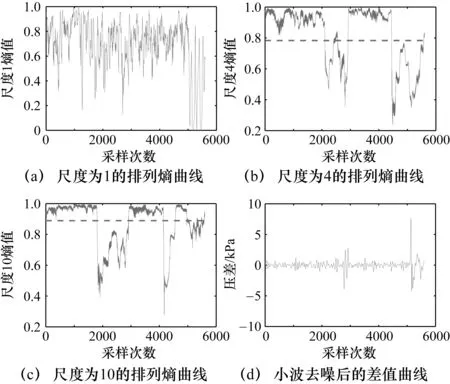
图9 0.1 MPa下的多尺度加权排列熵曲线

4 结束语

基于多尺度加权排列熵，通过对管道内的压力信号时间序列进行分析，提出了一种新的管道泄漏检测方法，利用多尺度加权排列熵值的跳变来识别管道状态的变化。通过搭建实验装置对所提出的方法进行验证。结果表明，所提出的方法能有效地检测管道的泄漏，为管道的泄漏检测提供了一种新的思路和手段。