基于单向量S变换的旋转变压器软件解码方法

(1.湖南工业大学 电气与信息工程学院，湖南 株洲 412007； 2.湖南工业职业技术学院 电气工程学院，湖南 长沙 410208)

旋转变压器(以下简称旋变)作为一种位置检测器，因其低成本、强抗干扰能力等优点被广泛地应用于永磁同步伺服系统的电机转子位置和速度的实时测量。然而，旋变输出的是由转子转动位置决定的对输入正弦激励信号调制的两路正交的正弦和余弦模拟信号，从中获取位置和速度信息需要对上述两路模拟信号进行解码。目前的旋变解码方法可以分为基于硬件和基于软件两大类[1]。基于硬件的解码方法一般采用专用解码芯片——旋变数字转换芯片(Resolver to Digital Convertor，RDC)。这种芯片解码精度高，且能够提供旋变所需的激励信号，但其最大的缺点是成本高，一片RDC甚至与旋变的价格相当，因此现在越来越多的研究者寻求低成本的解码方法。文献[1]采用DSP实现对旋变的同步解码，但此方法仅能应用于低速场合。文献[2]在旋变求模运算得基础上进行FPGA纯硬件实现，简化了电机矢量控制系统的硬件和软件。

常用的旋变信号软件解码方法可分为反正切法和角度跟踪法[3](Angle Tracking Observer,ATO)。反正切法由于直接对检波得到的包络信号做反正切运算，当存在噪声干扰时，将得到不稳定的角度解码值，难以用于高精度位置检测和控制系统。文献[4]基于正余弦信号的极性和绝对值提出一种改进的ATO算法，能够实现宽速度范围的软件解码，拓展了ATO解码方法的应用范围。文献[5]提出在输出信号出现幅值偏移的情况下，ATO方法的检测精度会受到较大影响，并利用D-Q变换提出了旋变解码的误差补偿方法。虽然有不少研究者提出了诸如双同步参考结构的ATO解码方法，但实现颇为复杂，实际应用受到限制[6]。

上述旋变解码方法主要集中在时域，虽然具有实时性，但难以兼顾抗干扰性和精确性。旋变信号是非平稳信号，对非平稳信号的分析时频方法在噪声抑制和准确度方面更具优势。但现有的时频分析方法也存在计算量大等问题，基于时频分析工具不完全S变换(Incomplete S Transform,IST)引出单向量S变换(SVST)，用于提取旋变信号的模向量，并通过角度修正算法实现旋变信号的精确解码。

1 单向量S变换(SVST)

1.1 SVST简介

SVST源自S变换[7]，并结合改进S变换[8]和IST思想，在显著减少算法计算量的同时继承了其直观的时频特性和强抗干扰性。近年来，改进S变换和IST主要应用于电能质量扰动检测和分类中[9-14]。针对旋变信号特点，通过计算对应旋变激励信号频率点的一维IST向量，同时引入改进S变换的高斯窗宽调整系数，提出SVST方法，其表达式如式(1)～式(4)[8]：

(1)

(2)

根据卷积定理，式(1)可转换为频域加窗计算。整合调整系数，并写成离散化形式，SVST可写为

(3)

其中，

(4)

式中，n为离散时间序号n=τ/T；N为采样总点数；T为采样周期；l0为旋变信号频率序号l0=f0NT；q为调整系数。由式(3)计算得到的是一维向量，即对应于频率f0的SVST复数向量。

1.2 最优窗宽系数q的选择

由式(3)可知，高斯窗G(m,q)影响SVST检测信号幅值的性能，而用系数q可调整G(m,q)窗宽。图1举例说明了不同的q值对检测信号幅值的影响。图1(a)为时长为0.2 s、幅值为1、频率为52.5 Hz的余弦信号，初始相位π/2，采样频率5 kHz，共1000个采样点。显然上述采样频率不满足同步采样条件，对图1(a)信号做FFT分析会存在频谱泄漏。采用不同的q值对图1(a)信号做SVST得到图1(b)中的不同SVST模向量。

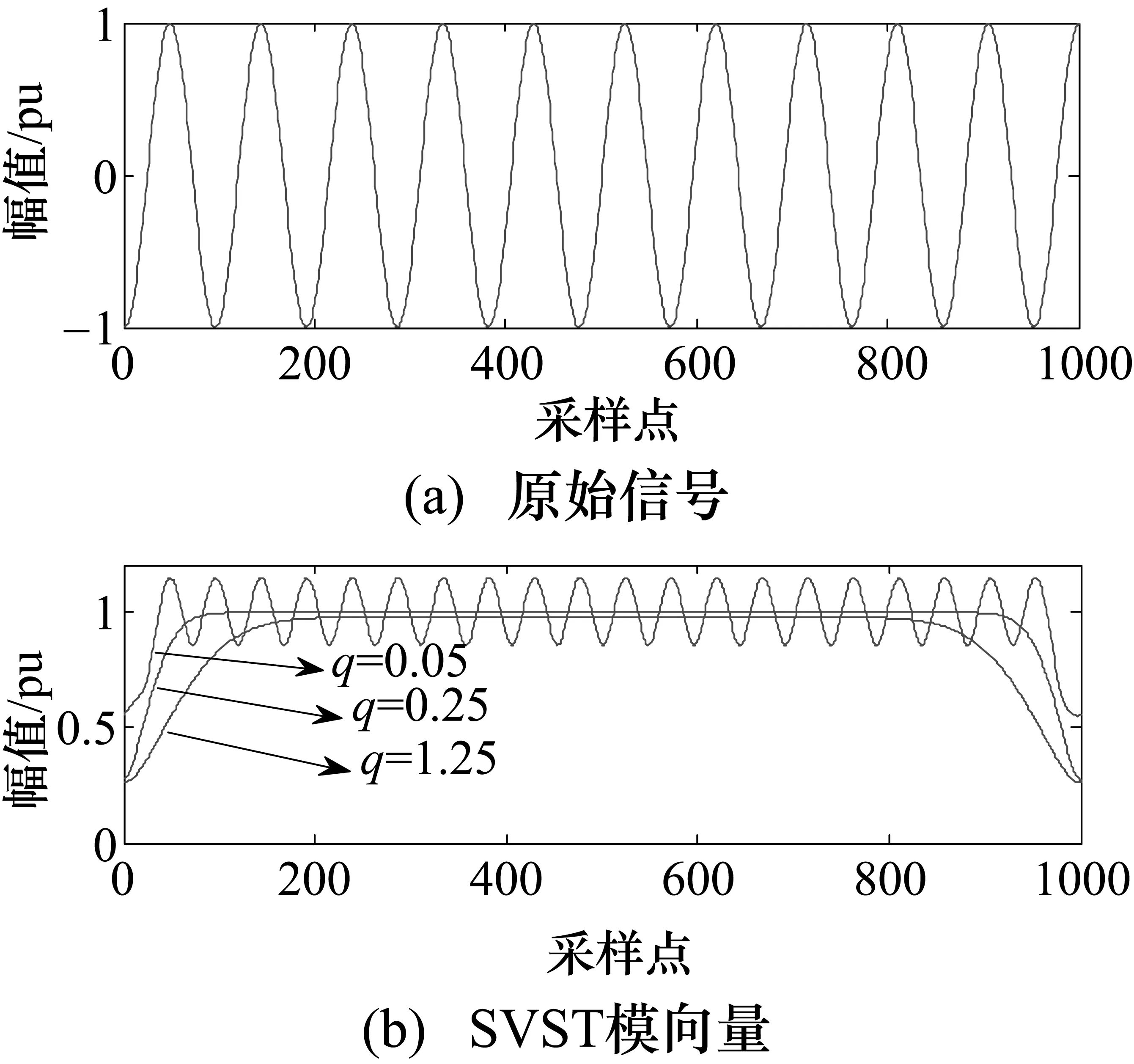
图1 q值对SVST模向量的影响

图1表明，q太小，模向量会出现抖动，失去直接测量性，这是因为SVST运算过程中循环移位再求IFFT，相当于对原始信号乘上一个同频旋转因子，即

(5)

将满足能同时保持SVST模向量平滑性和检测准确性的q值称为最优窗宽因子qr，在图1中qr=0.25，根据式(4)，q值与信号总时长NT成反比，若确定了已知时长为信号Td0的qr0值，对单频率点而言，因l0不变，为保持G(m,q)宽度不变，采用时长为T的qr为：

(6)

1.3 端部效应

在对旋变信号非同步采样时，会造成输出结果端部失真，如图1(b)中模向量两端出现畸变，称为端部效应。端部效应会影响计算输出结果的精确性，故要消除端部效应对计算结果的影响。采用叠接舍去法，即只采用SVST结果中间有效段用于解码计算。如图2所示，若上一次和下一次SVST的幅值为Ai和Ai+1，根据叠接舍去法的原理，将两次计算幅值的端部失真结果舍去，并将两次非失真部分保留叠接作为计算结果，可保证SVST对应原始信号的连续性和解算准确性。

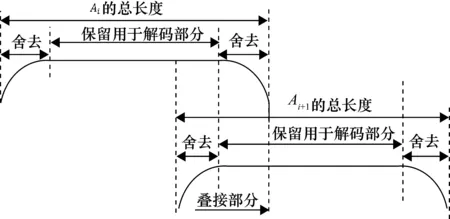
图2 端部效应消除

2 基于SVST的旋变解码方法

2.1 旋变工作原理

旋变作为高精度绝对位置传感器，其输入信号为励磁绕组所产生的激励，输出为由两路测量角度正余弦调幅的模拟信号[15]。旋变信号与转子转角位置满足一定的函数关系，解算该关系可以获取电机的位置信息。图3为简化的旋变工作原理，安装在旋变转子的激励线圈输入激励信号ve产生交变磁场。正交安装在旋变定子的正弦线圈和余弦信号线圈感应激励线圈磁场产生交变电压vs和vc，其幅值与旋变转子位置有关。旋变的两路输出信号的包络被调制为正弦和余弦信号，其数学表达式如式(7)。

(7)

式中，k为旋变的变压比；ω为励磁电压角频率；θ为旋变输出的角度。

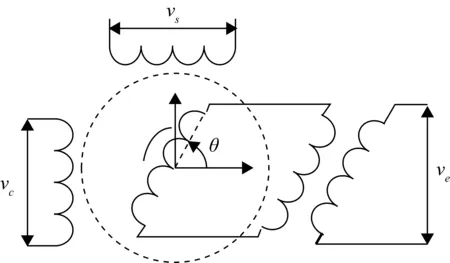
图3 旋变工作原理图

2.2 基于SVST的解码思路

所提出的旋变解码方法如图4所示，其中SVST频率点由ve的FFT频谱峰值确定，图中Find( )函数具有实现查找频谱峰值的功能。对旋变信号vs和vc做SVST后求其模向量，结合反正切和象限区间判断解码旋变的角度值，并完成速度的解算。

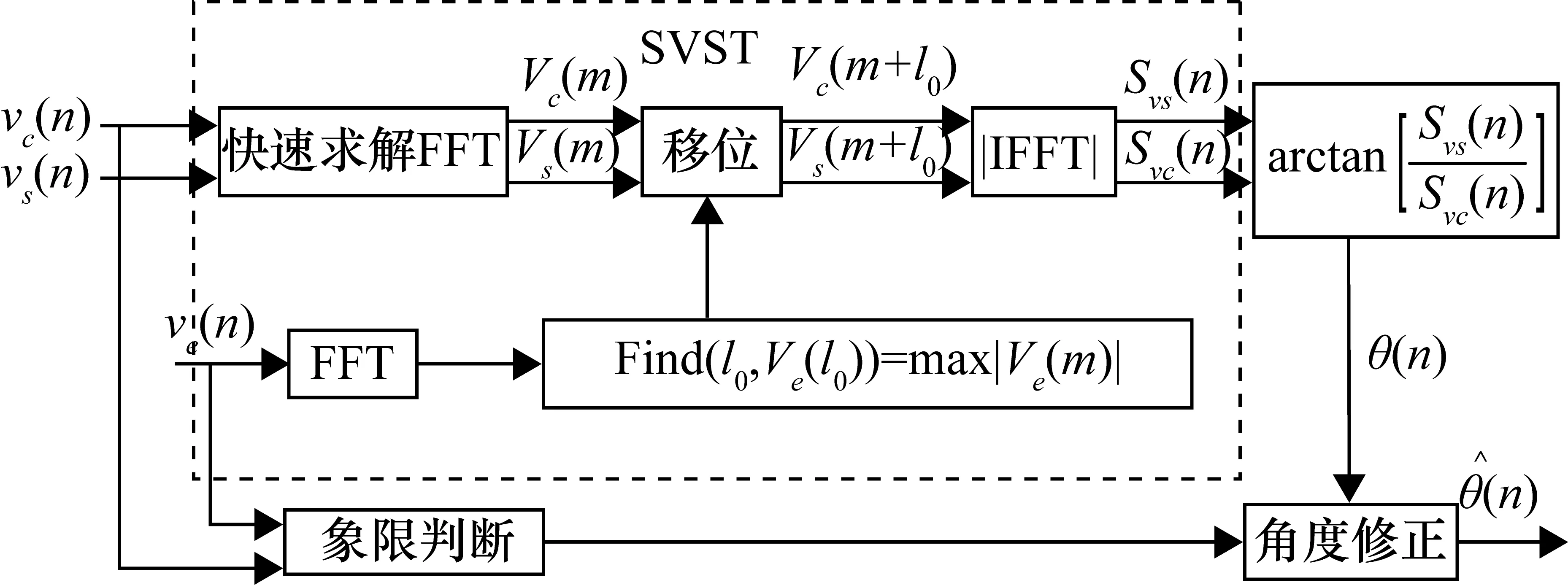
图4 基于SVST的旋变解码原理图

本文旋变解码的具体步骤如下。

① 将两路实信号vs(n)和vc(n)构造成复信号一次求解两路FFT得到Vs(m)和Vc(m)，对Vs(m)和Vc(m)移位加窗后进行IFFT运算，完成SVST运算后求其模向量，分别记为Svs(n)和Svc(n)。

② 由式(8)求得旋变的角度向量θ(n)：

(8)

③ 因θ(n)由模向量求得，其值范围在0～90°，故需要判断θ(n)实际所处象限，以获得旋变真实的角度值。为避免Svs(n)和Svc(n)零值区域造成象限判断不准，采用最佳非零区间的象限系数法判断象限。所谓最佳非零区间是指用于象限计算的Svs(n)和Svc(n)尽量远离零值的区域。考虑两路信号变化趋势不同，在同象限区域内，当Svs(n)和Svc(n)存在交点时，由最临近交点处的ve峰值确定求解象限的采样点序号；当Svs(n)和Svc(n)不存在交点时，由Svs(n)和Svc(n)中的较小者临近最大值处的ve峰值确定采样点序号。根据该采样点序号确定的象限判断数据点记为m0、m1和m2，分别表示ve的峰值、vs和vc的峰值或谷值，然后采用式(9)计算象限系数P，根据其得到象限值s如表1所示。

(9)

式中，sign()为求符号函数。

表1 θ(n)象限判断

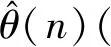
(10)

其中，Pq和Pc的计算公式为

(11)

式中,s为象限值;floor表示“向下取整”。

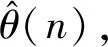
(12)

3 实验结果分析

3.1 仿真实验

为验证本文方法的有效性，用Matlab模拟旋变的三路信号ve、vs和vc，激励信号频率f=10 kHz，采样频率fs=250 kHz，ve=1 pu，变压比k=0.2。设定转速参数模拟旋变的超低速、低速、中速和高速等工况。

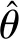
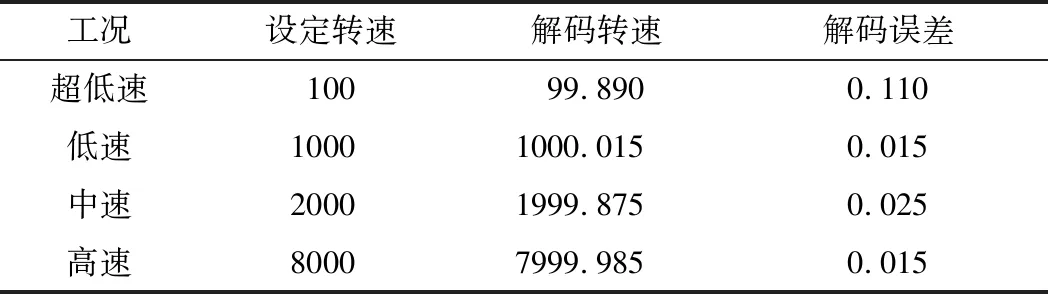
表2 SVST速度解码误差 单位：r/min

旋变工作环境复杂，输出信号会存在不同程度的噪声。为验证噪声对本文方法影响，在2000 r/min的转速工况下，对旋变信号加以噪声使其信噪比分别为40 dB、30 dB和20 dB，得到的旋变转速解码结果如表3所示，其误差最大为信噪比为20 dB时的0.525 r/min，说明基于SVST的旋变解码方法对噪声不敏感。

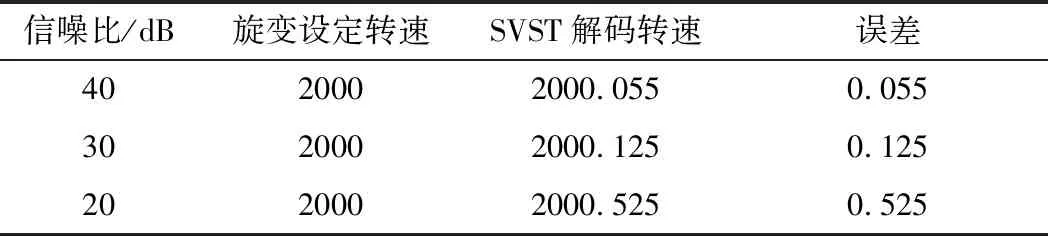
表3 SVST对含噪声信号解码结果 单位：min

3.2 实际信号实验结果

为验证本文方法对实际信号的适应性，现场采集各种工况下的旋变信号，导入Matlab采用本文方法对其进行解码运算，如图7～图10所示。图中分别为旋变在静止、超低速(100 r/min)、中速(2000 r/min)和高速(8000 r/min)工况下的SVST模向量和角度计算结果。因旋变在实际情况下有一定的噪声干扰，所以结果会伴随着噪声抖动，括号中给出的速度值为在实际实验平台中由变频器设定的转速，经本文方法解算得到各种工况下的速度值为99.9 r/min、1999.264 r/min、7999 r/min，其误差来源除算法导致外，还有电机的实际转速不一定完全达到设定值，且电机在运行过程中转速的改变需要一定的时间，SVST算法计算的时间远小于电机转速改变的缓冲时间，由结果可看出，本文算法能准确地计算出实际旋变转子的角度值和旋转速度。

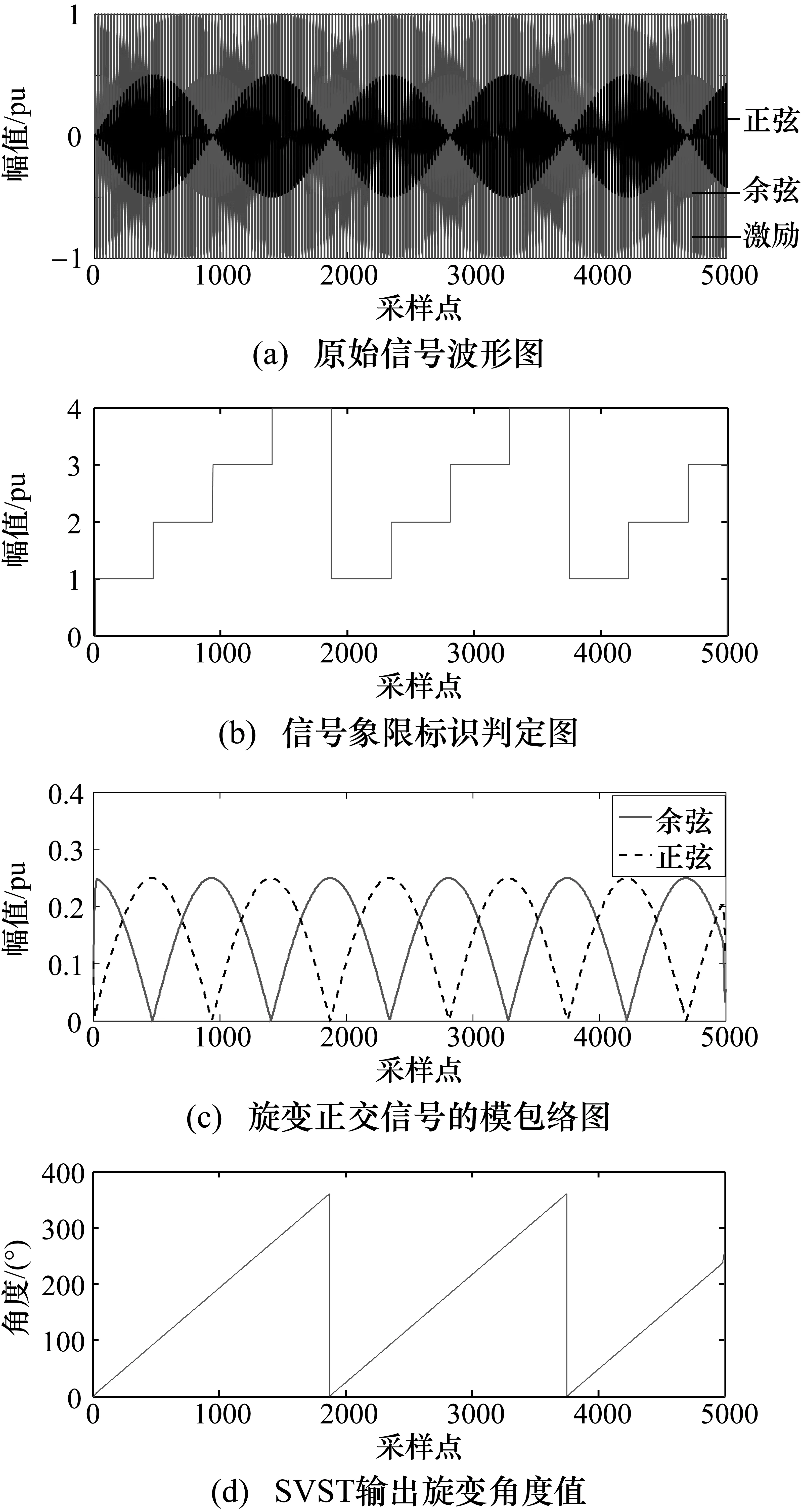
图5 旋变计算过程仿真图

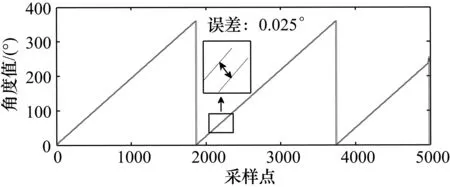
图6 测量角度结果与真实角度的比较结果

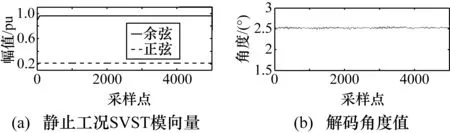
图7 实际信号静止工况解码

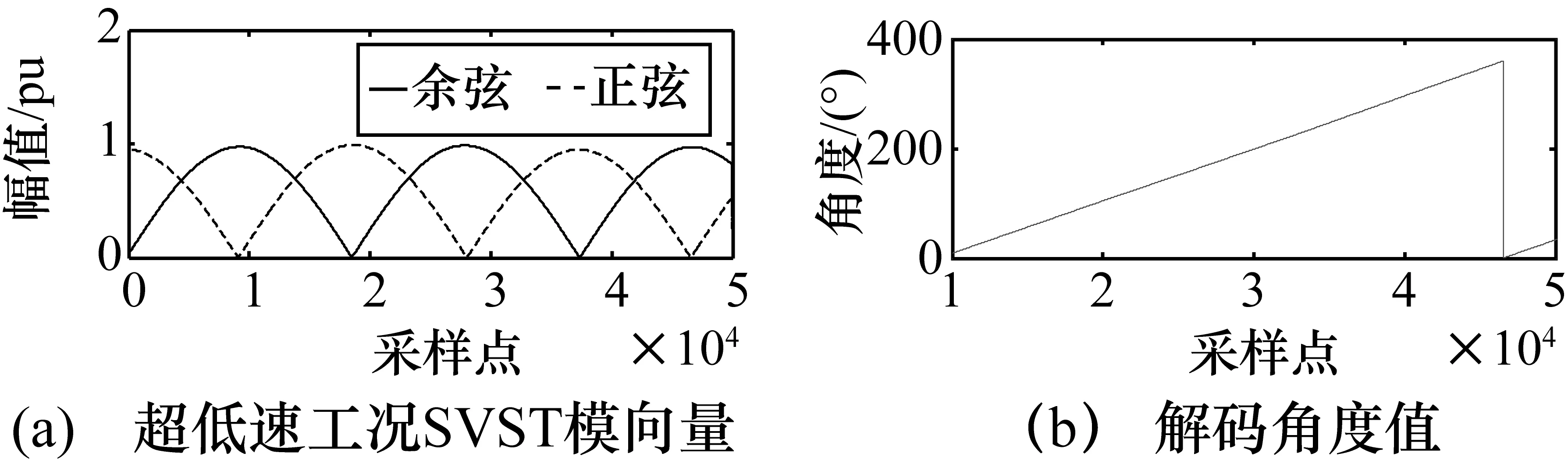
图8 实际信号超低速工况解码

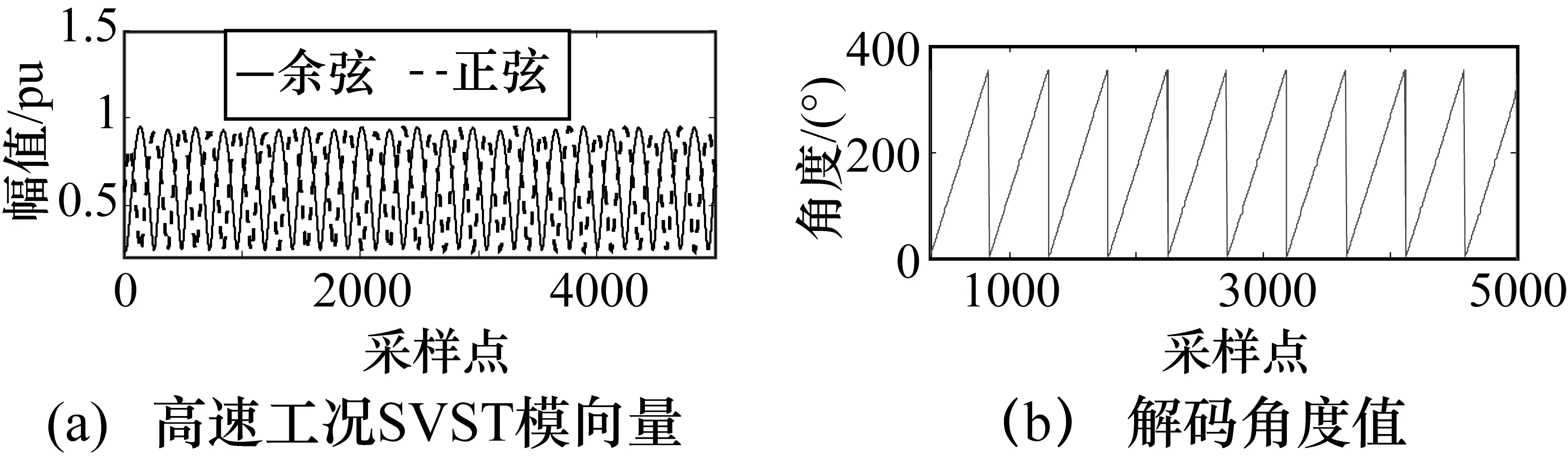
图10 实际信号高速工况解码

3.3 运算效率比较

为验证单向量S变换方法较S变换在运算效率方面的优势，测试不同的数据点下SVST和ST的运算时间，结果如表4所示，由表中可看出，随着数据量的增加，S变换的运算时间呈指数增长，数据量为6000时，计算时间达到5058 ms，因此，S变换的实时性很差；随着数据量的增加，SVST的运算时间也会增加，但当数据达到5000时，SVST的运算时间只是S变换的1‰，所以，本算法作为一种检测旋变信号角度的时频分析方法，具有一定的研究意义。

表4 SVST和S变换运算时间对比 单位：ms

4 结束语

本文利用SVST提出一种新的旋变角度和转速解算方法，采用仅IST的一维向量，填补了时频分析方法应用与旋变解码的空白。由SVST提取的模包络对噪声不敏感，能够适应不同工况下的精确解码需求。仿真和实际信号实验结果表明，本文方法解码的速度绝对误差小于0.6 r/min。在对角度解码精度要求不是很高的系统中，该方法完全可行。本文方法可以方便地集成在DSP系统中，无需专用解码芯片，是一种低成本的旋变解码方案。