大规模轨迹数据并行化地图匹配算法

康 军,2， 郭佳豪， 段宗涛,2， 唐 蕾， 张 凡

(1.长安大学 信息工程学院，陕西 西安 710064； 2.陕西省道路交通智能检测与装备工程技术研究中心，陕西 西安 710064)

城市计算是一种利用大数据技术解决城市治理问题的新兴领域，而轨迹数据是城市计算应用中最重要的数据源之一[1-2]。随着相关问题的产生，以及计算性能的极大提升，对大规模轨迹数据的研究非常广泛。如文献[3]，第一次利用轨迹数据进行实验，分析出出租车司机普遍存在拒载现象，并且根据算法估计出北京市高收入出租车司机的拒载概率大约为8.25%。滴滴[4]每天有数百万司机为上亿用户提供打车服务，针对订单的分配问题就需要准确、实时的司机与乘客的位置信息。

为了更好地利用大规模轨迹数据，车辆导航定位等技术非常重要，而地图匹配正是车辆导航技术中的核心技术之一。目前对于地图匹配算法的研究非常广泛，如文献[5]提出一种加权几何地图匹配算法，该方法利用水平精度因子、行驶速度、行进距离来获取动态加权系数，利用加权系数与几何特征值的乘积来选取匹配道路。文献[6]和文献[7]是两种基于隐马尔可夫模型的高级地图匹配算法，这种方法主要针对路网复杂，轨迹采样频率低等复杂场景下的地图匹配。现有的研究主要针对地图匹配的精度问题，而数据规模的增大，使得传统的串行算法不再适用。文献[8]提出了一种基于Hadoop的分布式地图匹配算法，但实验的最大数据量为20万个轨迹点，数据规模并不是很大。针对此问题，提出一种基于大规模轨迹数据的并行化地图匹配算法，并利用基于GeoHash编码的网格化地图对候选道路的选取进行了优化。实验使用了大规模出租车轨迹数据，对比了该算法与文献[8]的算法对同规模轨迹数据的运行时间，并参考文献[9]采用的3种并行计算的性能比较方式对本算法进行测试。

1 问题分析

1.1 串行地图匹配算法

地图匹配算法主要有基于几何的地图匹配算法、基于拓扑的地图匹配算法、高级地图匹配算法等。在众多的地图匹配算法中，选取一种动态加权的地图匹配算法[10]进行并行化实现。该算法准确率达到96.7%，并且算法的各个特征以及权值系数计算过程非常简单、易于实现，非常适合用于解决轨迹数据规模大的地图匹配问题。

该算法的主要步骤是取候选道路，计算待匹配点与候选道路的投影距离、航向夹角、轨迹夹角这3个特征值，再分别计算每个特征的权值系数，最后加权求和，选取得分最小的道路作为候选道路，待匹配点在该道路上的投影点为修正后的轨迹点。得分的计算公式如下：

(1)

式中,di为投影距离;Δθheadi为航向夹角；Δθtraji为轨迹夹角;Wi为投影距离的动态系数;Whead为航向夹角的动态系数;Wtraji为轨迹夹角的动态系数;N为候选路段个数。

1.2 网格化地图

在地图匹配过程中首先要选取候选路段，然后在候选路段中根据不同的匹配算法选取最为匹配的路段。文献[10]中选取经纬度的L∞距离作为选取的距离度量，这种方法得到的范围比欧式距离、曼哈顿距离得到的面积大，可以最大限度地选取候选路段。而此方法需要遍历整个路网，由于真实路网的数据量很大，因此这种方法非常消耗时间。候选路段的选取问题可以抽象为一种空间索引问题。如文献[11]采用了二级网格索引，可以将候选路段的搜索进行优化，但该方法需要将地图数据划分为两个刻度不同的地图数据，索引具体的网格也需要两次完成。GeoHash[12]是一种有效的地理编码方式，可以将经纬度利用二分法进行二进制编码，再用Base32编码进行压缩。GeoHash将二维的经纬度坐标转换为一维的字符串编号,每个编码代表一个矩形区域，编码的长度决定矩形区域的大小，这种编码方式非常适合网格化地图问题。

原始的西安市地图是一个左下角坐标为(108.67,33.7)、右上角坐标为(109.81,34.75)的矩形区域。将经纬度分别按18位、17位进行GeoHash编码，如表1所示，此时的经纬度误差均为0.00136，可以将所有路网分割为边长为0.00136°的矩形区域。这样可以把这个区域分割为大约840×774个网格。每个网格是一个经度边长为0.00136°、纬度边长为0.00136°的矩形区域，且每个网格刚好可以用一个GeoHash编码的字符串表示。

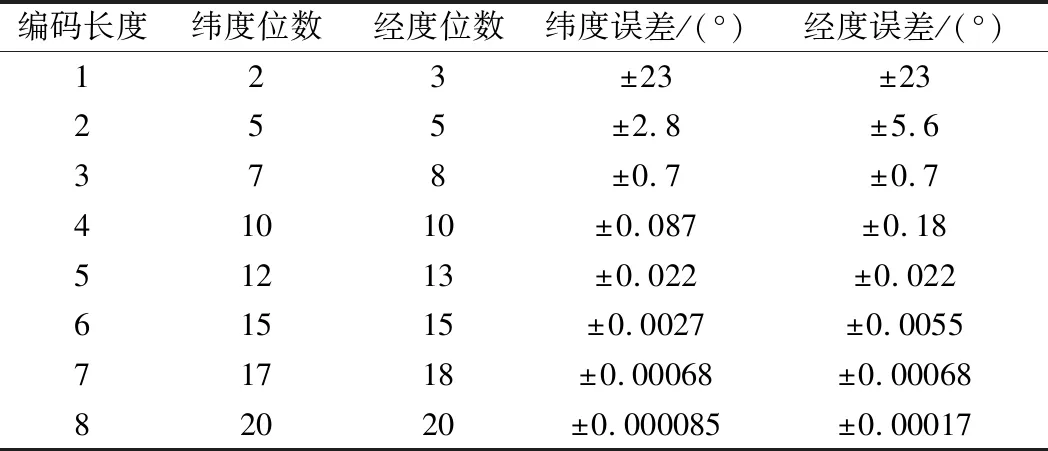
表1 GeoHash编码精度表

网格编码过程如下。

① 根据对角线上两个坐标求平均值，可以得到网格中心点的坐标；

② 利用二分法将中心点的坐标转为二进制码；

③ 将经度放在奇数位，纬度在偶数位，这样可将两个二进制码合并成一个二进制码；

④ 最后进行Base32编码，得到最终的网格编号。

如图1所示，点C为中间网格的中心点，点C对应的编码即为该网格的编码，周围的道路为Path1、Path2，其余的点为道路上的结点。

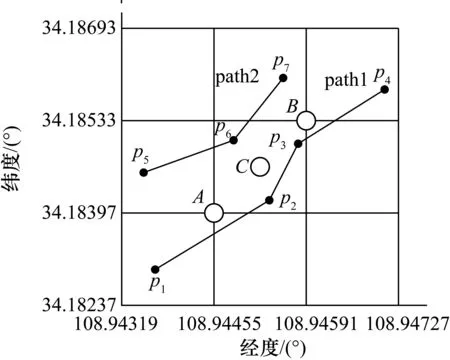
图1 网格化地图示意图

1.3 轨迹数据预处理

原始轨迹数据主要包含车牌号、时间戳、经度、纬度、速度、航向夹角和车辆状态等字段。实验使用的数据为西安市出租车轨迹数据，采样间隔为30 s，每辆车每天产生大约2880条轨迹数据。所有出租车每天大约产生2 GB左右的轨迹数据，最大实验数据约为14.7 GB。

首先需要对数据进行数据清洗，原始的轨迹数据是无序、且含有异常数据的。数据清洗包括以下几步：数据去重；去除汉字；去除异常轨迹点；按车牌、时间排序。

在式(1)中参数Δθtraji为航向夹角特征，在数据清洗过程中，需要利用连续两个轨迹点的轨迹距离判断是否为异常点，这时可以直接计算出轨迹夹角，减小后续匹配的计算量。

在计算轨迹夹角之后，对每个轨迹点计算其对应的GeoHash编码，这个编码就是该轨迹点所对应的地图网格的编号，这样可以增强轨迹数据的内聚性。编码方式与网格化地图的编码方式一致。如轨迹点坐标为(108.945652,34.184875)，编码为wg27cbu，将该编码也保留在原始数据中。

1.4 选取候选路段

当匹配一个待匹配点时，先用GoeHash编码计算该点在地图中的网格编号，根据网格编号可以查找该网格的路段数据，以及周围的8个网格的路段数据，字典型的查询时间复杂度为O(1)。在进行候选路段选取时，选择待匹配点周围9个网格中的数据进行遍历。这样就把地图数据规模缩小至原始地图面积的0.00138%，极大地降低了时间复杂度。如图2所示，小圆圈表示待匹配点，字符串分别表示9个网格的网格编号，虚线的网格为最终的候选路段范围。

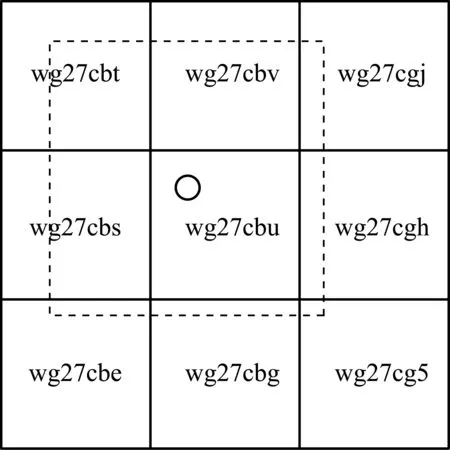
图2 候选道路的选取

2 并行化地图匹配算法

2.1 Spark介绍

随着科技的发展，位置信息很容易被记录下来，大规模的轨迹数据是城市计算的重要数据来源之一。而Spark等开源的大数据平台的出现，使大规模数据的计算更加便捷。将动态加权的地图匹配串行算法改为Spark RDD的编程模型，可以快速地完成大规模地图数据的地图匹配任务，为城市计算等应用提供了有力的保证。

2.2 分区方法

为了使并行计算更为有效，将网格化的地图数据与带有网格编号的轨迹数据利用HashPartitioner的方式进行分区。设轨迹点A的GeoHash编码为grid，grid的数据类型为字串类型，则轨迹点A利用Spark的HashPartitioner分区器进行分区时，其分区编号key可表示为

key=String.hashcode(grid) modn

(2)

其中，String.hashcode()为字串类的hashcode函数；mod表示整数求余运算；n表示设定的分区数目。将网格地图数据分配给各个分区时，首先使用如式(2)所示的方法计算各个网格所对应的分区编号；然后根据1.4节的候选路段选取办法，确定当前网格的其他8个相邻网格；最后将上述9个网格对应的网格-路段数据分发给选定分区。

2.3 算法介绍

如表2所示，并行化地图匹配算法的输入为地图数据、预处理后的轨迹数据、分区数，输出为匹配后的轨迹数据。

表2 并行化地图匹配算法

首先将原始的地图数据映射为网格编号为key的网格化地图数据，再得到轨迹点的网格编号。然后分别对地图数据和轨迹数据进行分区，将相同key的轨迹数据和地图数据进行连接，得到该轨迹点对应的候选路段数据。并行计算每个点对应的每条候选道路的投影距离特征、航向夹角特征、轨迹夹角特征。计算最终得分，并对候选路段按得分进行升序排列，取出得分最低的候选路段作为最终的匹配路段。最后对数据进行重新合并，返回匹配后的轨迹数据。

3 实验与分析

3.1 实验数据及环境

实验数据来源于西安市交通管理部门，为出租车1周产生的轨迹数据，数据量约2亿条。轨迹数据的格式以及清洗过程如1.3节所示。电子地图数据为西安市地图数据，包含2.9万条西安市城区道路。

实验使用的Spark集群包含13个Worker节点，252个Core，每个节点32 GB内存，总内存416 GB。原始数据存储在HDFS平台上，运行的结果再保存到HDFS上。Spark的部署模式为Standalone模式，该模式具有容错性，且支持分布式部署等优点，适用于真实场景下大规模数据的计算。

3.2 算法效率对比

在相同数据规模下，使用本方法与文献[8]中的实验结果进行对比，如表3所示。显然新的方法在性能方面取得了很大的提升，特别是当数据量增大为20万条时，新算法的运行时间为旧算法的44%，比数据量小时性能提升的效果更好。原始方法并没有在足够大的规模下进行试验，将数据上升至接近3000万条，新的算法仍然高效。提升至2亿余条，仍然可以在短时间内完成匹配，最大数据规模是原始算法最大规模数据(20万条)的1000倍以上，时间开销仅用了其32倍。新的算法更加适合于大规模轨迹数据的地图匹配问题。

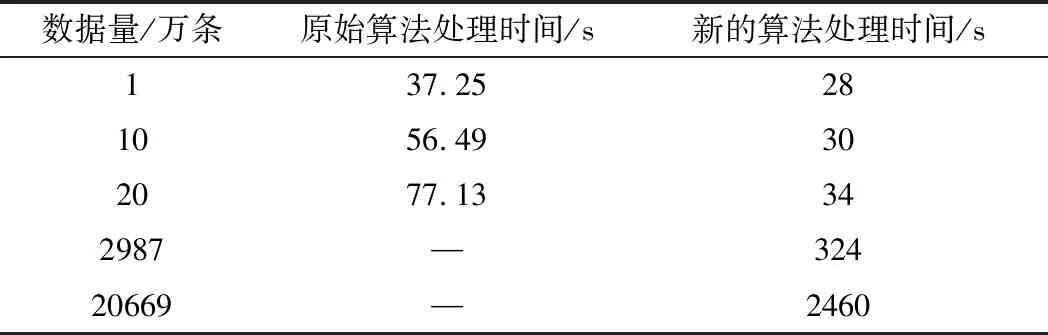
表3 新算法与原算法效率对比

3.3 并行度优化

在并行计算中，并行度对计算的效率有很大的影响，而Spark中分区数的选取决定并行度的大小。如果分区数过小，有的节点没有分配到数据，会造成资源浪费。如果分区数目太大，计算过程中各分区之间的Shuffle很大，也会降低计算的效率。分区数由100到1000(步长为100)，分别对同一天的轨迹数据进行地图匹配，数据量大约为3000万个轨迹点，占内存2 GB左右，实验的运行时间测试结果如图3所示。图中横轴代表分区数，纵轴代表运行时间。由图中可以看到，当分区数为500时运行时间最短，运行时间为5.4 min，比最差的情况少用了38%的时间。由此可以看出分区的选取对于并行计算的效率影响很大，而不同数据规模最优分区数不同，在进行并行计算时可根据规模大小对分区数目做一些适当调整。

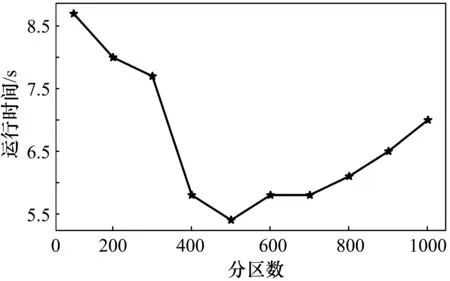
图3 不同分区数的运行时间

3.4 规模增长性测试

随着数据规模的增大，各个节点的负载会变大，而且节点之间的通信量也会变大，这时算法的性能会有所下降。因此，引入规模增长性这一指标，对规模增长引发的并行性能变化情况进行测试，如式(3)所示。

Sizeup(n)=Tn/T1

(3)

式中，T1为一天的数据量所需匹配时间；Tn为n天的数据所需匹配时间。

将1～7天规模的数据量分别测试运行时间，根据式(3)进行计算规模增长性，结果如图4所示。显然，随着数据规模成倍的扩大，规模增长性接近线性增长，并行算法性能上并没有太大的下降，稳定性比较高。

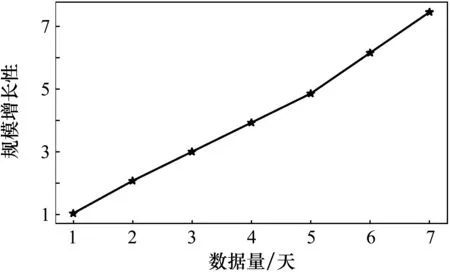
图4 不同规模数据的运行时间

3.5 加速比测试

在并行计算中，加速比这一指标表示随着节点数的增大，并行计算相对串行计算性能上的提高，如式(4)所示。

Speedup(p)=T1/Tp

(4)

式中，Speedup(p)为加速比；T1为单处理器下的运行时间；Tp为P台处理器的运行时间。对不同节点数下，测试同一天轨迹数据的匹配时间。测试结果如图5所示，横轴代表使用节点数，左纵轴代表运行时间，右纵轴代表加速比。随着节点的增加，运行时间下降，但下降的趋势变慢；加速比在上升，但上升的趋势趋于缓慢。这是由于节点数增加，节点之间的通信开销增大。

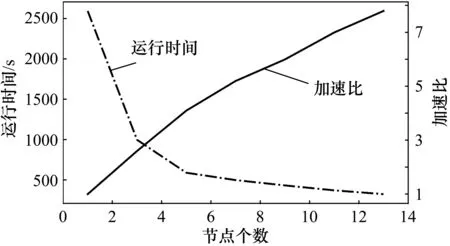
图5 加速比测试

3.6 可扩展性测试

可扩展性由加速比产生，代表着算法性能随着节点的增大而提高的能力，如式(5)所示。

Scaleup(p)=Speedup(p)/p

(5)

式中，Scaleup(p)为可扩展性；Scaleup(p)/p为节点数等于p时的加速比与节点数p的比值。测试结果如图6所示。可见，随着节点的增加，可扩展性在缓慢降低。

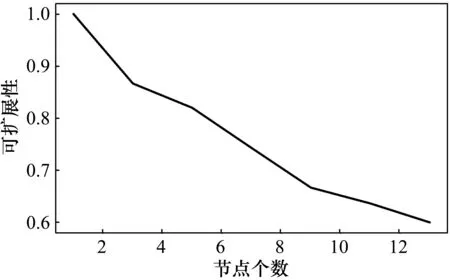
图6 可扩展性测试

4 结束语

提出了一种基于大规模轨迹数据的并行化地图匹配算法。在候选道路的选取中采用了一种基于GeoHash编码的网格化地图方法，将候选道路查询的时间复杂度下降了一个量级。采用Spark平台，实现了一种并行化的动态加权地图匹配算法。经试验测试，该算法可以短时间内完成大规模数据的地图匹配任务，且稳定性高，具有良好的可扩展性。在很多真实应用场景下，地图匹配需要具有实时性。因此，下一步的研究应该将批处理方式改进为流处理，使该算法得到更加广泛的应用。