改进小波算法在光纤温度传感器中的应用

(北京工业大学 信息学部，北京 100124)

温度，对于工业控制来说，是一个至关重要的参数。传统的温度传感器是依赖于电学，例如热电阻、热电偶，这类传感器不仅是一种“点”式的感应方式[1]，而且受限于高温、高辐射和电磁干扰环境。1983年英国的Hartog通过液体光纤中的拉曼散射效应实验了分布式光纤温度传感，为石英光纤分布式温度传感奠定了基础[2]，用光纤进行温度传感，不仅具有可测点广、温度信息量大和传输距离长等优势，而且可以摆脱电磁干扰，耐高压、抗腐蚀，是一种快速多点测量并精确定位的高性能温度传感方式。光纤既作为传感物质又作为传输数据介质，大大减少了成本，提高了利用率。因此，光纤测温广泛应用于煤矿[3-4]、电力[5-8]、石油[9-11]和航天[12-13]等各个领域。

目前，光纤测温技术主要是FBG(光纤布拉格光栅)与拉曼散射光纤测温[14-16]。其中光纤布拉格光栅测温是采用一根光纤上连续刻入多个布拉格光栅，利用复用技术实现的准分布式测量。这种方式不仅成本高，并且设计复杂，存在低灵敏度和交叉敏感问题。与之相比，拉曼散射光纤测温不受光源波动、光纤成分和应力等影响，对测温点位置测量精确，寿命长，成本低。该方法存在散射过程中信号弱，且信号中噪声的干扰不可忽略的问题。针对此问题，国内外学者提出了许多解决方法，如王剑锋[17]等人在硬件上添加一路激光器来减小温度误差，这势必造成成本的增加；孙柏宁[18]采用累加平均法进行降噪，但其测量时间增长，不适合快速变化的温度场；沈小青[19]等人采用小波变换直接高频信号置零方式，但易存在信号丢失严重问题；江虹[20]等人构造阈值函数法，张正文[21]、付勇[22]采用阈值法进行滤波，但阈值的选择不具有系统的普适性；王慧[23]等人采用LMS算法，势必造成算法空间复杂度增加。

由于小波模极大值滤波算法具有分析非平稳信号能力，已被广泛应用于众多领域。笔者则是在前人的基础上提出了一种改进的小波滤波算法，采用基于窗口小波的相关性模极大值算法并结合尺度自适应方法进行信号滤波处理，以提高测温精度，增加信噪比。

1 传统小波模极大值滤波原理与算法

分布式光纤拉曼温度传感系统中拉曼散射信号比较微弱，来自环境、系统器件等的噪声不可忽视，由于系统的信噪比比较低，为了解调出精确的温度值，必须对采集信号进行处理。

考虑到小波具有多分辨率分析的特性[24]，滤波效果明显，采取以模极大值小波滤波方法作为基础的方法，其主要原理是如下。

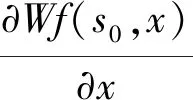
通过上述定义，可以看出小波变换模极大值点在点x0的左右邻域都是严格局部最大的[25]。

信号与噪声的Lipschitz指数[26]：

设f(x)∈L2(R)，若f(x)对∀x∈δx0，小波ψ(x0)连续可微，并具有n阶消失矩(n为正整数)有

|Wf(a,x)|≤kaα

(1)

其中k为常数，则称α为x0的奇异性指数，从式(1)可以看出，当尺度a趋于0时，

|Wf(a,x)|≤O(aα)

(2)

奇异点与其余普通点相比，其奇异指数小于其邻域内普通点的奇异指数。因此假设x0为奇异点，当a充分趋于零时，x0的小波系数衰减得最慢。因此在x0的邻域δx内的点收敛于x0，并且成为了小波模极大值。a一般取为2j，则

log2|W2jf(x)|≤log2k+jα

(3)

若f(x)的Lipschitz指数α>0，该函数的小波变换模极大值与尺度j是正比关系；反之，若指数α<0，则模极大值与尺度j成反比。若α=0，则模极大值不发生改变。通过此特性区分出噪声与信号，常用信号的指数一般是大于0的，即使信号是不连续的奇异点，只要在某一邻域内有界，则α=0。然而噪声所对应的Lipschitz指数是小于0的。

基于上述原理，将采集的信号进行小波分解变换，保留随分解尺度逐渐变大的模极大值系数，最后进行信号的重构，从而达到滤除噪声、改善温度测量误差的效果，上述算法流程如图1所示。

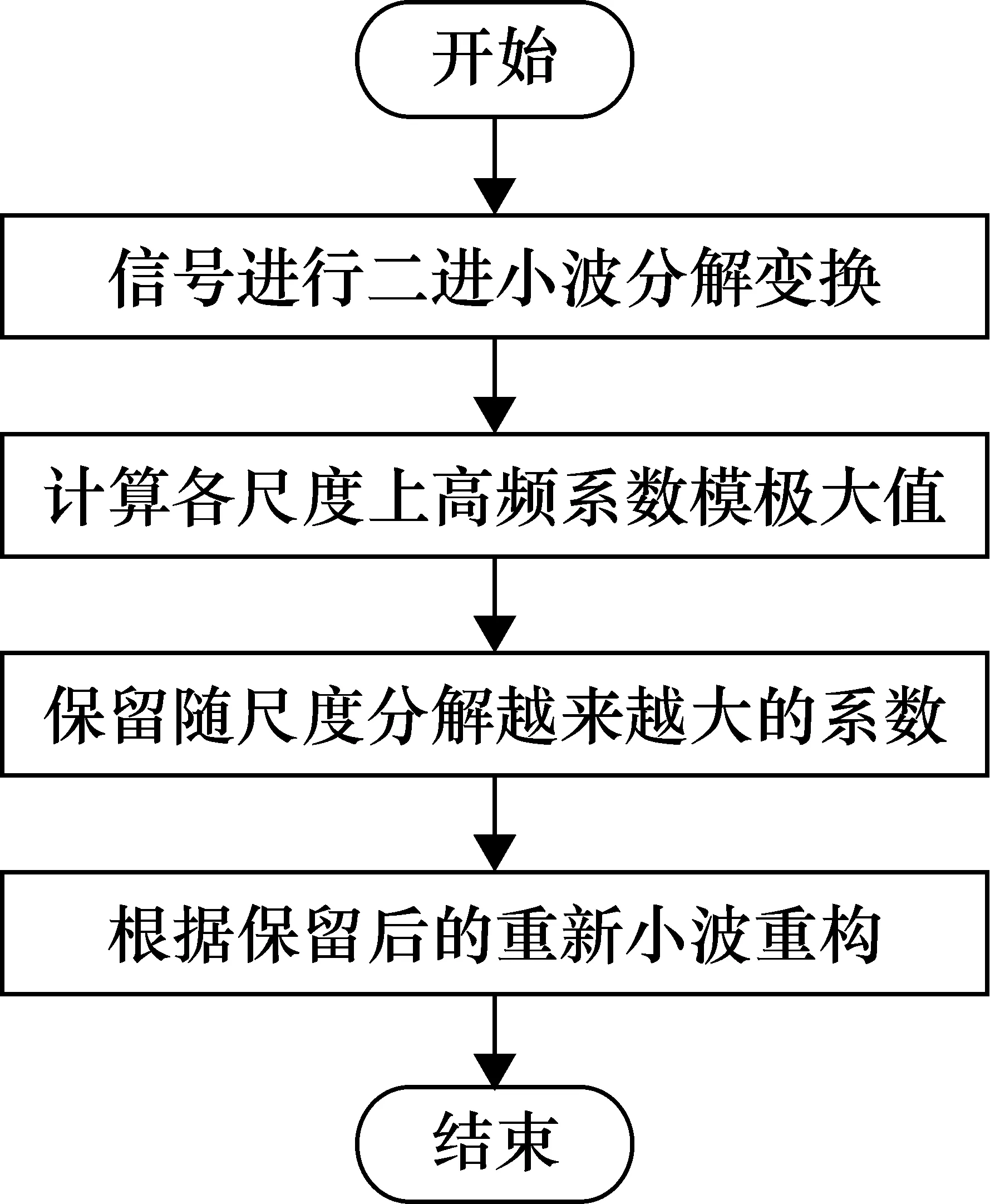
图1 模极大值小波信号处理流程图

2 改进的小波算法

传统的模极大值算法，分解尺度越大，含信号的小波系数越多，含噪声的小波系数越来越少。但是，由于信号进行分解时会造成小波系数的偏移，大尺度有效信号和小尺度的有效信号出现偏移。因此，一旦取错一个大尺度下的模极大值，若直接以取错了的大尺度系数去寻找小尺度的小波系数，偏移了的小尺度小波系数中，很可能就会出现满足式(3)的系数，即满足了随分解尺度变大的小波系数。但是这里取出来的大、小尺度小波系数都是错误的，以取错了的系数进行重构信号势必存在误差。为在大尺度上取出的小波系数中包含绝对信号，引入信号相关性特性来提高噪声与信号的捕捉能力。由于大尺度上携带的信号小波系数占比多，其中信号相关、噪声之间则不具有此相关性。考虑在最高尺度j的小波系数ψj,k两边加上幅度为1、宽度为2n的矩形窗口，则此窗口内的小波系数和为

(4)

j尺度上Sj,k的相关系数和归一化相关系数分别为

Rj,k=Sj,k×Sj-1,k

(5)

(6)

其中，

(7)

(8)

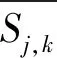
加入信号相关性的算法应用于实际测试发现，该算法捕捉信号与噪声能力明显提升，但温度剧增时由于分解尺度的影响，分解太大重构后会使得信号丢失，现象见图2矩形框标记区域；而如果采用小尺度，在温度变化不剧烈时，会导致噪声滤除不净(见图3)。因此，考虑根据信号的变化剧烈程度自适应地来选取尺度大小。图2与图3中曲线①是信号曲线，曲线②分别是使用4尺度与使用3尺度进行信号分解滤波。

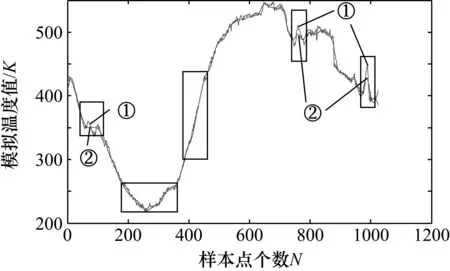
图2 高尺度突变地方出现信号丢失

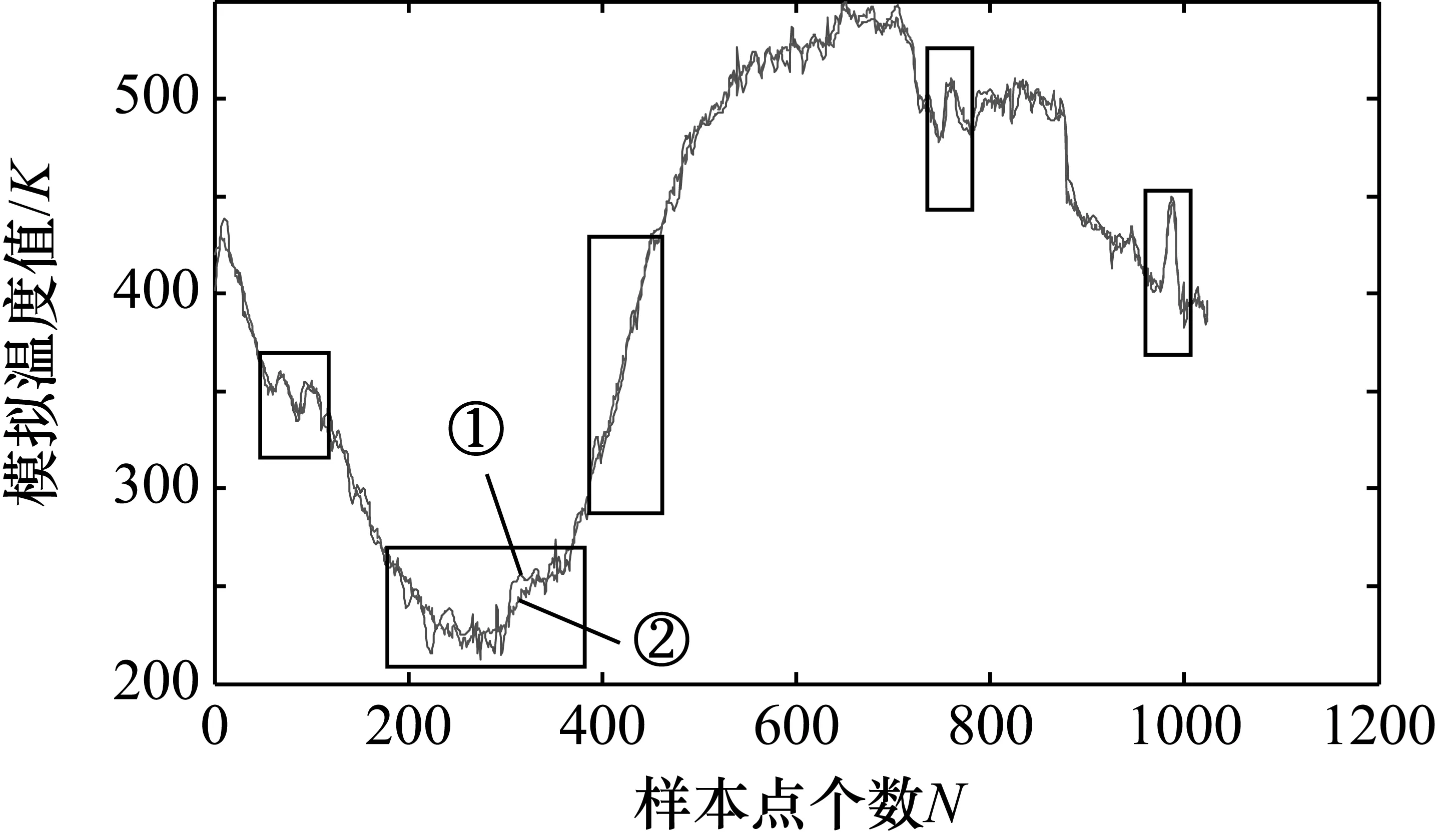
图3 低尺度平滑地方噪声未滤净

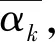
3 实验分析

为了对比小波模极大值算法、窗口相关性模极大值算法、窗口自适应分解尺度相关性模极大值算法这3种算法对信号的滤波效果。在Matlab中模拟温度数据，首先生成1024个数据，如图5所示，随后添加不同信噪比的噪声信号，图6为添加-40 dB噪声与信号叠加后的波形图，分别使用3种算法进行滤波。

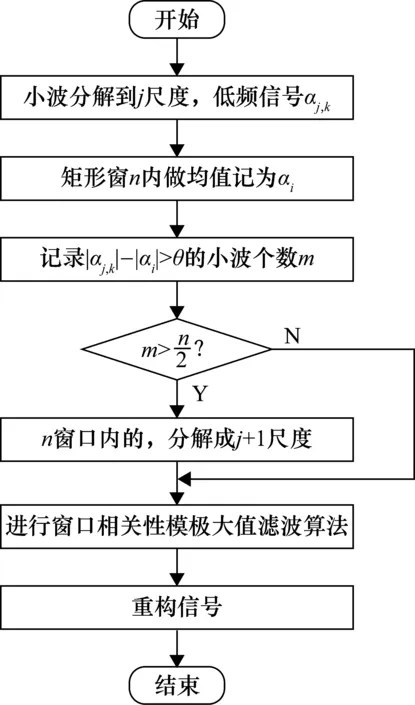
图4 自适应分解尺度算法流程图

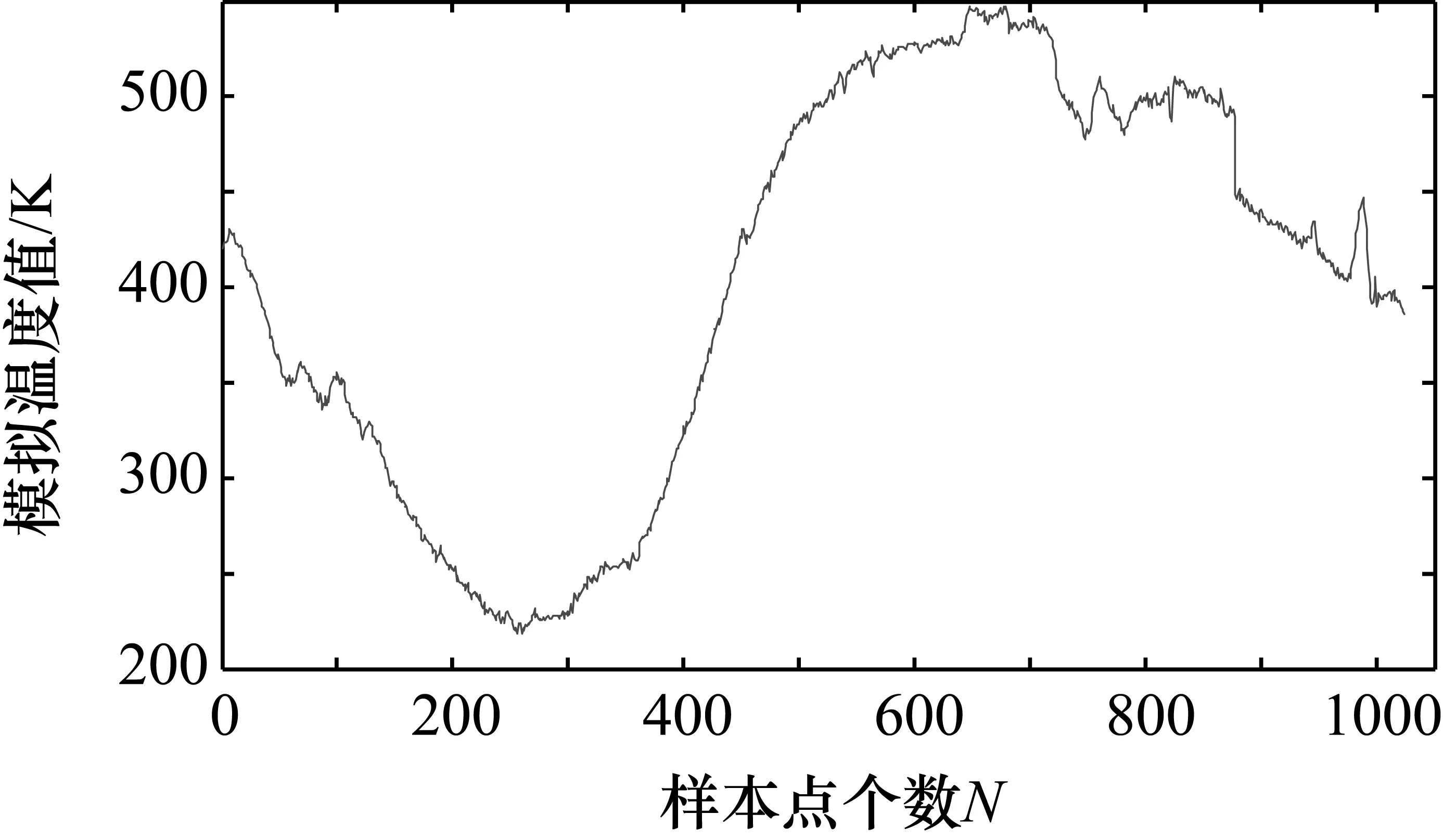
图5 未加噪声的信号波形

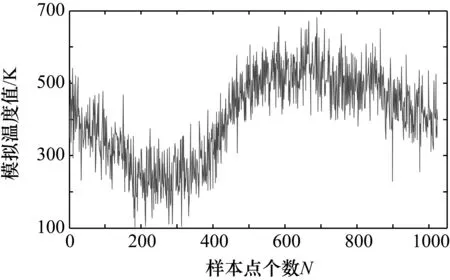
图6 添加噪声后的波形(-40dB)

为了观测滤波后的信号与原始期望信号之间的误差，以原始期望信号与滤波后信号的误差均方根作为判定标准：

(9)

式中，d(n)为滤波后信号；q(n)为未加噪声的原始信号；N为采样点个数；σ为误差均方根。通过550组试验，统计比较结果，不同信噪比下的滤波效果对比如表1所示。

由表1可知，当添加噪声的信噪比比较大时，3种算法的滤波效果都不错；当添加噪声的信噪比降低时，前两种算法的性能明显下降，而窗口自适应分解尺度相关性模极大值算法仍然有很好的滤波效果。从图7、图8和表1都可以看出，当添加信噪比为-30 dB噪声时，前两种已经无法滤除正确的噪声。图9与表1可以看出信噪比降为-40 dB时，改进的方法仍然能获得较满意的效果。

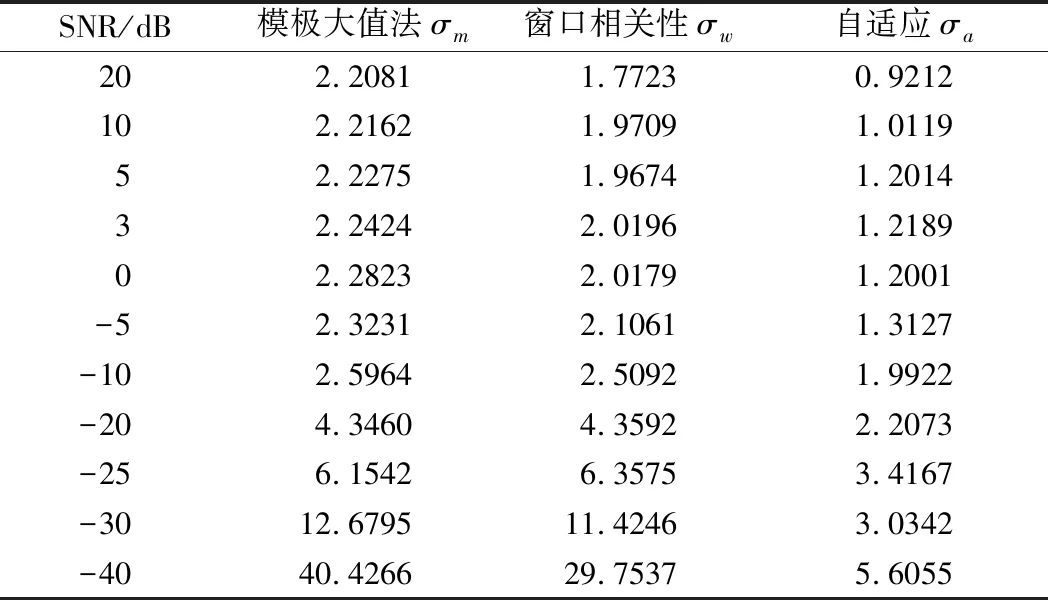
表1 不同信噪比3种算法滤波效果

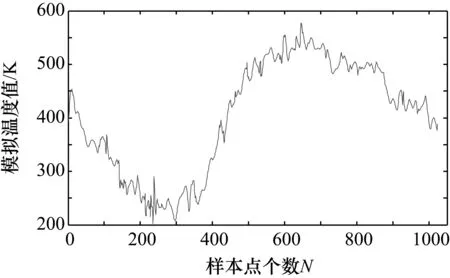
图7 小波模极大值算法(-30dB)

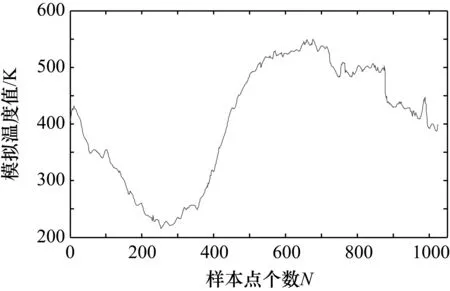
图8 窗口相关性模极大值算法(-30dB)

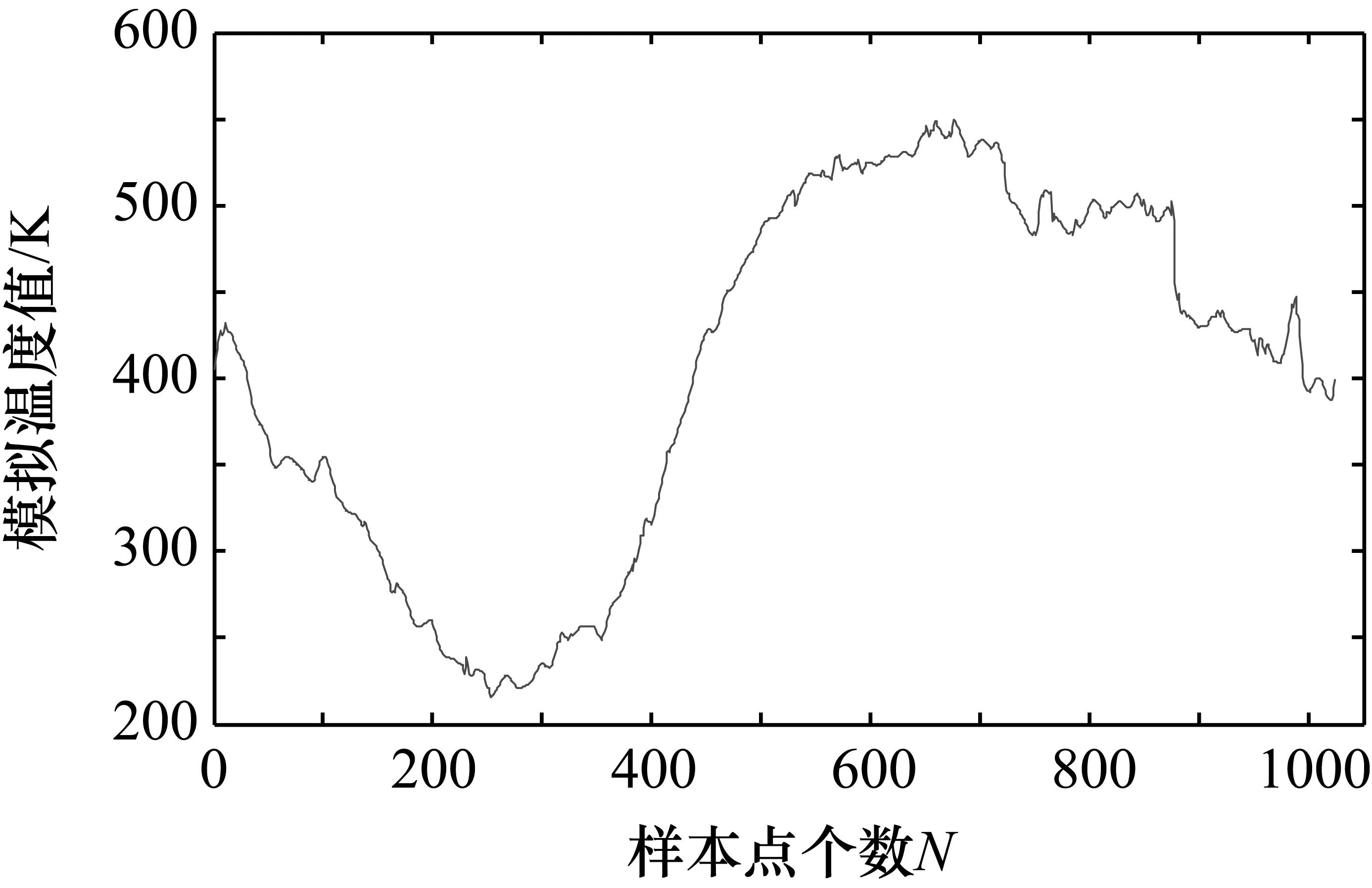
图9 自适应分解尺度相关性模极大值算法(-40dB)

针对上述分析，将窗口自适应分解尺度相关性模极大值算法移植运用到图10所示的光纤温度系统。

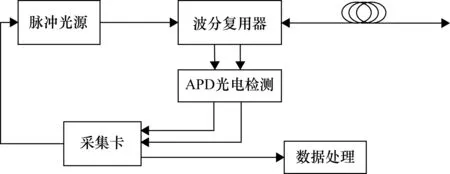
图10 系统结构示意图

脉冲光源主要是用DFB(分布式反馈)1550 nm半导体激光器、驱动电路、温控电路和数据传送电路组成，发射波长1550 nm脉冲光源，通过波分复用器传送到连接的多模光纤(62.5/125 μm)，当传感光纤的温度变化时，传送回波分复用器的Stokes光和Anti-stokes光进入InGaAs-APD(铟砷化镓-雪崩光电二极管)的光电转换电路，再传送到高速采集卡，高速采集卡经过累加处理，通过数据传送电路输出给上位机，上位机做算法处理数据，同时上位机软件可向采集卡发送数据同步控制脉冲光源发送光波。

实验时，将传感光纤置入设定好的恒温仓中，改变恒温仓的温度值，每个温度值进行20组实验，最终统计数据见表2，T为恒温仓温度，T1为未使用算法时温度值，T2为使用算法后的温度值，ΔT1为使用算法前温度值与实测温度值误差，ΔT2为使用算法后温度值与实测温度值误差。图11为光纤在室温28 ℃的情况下，置传感光纤23 m处的10 m光纤于恒温仓内，恒温仓设置75 ℃的光纤整体温度分布截图，图框区域为放大后的截图。图12为光纤在室温25 ℃下，置传感光纤2550 m处的10 m光纤于恒温仓内，恒温仓设置16 ℃的光纤整体温度分布截图，图框区域为放大后的截图。

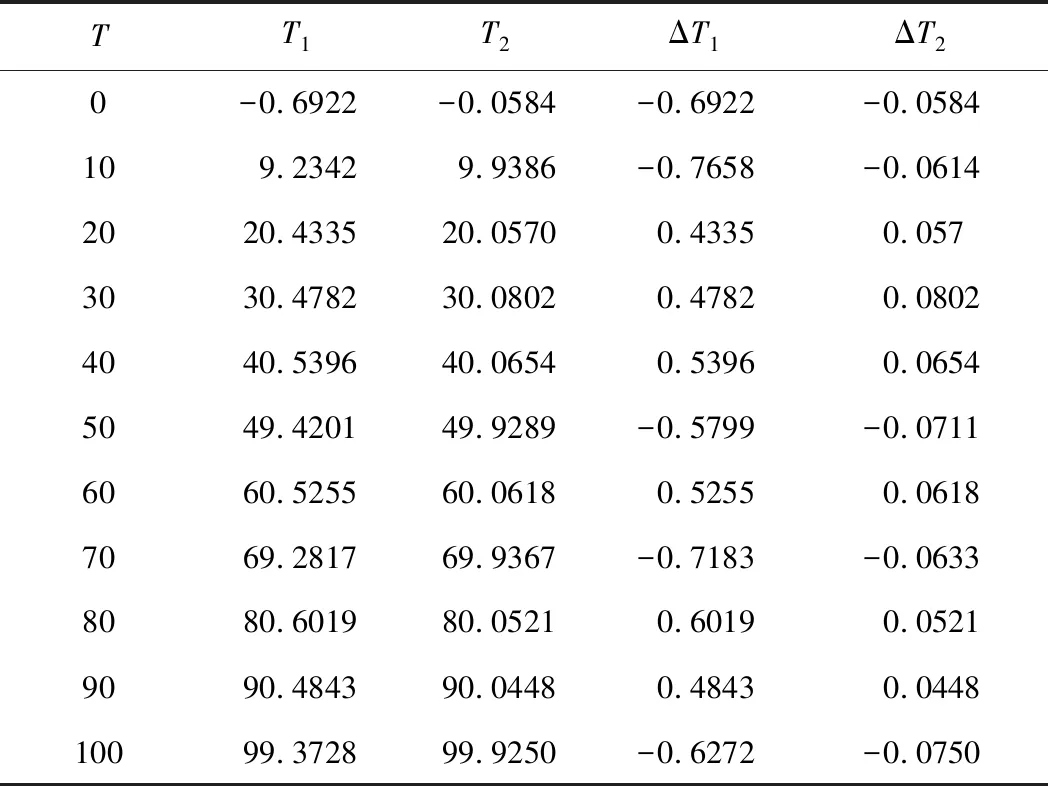
表2 不同温度值算法前后对比图 单位：℃

通过表2、图11以及图12都可以观测到，不同温度下，使用算法后的精确度都有很好的提升。通过表1的11个温度值共220组温度数据统计，温度误差平均缩小了0.5233 ℃，性能明显提高。

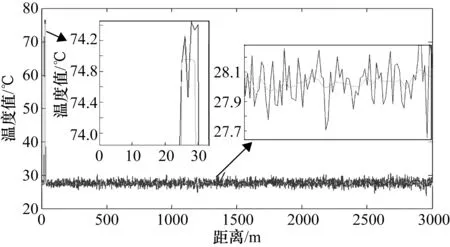
图11 光纤温度分布图(室温28℃恒温仓75℃)

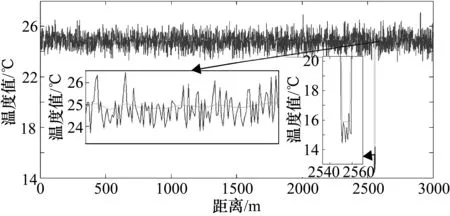
图12 光纤温度分布图(室温25℃恒温仓16℃)

4 结束语

本文针对分布式光纤温度传感器系统中，基于传统模极大值小波滤波原理，提出了窗口自适应分解尺度相关性模极大值算法，其主要特点有：利用最大尺度上的信号相关性，提高了噪声与信号的捕捉能力；结合自适应分解尺度，解决尺度小时，噪声滤除不干净，尺度大时，信号丢失问题。本文模拟仿真了温度数据，添加不同信噪比的噪声，证明了与以往同类算法相比较，改进后的算法有很好的效果。最后，将算法移植到测温系统中，再次验证了此算法对温度的精度提高效果明显。