二项分布下基于鞍点逼近的总体成数置信区间的构造
夏丽丽,田茂再,朱 钰
(1.北京工业大学 应用数理学院,北京 100872;2.中国人民大学 a.应用统计科学研究中心;b.统计学院,北京 100872;3.西安财经大学 统计学院,陕西 西安 710100)
一、引 言
当今社会发展迅速,人们的生活也越来越富裕,卫生保健意识也在不断增强,因此就医的人数就大大增加,这也就增加了医疗事故的发生率。虽然政府已经出台了很多相关法律政策来制约医疗事故的发生,但医疗事故的发生率呈现上升的趋势,特别是一些医疗机构,出于商业目的盲目追求效益而造成的医疗纠纷必须要重视。通过对医疗机构医疗事故的发生率进行研究,可以让更多的人认识到问题的严重性,加强监管力度,从而找到医疗事故发生率比较低的医疗机构进行就医,希望一些医院能够认识到问题的严重性,从源头上进行治理,因此对医疗事故发生率的区间估计尤为重要。通过分析发现,医疗事故的发生率和统计学中的成数非常相似,这就让我们有了一个新的角度对医疗事故的发生率进行估计。可是对医疗事故发生率进行点估计不够精确和可靠,经常用区间估计来弥补点估计的不足,这样一来,问题就变成了从研究总体成数的置信区间入手研究医疗事故发生率的置信区间。
抽样调查研究的基本问题之一就是对总体成数进行区间估计,因此选择较好的区间估计方法显得尤为重要。曲卫彬在1993年阐述了总体成数估计中两个不容忽视的问题,既要明确总体成数的含义,又要弄明白成数估计中应用正态近似的条件,这对我们接下来的研究也很有启发,要首先清楚成数的具体含义和条件才能更好的研究[1]。2012年黄良文等在《统计学》一书中介绍了正态近似法(Z估计法)对总体成数的区间估计方法,但此方法的使用必须满足大样本条件,而在小样本的情况此方法便无能为力了,这就促使我们寻找适应性更好的区间估计方法[2]。朱惠健通过抽样分布理论,用T估计法对总体成数的区间估计方法(Z估计法)进行修正[3]。我们发现这些方法都是基于大样本理论基础上的正态近似方法,针对区间估计,我们可以从构造新的统计量入手,但是此方法的难度是相当大的,于是想从小样本理论出发,找出更理想的方法对总体成数进行区间估计。
近年来国内外已经开始研究小样本理论,此理论方法的应用可以大大提高效率,减少误差。自从Daniels提出鞍点逼近以来,小样本情况得到了进一步发展,此方法在样本量很小的情况,鞍点逼近的效果明显要高于正态逼近[4]。1994年,Barndorff-Nielsen和Cox推导出极大似然估计密度函数的鞍点逼近式,推动了鞍点逼近方法在统计学中的广泛应用[5]。Casella使用傅立叶反演公式和埃奇沃斯展开,推导出鞍点近似于单个随机变量的密度,并且还展示了用于近似指数族中最大似然估计密度的技术[6]。Butler系统地介绍了鞍点逼近的方法和应用,并给出了高阶渐进推理证明[7]。
罗玉波等利用鞍点逼近的方法来近似广义卡方型混合随机变量的密度函数和分布函数,并通过蒙特卡洛模拟将得到的结果与正态近似法得出的结果进行对比,发现鞍点逼近方法整体表现效果出色,尤其是密度函数尾部区域逼近效果更为突出[8]。王玉琢将鞍点逼近法应用到Pareto分布和非中心卡方分布中,给出Pareto分布极大似然估计的密度函数,以及非中心卡方分布的密度函数和分布函数的鞍点逼近式[9]。钱政超等人是在二项采样下利用鞍点逼近方法构造相对风险的置信区间,其研究方法是用两组相互独立的随机变量且服从二项分布的情况下,用其分布参数比构成相对风险(即两种条件下一个事件分别发生的概率之比),然后用鞍点逼近对相对风险的置信区间进行构造,对比并证明了小样本情况下此方法的优越性[10]。孟令宾等人主要是做了二项抽样下优势比(两种条件下各自的优势之比)的研究,并将其应用到流行病学的相关领域中,证明鞍点逼近法(特别是在小样本情况下)对优势比的区间估计较其他方法精确[11]。
对总体成数的区间估计通常是用正态近似法,但此方法在小样本情况下估计的效果差强人意。所以本文引入枢轴量法和鞍点逼近方法对总体成数进行区间估计,基于鞍点逼近法的小样本特点,本文将其应用在总体成数置信区间的估计,并将其与正态近似法、枢轴量法进行对比,然后进行模拟和实例分析得出:鞍点逼近法较其他方法对总体成数的区间估计效果较优,特别是小样本条件下,估计的区间长度和覆盖率整体表现最佳。相比钱政超和孟令宾等人的研究,本文的研究对象发生了变化,并将该方法应用到对医疗事故发生率的研究中,本研究具有理论和现实意义。
二、总体成数置信区间的构造方法


(1)

(2)
已知总体成数服从二项分布,沿着这条主线再结合二项分布的性质和特点可以对总体成数的置信区间进行构造。本文分别从枢轴量累计分布法、正态近似法(Z估计法和T估计法)和鞍点逼近法对成数的置信区间进行构造,在进行构造前先介绍本文中用到的两个重要引理。
引理1[12]如果G(t,θ)是θ的连续、严格减函数,那么
(1)关于θ的方程G(T-0,θ)=1-α的解是θ的置信水平为1-α的置信下限;
(2)关于θ的方程G(T,θ)=α的解是θ的置信水平为1-α的置信上限;

引理2[13]设随机变量X~b(n,p),Y~b(m,p),且X与Y相互独立,证明Z=X+Y~b(m+n,p)。
(一)枢轴量累积分布法
由式(1)可得每个样本点服从两点分布,设x1,x2,…,xn是来自参数为p且服从伯努利分布的独立随机样本。结合引理1可求总体成数p的置信区间,首先定义p的充分统计量为:
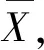
因此,不难验证下列等式成立。
(3)


=Be(p|k,n-k+1)
(4)


同理可得置信上限为:
(二)正态近似法
假设xi相互独立,在大样本下(np>5,n(1-p)>5),利用中心极限定理,则可把二项分布问题转化成正态分布问题近似地去求解,但是目前这种正态近似法并不能保证对置信区间的可信度和准确性,在实际计算中很可能造成难以接受的误差,而为了减少误差我们目前唯一的办法只能使样本量尽可能的大。
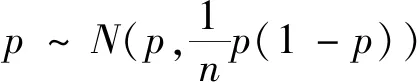
其服从标准正态分布,由于p未知,可用样本方差代替总体方差,则总体成数p的置信水平为1-α的置信区间,为:

2.T估计法[3]。在大样本下,由正态分布的可加性和中心极限定理可得:

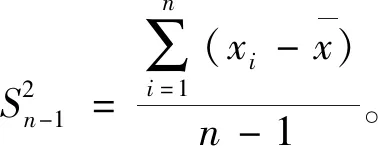
(5)


(6)
将式(6)带入式(5)可得总体成数p的置信水平1-α的置信区间为:
(三)鞍点逼近下总体成数置信区间的构造
鞍点逼近是做渐进分析的一个经常用到的工具,它具有公式简洁、计算效率高和逼近效果更加准确的优点。1999年Goutis系统地介绍了鞍点逼近的理论推导,这里就简单介绍本文用到的鞍点逼近的相关理论基础。假设存在一个非负函数f(x),我们想要在某点x0处逼近它的值。这里需要用到泰勒展开式思想,但是我们不是针对f(x)进行展开,而是在f(x)为正的情况下,使其满足h(x)=lnf(x),即f(x)=eh(x),并选择x0作为展开点,我们得到:
f(x)≈
(7)

(8)


f(x)
(9)
借用公式(9),根据Fourier逆转公式,通过适当的积分变换,可以得到密度函数f(x)的Deniels的鞍点逼近公式为:

采用了Lugannani等人介绍的鞍点逼近公式[14],可以得到累积分布函数的鞍点逼近公式为:
(10)

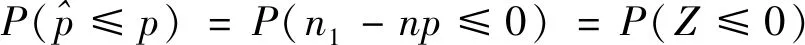
其中,Z=n1-np。根据累积生成函数的逼近方法,首先求出Z的矩生成函数:
φz(θ)=E(eθz)=E(eθ(n1-np))
=E(eθn1)E(e-θnp)
=(peθ+(1-p))ne-θnp
(11)
由式(11)可以求出关于随机变量Z的累积生成函数为:
Kz(θ)=lnφz(θ)=nln(peθ+(1-p))-θnp
因此,可以求出随机变量Z的一阶、二阶导数为:
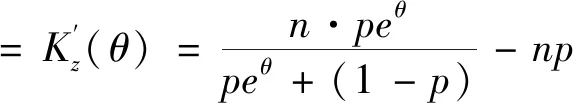
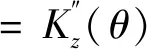
peθ(n-n1)-n1(1-p)=0

三、蒙特卡洛模拟
接下来,我们将通过蒙特卡洛模拟比较枢轴量法、正态近似法(Z估计法和T估计法)和鞍点逼近法对总体成数置信区间的估计效果。关于对置信区间的估计好坏,我们通常用区间长度和覆盖率进行评判,希望得到的覆盖率越高越好,区间长度越短越好。本文主要考虑如下情形:当样本量n=30,50,100,300的情况下,分别对p=0.05,0.25,0.5,0.75的情况进行比较分析,具体模拟结果见表1和表2。

表1 不同的估计方法对总体成数P<0.5时区间估计的模拟结果表

表2 不同的估计方法对总体成数P≥0.5时区间估计的模拟结果表
对蒙特卡洛模拟的结果进行分析可以得到:小样本情况下,即n=30,50的情形,鞍点逼近法较Z估计法和T估计法的区间长度短,并且覆盖率近次于枢轴量法。Z估计法虽然较T估计法区间长度短,但有时候覆盖率表现并不是太理想。较大样本情况下,即n=100,n=300的情形,随着p的增大,鞍点逼近的区间长度略有增加,但相比其他三种方法仍然是最短置信区间长度,整体表现最优。此外,这几种方法普遍更适用于小概率事件。
四、实例分析
近年来,医疗事故频繁发生,其发生率是一个重要的指标,它反映了医疗机构的工作人员对工作认真负责的态度。这里列举两个例子,对医疗机构医疗事故的发生率进行实例研究,让更多的人认识到问题的严重性,政府部门应该加强监管力度,患者应到医疗事故发生率比较低的医疗机构就医。为了更加精确地算出相关医疗事故的发生率,这里比较了上述四种置信区间的构造方法,具体应用如下。

通过上面的三种方法分别构造p的95%的置信区间见表3。表3表明:小样本下,枢轴量累积分布法求出的置信区间比较可靠,但区间长度太大;Z估计法和T估计法的区间长度很接近,但相比鞍点逼近方法,鞍点逼近法求出的p的覆盖率较高,区间长度最短。

表3 不同估计方法对妇产科医疗事故发生率的区间估计结果表
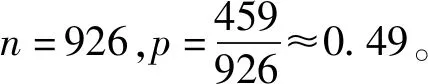
通过上面的三种方法分别构造p的95%的置信区间,见表4。由表4可知,大样本情况下,鞍点逼近在区间长度上有明显的优势,覆盖率仅次于枢轴量法。

表4 不同估计方法对医疗机构责任比率的区间估计结果表
五、结 论
本文重点介绍了用枢轴量法和鞍点逼近法构造的总体成数的置信区间,并通过模拟得出如下结论:枢轴量法的覆盖率较高,但区间长度较长,在实际应用中并不是较好的选择;相比正态近似法对总体成数的区间估计方法,鞍点逼近法无论是在平均区间长度,还是在覆盖率上都表现出明显的优势,尤其是在小样本情况下,鞍点逼近法对总体成数置信区间的估计精度明显提高,是一种较好的区间构造方法。另外,研究结果表明,这几种方法普遍适用于小概率事件,特别是正态近似法和鞍点逼近法。通过对两个医疗事故发生率的实例分析,我们认为,根据抽样分布理论对医疗事故发生率的研究,可以转化到对总体成数的估计问题,研究结果表明,鞍点逼近法构造医疗事故的发生率有较好区间估计效果,特别是对一些小概率、小样本事件的研究,此方法具有普遍适用性。
本文的创新之处主要是运用鞍点逼近法对总体成数的置信区间进行估计,并且通过蒙特卡洛模拟和实例分析,将其与正态近似法、枢轴量法进行比较。本文的研究不足之处是在模拟过程中,当抽取的样本较少并且成数的值也较小时,容易出现抽不到所需样本的情况。

