泊松提升模型在中国车险索赔频率预测建模中的应用
张连增,申 晴
(南开大学 金融学院,天津 300350)
一、引 言
车险是非寿险的重要组成部分,车险定价一直是一个复杂、困难并且重要的工作。自从20世纪90年代英国精算师把广义线性模型(GLM)应用到非寿险定价中,非寿险产品得以科学定价的同时,GLM在精算中的应用也得到不断完善与发展。随着大数据时代的到来,在车险产品定价过程中需要考虑的因素特别是数值型变量因素的不断增加,传统GLM的局限性不断凸显,主要表现为:随着变量的增多,变量间的相关关系增强,GLM的预测能力不断下降。为此,在建立GLM之前,需要对样本中的数值型解释变量调整为分类变量,而且为减少可能存在的具有相关关系的解释变量对GLM预测效果的影响,在建立GLM时,需要引入交互项。在互联网科技迅速发展的今天,上述数据处理与操作可以轻松实现,但是经过类似处理与操作后的模型有效性问题值得思考。
为了克服GLM自身存在的局限性,当前在车险产品定价中出现了很多模型与方法,其中以回归树、支持向量机、神经网络和Boosting算法等为代表的机器学习方法,近年来得到了快速的发展。本文将Boosting算法加入到SBS(Standardized Binary Split)回归树模型中,应用得到的模型对中国交强险索赔频率进行预测建模分析。然后将泊松提升模型与SBS回归树模型进行比较,以损失函数的最小化为标准来选择相对较优的模型,应用得到的较优模型对中国交强险保单中的各个变量进行单因素预测分析,分别分析各个因素对索赔频率的影响。本研究为以后的相关研究和交强险定价提供一定的理论借鉴和参考。
二、文献综述
本文中用到的泊松提升模型是Boosting算法与SBS回归树的结合,关于Boosting算法和回归树方法在车险产品定价中应用的国内外相关研究成果主要有:
Friedman最早提出了一种梯度提升法(GBM),它通过对回归型问题的求解来扩展提升能力,该算法成功地将可加性建模和极大似然等统计元素纳入建模中,被认为是数据挖掘领域的重大突破[1]。Guelman使用梯度提升树(Gradient Boosted Trees,GBT)对索赔频率和索赔强度分别进行建模,该模型对索赔频率和索赔强度的预测效果比传统广义线性模型的预测效果要好[2]。Liu等将一种称为多分类AdaBoost树方法用于车险索赔频率预测分析,并将该模型与广义线性模型、神经网络模型与支持向量机模型进行比较,最后证明多分类AdaBoost树方法具有更强的预测能力和可解释性[3]。Zöchbauer认为回归树方法为构建具有相似风险特征的同质投资组合提供了一个有用的工具,更先进的树集成方法,如Bagging法和随机森林的预测能力超过了传统的广义线性模型[4]。Wüthrich基于驾驶者行为数据对车险产品价格的稳定性进行研究,认为使用经典的回归树或Boosting算法进行价格更新时,所得到的价格波动较大,为了使价格更新顺利进行,建议使用以前的费率结构作为新产品的初始价格[5]。Noll等基于第三方责任保险数据集,比较了经典广义线性模型、回归树建模、助推器和神经网络方法在索赔频率预测建模中的表现,研究表明:广义线性模型不能恰当地处理特征分量之间的交互作用,而其他方法能够较好地处理这些交互影响[6]。
张连增等应用回归树方法对中国车险索赔频率进行预测建模分析,并与广义线性模型进行比较,得出单棵回归树的预测能力不如传统的广义线性模型,但是通过Bagging法得到的回归树优于传统的广义线性模型[7]。孟生旺等通过应用随机森林模型、神经网络模型和XGBoost模型对驾驶行为风险因子的出险概率进行分析研究,并与传统的logistic回归模型进行比较,结果表明XGBoost模型对于出险概率的预测能力更强[8]。
除此之外,关于车险费率厘定还有其他一些研究成果,例如,张连增等在车险费率厘定时提出了一种处理大额索赔的频率—强度方法,并通过分别对索赔频率和索赔强度进行建模分析实证检验了带有大额索赔的频率—强度模型在车险费率厘定中的优越性[9]。
总结国内外研究成果发现:第一,Boosting算法和回归树模型在车险定价应用的研究成果很多,国内相关的研究成果则较少;第二,国内外关于Boosting算法和回归树的研究大多侧重于二者在车险定价中的比较,关于将Boosting算法加入到回归树模型中除了国外有少量研究外,其他相关研究较少。鉴于此,本文采用Boosting算法与SBS回归树相结合的方法对中国车险定价索赔频率进行预测分析研究。
三、模型介绍

本文应用泊松提升模型(Poisson boosting model)进行索赔频率建模。泊松提升模型是在以泊松偏差统计量为损失函数的SBS(Standardized binary split)回归树模型中加入Boosting算法。具体步骤为:将一棵只有很少叶子的SBS回归树作为弱估计量,以这个弱估计量的残差作为新的响应来构造下一个弱估计量,以自适应的方式迭代此过程则将产生一个较强的估计量。以下重点介绍SBS回归树模型、Boosting 算法和泊松提升模型这三部分内容。
(一)SBS回归树模型
SBS回归树模型就是在给定一个复杂性参数(complexity parameter)的条件下,寻找对特征空间X的最优区分(Xk)k=1,2,…,K,其中K表示叶子数。对特征空间的最优区分就是在所有的SBS中迭代寻找最优的分割[10]。
(二)Boosting算法
Boosting算法是一种将弱学习器(weak learner)提升为强学习器的算法[11]。
(三)泊松提升模型
1.模型介绍
泊松提升模型将Boosting算法加入到SBS回归树模型中,主要是通过自适应迭代的方法实现样本内损失函数的最小化,其算法流程如下:
(1) 初始化
a.选择K≥2和固定α∈(0,1],其中K表示叶子数,α表示收缩因子(通常为1)。
(2) 重复。当m=1,2,…,M
(1)
其中n为样本个数。
b.构建一个SBS泊松回归树估计
(2)
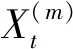
c.更新估计值

(3)
(3)频率估计值
(4)
2.模型估计
将K=2作为Boosting算法的初始值,则此时的回归树估计值表示为:
(5)
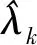
(6)

(7)
所以初始的索赔频率模型假设被替换为:
(8)

(9)
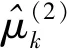
(10)
(11)
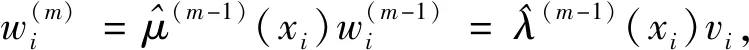
(12)
i=1,2,…,n

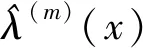
(13)
四、实证分析
(一)数据描述
本文数据来源于国内某保险公司交通事故责任强制保险486 780条理赔数据,数据的格式如表1所示。

表1 数据格式表
关于数据中变量的说明如表2所示:
从486 780条数据中随机抽取390 000条(后面回归树建模分析中的参数minbucket=6 000,这样可以保证训练集中至多可以分成65组)样本作为训练集进行建模,记为L={(Ni,xi,vi):i=1,2,…,n},其中xi表示训练集中各个变量,n=390 000,用于模型的拟合和选择。剩余96 780条样本主要用于模型的预测分析,记为T={(Nt,xt,vt):t=1,2,…,n′},其中n′=96 780。

表2 变量说明表
(二)变量的描述性统计
由上部分可知,本文将样本数据分为训练集和测试集。通过比较训练样本和测试样本的索赔次数和索赔频率,我们发现二者是有区别的。具体情况如表3所示。表3反映了训练集和测试集在索赔次数和索赔频率方面的比较情况,其中索赔次数分别为:0、1、2、3、4的样本数占训练集和测试集的比率各有不同,具有一定的差异。在索赔频率方面:训练集的索赔频率为5.173 623%,略低于测试集的索赔频率(5.285 29%)。训练集和测试集的索赔次数和索赔频率的差异会造成二者损失函数值的差异,影响模型的效果,具体如下节所示。

表3 训练集和测试集的索赔次数和索赔频率情况表
(三)实证结果
1.SBS回归树模型
(1)树的生成。基于SBS回归树模型对训练集L进行建模,该算法通过用R软件包中的rpart函数进行循环迭代来实现。关于函数rpart的相关参数首先进行简单介绍,其中,minbucket表示生成的回归树中每片树叶至少应该包含的数据记录个数,取minbucket的值为6 000[4]。cp(complexity parameter)为复杂性参数,控制树的规模,取值范围为(0,1],其值越小则树的规模也就越大,此处我们设置cp的初始值为0.000 5,关于参数cp进行赋值的详细介绍参考Therneau等[12]。我们称经过上述参数设定生成的模型为RT1,生成的树为tree1,树的生成通过运行summary函数可得:生成的SBS回归树一共有9片叶子和8次分割,其中第一个分割考虑的是无赔款优待水平(BonusMal)是否为A、B、H类。通过观察图1,可以发现第一个分割是最有效的分割,因为第一个分割使样本内损失从0.225 667 6下降到0.222 932 3,相对于其他分割来说,第一个分割使样本内损失下降的最多。
通过图1,我们分析了cp值为0.000 5,叶子数为9、分割次数为8的回归树模型及其样本内损失减少情况。接下来我们通过10折交叉验证方法来进一步决定树的最优规模和相应的样本内损失。

图1 RT1模型样本内损失减少情况图
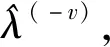

重复上述过程,可以得到10折交叉验证误差:
运用上述10折交叉验证原理,我们首先设置cp=10-8(初始值设置尽可能小)来生成一个规模较大的SBS回归树,我们称这个回归树为tree2,这个回归树一共有K=35片叶子。对tree2进行10折交叉验证,根据最小交叉验证误差规则,判断模型tree2是否为最优子树,我们称这个模型为RT2。回归树tree2的交叉验证误差和相应的标准误差条如图2a所示:

a.模型RT1
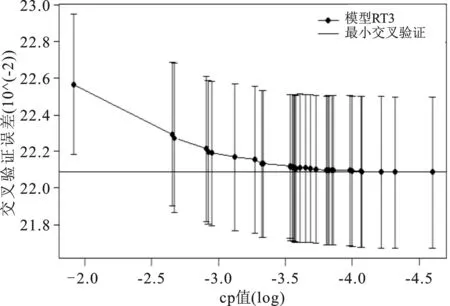
b.模型RT2图2 模型RT2和RT3的10折交叉验证情况图
通过观察图2a可以发现:交叉验证误差(CV error)在成本复杂性参数(cost-complexity parameter)接近-5时达到最小,在-8时交叉验证误差不变,因此RT2存在严重的过拟合问题。通过选择最小的交叉验证误差以及对应的cp值,重新生成树tree3以及对应的最小交叉验证规则模型为RT3,树tree3共有35片叶子,如图2b所示,cp=2.520 53e-04时有最小的10折交叉验证误差,也不存在过拟合现象,可以认为RT3是最优子树。
下面结合上一节所述的样本内和样本外损失函数的表达式,我们分别计算RT1、RT2、RT3的样本内和样本外损失,具体情况如表4所示:
表4三种回归树模型的样本表单位:10-2

样本内损失样本外损失RT1(9片叶子)22.0858822.54131RT2(35片叶子)21.9737022.49499RT3(35片叶子)21.9737022.49499
从上表我们发现模型RT2的样本内外损失和模型RT3的一样,但都低于模型RT1的相关水平,初步可以认为回归树规模越大(即叶子数越多),则回归模型的样本偏差越小,损失也就越小。虽然模型RT2的样本损失和模型RT3的相关损失一样,但模型RT2设置的初始cp值过小,可能会存在过拟合问题,模型RT3是通过10折交叉验证方法验证得到的最优模型。理论上最优子树的选择很重要,不仅能提高模型的效果,也能减少过拟合问题。
2.泊松提升回归模型
考虑用Poisson Boosting Machine Model(泊松提升模型)进行索赔频率建模。泊松提升模型是基于以泊松偏差统计量为损失函数的SBS(Standardized Binary Split)回归树算法。该算法通过用R软件包中的rpart函数进行循环迭代来实现。本文把J=1的泊松Boosting 算法模型称为模型PBM1,通过编程计算得到模型PBM1的样本内外损失分别为:21.984 28×10-2和22.466 05×10-2,此时模型PBM1的样本内损失高于模型RT3的样本内损失,而模型PBM1的样本外损失却低于模型RT3的样本外损失。为了改善模型的样本内损失情况,不仅可以增加迭代次数M,而且还可以增加树的深度J,或者两者同时增加,从图3发现3个模型随着迭代次数的增加,样本内损失减少的曲线比较平滑,所以本文中主要分析增加树的深度对模型样本内损失的影响。在保证算法运行速度的前提下,又不至于使模型出现过拟合的问题,我们选择的迭代次数M值相对较小。同理,我们把J=2,3的泊松Boosting 算法模型分别称为模型PBM2,PBM3。汇总模型PBM1,PBM2,PBM3与RT3的各种样本内外损失情况如表5所示。

表5 三种泊松Boosting算法模型和模型RT3样本损失情况表 单位:10-2
通过表5发现:模型PBM3(J=3,M=20)的样本内损失低于模型PBM3(J=3,M=15)的样本内损失,而该模型的样本外损失却高于模型PBM3(J=3,M=15)的样本外损失,说明当迭代次数M=20时,模型PBM3存在过拟合问题。所以PBM3的最大迭代次数M=15。在模型PBM1和模型PBM2不存在过拟合问题的前提下,为了便于比较分析,本文中确定模型PBM1和模型PBM2的迭代次数M=10。
通过比较模型PBM1(J=1,M=10)与PBM2(J=2,M=10),不难发现PBM2的样本内外损失低于PBM1的相关样本损失情况,说明在迭代次数M保持不变的情况下,随着树的深度J的增加,模型的样本内外损失情况不断减小,模型得到优化。同理,通过比较模型PBM3(J=3,M=15)与PBM2(J=2,M=10),PBM1(J=1,M=10)的表现,发现模型PBM3的样本内外损失情况低于PBM2与PBM1的相关样本损失情况,说明在不存在过拟合问题的前提下,该模型随着树的深度J和迭代次数M的同时增加,模型的样本内外损失情况是不断减小的,模型得到进一步的优化。相对于PBM1(J=1,M=10),PBM2(J=2,M=10)和RT3而言,PBM3(J=3,M=15)的样本内外损失是最小的,模型PBM3是最优的模型。
PBM1 (J=1,M=10),PBM2(J=2,M=10),PBM3(J=3,M=15)和RT3的样本内损失情况如图3所示:
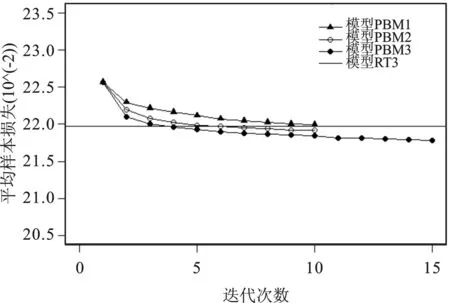
图3 三种不同泊松Boosting算法模型和RT3的样本内损失情况图
图3中三角形表示模型PBM1的样本内损失情况,空心圆表示模型PBM2的样本内损失情况,实心点表示模型PBM3的样本内损失情况,实线表示模型RT3的样本内损失情况。通过观察上图发现,虽然模型PBM1(J=1,M=10)的样本内损失随着迭代次数的增加而不断降低,但是始终高于模型RT3的样本内损失。由于模型PBM1的深度和迭代次数较小,使得模型PBM1的表现不如模型RT3。在保持模型PBM1的迭代次数M=10不变的情况下,增加树的深度到J=2则得到模型PBM2。从上图容易发现模型PBM2在迭代到第5次时,样本内损失已经低于模型RT3的样本内损失,在保持迭代次数不变的情况下,增加树的深度,使模型的样本内损失不断减少,模型得到优化。同理,在树的深度增加到J=3以及迭代次数增加到M=15时得到模型PBM3,相对于模型PBM1,PBM2而言,随着每次迭代的进行,模型PBM3的样本内损失减少的更快,且在迭代到第4次时,模型PBM3的样本内损失已经低于模型RT3的样本内损失情况。所以,在模型PBM1、PBM2、PBM3和模型RT3四个模型中,模型PBM3的样本内外损失最小,模型PBM3是相对较优的模型。
3.模型的预测分析
通过上述分析,选择相对较优的泊松提升模型PBM3,用测试集T对模型PBM3进行单变量预测分析。在进行预测分析之前,确定不同变量在测试集中出现次数最多的数值或因素为各个变量的固定取值,具体为:保单省份(Region)为P37,驾驶员年龄(DrivAge)为50,驾驶员性别(Gender)为M,汽车座位数(Seat)为5,汽车重量(Weight)为2,汽车车龄(VehAge)为6,无赔款优待水平(BonusMalus)为A,转续保(renew)为Ri,车系(VehBrand)为C。对某一变量(例如变量Region)进行单变量预测时,该变量的数据为测试集中的观察值,其他变量的数据则全部为对应变量设置的初始固定值。其中各个变量的预测情况如图4所示。上面各个图中,横坐标表示对应各个变量的分组情况,纵坐标表示各个变量不同分组对应的预测频率大小。
从保单省份(Region)频率预测情况图中,我们发现:在其他因素不变时,各个省份的交强险索赔频率的预测值不同,其中索赔频率最高的省份P43(湖南省)为0.078 5,索赔频率最低的省份P50(重庆市)为0.029 1。由于各个地区社会、经济、文化、气候以及地理环境的差别,使得各个省份的交强险索赔频率出现差异。所以,在未来的交强险定价工作中,也应将地区因素作为一个定价因子加以考虑。
从汽车车龄(VehAge)频率预测情况图发现:在其他因素不变时,索赔频率大体上随着汽车车龄的增加而增大。具体表现为:在汽车车龄为0~2时,索赔频率为0.038 4,达到了最小,除了在汽车车龄为6时出现了较小的波动外,其余的索赔频率总是随着汽车车龄的增加而增大的,特别是当汽车车龄大于11时,索赔频率达到了最大为0.065 6。说明在其他条件不变的情况,新车由于机器设备性能较好,此时驾驶的安全性较高,出事故的概率则较小,反之,旧车随着机器设备的老化等原因使驾驶的危险性较高,出事故的概率则较大。

图4 各个单变量预测结果图
从驾驶员车龄(DrivAge)频率预测情况图中,我们发现:在其他因素不变时,驾驶员年龄在18~46时,索赔频率呈缓慢下降的趋势,其中驾驶员年龄为18~24时索赔频率为0.073 5,达到了最大,年轻的驾驶员由于驾驶经验缺乏、年轻气盛、爱开“冲动车,斗气车”等原因,导致出事故的概率较大,索赔频率较高。随着年龄以及驾驶经验的增加,中年人出事故的概率较小,索赔频率较小。另外,驾驶员年龄在47~80时,索赔频率又有增加的趋势,特别是55~80的驾驶员,随着年龄的增加,应急能力下降,导致出事故的概率增加,索赔频率较大。
从汽车座位数(Seat)频率预测情况图中,我们发现:在其他因素不变时,汽车座位数在小于6座时,索赔频率为0.050 49,相对较低,在大于等于6座时,索赔频率为0.054 5,有所增大。
从驾驶员性别(Gender)频率预测情况图中,我们发现:在其他因素不变时,男性的索赔频率(0.050 486)低于女性的索赔频率(0.053 092 261)。由于身体和心理原因使得女性出事故的概率大于男性,索赔频率高于男性。同时,相关研究表明:女性出小事故的概率高于男性,但是男性出致死或较大损害事故的概率高于女性。
从汽车重量(Weight)频率预测情况图中,我们发现:在其他因素不变时,索赔频率随汽车重量的增加而增大,汽车重量低于0.5时,索赔频率为0.030 3,达到了最小;在汽车重量为1时,索赔频率为0.035 2;当汽车重量大于等于2时,索赔频率为0.039 7,此时索赔频率达到了最大。
从无赔款优待水平(BonusMalus)频率预测情况图中,我们发现:在其他因素不变时,无赔款优待水平越高,即历史索赔次数越少,则索赔频率越低。其中,无赔款优待水平为G(上年度发生两次及两次以上有责任交通事故)时,索赔频率最高为0.108 3,而无赔款优待水平为H(上年度发生有责任道路交通死亡事故)时,索赔频率最低为0.037 9,主要是因为本文中H类的索赔保单的索赔次数都是0次,所以本文预测的索赔频率相对较小。
汽车类型(Veh Brand)所有不同分类的索赔频率都为0.050 485 767,初步分析由于样本数据中C系车的样本数为89 908个,占测试样本集的绝大部分,文章中该车系的索赔频率影响了其他车系的索赔频率。同样,转续保(renew)所有索赔频率一样,都为0.050 485 767。
五、结 论
本文将Boosting算法加入到SBS回归树模型中,并且比较Boosting算法加入前后模型效果的变化情况,得到相对较优的模型,并用较优的模型对测试集进行单变量索赔频率预测分析。在模型选择和索赔频率预测分析的过程中总结得出以下结论:
第一,模型RT3是通过10折交叉验证方法得到的最优子树,其表现优于模型RT1和RT2,在回归树分析中,剪枝等处理工作对确定最优子树很必要。在模型RT3中加入Boosting算法得到了泊松提升模型,至于泊松提升模型,在保证不存在过拟合问题的前提下,随着树的深度和迭代次数二者中的其一或者二者同时增加,则模型效果不断得到改进。基于本文中的训练集,最终确定了深度为3,迭代次数为15的模型PBM3为最优模型。
第二,通过用测试集对模型PBM3分别进行单变量预测分析我们得到:在其他因素不变的条件下,由于各个省份(Region)社会、经济和自然环境的差异,使得各个省份的交强险索赔频率各不相同;索赔频率大体上是随着汽车车龄(VehAge)的增加而增大的;驾驶员车龄(Drivage)为18~24时的索赔频率最高,即年轻人的索赔频率最高,老年人的索赔频率次高,中年人的索赔频率最低;汽车座位数(Seat)小于6座的索赔频率低于汽车座位数(Seat)大于等于6座的索赔频率;男性的索赔频率低于女性的索赔频率;索赔频率随汽车重量(Weight)的增加而增大;无赔款优待水平(BonusMalus)越高,即历史索赔次数越少,索赔频率则越低。

