高浓度锌离子背景下检测痕量镍离子的扩展卡尔曼滤波优选方法

周风波 李勇刚 朱红求

摘 要：在锌湿法冶金的净化过程中，锌离子（Zn2+）与痕量镍离子（Ni2+）的浓度比高达105，且Zn2+与Ni2+谱峰重叠严重，使得Ni2+信号被高浓度锌信号完全掩蔽，导致Ni2+的灵敏度较低，以及Ni2+的吸光度和浓度呈现出很强的非线性关系。针对高锌溶液中Ni2+浓度难以检测的问题，本研究提出了一种基于紫外可见吸收光谱在高锌背景下检测Ni2+的扩展卡尔曼滤波（EKF）波长优选的方法。首先制备Ni2+标准溶液，建立Ni2+的非线性模型，获取吸光系数矩阵;然后通过设置相关系数阈值方法选择滤波区间，最后通过扩展卡尔曼滤波分光光度法检测Ni2+浓度。Ni2+浓度的检测范围为0.3～6.0 mg/L，预测均方根误差（RMSEP）为0.145，平均相对偏差为3.86%。 本方法快速、 简单， 适用于锌湿法冶金净化过程中Ni2+的实时检测和控制。

关键词：紫外可见吸收光谱法; 扩展卡尔曼滤波; 波长选择; 锌湿法冶金; 镍离子

1 引 言

在锌湿法冶金的净化过程中，冶金液含有大量锌离子（Zn2+）和各种痕量杂质离子，Zn2+与痕量离子浓度比高达105，冶金液呈现高浓度比和痕量多金属离子共存的特点[1，2]。杂质离子的存在不仅影响生产效率和产品质量，而且浪费资源。在实际生产中，冶金液杂质离子的浓度主要依赖人工离线分析，检测滞后，调整盲目，导致生产指标波动大，产品质量不合格，造成浪费。因此，研究在线检测锌溶液中的杂质离子的方法具有非常重要的理论和实际意义[3～5]。近年来，已有在线测定金属离子的方法，例如电位滴定法、极谱法、电感耦合等离子体质谱法、紫外可见吸收光谱法和激光诱导击穿光谱法等，其中，紫外可见吸收光谱法以其简单、准确、快速、多功能和低成本等优点，在分析检测领域广泛使用[6～10]。

紫外可见吸收光谱法作为一种常规的定量分析方法，广泛应用于溶液中金属络合物的测定，从而测定金属离子浓度。目前，研究者已经提出了多种分光光度法用于金属离子的检测，如多波长线性回归分析（MLRA）、差分分光光度法、主成分回归（PCR）、导数分光光度法、卡尔曼滤波分光光度法和偏最小二乘回归（PLSR）等[11～16]。然而，这些方法通常适用于分析浓度相近的离子，但针对高浓度比溶液的在线分析的方法未见报道。对于湿法冶金生产中的高浓度Zn2+溶液，Zn2+与痕量Ni2+的浓度比可高达105，在线检测Ni2+存在如下问题：Ni2+信号被高浓度Zn2+信号掩蔽，灵敏度较低，吸光度较小; Ni2+的吸光度和浓度呈现出很强的非线性关系; 由于锌和Ni2+的化学性质相近，导致两者谱峰严重重叠。

卡尔曼滤波分光光度法以最小均方误差为准则，对一系列含有误差的测量数据进行数学处理，适用于多组分体系的分光光度分析，目前主要用于多组分的线性建模[17～19]。针对高锌溶液中Ni2+的非线性问题，本研究在卡尔曼滤波分光光度法的基础上，提出了基于紫外可见吸收光谱法在高锌背景下检测Ni2+的扩展卡尔曼滤波（EKF）波长优选的方法。首先制备Ni2+标准溶液，建立Ni2+的非线性模型，获取吸光系数矩阵; 然后通过设置相关系数阈值方法选择滤波区间，最后通过EKF分光光度法检测Ni2+的浓度。Ni2+的检测范围为0.3～6.0 mg/L，预测均方根误差（RMSEP）为0.145，平均相对偏差为3.9%。本方法快速、简单，适用于锌湿法冶金净化过程中Ni2+的实时检测和产品质量控制。

2 扩展卡尔曼滤波分光光度法

2.1 基本原理

卡尔曼滤波分光光度法可以在线性条件下对分析物浓度进行最佳估计[20～23]。然而，实际系统总是具有不同程度的非线性。扩展卡尔曼滤波分光光度法用于非线性系统的核心思想是：对于非线性系统，将非线性函数通过Tayor级数展开，省略第二级及以上项，获得近似线性化系统模型，然后使用卡尔曼滤波器对分析物进行滤波器估计[24～27]。通常，扩展卡尔曼滤波使用系统状态模型和测量模型描述非线性系统，这两个方程分别表示为：

3 实验部分

3.1 仪器与试剂

T9双光束紫外可见分光光度计（北京普析通用公司）用于测量吸收光谱。T9分光光度计采用混合CT双单器光学系统，配备特殊光栅和高性能PMT接收器，配备Uvwin软件用于控制光谱仪和采集数据。所用试剂均为分析纯。

3.2 實验方法

在25 mL校准烧瓶中，加入一系列20～30 g/L Zn2+和0.3～6.0 mg/L Ni2+的混合标准溶液，以及7.5 mL乙酸乙酸钠缓冲溶液（pH=5.5）和5.00 mL亚硝基R盐溶液，并用适量蒸馏水稀释至标定刻度。以相同方式制备空白溶液。T9分光光度计使用1 cm石英比色皿，以试剂空白溶液作参比测量吸收光谱，扫描范围为250～600 nm。所有的测量光谱取5次重复测量的平均值，用于后续分析。

4 结果与讨论

4.1 紫外可见吸收光谱曲线

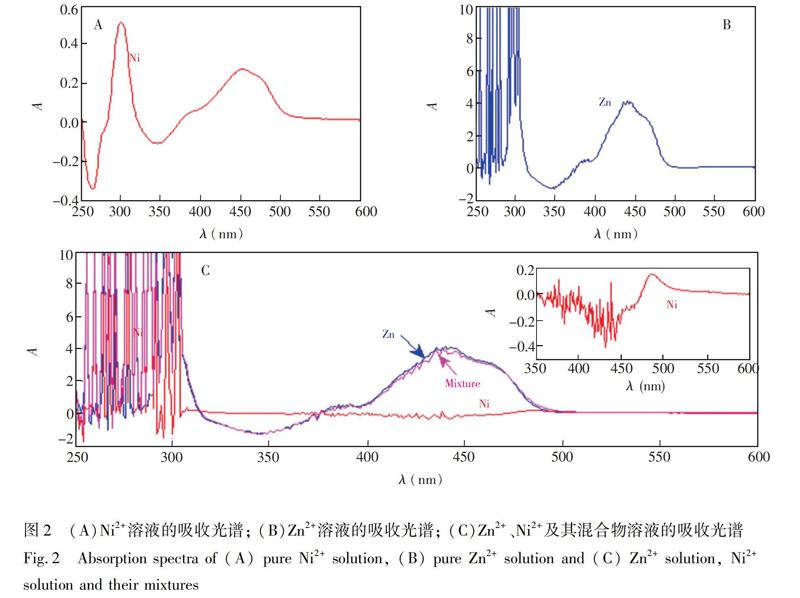
紫外可见吸收光谱法检测的基本原理为朗伯比尔定律，即一束平行单色光通过某一均匀有色溶液时，当光程固定时，溶液的吸光度和溶液浓度成正比。图2A为0.6 mg/L Ni2+溶液的吸收光谱，分别在波长为302和455 nm处出现特征峰，最大吸光度为0.51。图2B为20 g/L Zn2+的吸收光谱，在波长441 nm处出现特征峰，最大吸光度为4.149。图2C为Zn2+（20 g/L）、Ni2+（0.6 mg/L）及其混合物在250～600 nm波长范围内的吸收光谱。由图2C可见，Zn2+的吸光度接近其混合物的吸光度，几乎完全掩蔽Ni2+信号，导致Ni2+的吸光度较低; 从Ni2+的局部放大图可见，受高浓度Zn2+影响，Ni2+的特征峰发生偏移，在波长为486 nm处出现特征峰且最大吸光度仅为0.15。在250～300 nm的波长范围内，由于Zn2+过饱和，吸光度超出仪器测量范围，所测数值不可用。由于锌和镍具有相近的化学性质，在整个波长范围内，Zn2+和Ni2+的吸收光谱严重重叠。因此，在高锌溶液中检测Ni2+浓度难度大。

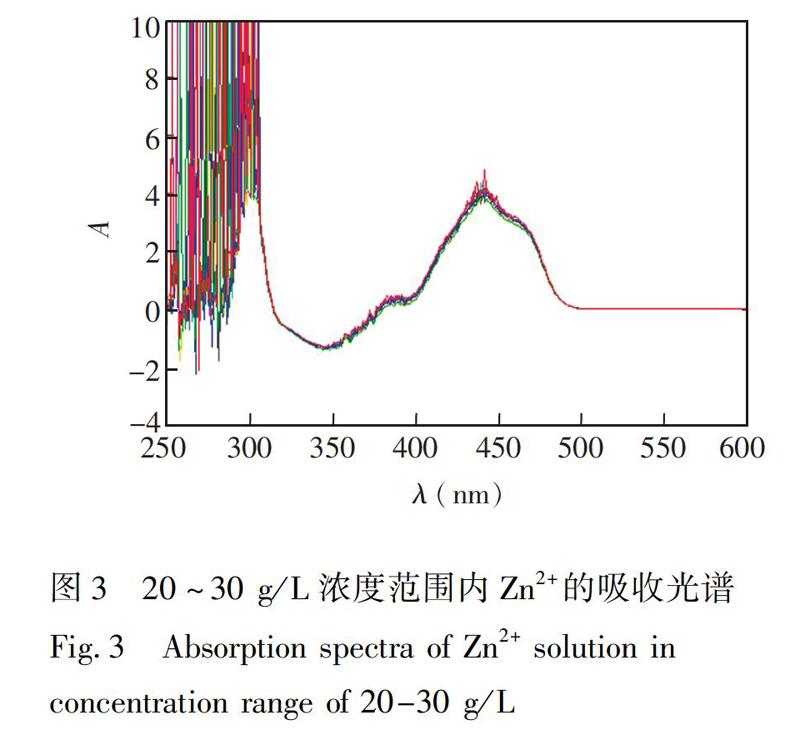
Zn2+浓度在20～30 g/L范围的吸收光谱如图3所示，随着Zn2+浓度的增加，吸光度几乎不变。其原因是Zn2+浓度过饱和，其吸光度与浓度的关系不再服从朗伯比尔定律。因此，将Zn2+浓度固定在20 g/L，用于之后的分析。

4.2 镍的校正曲线

为了评价高锌溶液中痕量Ni2+的线性行为，以20 g/L Zn2+溶液为参比，配制20组0.3～6.0 mg/L的Ni2+标准溶液，使用Ni2+在最大峰值（波长为486 nm）的吸光度与相应的浓度构建校正曲线，分别使用线性和非线性模型进行校正，校正曲线如图4所示。图4A为以20 g/L Zn2+为参比，不同浓度Ni2+的20组标准溶液吸收光谱曲线。由Ni2+线性校正曲线（图4B）可见，Ni2+的线性性很差。图4C为Zn2+在486 nm处的非线性校准曲线，使用四阶多项式拟合，拟合效果较好，相关系数R=0.9913，拟合系数为＼[0.0037，0.0448， 0.1760，0.2303， 0.2054＼]。

4.3 扩展卡尔曼滤波波长优选

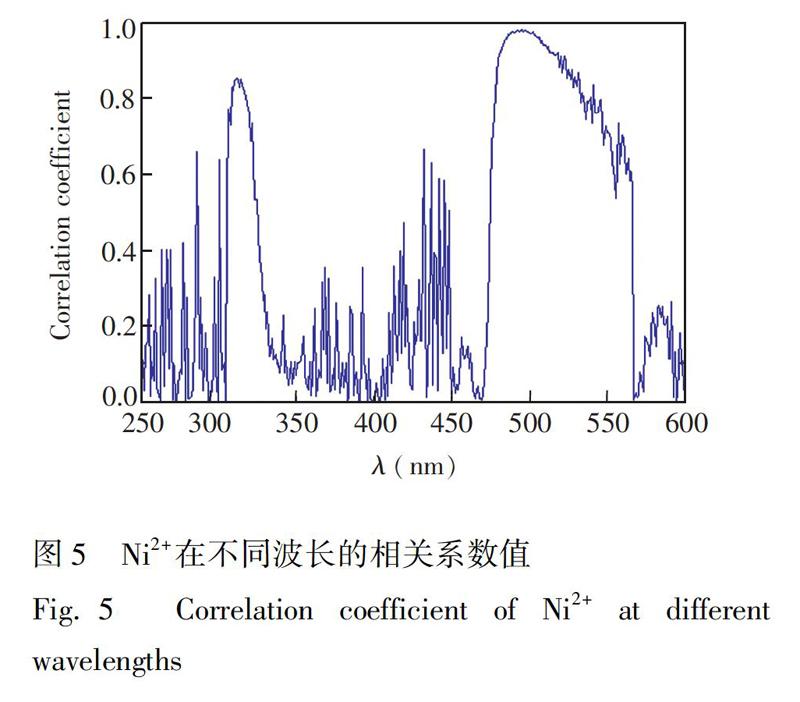
采用相关系数R作为扩展卡尔曼滤波分光光度法的波长优选方法指标， 相关系数R值越大，表明此波长对扩展卡尔曼模型的贡献越大，反之，则对模型的贡献较小。根据Ri值的大小对波长进行排序，选择Ri值较大的波长进行EKF建模。Ni2+在不同波长的相关系数值如图5所示，在大部分波长下，Ni2+相关系数R较低，对模型贡献较低。只有在465～515 nm的波长范围内，相关系数R>0.92，因此选择此段波长作为EKF滤波区间。

4.4 扩展卡尔曼滤波法检测Ni2+的浓度

配制一组0.6 mg/L Ni2+的标准溶液，通过扩展卡尔曼滤波检测Ni2+的浓度曲线如图6所示，滤波区间为465～515 nm，Ni2+的标定值由水平线表示。由图6可见，随着滤波点增加，滤波器值（即定量检测的浓度）趋于稳定。在滤波初始阶段，滤波检测值波动很大，非常不稳定; 在经过15～30次滤波后，滤波器检测值逐渐趋于稳定; 在35～45滤波区间，滤波器值已经稳定，并且可以停止滤波。Ni2+的最终检测浓度为0.5929，非常接近标定值。通常，如果选择合适的滤波区间，则经过20～50次滤波可获得稳定的检测值。

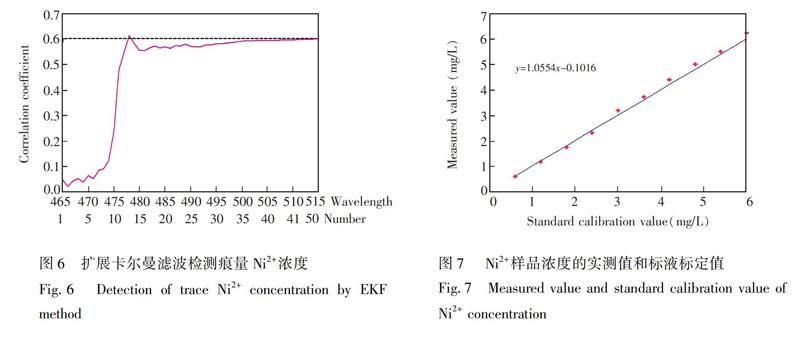
為了评价扩展卡尔曼滤波器的性能，制备了10组不同浓度（0.6～6 mg/L）Ni2+溶液。Ni2+样品浓度实测值和标液标定值（图7）几乎完全一致。 通过实验数据计算，校准方程为y=1.0554x-0.1016，Ni2+浓度的预测均方根误差（RMSEP）为0.145，平均相对偏差为3.9%，方法的性能指标满足实际生产的要求（平均相对偏差≤10%）。

References

1 Zahmatkesh M， Spanjers H， van Lier J B. Environ. Technol.， 2017， 38 （21）： 1-11

2 Mahmoudpour M， Pilevar Z， Javanmardi F. Anal. Methods，  2018，  10 （20）： 2398-2404

3 Arroz E， Jordan M， Dumancas G G. Appl. Spectrosc.，  2017，  71 （7）： 1633-1639

4 Han J， Yang C， Zhou X. Hydrometallurgy，  2017，  173： 134-48

5 Jarosz P， Kusiak J， Maecki S. Arch. Civ. Mech. Eng.，  2018，  18（4）： 1116-1122

6 YAN PengFei， GUO AnRu， LIU HaiDong. Physical Testing and Chemical Analysis Part B： Chemical Analysis，  2018，  54（12）： 1435-1440

嚴鹏飞， 郭安儒， 刘海东. 理化检验化学分册， 2018，  54（12）： 1435-1440

7 XIAO LiuPing. Metallurgical Analysis，  2019，  39（3）： 74-78

肖刘萍. 冶金分析， 2019，  39（3）： 74-78

8 Dankowska A， Domagala A， Kowalewski W. Talanta，  2017，  172： 215-20

9 Zhou F， Li C， Zhu H， Li Y. Optik，  2019，  176： 512-517

10 Fedenko V S， Shemet S A， Landi M. J. Plant Physiol.，  2017，  212： 13-28

11 Lambert A， Asokan M， Issac G. J. Ind. Eng. Chem.，  2017，  51： 44-48

12 TAO Chen， LI ChunSheng， CHU WeiCheng. Chinese J. Anal. Chem.，  2019，  47（1）： 163-168

陶 琛， 李春生， 初威澄. 分析化学， 2019，  47（1）： 163-168

13 Tatikolov A S. Chem. Phys. Lett.，  2016，  665： 131-136

14 ZHU HongQiu， ZOU ShengNan， YANG ChunHua. Acta Optica Sinica，  2017，  37（6）： 331-338

朱红求， 邹胜男， 阳春华. 光学学报， 2017，  37（6）： 331-338

15 Martins A R， Talhavini M， Vieira M. Food Chem.，  2017，  229： 142-151

16 Hassan S A， Elzanfaly E S， Salem M Y， ElZeany B A. Spectrochim. Acta A，  2016，  153： 132-142

17 Zhang H， Ayoub R， Sundaram S. Automatica，  2017，  78： 202-210

18 Subramaman M， Sathappan S. Int. Arab. J. Inf .Techn.，  2015，  12（3）： 229-236

19 Zhao J， Netto M， Mili L. IEEE. T. Power Syst.，  2017，  32（4）： 3205-3216

20 Schillings C， Stuart A M. Siam. J. Numer. Anal.，  2017，  55（3）： 1264-1290

21 Luke R， Wouters J. IEEE. T. Neur. Sys. Reh.，  2017，  25（3）： 196-204

22 Mahboub V， Saadatseresht M， Ardalan A A. Stud. Geophys. Geod.，  2017，  61（1）： 19-34

23 Wei W， Shujie L， Haiyang Y U. J. Syst. Eng. Electron.，  2017，  39（7）： 1439-1444

24 Zhang X， Wang Y， Yang D. Energy，  2016，  115： 219-229

25 Strano S， Terzo M. Nonlinear Dynam.，  2016，  85（4）： 2353-2368

26 Xia B， Cui D， Sun Z. Energy，  2018，  153： 694-705

27 Lee B， Yun S， Lee H K. Int. J. Aeronaut. Space，  2016，  17（2）： 222-231