基于三菱PLC的AGV磁导航PID模糊控制与实现

赵 靖1， 李锻能， 王 冲

(1.桂林航天工业学院 广西航空物流研究中心， 广西 桂林 541004;2.广东工业大学 机电工程学院，广东 广州 510006)

AGV是工业自动化生产线中的关键设备，要求具备稳定实现生产过程搬运的能力，因此被广泛应用。近年来，传统PID控制技术已经不能适应AGV越来越高的控制跟踪要求。而模糊控制[1]、人工智能等智能控制方法，也已经不断地应用到AGV的控制技术研究中。但在实施模糊控制器应用时容易产生稳态误差，难以根据系统特性进行自适应调整。

国内有研究者[2]进行了基于PLC系统PID控制的仿真和实验分析，指出具备可行性。以磁条作为导航路径，三菱Fx-3U PLC作为控制核心，提出了一种基于位置RFID卡识别、PID模糊控制于一体的控制算法，试图解决差速式AGV在自动化生产线中路径的准确识别与快速跟踪精度不高的问题，并分析了编程过程中Modbus通信协议的理解难点。在后期在车间搭建硬件平台测试了AGV的稳定性。

1 AGV的模型建立

1.1 AGV的运行结构模型

所讨论的AGV为六轮差速式。前后轮为万向轮，中间2轮由2个伺服直流无刷电机直接驱动。小车沿着磁导航规划的路径行驶，车上装有磁敏传感器，其上有可以感应16位NPN型开关量的磁敏传感器，安装在磁轨道垂直距离约为10 cm，近小车前进端20 cm的位置。磁导轨附近放置RFID卡，卡上有8个状态寄存器标志位，可以记录小车位置、身份等信息，可为日后多小车多任务升级车间系统做准备。该车车身尺寸为1200 mm×667 mm×560 mm，最大载重为150 kg，要求行驶时路径偏差小于10 mm、停车误差不超过5 mm。

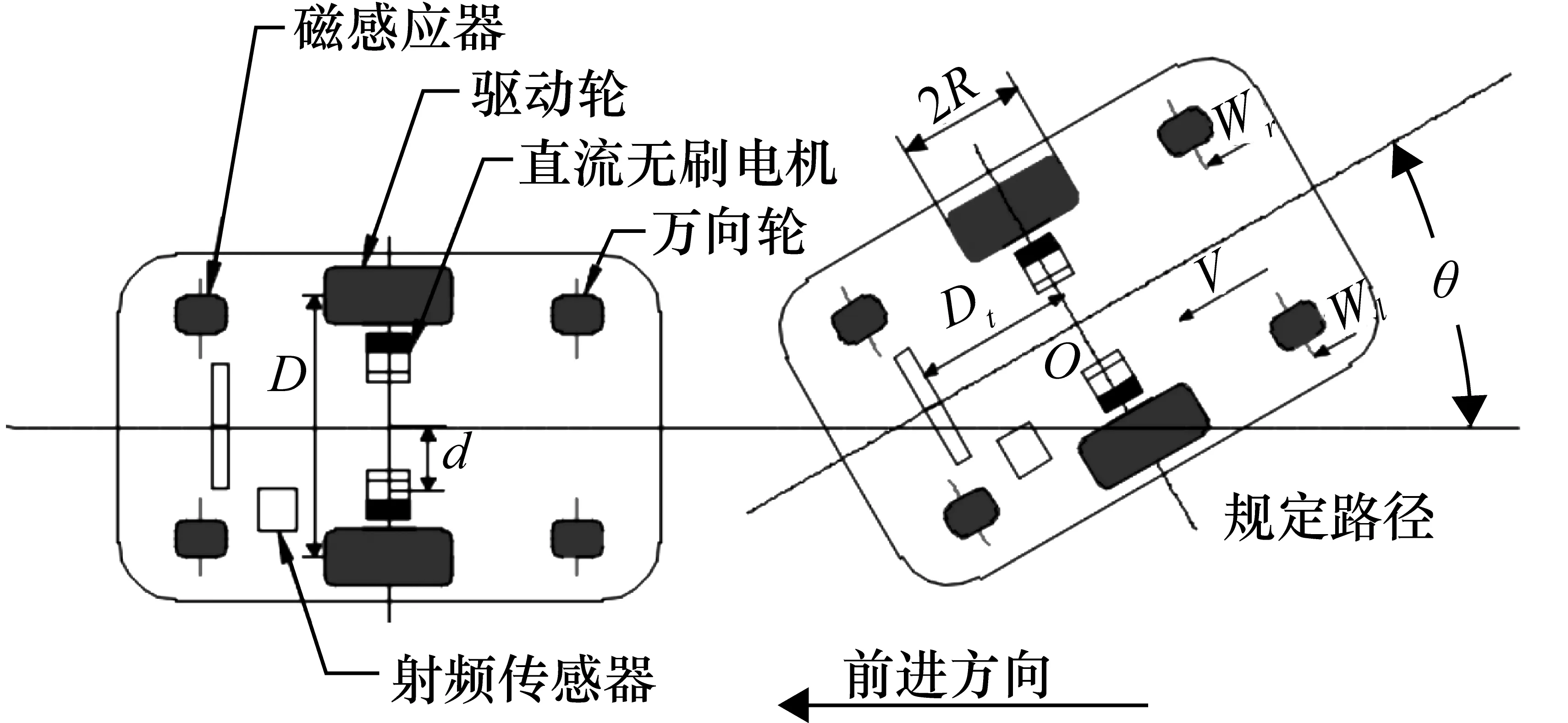
图1 AGV小车的运动学模型图

1.2 AGV的运动学模型及其状态方程

AGV运动学模型如图1所示，其中采用X坐标表示运行路径，O点是两驱动轮的中心。当左驱动轮转速以Wl表示，右驱动转速以Wr表示，不打滑情况下转速以W表示、θ为车体转角、R为驱动轮半径，D为2驱动轮的中心距、Dt为探头中心和2驱动轮中心连线的垂直距离，则运动学方程可通过以下步骤建立：

① 求解车体转动的角速度，见式(1)。

② 计算车体转动的角度，见式(2)，式中θ0为车体初始角度，下同。

③ 求车体O点的瞬时线速度，见式(3)。

④ 求探头中心点c的位置，见式(4)。

⑤ 求探头中心与轨迹中心点的差距，见式(5)。

⑥ 求处于圆弧段[设圆弧中心为(0，R)]的角速度，见式(6)。

⑦ 对上式两边求导，即可得出两偏差相对应的变化率，见式(7)。

⑧ 从而可知小车的空间状态方程，见式(8)。

⑨ 通过统计出系统的输入端以及输出端的大量数据，根据多目标的改进自适应遗传算法[3]，得到了系统数模型，其传递函数见式(9)。

⑩ 最终推导出整个系统的状态方程，见式(10)。

w=(Wl-Wr)×R/D

(1)

(2)

V0=(Wr+Wr)×R/2

(3)

(4)

(5)

w=(Wl-Wr)×R/D

(6)

(7)

(8)

(9)

(10)

2 基于PLC的模糊控制系统设计

2.1 参数自定义模糊PID控制器的设计

基于上述状态空间数学模型理论上可建立AGV的控制器算法。但数学模型的建立基于几点假设：摩擦力矩F(q,q)为零，未知外加扰动量为零。但AGV在生产车间系统中由于环境复杂，存在着滞后、非线性、时变、以及各种干扰等情况，导致控制的不确定性大。因此要满足生产线的控制要求需寻找更为合适的控制算法。模糊控制器是在常规控制器模型基础上升级设计的[4]，它能够从模糊控制表中读取PID参数，当输入量发生改变时，控制系统会通过解析模糊算法动态选择对应的模糊控制量来控制其输出参数。模糊PID控制器的设计原理是：将输入量分成几个区间，输入量经过模糊化处理后在映射到对应的模糊规则库的对应的PID参数上。这里设计模糊控制器所选择的输入量分为2个：AGV距离偏差e与角度偏差θ。设计该控制器时可以从磁导航上计算出这两个参数，而小车可通过感应标定的RFID卡刷新控制器中的PID参数，从而能在线调整PID参数，达到模糊控制目的。

2.2 有效磁条选择与应用

磁条感应点数是判断AGV位姿的重要参数，在AGV的模糊控制上有着一定的应用[5]。单个磁条点位读取如图2所示：每个磁条上共有16个点位的磁感应点，AGV正常直行时会检测到中间4个点位。转弯与刹车时点位各有差异。可通过磁条点上点位数计算出AGV的位置偏差e，进而推导出与预定轨迹的角度偏差角θ。磁导航一侧有8个点位，由于只有2个点位时表示直行，故累积点位初始值为10个点，设此时有N个点感应在磁条线上，经测试，AGV最大偏差为±15 mm，且感应点数与偏差距离呈线性关系。则位置偏差见式(11)，角度偏差见式(12)。

e=[(10-N·0.5)/8]×15

(11)

θ=arctan[e/Dt]

(12)

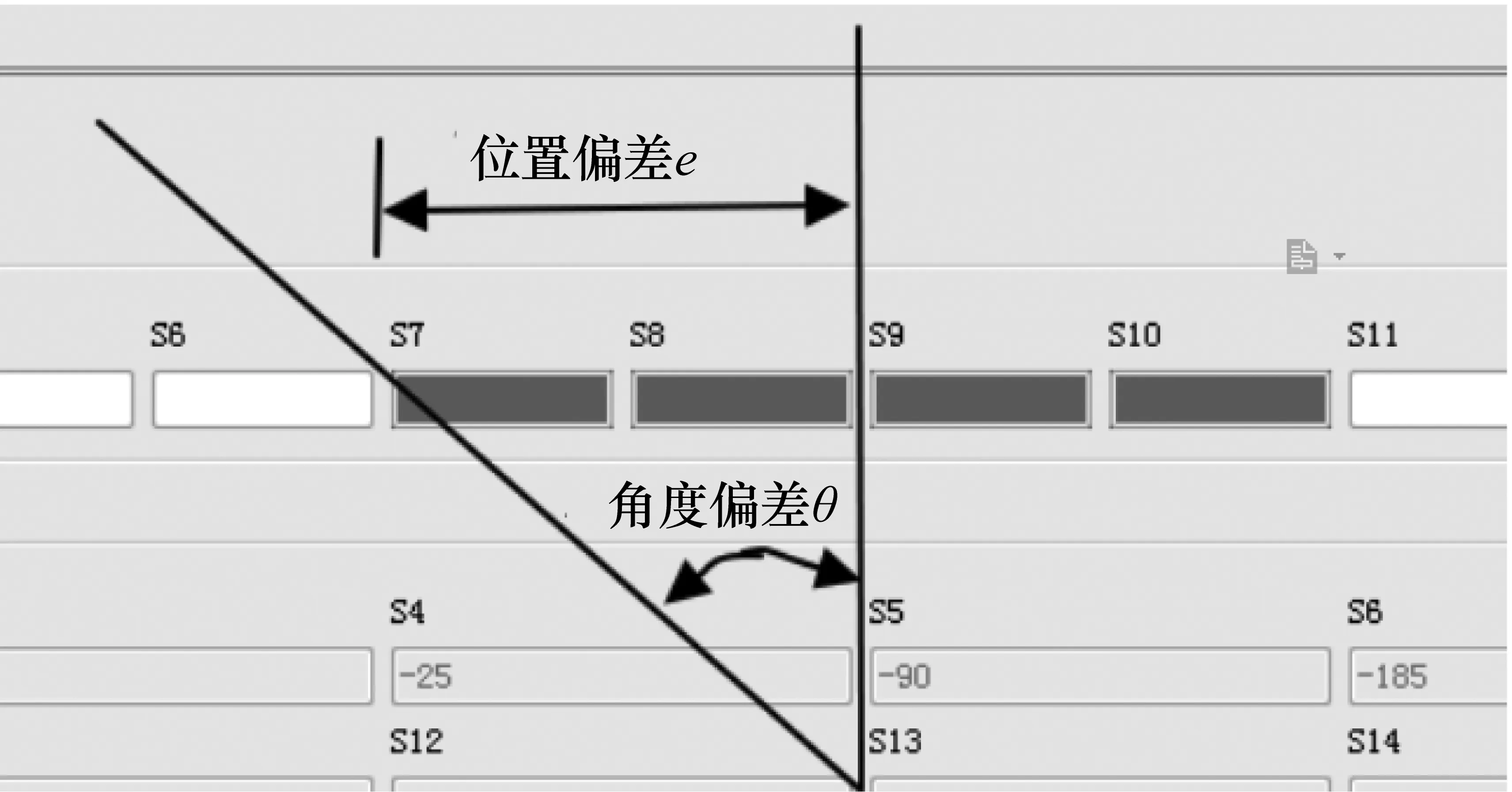
图2 磁条点位读取模型图

2.3 各段路径的跟踪识别

RFID卡作为路径标志寄存器，存储着小车的位置、状态等信息。而读取RFID卡的信息则需要通过PLC来完成，根据信息可以判断是否执行直行、转弯、加减速、装工件、卸工件等动作，还可以作为触发模糊控制器的开关，在车间物流配送系统中有着重要的应用[6]

2.4 Modbus通信协议的设计实现与测试

以三菱FX-3U系列为例，给出PLC与RFID卡的通信样本，其协议形式为Modbus协议。文献[7]提供了部分的Modbus指令模板，其指令有关的特殊辅助继电器和特殊数据寄存器M8411开始写通信格式。D8429设置主站通信模式。D8420设置从站响应时间。D8431设置延迟播放时间。D8432设置重复次数。设置好通信格式后，即可以将RFID卡中的数据读入到PLC中。RFID卡中共有8个状态寄存器。事先会由相应的写卡器烧录好数据。其测试过程如图3所示。使用PLC的烧写软件GX Works打开测试调试界面，当写有数据的点位被读取时界面上显示出蓝色。

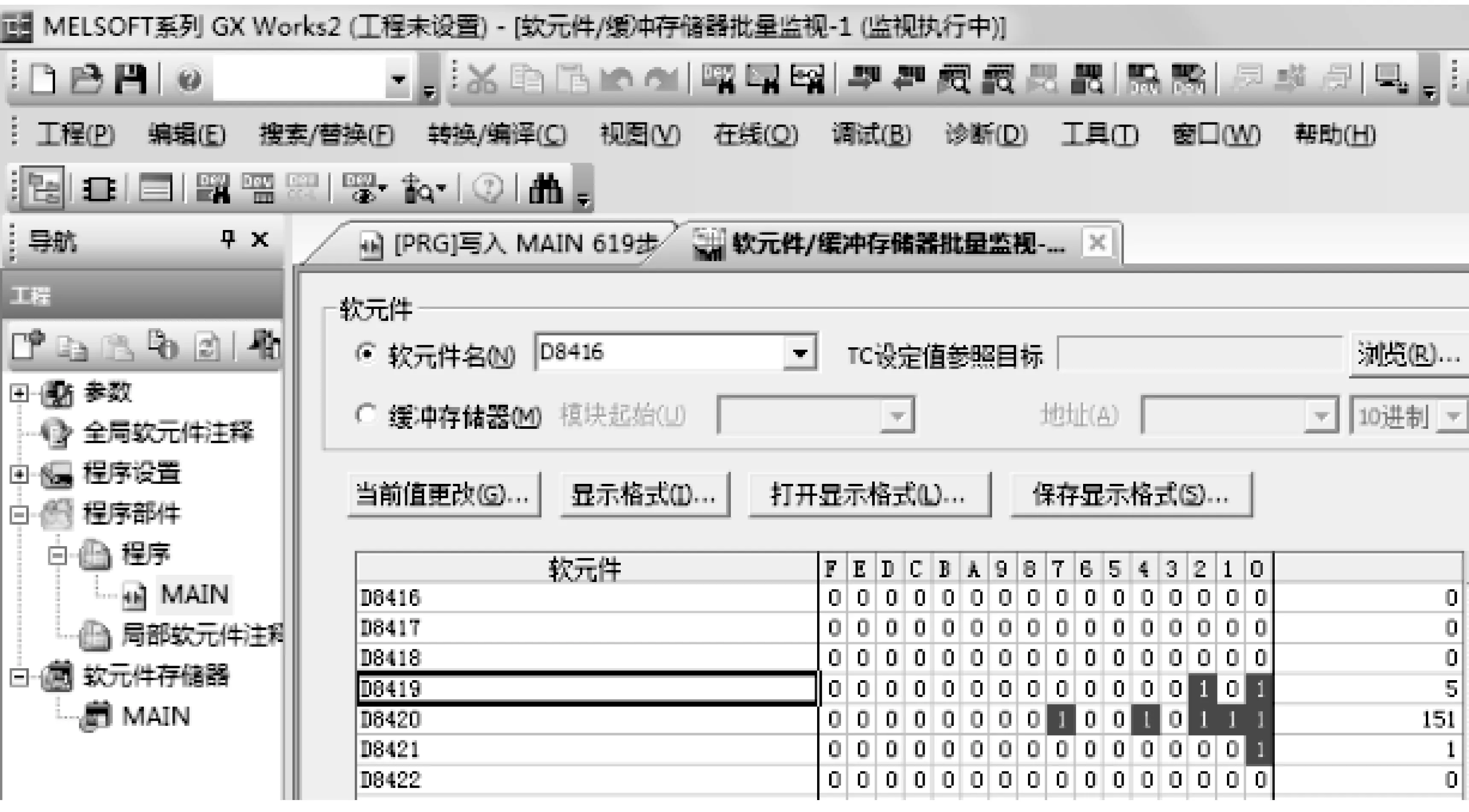
图3 RFID数据点测试示意图

2.5 模糊控制器的设计

2.5.1 定义输入语言变量

经过测试，确定小车的位置偏差e的基本范围是[±15 mm]。而角度偏差θ的基本范围为[±10°]。为匹配模糊论域，将距离偏差量化为{-15,15}。角度偏差取{-10°,10°}。隶属函数分布如图4所示：选取灵敏度高的三角函数{trimf}作为角度与位置偏差的隶属函数，从而定义位置偏差e的论域，见式(13)。其中LF表示小车在目标路径的左边较远处，LN则表示左边较近，MD则表示在路径中间，可以不调节，LR则同理。同理定义角度偏差θ的论域见式(14)。

E∈{LF(LeftFar),LM(LeftMiddle),LN(LeftNear),MD(Middle),

RN(RightNear),RM(RightMiddle)，RF(RightFar)}

(13)

θ∈{LFθ(LeftFar),LMθ(LeftMiddle),LNθ(LeftNear),MDθ(Middle),

RNθ(RightNear),RMθ(RightMiddle)，RFθ(RightFar)}

(14)

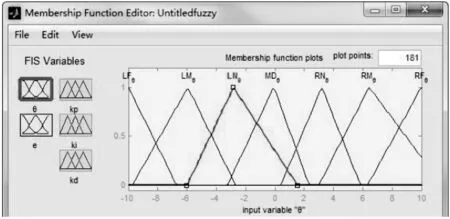
图4 距离偏差e函数隶属分布图

2.5.2 定义输出语言变量

定义3个输出语言变量：kp为比例系数,ki为积分调节系数,kd为微分调节系数。分别建立对应的语言值，见式(15)。

(15)

2.5.3 规则表建立

根据驾车经验，当小车位置偏离目标位置较大时，应快速调整方向盘回正路径，此时应加大比例环节，而当小车反复在目标路径振荡时，则可以增大积分环节。模糊控制器有2个输入变量e与θ，以及3个输出变量kp、ki、kd。如图5所示。依据小车的反馈信息，参照距离偏差e与角度偏差θ，制定出适应于AGV的40条模糊纠偏规则，并建立语言变量赋值表达式，如图5所示。

在Matlab建立模糊规则控制器后，可以查看到模糊规则曲面图，如图6所示：可见输出变量的变化较为平滑，从而系统的稳定性也更强。

2.5.4 输出量的清晰化

为了控制参数的需要，还需要通过模糊规则推理得出的模糊量并经过非模糊化处理才能得出控制参数。一般有面积中心法、面积等分法、极大平均法。

本文模糊清晰化方式采用面积中心法[8]，利用面积比计算出隶属度的权重比，计算公式为

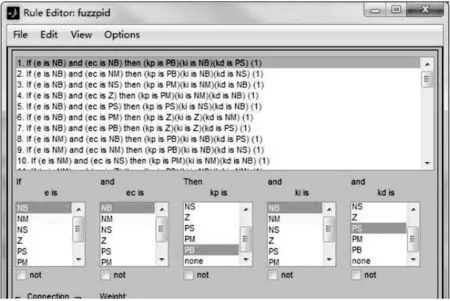
图5 距离偏差e与角度偏差θ模糊规则表

对应的PID参数此前已写成模糊控制表，提供在线查询功能修改PID参数功能。

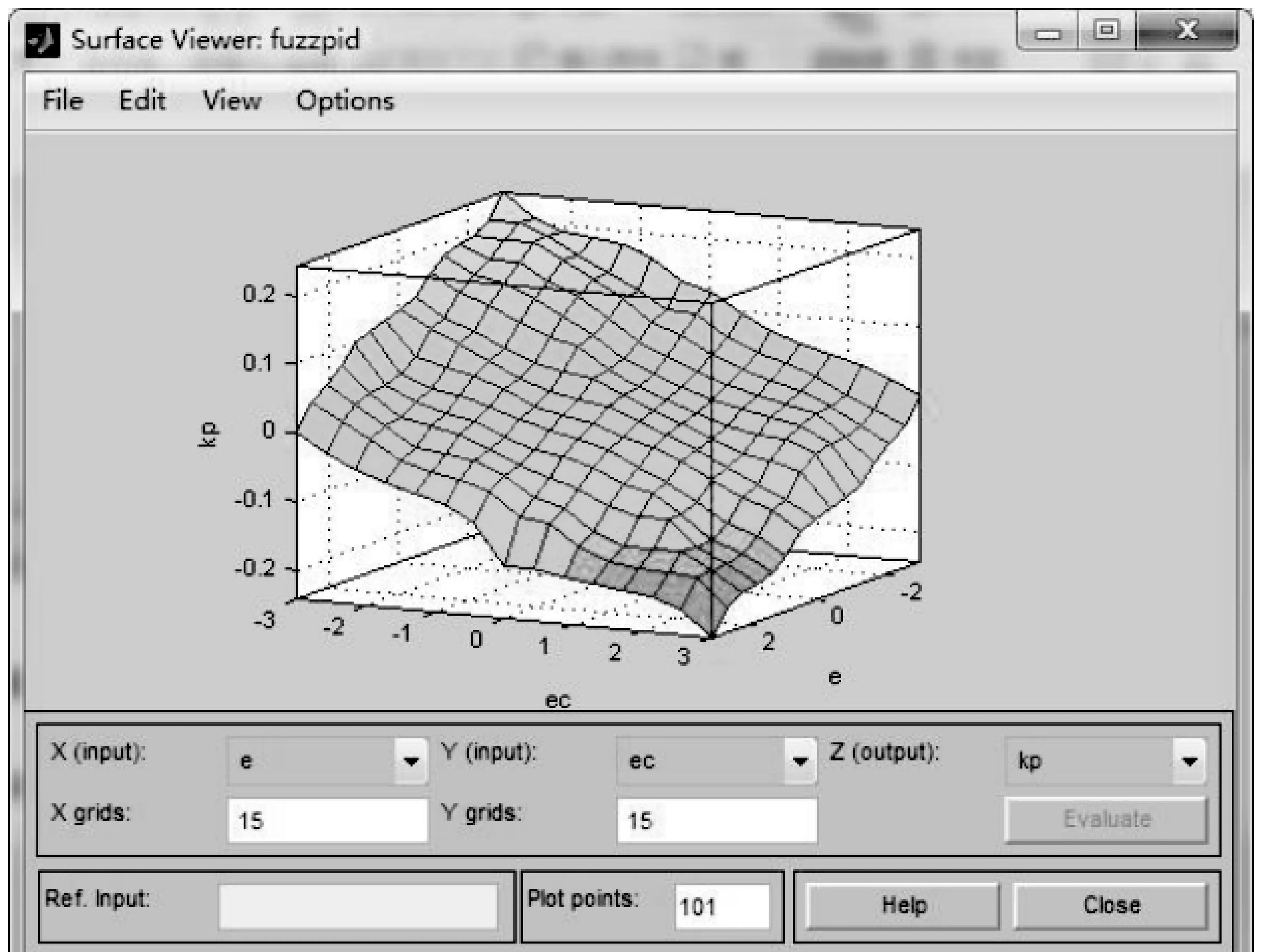
图6 模糊规则曲面图

3 控制算法仿真及分析

为验证模糊PID模糊控制器的有效性和优越性，对采用普通PID控制和模糊PID模糊控制的控制效果进行了Matlab仿真对比测试，如图7所示，为模糊PID控制系统，普通PID控制在此不赘叙。

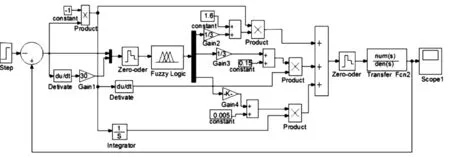
图7 模糊PID控制Matlab仿真图

仿真时设置小车的初始角度偏差为6°，初始位置0 m，目标距离分为两端，前段3 m测试直线轨迹，3 m后测试转弯轨迹。分别得到图8所示的车轮转速相应偏差对比图和图9所示的位置偏差的响应曲线对比图。

图8仿真结果表明，在有干扰信号下AGV的运行轨迹在1 s左右都能调整位姿，而模糊控制曲线调整时车轮过渡更平顺，而从图9偏移位置情况看，模糊控制的路径跟踪能力明显优于普通PID路径跟踪能力。可调整到磁条预定轨迹并能稳定运行，能够看出该控制器系统超调量极小，且响应速度较快。

4 车间实车巡航测试实验

为了测试模糊PID控制器在AGV小车上的性能，检验仿真结果、结构布局和软件设计的合理性，结合设计数据搭建了AGV硬件测试平台，分别铺设了直线磁轨道和环形磁轨道进行测试，测试的路径示意图如图10所示，硬件系统包括AGV小车、接驳台、上下料机器人以及机床。

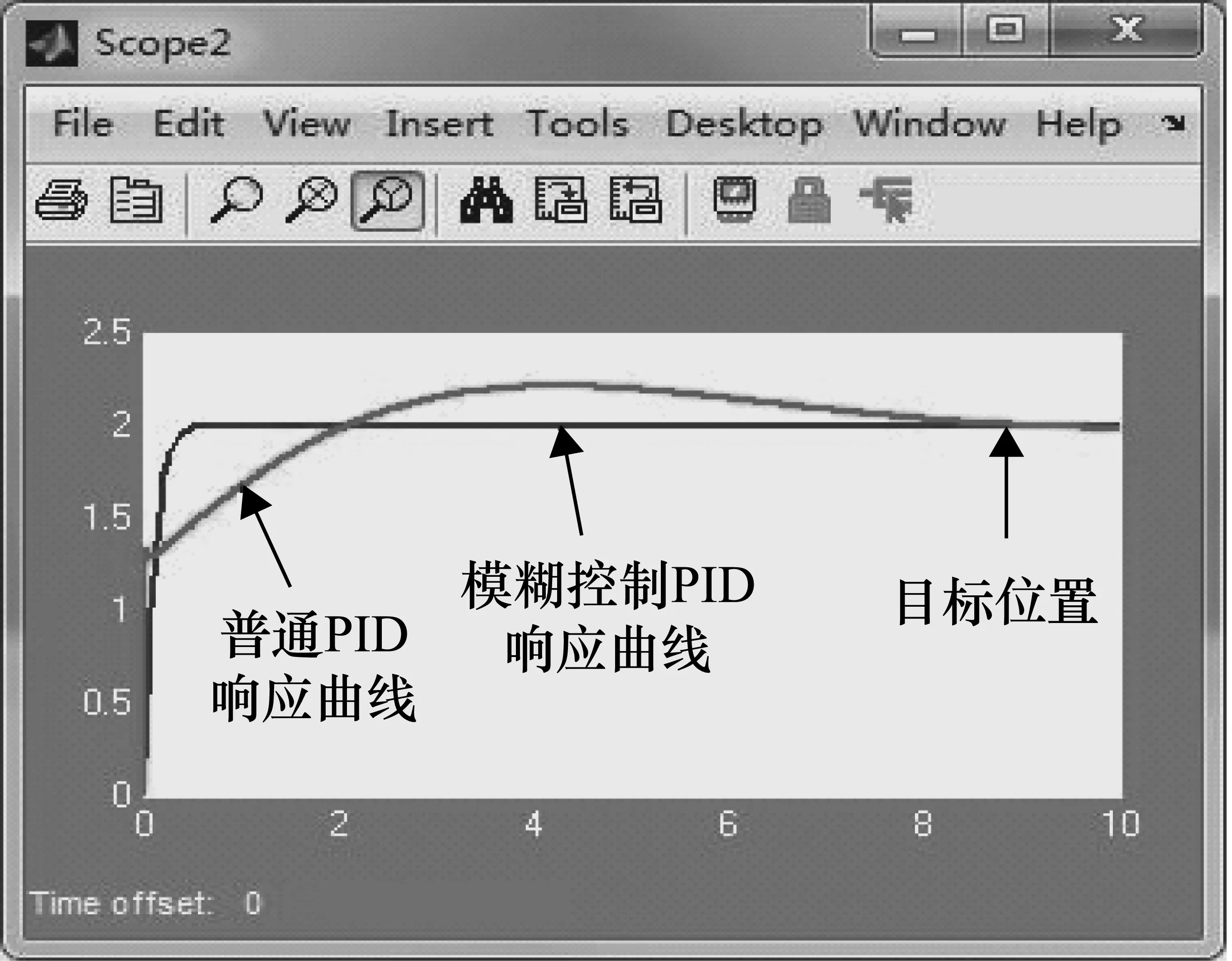
图9 位置偏差响应对比图

实测仍用Matlab仿真测试数据，实测结果表明，AGV小车能沿着铺设的磁条稳定直行和转弯，车速在40 s左右趋于稳定，而普通单一PID控制器车速在77 s左右出现超调量，并在90 s左右出现最大超调量。转弯时稳定性则表现更优，停车时刹车更精准。在模糊PID控制器系统下反应更灵敏，循迹速度更快。能在指定的工位稳定停车执行工件装卸等动作，偏差的变化过程也与实际的纠偏过程吻合，表明基于PLC的模糊PID控制器的跟踪性能稳定且更准确。

5 结束语

模糊PID控制具有多步结合预测、滚动优化、反馈校正等特点[9],其所采用的控制策略,扩大了系统动态行为的信息利用率,提高了系统运行的稳定性,具有其他控制方法所不具有的先预测、再校正、后控制的优点。作为输入的模型可以根据AGV信息的不同来设定，灵活性高，操纵性好。

实验测试表明，基于三菱FX-3U的模糊PID控制器的跟踪性能稳定准确，完全能够满足该3C自动化生产线的要求。