WSNs中基于RSSI优化的节点定位算法研究

(淮阴工学院 自动化学院,江苏 淮安 223003)

无线传感网络 (Wireless Sensor Networks，WSNs)[1-2]是由大量的微型、具有通信能力的传感节点组成。目前，WSNs已广泛应用于健康医疗服务、环境监测等应用，而估计传感节点的位置是WSNs应用的基础。

目前，根据定位机制的不同，可将定位算法划分为与距离无关(Range-Free)和距离相关(Range-Based)的定位算法。前者是依据网络的连通性估计未知节点位置，如最短路径 (Shortest Path,SP)定位算法、质心定位算法、跳距矢量(Distance Vector-Hop,DV-Hop)算法等[3]。而后者是先依据测量的距离或角度信息，然后再结合最小二乘、三边测量法等计算未知节点的位置。经典的测距算法有：基于到达时间(Time of Arrival,TOA)[4]、基于接收信号强度指标RSSI[5]、基于到达角度[6]、基于到达时间差(Different Time of Arrival,TDOA)[7]。

由于RSSI测距无需额外硬件设备，被广泛应用于低成本、低开销的无线传感网络，成为室内定位研究的热点。然而，基于RSSI测距算法普通存在较大的测距误差。原因在于：无线信号容易受到传输环境的影响。为此，研究人员提出了不同的对RSSI值进行修正的算法。例如，文献[8]利用高斯分布优化RSSI值。而文献[9]引用粒子滤波算法优化测距，但也增加了一定的运算量。此外，文献[9]和文献[10]分别引用加权均值、卡尔曼滤波优化RSSI值。

为此，基于RSSI改进的混合蛙跳的定位算法(Modifying RSSI Ranging-Based Shuffled Frog Leaping Localization Algorithm,MRSSI-SFL)。MRSSI-SFL算法先多次测量同一点的RSSI值，再利用正态分布优化RSSI值。然后，利用加权质心定位算法估计未知节点位置，并据此位置设置搜索区域，最后利用混合蛙跳算法优化未知节点的位置。实验数据表明，提出的MRSSI-SFL定位算法可有效降低定位误差。

1 RSSI测距原理

由于成本低，RSSI测距被广泛应用。RSSI测距利用所接收的无线信号强度的衰减来估计收/发间的距离。然而，无线信道存在较多的不稳定因素以及多径效应，导致信号强度的衰减与距离的关系存在波动。针对此情况，选择基于对数-常态分布的自由空间损耗模型作为无线信号传播模型。

首先，建立自由空间损耗模型：

PL(d0)=32.44+10nlgd0+10nlgf

(1)

式中，d0、n分别为传播距离、传输路径衰减因子；f为信号频率。

而对数-常态分布模型可表述为

PL(d)=PL(d0)+10nlg(d/d0)+ζn

(2)

式中，PL(d)为传输距离d时的路径损耗，而PL(d0)为当d0=1 m时的路径损耗；ζn为零均值的高斯变量函数。

结合式(1)和式(2)，从相离距离为d的节点所接收的信号RSSI:

RSSI=Psend+Pamplify-PL(d)

(3)

式中，Psend、Pamplify分别为发射功率、天线增益。

2 MRSSI-SFL

所提出的MRSSI-LM定位算法先多次测量RSSI值，并利用正态分布函数优化的RSSI值进行测距。随后，利用加权质心算法设定搜索区域，最后利用混合蛙跳迭代算法优化未知节点位置。整个定位过程如图1所示。

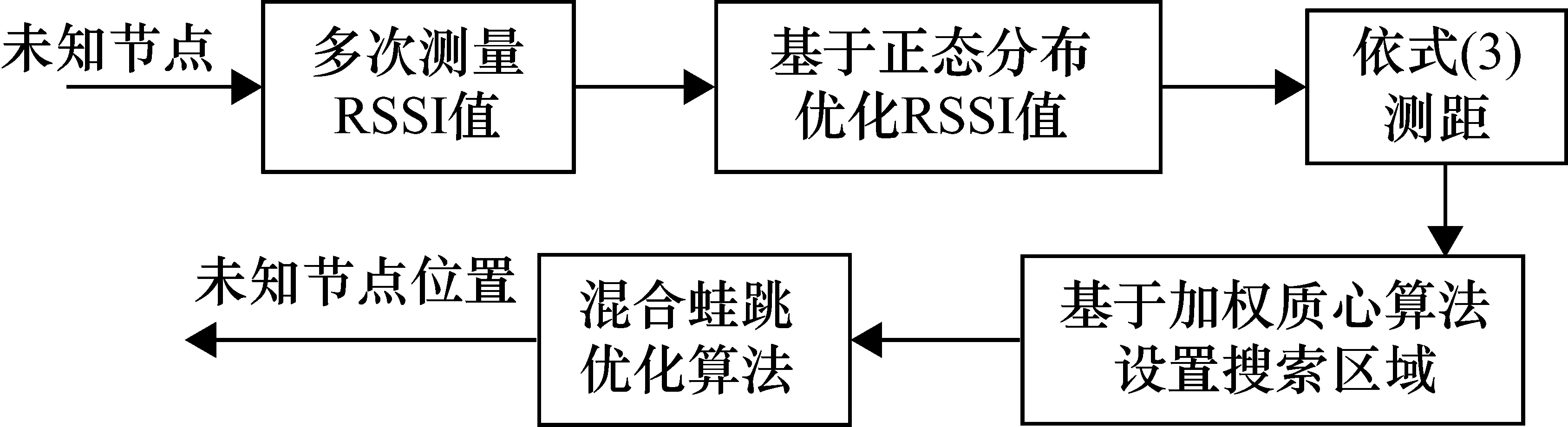
图1 定位框图

2.1 基于正态分布测距

由于无线环境具有多变特性，仅利用单一测量的RSSI值估算距离存在较大误差。为此，需要多测量同一个发射点的RSSI值。MRSSI-SFL算法对同一个地点多次测量，然后利用正态分布计算阈值。假定RSSI1，RSSI2，…，RSSIm表示RSSI的总体样本，相应地，rssi1，rssi2，…，rssim表示对应的样本观测值。据此，可建立似然函数:

(4)

式中，μ、σ2分别为均值、方差。

对式(4)两边取μ、σ2偏导数，可得方程组：

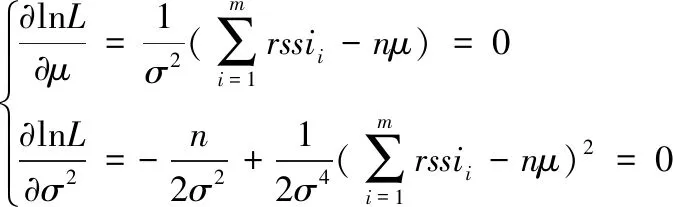
(5)

通过求解式(5)可得μ、σ2的最大似然估计值为

(6)

通过上述过程，便能得到正态分布的均值和方差。最后将RSSI代入式(3)就能实现测距。

2.2 基于质心加权的初始解

通过2.1节获取距离信息后，再选择离未知节点最近的3个锚节点。然后，以未知节点到3个锚节点的距离为半径，以锚节点坐标为圆心画3个圆。3个圆的重叠部分表示未知节点可能在的区域，如图2所示。

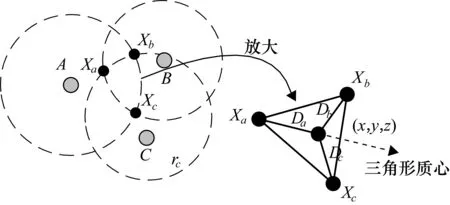
图2 加权质心算法示意图

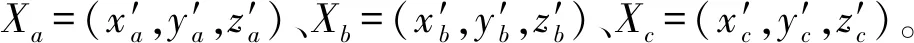
(7)

式中，ωa=1/(Db+Dc)、ωb=1/(Da+Dc)、ωc=1/(Db+Da)为3个交点的权重。以(x,y,z)为中心，以h为搜索空间的内切球半径构成搜索空间：

(8)

为了提高了定位精度，利用(x,y,z)建立青蛙种群的活动区域，即搜索空间。

2.3 基于混合蛙跳的位置优化

混合蛙跳算法是通过仿效青蛙种群搜索食物的过程，进而完成寻优。此过程包括种群信息交换、子群内部交流。混合蛙跳算法实现步骤如下[12]。

(1) 建立初始种群，种群中候选解个数为P。

(2) 设置适应度函数，并将P只青蛙按适应值进行排序，且从小至大排列。

适应度函数的定义为

(9)

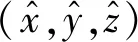
(10)

式中，di为测量距离；k表示与未知节点连通的锚节点个数。

式(9)中的f(x,y,z)表示误差之和，误差越小，定位越准确，其定义为

(11)

(3) 分组。将种群依据交替原则划分为m个子群。

(4) 子群搜索。按顺序搜索每个子群，直到满足子群内的搜索次数。搜索过程如下：

① 先确定最差、最好的青蛙。假定Xb、Xw表示所有子群中最好的青蛙、最差的青蛙。而Xg表示种群的最好青蛙。

② 对最差的青蛙Xw进行更新：

D=C×rand()×(Xg-Xw)+(1-C)×rand()×(Xb-Xw)

(12)

newXw=oldXw+D,Dmin≤D≤Dmax

(13)

式中，C为权重系数，初值为1，并不断更新，如式(14)所示：

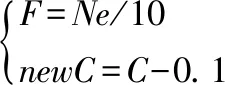
(14)

其中Ne、F为子群搜索次数、子群每搜索次数。

③ 用种群最好的青蛙Xg替换Xb，随后，重新计算式(12)～式(14)。

(5) 混合子群。完成了m个子群优化后，就回到步骤②，重新排序。

(6) 检测是否满足迭代次数K,否则就返回步骤(3)。

整个定位流程如图3所示。首先参数初始化，包括候选解个数P、子群个数m、全局信息交换次数为K、子群内搜索次数Ne。然后，测量RSSI，并进行优化，再进行测距，并利用加权质心算法估计未知节点的位置，再设置搜索区域。随后，构建初始种群，再计算每种群的适应度函数。然后，依据混合蛙跳优化未知节点的位置。

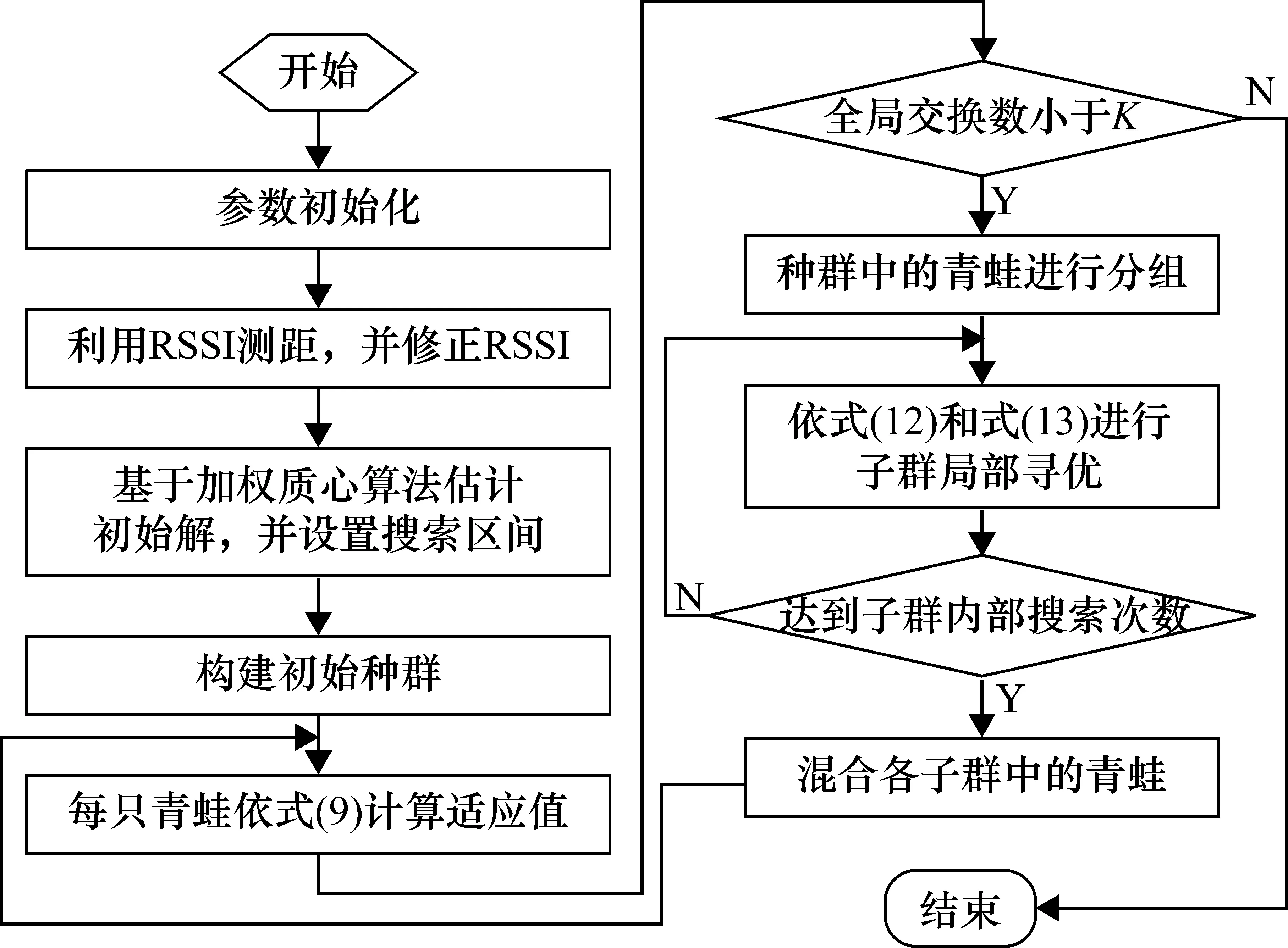
图3 算法流程图

3 仿真实验及分析

为了更好地分析MRSSI-LM算法的定位性能，利用Matlab建立仿真平台。考虑1000 m×1000 m×1000 m的正方体区域，且在此区域内随机部署N=300个传感节点，其中锚节点比例为ρ。即锚节点数Manchors=N×ρ,且0<ρ<1。节点通信半径R=100 m。此外，青蛙子群数为50个，且每个子群内的青蛙数为35只。子群内部搜索次数Ne=50、全局交换信息的次数K=100。

为了更好地分析MRSSI-SFL的定位性能，选择基于RSSI的加权质心定位算法(RSSI+加权质心)作为参照，并进行性能比较，包括定位误差率和定位覆盖率。定位误差率定义为

(15)

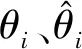
3.1 实验1

本次实验分析节点总数对定位误差率的影响，其中ρ=0.3。每次实验独立重复10次，取平均值作为实验数据，如图4所示。

从图4可知，定位误差随节点总数的增加而呈下降趋势，但存在一定的波动。相比于RSSI+加权质心算法，提出的MRSSI-SFL算法的精度得到有效提高。当节点数较大时，定位误差率下降了6%；而当节点数较小时，定位误差率下降至2%。原因在于：MRSSI-SFL算法通过优化RSSI值，提高了测距精度，同时利用混合蛙跳算法优化了定位精度。此外，节点数的增加有利于测距信息的提高，进而降低了定位误差。

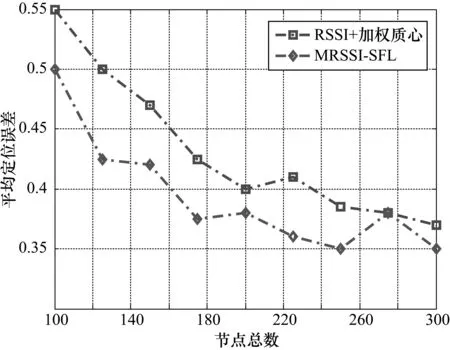
图4 定位误差率

3.2 实验2

本次实验分析锚节点数对平均定位误差的影响。节点总数300，锚节点数从30增加到150，实验数据如图5所示。

从图5可知，锚节点数的增加降低了平均定位误差。原因在于：锚节点数越多，获取的测距信息越准确，这有利于定位精度的提高。与RSSI+加权质心算法相比，提出的MRSSI-SFL算法的平均定位误差得到有效控制，并且随锚节点数的增加而提高。例如，当锚节点数达到150时，MRSSI-SFL算法的平均定位误差比RSSI+加权质心算法下降近9%。

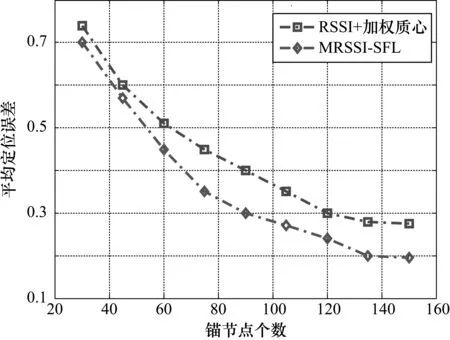
图5 锚节点数对平均定位误差的影响

3.3 实验3

最后，建立实验分析锚节点数对MRSSI-SFL算法的覆盖率的影响，其中节点总数为300，R=100 m、锚节点数从30增加到150变化，每次实验独立重复10次，取平均值作为最终的实验数据，如图6所示。

从图6可知，锚节点数的增加有利于定位覆盖率的提高，当锚节点数达到150时，RSSI+加权质心和MRSSI-SFL算法的定位覆盖率均达到0.9。在锚节点数整个变化区间，MRSSI-SFL算法的定位覆盖率略高于RSSI+加权质心。这也说明，MRSSI-SFL定位算法在估计未知节点位置时，对锚节点的分布要求较低。

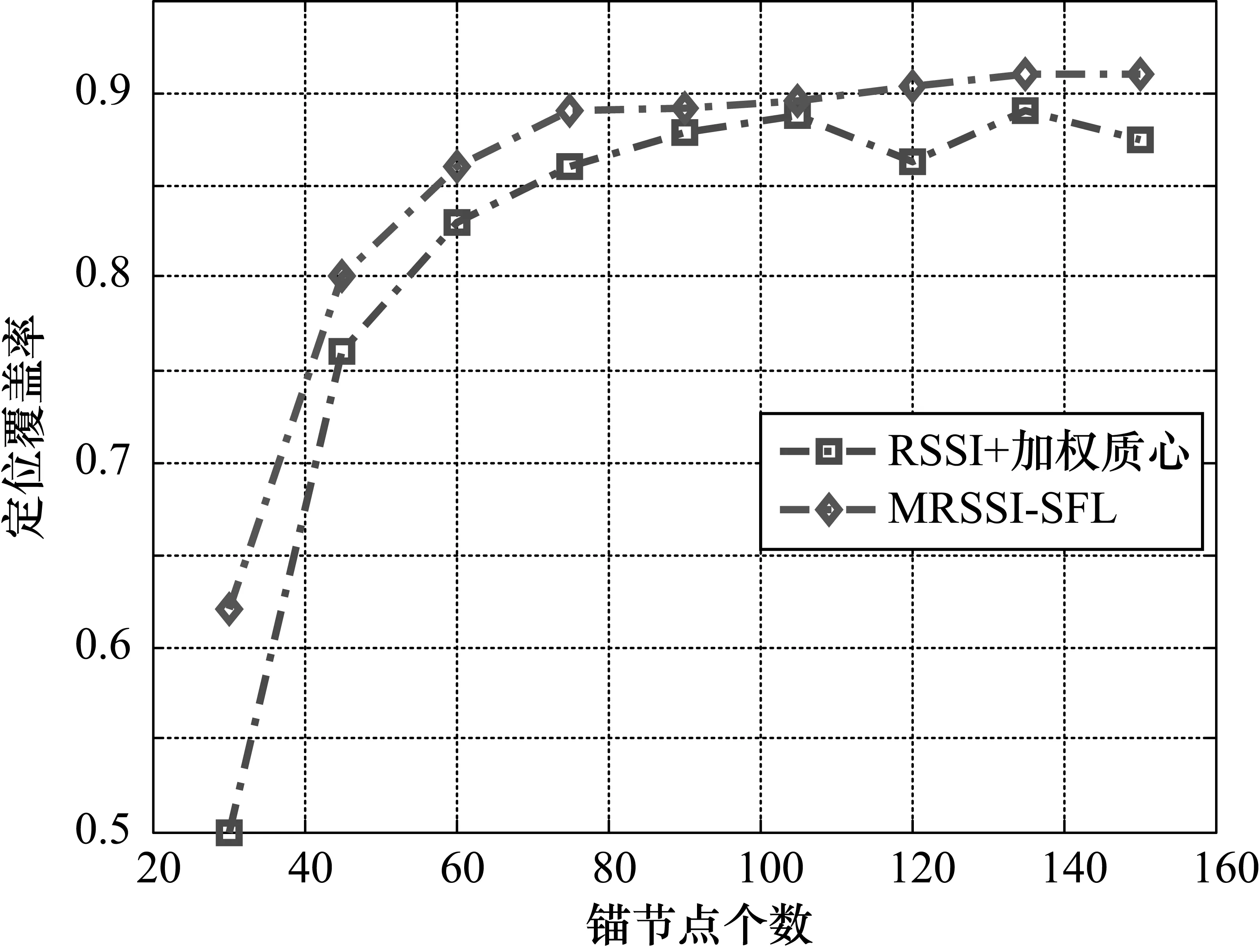
图6 锚节点数对定位覆盖率的的影响

3.4 实验4

本小节用运行时间数据分析算法的复杂度，如表1所示。从表1可知，提出的MRSSI+SFL算法的运行时间略高于RSSI+加权质心算法，约0.07 s。这说明，MRSSI+SFL算法在提高定位精度的同时，并没有加大算法的复杂度。

表1 算法的运行时间

4 结束语

针对WSNs的传感节点问题，提出基于RSSI改进的混合蛙跳的定位算法(MRSSI-SFL)。MRSSI-SFL先优化RSSI值，提高测距数度。然后，再利用加权质心定位算法估计未知节点位置，并将此位置作为蛙跳算法迭代的初始值，通过迭代，提高未知节点位置的精度。实验数据表明，提出的MRSSI-SFL算法相比RSSI+加权质心算法，其定位精度得到有效提高，也提高了定位覆盖率。后期，将进一步优化定位算法，降低算法的复杂度。