基于运动预测的车辆横向稳定性控制

陈亚伟,邵毅明，郝西祥，甘元艺

(重庆交通大学 a.机电与车辆工程学院； b.交通运输学院， 重庆 400074)

近年来，针对车辆横向稳定性控制的研究日益增多[1-9]。在众多研究中，文献[3]采用基于质心侧偏角的控制阀值来进行车辆的横向稳定控制，能够改善车辆的稳定性能。文献[4]提出了通过估计车辆的质心侧偏角，结合最优控制理论来提高车辆稳定性的方法。文献[5-7]研究了车辆的制动控制策略对车辆稳定性的影响，采用差分制动的方法来改善车辆在摩擦极限工况下的稳定性。上述文献所提出的控制方法虽然可以保证车辆横向控制的精度要求，但是由于系统的延迟和滞后，很有可能使车辆的横向状态失去稳定性。

针对传统方法的不足，文献[8]提出了基于预测的车辆横向稳定性控制方案，通过预测横摆角速度跟踪车辆期望横摆角速度，从而降低控制系统对车辆横向稳定性控制的迟滞效应。文献[9]设计了一种MPC横向稳定控制系统，采用前轮转向和差分制动作为输入，并通过实车实验验证了该种方法的有效性。在实际问题中，MPC方法是基于在线优化的，由于计算量大、迭代速度慢等缺陷，导致控制的实时性很难保证。综上所述，虽然车辆的横向稳定性控制日益得到重视，但目前还有一些问题亟待解决。如何基于车辆的横向动力学特性实现其控制的稳定性，并兼顾精度要求，还有待进一步探讨。

本文提出了一种基于车辆运动预测的横向稳定控制系统，通过对未来转向输入的预测和非线性车辆模型的数值积分，车辆运动预测器可以确定控制起始时序。基于运动预测，由横向状态空间方程得出未来期望的轮胎侧偏角，轮胎侧偏角控制器通过跟踪该期望值使车辆保持稳定状态。

由于本文提出的控制系统在非线性车辆模型的基础上通过精确的运动预测可以将轮胎侧偏角限制在峰值下，因而能够提高横向稳定性。与基于当前状态的控制算法相比，该算法在各种仿真工况下都能以较小的制动力来稳定车辆。

1 基于运动预测的控制策略

稳定性控制系统的主要目标是通过运动预测使车辆在极限操纵状态下能够保持稳定状态。当轮胎侧偏角处于小角度时，轮胎的侧偏特性具有线性特征并且有可预测性，但当侧偏角超过其峰值时，轮胎侧偏特性显示出非线性特征。由此可见，要实现车辆的稳定性控制，可以通过限制前后轮胎的侧偏角使其处于线性区范围内。

如图1所示，通过预测短时域(0.2 s)内车辆的状态，并在轮胎侧偏特性进入非线性区之前控制轮胎侧偏角，使其处于极限值之下，以保证轮胎侧偏角不进入非线性区，从而实现在减小制动力的同时提高车辆的稳定性。

图1 系统控制目标

如图2所示，整个稳定性控制系统由2个连续的部分组成。首先，在运动预测与规划部分，通过非线性车辆模型预测车辆未来的转向输入，根据预测的结果来判定控制是否执行；然后，计算使车辆保持横向稳定的期望轮胎侧偏角；最后，通过轮胎侧偏角控制器控制轮胎的侧偏角跟踪期望值，外部控制器计算得到每个轮胎的制动压力输入。

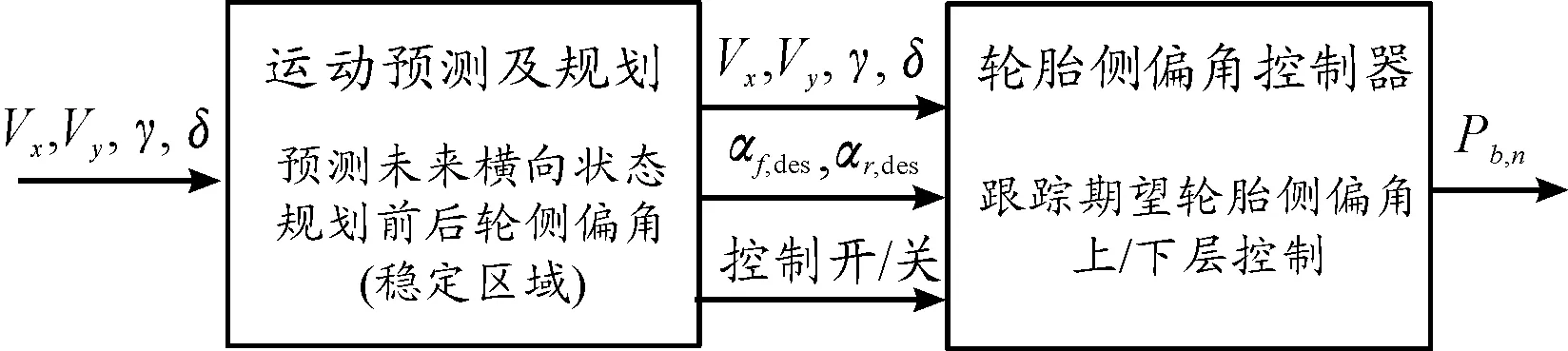
图2 控制算法的架构

2 车辆模型

为了预测车辆的未来横向运动，本文采用单轨模型表示车辆的横向动力学。由于需要描述轮胎侧偏角与横向力之间的关系，故基于魔术轮胎公式建立了非线性轮胎模型[10]。

2.1 基于侧偏角的单轨模型

如图3所示，车辆的侧向速度、横摆角速度和转向角决定了侧向动力学特性。假设侧偏角足够小，则有横向动力学方程[11-12]：

(1)

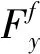
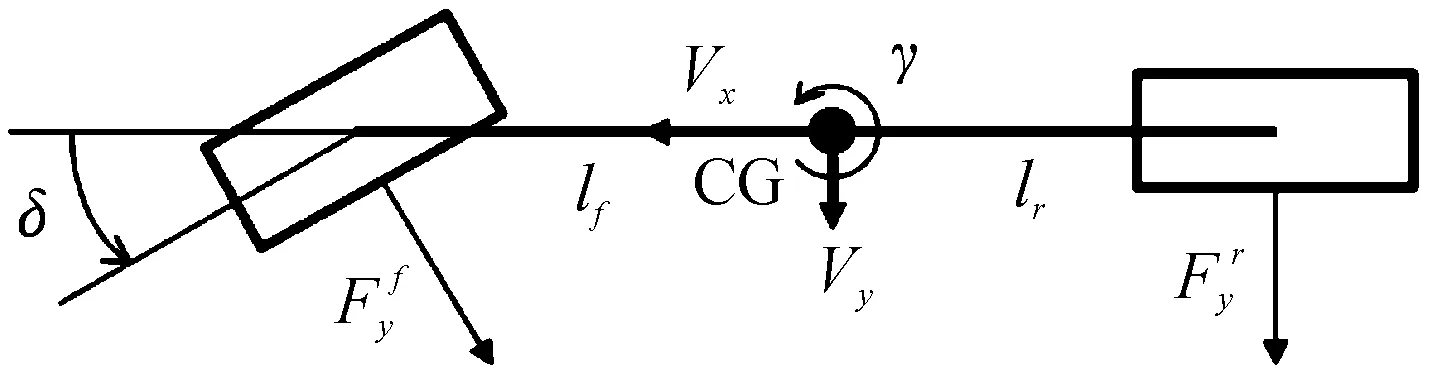
图3 车辆动力学模型

由图3可知，前后轮胎的侧偏角表示为：

(2)

联立式(1)和(2)，车辆的横向动力学可表示为：

(3)

(4)

2.2 魔术公式轮胎模型

在预测车辆的未来运动时，采用魔术公式轮胎模型来描述轮胎的非线性特征，轮胎的横向力表示为

Fy(α)=Dsin{Carctan[Bα-E(Bα-arctan(Bα))]}

(5)

其中:α是轮胎的侧偏角;Fy表示轮胎的横向力;B、C、D和E分别表示轮胎的刚度因子、曲线形状因子、曲线峰值因子和曲线曲率因子。

在本文中，为了更加准确地预测车辆的未来运动，考虑了轮胎法向力对横向力的影响。由于在一定范围内，横向力随着轮胎垂直力的增加而增加，所以魔术公式轮胎模型中的参数D可以为摩擦因数，将式(5)改写为

Fy(α，Fz)=DFzsin{Carctan[Bα-E(Bα-arctan(Bα))]}

(6)

2.3 直接横摆力矩控制的执行机构模型

如图4所示，为了描述通过差分制动产生的横摆力矩，需要建立车辆的执行机构动力学模型。

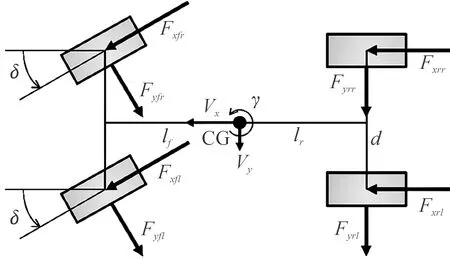
图4 执行机构模型

直接横摆力矩控制系统的输入矢量可以表示为：

x=[Vx,Vy,γ]T

uc=[Fxfl,Fxfr,Fxrl,Fxrr]T

(7)

状态方程如下：

(8)

其中:Fxfl、Fxfr、Fxrl、Fxrr分别表示前左、前右、后左、后右轮胎的纵向力;Fzf、Fzr分别表示前、后轮胎的垂直力;d表示车辆的轮距。

3 运动预测与规划算法

预测车辆的未来运动需要车辆模型参数、初始状态和未来输入。利用这些信息，通过对车辆模型的数值积分，可以求得车辆的未来横向状态。

3.1 未来转向预测

车辆的未来转向输入可以通过推导一个2阶多项式过去的转向输入随时间的变化来预测。转向角预测方法如图5所示，采用最小二乘法寻找最优2阶多项式进行预测。对于最小二乘法，使用与预测层相同时间(0.2 s)的转向数据。

图5 未来转向预测方法

由于车辆在实际行驶中，其未来转向输入是未知的，但通过最小二乘原理，可以求得该未来转向输入的最佳估计值，再通过对观测值按照最小二乘准则进行平差，可以使观测值的修正值满足一定的约束条件，因而可在一定程度上提高车辆未来转向输入的预测精度。

3.2 车辆模型的数值积分

欧拉法是求解给定初值的常微分方程的1阶数值方法，可用于数值积分，表示为：

(9)

式中:x表示状态空间;h表示采样时间;f(ti,x(ti))表示x(ti)的导数。

在车辆的运动预测中，可以通过预测未来转向角和车辆非线性模型计算出每一采样时间的车辆状态导数。显然，当预测范围过长时，预测状态与实际值的偏差将逐渐增大，如果预测范围太短，就无法通过提前预先设定的方法提高控制器的性能。综合各因素，本文选择0.2 s的预测时间来平衡预测精度和控制器性能之间的冲突，同时设定数值积分的采样时间与控制器的采样时间一致，为10 ms。

3.3 参考前后轮胎侧偏角规划

为了保证车辆的稳定性，在计算未来的轮胎侧偏角参考值时，该参考值应该处于线性区，同时与驾驶员预期的横摆运动保持一致。由于运动预测器基于非线性轮胎模型预测车辆的未来横向状态，为了保证车辆的稳定性，如下计算每个步骤期望的轮胎侧偏角：

(10)

其中:αf,des(k+1)、αr,des(k+1)分别表示第k+1步期望的前后轮胎侧偏角;δ(k+1)、γ(k+1)分别表示第k+1步的预测转向角和横摆角速度;αf,peak、αr,peak分别表示前后轮胎的侧偏角峰值。

4 轮胎侧偏角控制器

轮胎侧偏角控制器应使轮胎侧偏角跟踪预定的参考值。该控制器由上层控制器和下层控制器两部分组成，上层控制器计算所需的横摆力矩以跟踪所需的轮胎侧偏角，而下层控制器计算从上层控制器生成的横摆力矩所需的制动输入。

在本文中，通过计算每个轮胎侧偏角的误差得到跟踪期望轮胎侧偏角的横摆力矩。上层控制器计算转向不足和过度转向两种工况下所需的横摆力矩。当首先预测转向不足时，跟踪所需的前轮侧偏角的横摆力矩计算如下：

(11)

其中:eαf表示期望前轮侧偏角与实际前轮侧偏角之间的误差;k1表示前轮侧偏角的误差增益，Mz,under表示转向不足情况下的直接横摆力矩输入。

当预测过度转向时，跟踪期望后轮侧偏角的横摆力矩计算如下：

(12)

其中:eαr是期望后轮侧偏角与实际后轮侧偏角之间的误差;k1表示后轮侧偏角的误差增益;Mz,under表示过度转向情况下的直接横摆力矩输入。

假设制动力矩与制动压力成正比，由此可计算出每个车轮的制动输入。下层控制器通过计算每个车轮的制动输入，从而产生所需的横摆力矩。

5 仿真结果

本文通过在Matlab中建立仿真模型来验证所提出算法的有效性。通过设定2种不同的仿真场景研究了该算法相对于非受控车辆的横向稳定效果：① 恒速开环正弦转向输入;② 零节气门低摩擦道路双车道变换。

为了评估运动预测的有效性，在非预测情况下，当其中一个车轮的轮胎侧偏角超过峰值时进行控制，并与运动预测的情况进行对比。

5.1 开环正弦转向输入

如图6所示，对恒速跟踪和开环双正弦转向输入进行仿真。图6(a)为每种情况下的车速，不进行控制的车辆速度急剧下降，因为车辆横向状态发散，没有运动预测的控制器使用严苛的制动方式，导致了速度的波动，而基于运动预测的控制器较早进行减速，使得速度的波动较小。

从图6(c)和(d)可以看出，基于运动预测条件下时，前后轮的侧偏角在很大程度上受到峰值限制，而非控车辆的侧偏角是发散的。

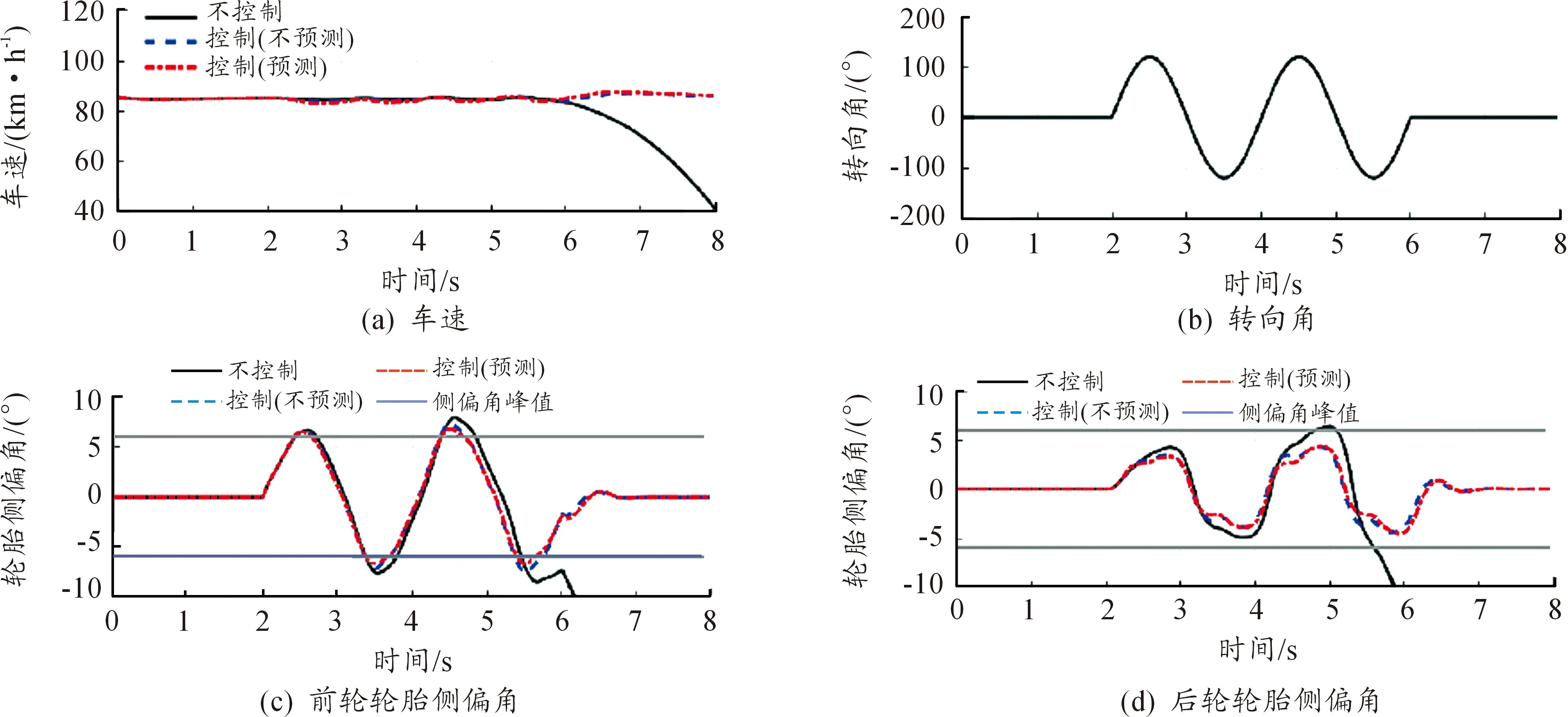
图6 开环正弦转向(车辆状态)

从图7可以看出，与不进行运动预测的控制器相比，采用运动预测的算法可以使制动力矩保持较小的水平。

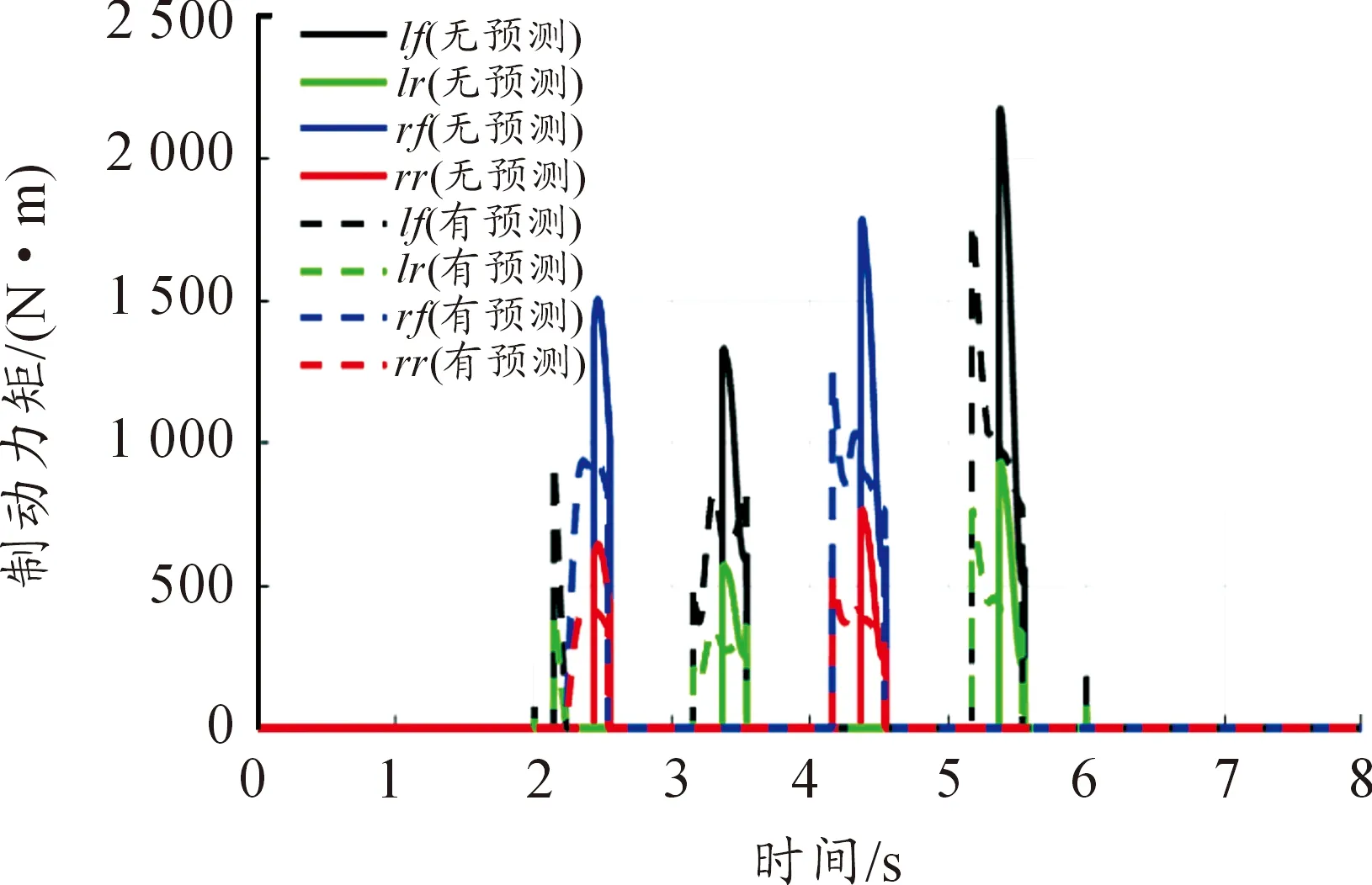
图7 开环正弦转向(控制输入)

5.2 低摩擦双变道

为了显示在闭环驾驶员模型情况下所提出的系统与传统的非预测系统之间的性能差距，建立了低摩擦道路(μ=0.6)的双车道变换情况的仿真场景。仿真结果如图8所示。图8(a)表示的是每种情况下的车速，由图可知，非控车辆由于横向不稳定使得车速显著下降，基于运动预测控制的车辆速度变化小，车辆状态明显更加稳定。图8(b)显示了3种情况下的转向角输入。图8(c)和(d)表明在运动预测的条件下，前后轮侧偏角受限在峰值之下。

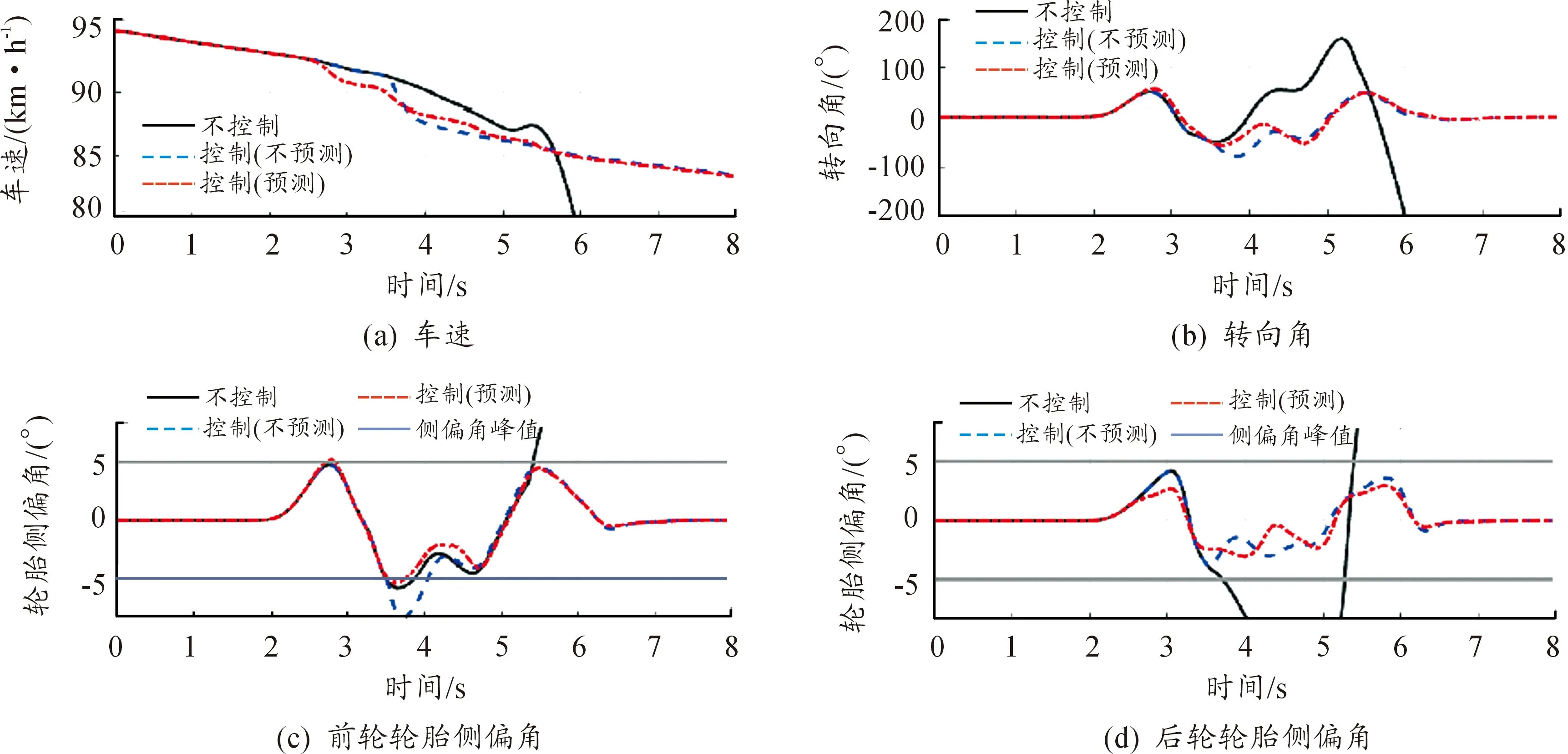
图8 双车道变换(车辆状态)

由图9可知，相比在发生不稳定之后接合的传统控制器，所提出的具有运动预测的算法采用的制动力矩更小。

图9 双车道变换(控制输入)

6 结束语

本文基于车辆横向动力学特性，采用运动预测和直接横摆力矩控制相结合的方式，设计了一种保证车辆横向稳定性的控制算法。为了验证控制系统的有效性，设计了不同工况的仿真试验。仿真结果表明，本文设计的横向稳定控制系统可以预先设定不稳定工况，从而进行离线求解，使得控制的实时性较高；在不同仿真工况下，该控制器能使车辆的轮胎侧偏角处于线性区，且与没有运动预测的控制器相比，控制执行所需的制动力较小，可以提高车辆的横向稳定性。