基于贝叶斯最大熵和辅助信息的土壤重金属含量空间预测
费徐峰,任周桥,楼昭涵,肖锐,吕晓男*
(1.浙江省农业科学院数字农业研究所,杭州 310021;2.农业农村部农产品信息溯源重点实验室,杭州 310021;3.浙江大学海洋学院,浙江 舟山 316021;4.武汉大学遥感与信息工程学院,武汉 430072)
土壤是人类生存和发展的物质基础,是粮食安全和人类健康的保证。近几十年来,随着快速的城市化和工业化进程,包括重金属在内的土壤污染物增加已成为社会发展和人类健康的重要障碍[1]。重金属通常具有持久的生物有效性并且在土壤中有较长的滞留时间,它不仅会积累在农业土壤中,导致土壤肥力降低、土壤生物学退化和作物生产力降低[2],而且也容易通过呼吸、皮肤接触或摄入等暴露途径进入动植物和人体内,并通过食物链进行生物放大,给食品安全和人类健康带来巨大风险[3]。
目前,对土壤重金属的研究主要关注其污染特征、空间分布和来源解析。其中重金属空间分布研究通过地统计方法来预测未采样位置的值。地统计学目前被广泛应用于土壤、环境和生态学的研究当中,它是识别重金属污染区域的有效、直观方法[4-5]。克里金(Kriging)法是目前地统计学中应用最广的方法之一,其原理是通过计算预测点与采样点的空间关联性,并使估计方差最小化来对预测位置进行无偏估计[1]。然而,大多数地统计方法(包括克里金法)并未完全考虑对空间预测很重要的先验信息,并且难以轻易处理能够提供辅助信息的大量相关知识(如同时处理数值变量和分类变量),因而限制了它们组合各种数据进行更准确的估计的能力[6]。
本文采用贝叶斯最大熵(Bayesian maximum entropy,BME)[7]将土壤母质类型作为辅助信息,来提高土壤重金属的空间预测精度。BME作为一种相对新颖的地统计学方法,能够有效地综合利用各种类型数据,从而提高预测的准确性。这些数据能以不同的形式表达,如区间、概率密度函数(probability density function,PDF)等[8]。不同于其他传统的统计方法,BME还具有以下优点:1)不需要数据满足基本的概率密度假设,即非高斯定律也可以应用于统计分析;2)可以处理空间和时间非平稳数据的预测,并可将物理规律和各种辅助信息(BME被称之为软数据)引入预测过程;3)能得到不同的分布图(如期望值、95%预测区间、残差等)[9-10]。本文在描述研究区土壤重金属基本污染特征的基础上,重点对比了BME与普通克里金(ordinary Kriging,OK)法对土壤重金属的预测精度,为综合利用辅助信息来提高土壤重金属预测精度提供新的研究思路。
1 材料与方法
1.1 研究区概况
本文选取浙江省杭州市为研究区。杭州位于中国东南沿海(29°11´~30°33´N,118°21´~120°30´E),是浙江省的省会城市,也是长三角城市群中的重要城市之一,面积约16 596 km2,总人口约919万。杭州属于亚热带季风气候区,夏季炎热潮湿,冬季寒冷干燥;年平均气温和相对湿度分别为17.8℃和70.3%,年均降水量和日照时数分别为1 454 mm和1 765 h。其东北部属浙江北部平原,海拔低平,土壤肥沃,河网密布,是杭嘉湖平原和萧绍平原的重要组成部分;西南部属浙西中低山丘陵,地形复杂。
1.2 数据来源
根据当地不同土壤母质的分布和面积情况,按面积等因素确定不同母质类型所需要的采样点数,同时结合第二次土壤普查的相关资料及实地调查,综合考虑海拔、地形地貌、土地利用类型及采样点的代表性和可操作性等因素,预布设500个采样点。在实地采样过程中,根据预设点周边环境进行适当调整,采用全球定位系统(global position system,GPS)记录采样点实际位置,形成采样点分布图(图1)。每个采样点的采样深度为0~20 cm,在附近10 m范围内采集5个子样本,充分混合,从而获得具有代表性的土壤样本。将土壤样品在室温下风干,研磨至过100目网筛,进行重金属元素全量化学分析。土壤中重金属含量采用标准方法测定,其中:铬(Cr)、铅(Pb)、镉(Cd)和砷(As)通过硝酸-高氯酸混合消解,采用电感耦合等离子体质谱(inductively coupled plasma mass spectrometry,ICP-MS)法测定[11];汞(Hg)通过硝酸-过氧化氢微波混合消解,采用原子荧光光谱法测定[12]。通过加入随机重复样品和标准样品对重金属含量测定过程进行质量控制[13],标准样品的回收率在90%~110%之间,重复样品的相对标准偏差在3%~8%之间。
杭州市土壤母质二级分类数据提取自浙江省土壤数据库[14],该数据库是以浙江省第二次土壤普查中编制的1∶5万比例尺土壤图件为基础,在搜集、整理数据资料的基础上,进行图形扫描、矢量化处理,按照统一的数据库建设标准而建成的具有正确拓扑关系的土壤数据库,其分布如图1所示。
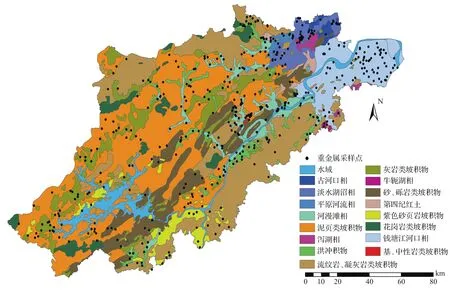
图1 杭州市土壤母质及重金属采样点分布图Fig.1 Distribution of soil parent materials and sampling points of heavy metals in Hangzhou City
1.3 空间预测方法
1.3.1 普通克里金插值法
作为一种传统的地统计预测技术,OK已成功应用于土壤科学,特别是对土壤重金属的空间预测中[1,11]。它是在有限的离散数据基础上实现对空间数据最优线性无偏估计的工具,是探索变量在空间上的分布结构和变异特性的有效研究方法[15]。它通过半方差函数来计算并模拟采样点的可变性,从而预测未知位置的值,并可通过多种模型(高斯、指数、球形等)进行拟合[16]。经验半方差函数计算公式如下:

1.3.2 贝叶斯最大熵法
BME在时空随机场的理论框架[17]下同时考虑多种数据的自相关和相互关系,支持多种数据表示方式(如区间、PDF等)来引入软数据(辅助信息),从而提高统计分析和预测制图的精度[7-9]。BME主要分为先验、后验和成图3个阶段。
1)先验阶段:基于现有的一般知识(如自然定律、数学期望、半方差等),通过最大熵原理最大化期望的信息数据。熵通常用于描述系统的不确定性,公式为:

式中:S(X)和S(p1,p2,…,pn)是熵的函数;pi是事件i发生的概率。当引入连续变量m(x)时,熵的函数可以变形为:
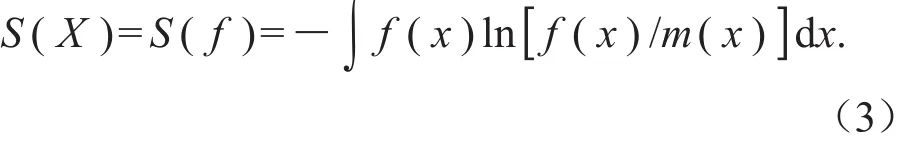
2)后验阶段:综合研究区的具体数据并基于贝叶斯条件概率原理,对第一步中的先验概率密度函数进行更新,以获得预测位置的后验概率密度函数。这一阶段应用的数据可以分为两大类:硬数据和软数据。本研究中的硬数据是指通过化学分析得到的土壤重金属含量,具有高置信度,软数据是指与土壤重金属含量有关的土壤母质类型信息[18-19]。后验概率密度函数计算公式如下:
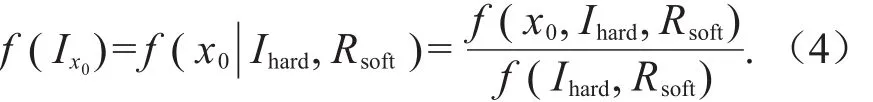
式中:f(Ix0)是预测位置x0处的概率密度函数;Ihard和Rsoft分别是预测点一定范围内的硬数据和软数据。在本研究中土壤母质类型以区间方式的软数据引入,所以后验概率密度函数可以转换为:
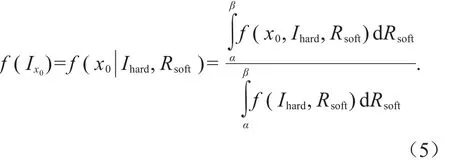
土壤母质类型具体的引入方式为:将采样点根据土壤重金属含量M等分为n组,将土壤母质根据不同的类型划分为不同的种类Z,记录预测点x0处对应的土壤母质所属的类型Zi,那么x0处根据土壤母质类型所计算的软数据概率为

式中:Rsoft是软数据的概率函数;Counti是属于土壤母质类型Zi的样点个数;Count(n)i是同时属于土壤母质类型Zi和重金属含量分组Mn的样点个数。
3)成图阶段:根据以上2步计算,由于得到的预测结果是概率密度函数,所以根据研究目的可以生成不同的空间分布图(如期望、众数、中位数、95%置信区间等)。
1.4 预测结果比较指标
通过十折交叉验证(将数据集等分成10份,轮流将其中9份作为训练集,1份作为验证集,10次试验结果的正确率的平均值作为对算法精度的估计)检验OK和BME插值方法对土壤重金属空间预测的精度。以平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)2个指标来进行比较,计算公式如下:

式中:n为样点的个数;yi和xi分别表示预测值和实际值。MAE和RMSE越小,表明该方法的预测精度越高。
2 结果与讨论
2.1 土壤重金属含量描述性特征统计
表1展示了土壤中重金属含量的基本统计特征及浙江省土壤环境背景值[20]和国家《土壤环境质量标准》(GB 15618—1995)的二级标准值。As、Cd、Cr、Hg和Pb的质量分数范围为2.63~43.20、0.05~1.41、10.32~104.00、0.03~0.50和16.90~62.60 mg/kg,其平均值分别为9.00、0.27、52.88、0.13和31.67 mg/kg,均低于二级土壤环境质量标准值,表明重金属不存在超标现象。但与浙江当地环境背景值相比,尽管Cr、Hg和Pb的平均含量低于相应的背景值,但是As和Cd的平均含量都高于背景值,分别是背景值的1.31倍和1.59倍,这可能是由于过去几十年的工农业生产活动和城市化进程所造成的污染积累[18,20]。各重金属的变异系数排序为Cd(80%)>As(69%)>Hg(61%)>Cr(38%)>Pb(28%),Cd、As和Hg较高的变异系数表明其在空间分布上存在很大的差异性,说明它们受到了人类活动的强烈干扰。此外,根据偏度和峰度值及Kolmogorov-Smirnov正态性检验(P<0.01),各重金属含量均呈非正态分布,所以在空间插值前对重金属含量进行了标准正态转换。

表1 杭州市土壤重金属含量描述性统计Table 1 Descriptive statistics of soil heavy metals in Hangzhou City
2.2 半方差模型比较
图2展示了用OK和BME法对不同重金属计算得到的经验半方差(圆圈)和拟合得到的理论半方差模型(线条)。对比OK和BME法的半方差模型发现:用2种计算方法得到的Cr的块金效应结果相同,均为0,表明Cr存在很强的空间关联性,随机误差较小,受人为因素干扰较小。其余4种重金属在加入土壤母质信息的BME模型中其块金效应均小于OK模型,表明BME模型对重金属的空间结构具有更强的解释能力。此外,从OK模型中可以看出,Cd、As、Hg和Pb的块金效应较大,表明这类重金属存在较大的随机误差,其来源受人为因素干扰较大。
2.3 预测结果对比
由OK和BME法产生的重金属预测残差分布如图3所示。总体上,BME对于重金属空间预测的精度高于OK,表现为在0值处有更高的频率分布和更窄的残差区间。这种结果也得到表2中交叉验证下的MAE和RMSE证实。相较于OK,BME对Cr、Pb、Cd、Hg和As预测的MAE分别降低了13.82%、15.55%、1.87%、8.25%和19.45%,同时,RMSE分别降低了14.34%、19.72%、6.22%、9.56%和39.42%。由以上对比可知,与OK方法比较,利用土壤母质类型作为辅助变量的BME方法能有效提高土壤重金属预测精度。

图2 克里金和贝叶斯最大熵半方差模型对比Fig.2 Semi-variance model comparison of Kriging and Bayesian maximum entropy methods

图3 贝叶斯最大熵(BME)和克里金(OK)法预测的残差分布对比图Fig.3 Predicted residual distribution comparison of Bayesian maximum entropy(BME)and Kriging(OK)methods

表2 土壤重金属BME和OK预测方法的计算精度对比Table 2 Comparison of estimation accuracy of Bayesian maximum entropy(BME)and Kriging(OK)methods
2.4 土壤重金属空间分布
用BME法预测产生的土壤重金属空间分布见图4。从中可知,Pb和Hg具有类似的空间分布模式:均在东北部的城市地区重金属含量较高。快速城市化和工业化过程中造成的污染排放及交通运输带来的污染物沉降可能是当地Pb和Hg含量较高的原因[21-23]。Cd和As也表现出相类似的空间分布规律:在西南部和中西部农村地区重金属含量较高。与化肥和农药密集使用密切相关的Cd,通常被视为农业活动的标志性元素[24],所以农村地区的农业活动可能是造成当地重金属含量升高的原因[12,25]。此外,不同于As,Cd在中东部还存在一块明显的高含量区域,这与当地矿业活动密切相关[26]。由前文的半方差模型可知,Cr具有极好的空间结构性,同时其变异系数也相对较低,说明Cr的来源更主要是由于自然作用,受人为因素干扰较少。
3 结论与展望
本研究以杭州市土壤重金属含量为研究对象,将OK和结合土壤母质信息的BME方法进行对比分析,比较其对重金属含量预测的准确性。由于BME法结合了土壤母质辅助信息,它能够更好地拟合重金属的空间变异规律,对重金属预测的精度高于OK,具有更优的MAE、RMSE值和残差频率分布。Pb和Hg在杭州东北部的城市地区具有较高的分布。快速城市化和工业化过程中造成的污染排放及交通运输带来的污染物沉降可能是其污染来源。Cd和As在西南部和中西部农村地区存在明显较高的分布,农业活动可能是其污染源。Cd在中东部还存在含量较高的区域,这与当地矿业活动密切相关。

图4 基于贝叶斯最大熵(BME)预测的杭州市土壤重金属空间分布图Fig.4 Spatial distribution of soil heavy metals based on Bayesian maximum entropy(BME)prediction in Hangzhou City
本研究仅采用了土壤母质作为辅助信息来提高预测精度。考虑到BME法的多源数据融合能力,在今后的研究中还可以将与土壤重金属密切相关的其他土壤属性信息(如有机质、pH等)、人为因素信息(工业、农业、交通等数据)作为辅助数据引入,进一步提高预测能力。同时,考虑到能够使用辅助数据的克里金方法(如回归克里金)对于土壤母质这类面状分类变量的引入存在一定的困难,本文只比较了BME与OK的差异,在后续引入数值变量的研究中可以进一步比较其他克里金方法和BME法对于辅助数据的利用效率。

