利用函数的性质判定方程解的存在
徐可
摘 要 教材从学生熟悉的二次函数入手,建立二次函数零点与相应二次方程根的联系,然后归纳出方程的根即为函数的零点的结论,接着又通过对函数零点左右两侧函数值符号的研究得出了方程根存在的充分不必要条件——即方程根存在定理,最后应用这个条件解决了简单的方程根存在的判定。通过本节课学生会对方程的解和解方程以及函数与方程的关系有个全新的认识。同时本节课在“二分法求方程的近似解”和“算法”中都有着重要的应用,是中学重要思想方法“函数与方程思想”的理论基础。
关键词 函数;方程;零点;存在
中图分类号: 文献标识码:A 文章编号:1002-7661(2019)15-0174-01
问题是数学的心脏,也是引发学生思考和探究的源动力。课堂中,有了问题,学生在好奇心驱使下才能真正激发思维,实现知识的逻辑结构向学生的认知结构转化。因此,在教学过程中,我们可依据教学目标将教学内容设计成一系列问题,将这些问题由浅入深、由易到难、合理设计、适时呈现,引导学生通过问题的思考和探究来实现教学目标。
一、内容及内容解析
本节课是北师大版必修一第四章函数与方程的第一节。
本节课的核心概念是函数的零点,重点是根的存在定理的探究与应用。
二、目标和目标的解析
确定本节课的目标是:(1)理解方程的根与函数零点之间的关系。(2)通过图形的直观理解并会应用方程解的存在的判断方法。(3)经历方程根的存在条件的探究过程。(4)会利用函数的单调性判断零点的个数及所在区间。
要实现让学生理解应用根的存在定理的教学目标。主要通过问题设置让学生参与定理推演落实的过程,让学生感受到函数的零点个数决定了方程的解的个数,而连续函数在闭区间端点的函数值的符号决定着函数零点的存在性。在此过程中需引导学生观察二重零点的情况,区分解的存在性与唯一性,关注连续函数的条件应用。
三、教学过程设计
问题一:引例1、判断下列方程(1)2x+3=0;(2)x2-x-6=0的根是否存在若存在求出方程的解。
【设计意图】从学生熟知的一元一次、二次方程的解法入手,学生易用构造法给出答案,这时可启发是否还有其它解法?引导学生从图形直观角度考虑问题。初步体会方程的解即是图像与X轴的交点。
引例2:求方程3x-x2=0的实数解。
【设计意图】引发学生的认知冲突,进而启发学生要研究困难的问题可以从特殊、简单的问题出发。
问题二:1、对引例1的再探究:
方程2x+3=0和方程x2-x-6=0的解从图像上看有什么特点?
【设计意图】通过函数与方程的联系及图象,进一步体会方程的根即是图像与X轴的交点,从而引入新概念——函数的零点。
思考1:为什么称为函数的零点?
思考2:函数的零点两侧函数值的符号有什么特点?
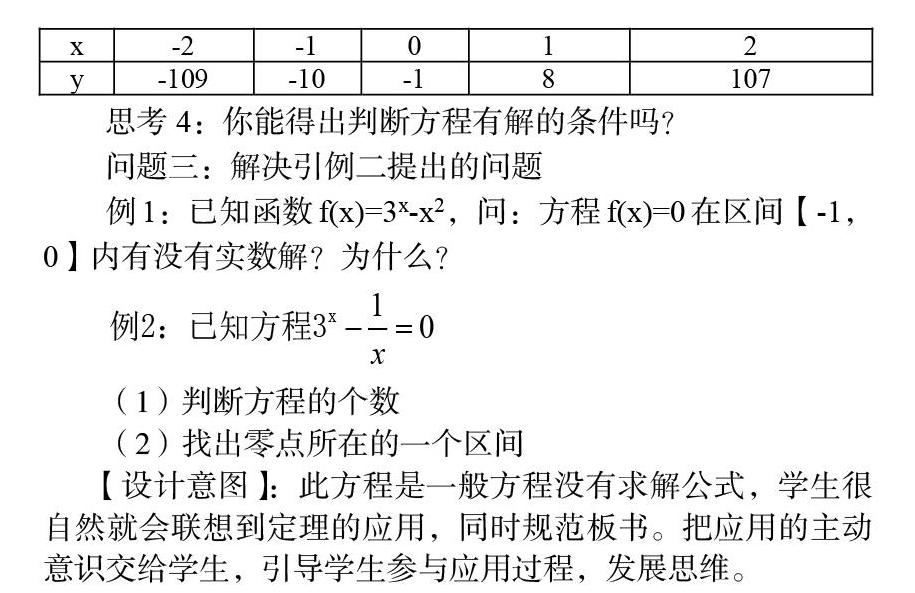
思考3:观察下表,分析函数在定义域内是否存在零点
x -2 -1 0 1 2
y -109 -10 -1 8 107
思考4:你能得出判断方程有解的条件吗?
问题三:解决引例二提出的问题
例1:已知函数f(x)=3x-x2,问:方程f(x)=0在区间【-1,0】内有没有实数解?为什么?
【设计意图】:此方程是一般方程没有求解公式,学生很自然就会联想到定理的应用,同时规范板书。把应用的主动意识交给学生,引导学生参与应用过程,发展思维。
四、小结
(一)零点的概念。
(二)方程在给定闭区间上是否有实解的判断方法:
1.确定函数的图象在给定区间【a,b】上是连续不断的。
2.计算f(a)f(b)的值并判断其符号。
3.若f(a)f(b)<0,则有实解。
4.有些問题除用上述方法外还需结合函数的图象来作出判断。
五、教学反思
(一)本节课借助一次函数,二次函数的图象与x轴是否有交点的情况与一元二次方程的根的关系出发,建立一元二次方程的根与相应的二次函数的零点的联系,然后将其推广到一般方程与相应的函数的情形,引入了函数零点的定义,体现了从具体到一般的思维过程。随后,利用函数图像和四个思考引导探索函数零点的存在,初步得到函数零点存在的判定方法,体现了数形结合的思想方法。
在教学过程中,虽然导课花费时间有点长,但是从学生对例题的反应能感受到,学生已掌握了通过函数性质判断方程根的存在性的方法。并体会到了根的存在性定理的生成过程,和定理中需注意的问题。
(二)改进措施:
在环节一:函数与方程的关系中可以台阶铺的再多一些,引出零点概念的过程中,学生配合不是很好,应快速调整,令y=0,则函数就变成了方程。给出函数零点的定义。
环节二:不用再分析引例中的函数图像特征,直接抛出3个思考问题,让学生自己去发现图像特征,这样可以节约导课时间。

