如何借助导数及其应用培养数学思维

隋玉霞

【摘要】导数的几何意义应用了曲线的切线思想，导数的代数意义应用了变化快慢的数学思想，将数学知识转化为学生的认知结构，进而培养学生的数学思维，就要设置一些问题情境，让学生通过观察与分析构建起自己的认知体系.

【关键词】导数;数学思维;数形结合

数学以最简约、最概括的方式反映着人类对事物数量关系及空间位置关系的认识，是科学真理的客观反映.通过数学教育，培养实事求是、言必有据的数学思维形式，为学生接受高等教育打下坚实的基础.导数是对函数性质的一个研究途径，也是高等数学中微积分的核心概念.通過导数的学习培养学生数学思维，首先要了解导数中蕴含的数学思想，然后再由教师设计教学模式进行有针对性的培养.

一、导数中的数学思想

教材当中设计了两条线索作为导数的起源，一个是自然界中广泛的变化现象;一个是变量变化速率的几何表示.这也说明，导数中蕴含着数形结合的思想、变化的思想.

二、如何通过教学设计培养学生的数学逻辑思维

（一）重视知识结构到认知结构的转化

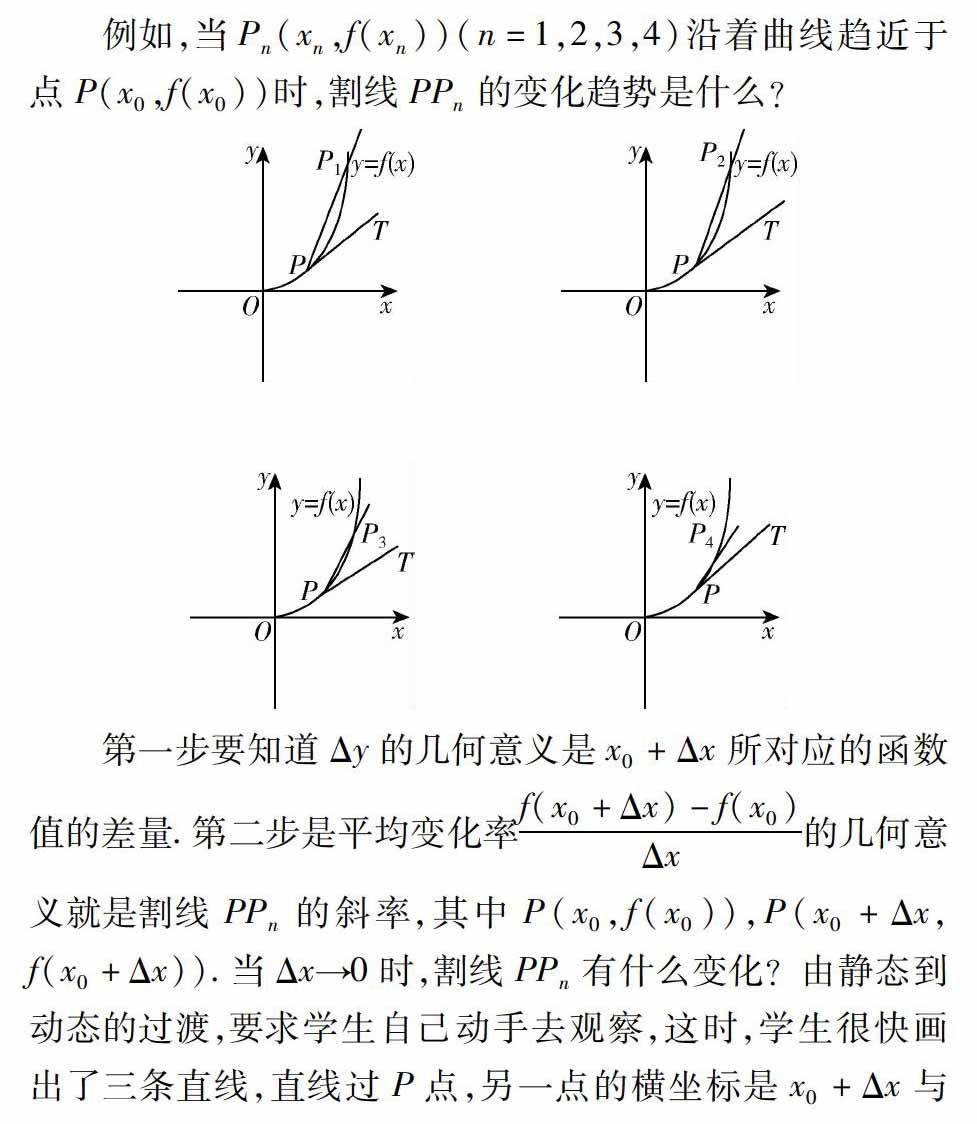
数学知识结构是由数学概念和命题构成的，要将这些新的知识结构转化为学生的认知结构，只有通过学生的动手观察、探索，将新的知识结构与旧的知识结构建立联系，例如，导数数形结合的切线表示法，以及导数的变化快慢的代数表示法，就是用旧知识解释新知识，从而转化学生的认知结构的.

（二）从数学史的角度把握知识的形成过程

从数学史的角度来看，导数的发现与伽利略有关系，当时伽利略发现了自由落体运动的规律，可以根据加速度与时间的关系求出落体的瞬时速度，当△t很小时这个比值接近于时刻t的瞬时速度，这就是导数的启蒙.

【参考文献】

[1]梁霜.数形结合的思想在导数问题中的应用[J].数学学习与研究：教研版，2018（16）：155.