高压下不同结构的Zr3N4的弹性性质的第一性原理计算

吉扬琪， 苑晓丽， 万 鹏

(河海大学理学院, 南京 211100)

1 引 言

超硬材料指的是一种硬度方面可以与金刚石相比拟的材料. 在现代社会中，超硬材料由于自身硬度等物理和化学性质的优越性，在很多工具制造方面具有先天的优势，所以它在材料业一直占据着一个不可替代的重要地位. 这导致超硬材料一直是一些重要的科研领域里的热门研究项目，受到大家的青睐[1-6]. 锆氮(Zr-N)化合物作为一种超硬材料，具有优异的化学性能. 比如在切削刀具的制造中，ZrN涂层刀具因其优秀的切削性能而被大家所研究[7]. 同时它还具有较高的超导临界温度，所以它成为了一种良好的超导体材料[8]. 基于ZrN的耐腐蚀性，很多人尝试将其作为各种材料的涂层起到抗腐蚀的作用[9, 10]. 可以说，锆氮(Zr-N)化合物的性质具有很高的科研价值，研究清楚它的特性，有助于我们更好地利用它，并充分发挥它的价值.

鉴于氮化锆在基础科学技术方面应用的重要性，近几年来对这类材料的结构和物理性质的研究也非常多. Saha等人基于密度泛函理论的第一性原理计算研究了ZrN的电子结构、振动光谱和热力学性质[11]. Qin-Xue Guo等人采用局域密度泛函的赝势法在高温高压的条件下研究了一种与Th3P4相同结构的氮化锆(Zr3N4)的合金结构和电子性质[12]. 成娟等人利用平面波赝势密度泛函理论方法研究了高压下c-Zr3N4的结构性质和弹性性质[13]. Wang A J等人采用有效应变应力法计算出了Zr3N4在一些特定方面的性质[14]. 还有不少其他的科研人员对锆氮化合物性质进行过一些很有价值的研究[15-18]. 当使用无机晶体结构数据库时，我们可以发现这些晶体具有许多不同的晶格参数和空间群. 我曾经对零压下不同结构的同种物质进行过一些研究. 但是迄今为止，这些不同结构的晶体的弹性性质和电子结构在高压下并没有被放在一起进行统一的研究与对比. 因此，本文继续之前的研究，将弥补这一不足，对Zr3N4的几种不同结构在高压下的结构与性质进行研究并且比较分析.

基于密度泛函理论(DFT)赝势法的第一原理计算由于其简便性与优越性迅速发展成为物理、力学和材料科学领域中材料建模仿真的“标准工具”[19-22]. 利用密度泛函理论(DFT)和广义梯度近似(GGA)可以计算晶体的各种性质. 本文采用赝势密度泛函理论(PDFT)、广义梯度近似(GGA)和准谐德拜模型，分别建立Zr3N4的不同结构模型. 通过仿真预测，对Zr3N4的弹性性质和电子性质进行研究，并对其变化规律进行分析和总结.

2 计算方法

本文利用美国Accelrys公司基于密度泛函理论(DFT)赝势法制作的Materials Studio软件中的castep软件包进行计算. 搭建模型与计算中所使用的原子是Zr(4s24p64d25s2)和N(2s22p3). 搭建好的不同结构的晶体模型如图1所示. 计算所采用的方法是Pur-Burk- ErnZHOHF(PBE)和广义梯度函数(GGA)相结合的形式，选取同样的计算精度进行迭代，从而达到几何优化的效果. 最后找出该物质稳定的几何结构. 本次实验总共选取了3种不同结构的Zr3N4[23]，经过计算，找到了合适的截断能与k点如表1所示. 最终得到了这几种结构零压状态下稳定的几何结构的晶格常数如表2所示.

表1 本次实验中所选取的不同结构的Zr3N4的截断能与k点

Table 1 Parameters of Zr3N4, the cutoff energy (eV) and K point we chossed.

CompdSpace groupa(Å)b(Å)c(Å)V(Å3)Cutoff energy(eV)K pointZr3N4I4-3D6.74——————306.1850015x15x15PNA219.72910.8183.281345.3248015x15x15PNAM9.78810.8543.3350.594906x17x5

表2 不同结构的Zr3N4在零压下稳定的晶格常数和部分实验值(tw=这次工作中的值，exp=实验值)

Table 2 Data calculated in this work, some experiments data and the results of others of Zr3N4under zero pressure.(tw=this work, exp=experiment)

CompdSpace groupa(Å)b(Å)c(Å)Zr3N4TWExpI4-3DPNA21PNAMI4-3D6.7839.8239.8146.740[12]10.84310.8403.2913.294

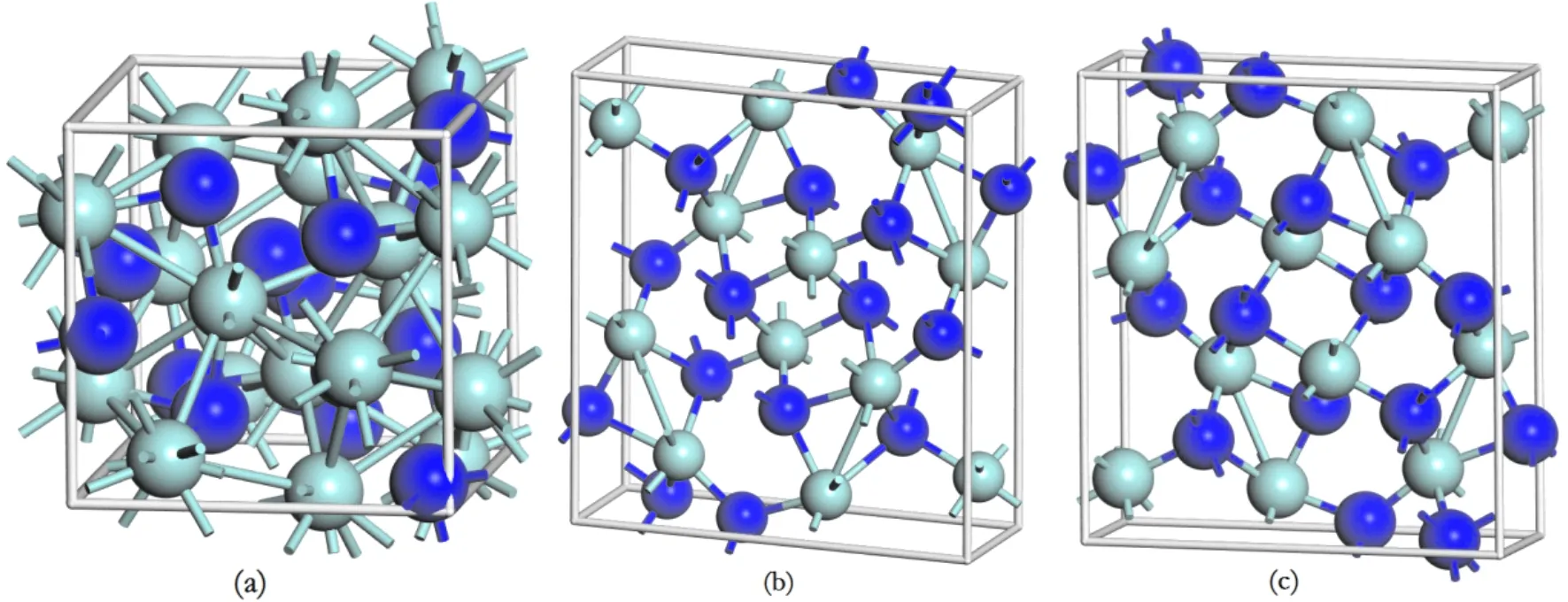
图 1 3种结构的Zr3N4晶体的结构图，(a)空间群为I4-3D的Zr3N4，(b)空间群为Pna21的Zr3N4，(c)空间群为Pnam的Zr3N4Fig.1 Primitive unit cells of 3 different Zr3N4, (a) Zr3N4 with space groups of I4-3D , (b) Zr3N4 with space groups of Pna21, (c) Zr3N4 with space groups of Pnam

3 结果与讨论

3.1 计算结果

固体的弹性常数在研究固体的物理性质方面有重要的意义，因为它与它们密切相关，比如弹性模量、理论硬度和德拜温度等[24-27]. 在得到这三种不同结构的Zr3N4的稳定的几何结构后，对这三种Zr3N4分别进行了加压，计算并记录其在不同压强下弹性模量Cij的数值. 这三种结构的Zr3N4属于2种不同的晶系，所拥有的独立的刚度矩阵元数目也各不相同. 空间群为I4-3D 的Zr3N4是立方晶系，只有3个独立的刚度矩阵元C11,C12和C44. 空间群为Pna21和Pnam的Zr3N4均属于正交晶系，它们有9个不同的刚度矩阵元，C11，C12，C13，C22，C23，C33，C44，C55，C66. 我们用B表示体弹性模量，G表示剪切模量. 在得到不同压强下的刚度矩阵元后，再通过计算公式，由Voigt近似和Reuss近似分别得到两种近似下的体弹性模量和剪切模量BV，BR与GV，GR. 计算公式如下[28, 29]：

对立方晶系：

(1)

(2)

(3)

其机械稳定性判据为：

C11>0,C44>0,C11>|C12|,(C11+2C12)>0

对于正交晶系：

(4)

(5)

BR=Δ[C11(C22+C33-2C23)+C22(C33-2C13)-2C33C12+C12(2C23-C12)+C13(2C12-C13)+C23(2C13-C23)]-1

(6)

(7)

Δ=C13(C12C23-C13C22)+C23(C12C13-C23C11)+C33(C11C22-C122)

(8)

其机械稳定性判据为：

C11>0,C22>0,C33>0,C44>0,C55>0,C66>0

C11+C22+C33+2(C12+C13+C23)>0.

C11+C22-2C12>0,C11+C33-2C13>0

C22+C33-2C23>0

在使用Voigt近似和Reuss近似计算弹性模量时，这两个值分别代表体积模量B(或者剪切模量G)理论计算的最大值和最小值，广泛采用的理论近似是Voigt-Reuss-Hill近似. 即取Voigt近似和Reuss近似的算术平均值，便达到与实际值较为吻合. 于是把由(1)-(8)式所得的BV，BR和GV，GR通过(9)-(10)式计算得不同结构的不同压强下的体弹性模量和剪切模量B与G.

(9)

(10)

接下来就可以根据式11和12求出杨氏模量(E)和泊松比ν

(11)

(12)

同时，在得只一个物质的体积弹性模量B和剪切模量G时，根据Pugh判据[30]，当它们间的比值(B/G)小于1.75时，材料呈现出脆性，当比值大于等于1.75时，材料呈现延展性. 于是计算出各个材料的B/G.

所有的实验结果数据均列于表3-6中，并且绘制了相关数据的变化曲线,如图2-3.

3.2 弹性性质讨论

首先这三种结构的Zr3N4在0-80 GPa的压强下都是保持力学稳定的. 从图2中可以看出，这三种不同结构的Zr3N4的弹性常数Cij均随着压强的增大而增大. 对于空间群为I4-3D的Zr3N4来说，C11受压强的影响产生的增量是明显大于C12和C44的. 这表明这种结构的Zr3N4在各个方向的可压缩性是各向异性的. 同理对于空间群为Pna21和Pnam的Zr3N4，它们之间的Cij数值相差不大，且他们的C22和C33都是受压力影响最大的两个分量. 可以说也是各向异性的. 这种差别的根源来源于各物质的不同方向的化合键的强度有差别，这几个方向的键强要强于另外的方向的键强，且数值越大则抵抗应变的能力也越大，所以它们这几个方向有较强的抗应变能力.

表3 空间群为I4-3D的Zr3N4在压强为0-80 GPa时的Cij值.

Table 3Cijof Zr3N4with space group I4-3D under the pressure from 0 to 80 GPa.

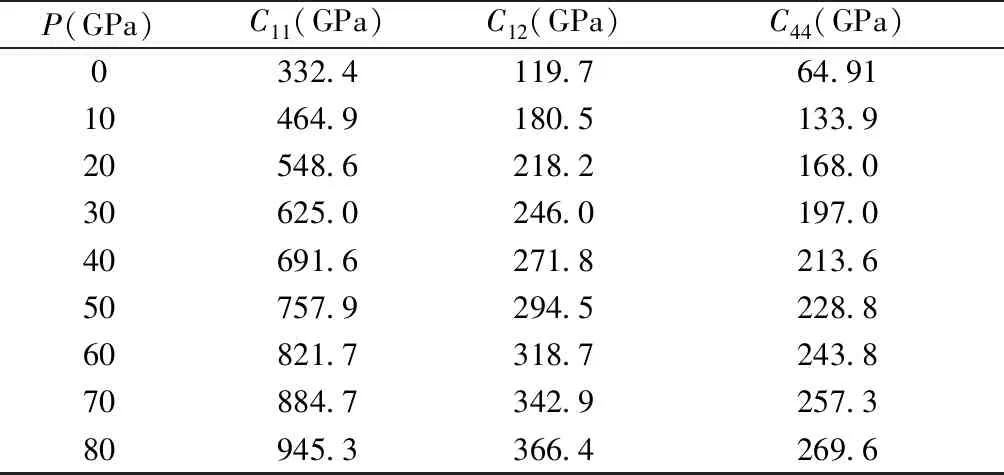
P(GPa)C11(GPa)C12(GPa)C44(GPa)0332.4119.764.9110464.9180.5133.920548.6218.2168.030625.0246.0197.040691.6271.8213.650757.9294.5228.860821.7318.7243.870884.7342.9257.380945.3366.4269.6

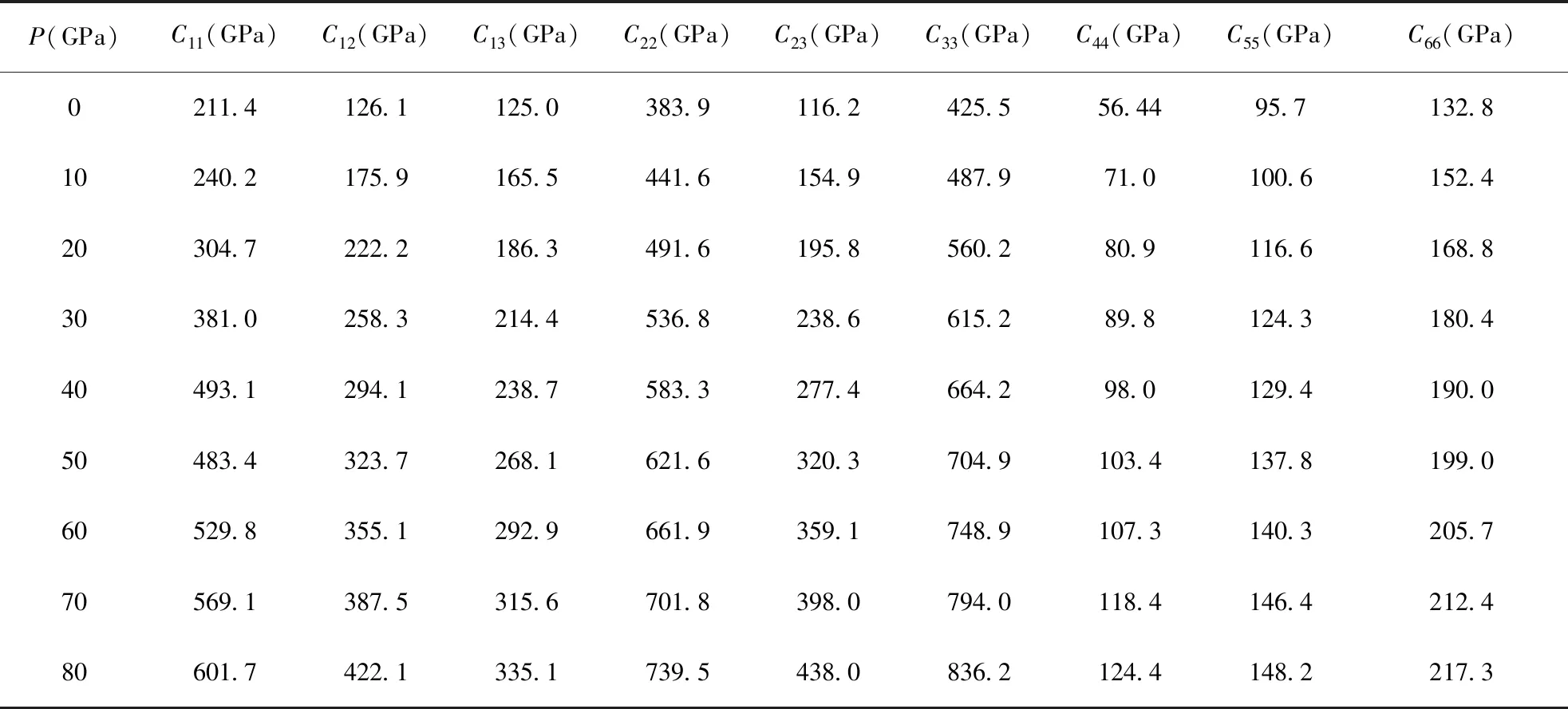
表4 空间群为Pna21的Zr3N4在压强为0-80 GPa时的Cij值.

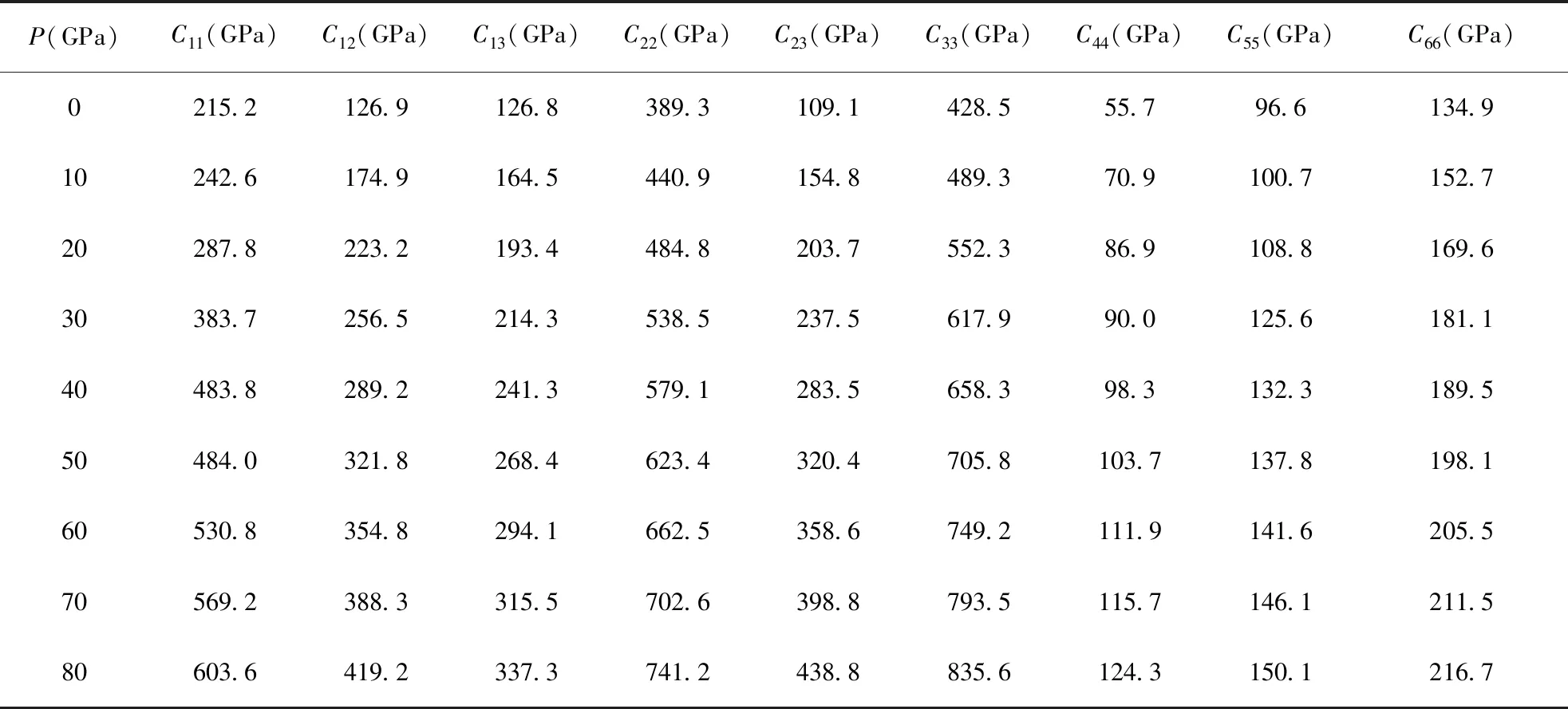
表5 空间群为Pnam的Zr3N4在压强为0-80 GPa时的Cij值.

表6 3不同结构的Zr3N4在压强为为0-80 GPa时的体弹模量B，剪切模量G，杨氏模量E，泊松比，B/G.

Table 6 Bulk modulus, shear modulus, Young’s modulus, Possion’s ratio andB/Gof Zr3N4under the pressure from 0 to 80 GPa.

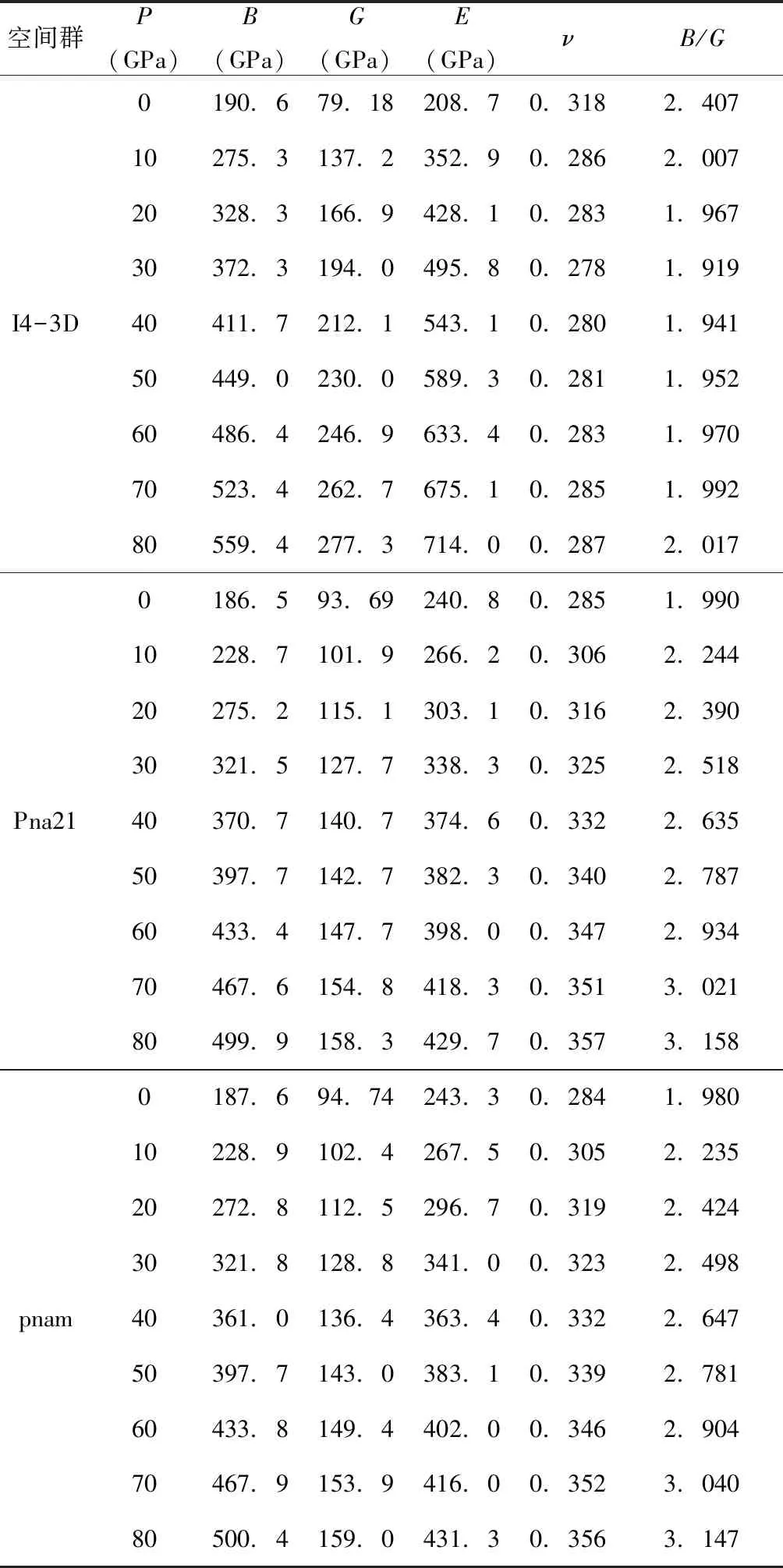
空间群P(GPa)B(GPa)G(GPa)E(GPa)νB/GI4-3D0190.679.18208.70.3182.40710275.3137.2352.90.2862.00720328.3166.9428.10.2831.96730372.3194.0495.80.2781.91940411.7212.1543.10.2801.94150449.0230.0589.30.2811.95260486.4246.9633.40.2831.97070523.4262.7675.10.2851.99280559.4277.3714.00.2872.017Pna210186.593.69240.80.2851.99010228.7101.9266.20.3062.24420275.2115.1303.10.3162.39030321.5127.7338.30.3252.51840370.7140.7374.60.3322.63550397.7142.7382.30.3402.78760433.4147.7398.00.3472.93470467.6154.8418.30.3513.02180499.9158.3429.70.3573.158pnam0187.694.74243.30.2841.98010228.9102.4267.50.3052.23520272.8112.5296.70.3192.42430321.8128.8341.00.3232.49840361.0136.4363.40.3322.64750397.7143.0383.10.3392.78160433.8149.4402.00.3462.90470467.9153.9416.00.3523.04080500.4159.0431.30.3563.147

从图3可以看出，不同结构的Zr3N4对应的体弹模量，剪切模量和杨氏模量都是随着压强的增大而增大的. 这代表它们都是力学稳定的. 体弹性模量代表了抵抗体积压缩的能力，体弹模量最大的结构时空间群为I4-3D的Zr3N4,证明了其抵抗体积压缩的能力强于另外两种结构. 空间群为pna21和pnam的Zr3N4的体弹模量在数值上较为接近，但是空间群为pnam的Zr3N4在大多数压强下都略高于pna21一点，表明这两种结构的Zr3N4抵抗体积压缩的能力相近，但是空间群为Pnam的Zr3N4稍好一点. 剪切模量(G)是一种用来表征材料抵抗变形能力的参量，杨氏模量则是反应材料刚度也就是抵抗线性压缩的能力的一个指标. 显然，在抵抗变形和线性压缩这一块依旧是空间群为I4-3D的Zr3N4拥有最强的能力. 而空间群为pna21和pnam的Zr3N4的剪切模量和杨氏模量在数值上均比较接近，但是空间群为pnam的Zr3N4在大多数压强下都略高于pna21一点，表明这两种结构的Zr3N4抵抗变形和线性压缩的能力相近，但是空间群为Pnam的Zr3N4更为优秀一点. 泊松比是一个反应材料横向变形情况的弹性常数，在0压时，空间群为I4-3D的Zr3N4的泊松比是大于空间群为pna21和pnam的Zr3N4，证明在0压条件下，主方向变形一定时，空间群为I4-3D的Zr3N4次方向的变形量大于另外两种结构的Zr3N4. 但是当压强增大时，空间群为I4-3D的Zr3N4的泊松比呈现出一个快速下降再缓慢上升的过程，而另外两种结构的Zr3N4的泊松比则随着压强的增大上升. 在压强大于10 GPa的时候，空间群为I4-3D的Zr3N4的泊松比低于另外两种结构. 泊松比的数值满足ν<0.26时，材料呈现脆，ν>0.26时，材料呈现延展性.B/G也是表征材料脆性的物理量. 对于B/G，当B/G小于1.75时，材料呈现出脆性，当比值大于等于1.75时，材料呈现延展性. 对比B/G的数值曲线，与泊松比的结论相同. 故不管压强为多少，这3种结构的Zr3N4均是延展性材料. 在0压下，空间群为I4-3D的Zr3N4延展性高于另外两种结构的Zr3N4. 在压强大于10 GPa的情况下，空间群为Pna21和Pnam的Zr3N4的延展性比空间群为I4-3D的Zr3N4的好，且这两种空间群的延展性相近.

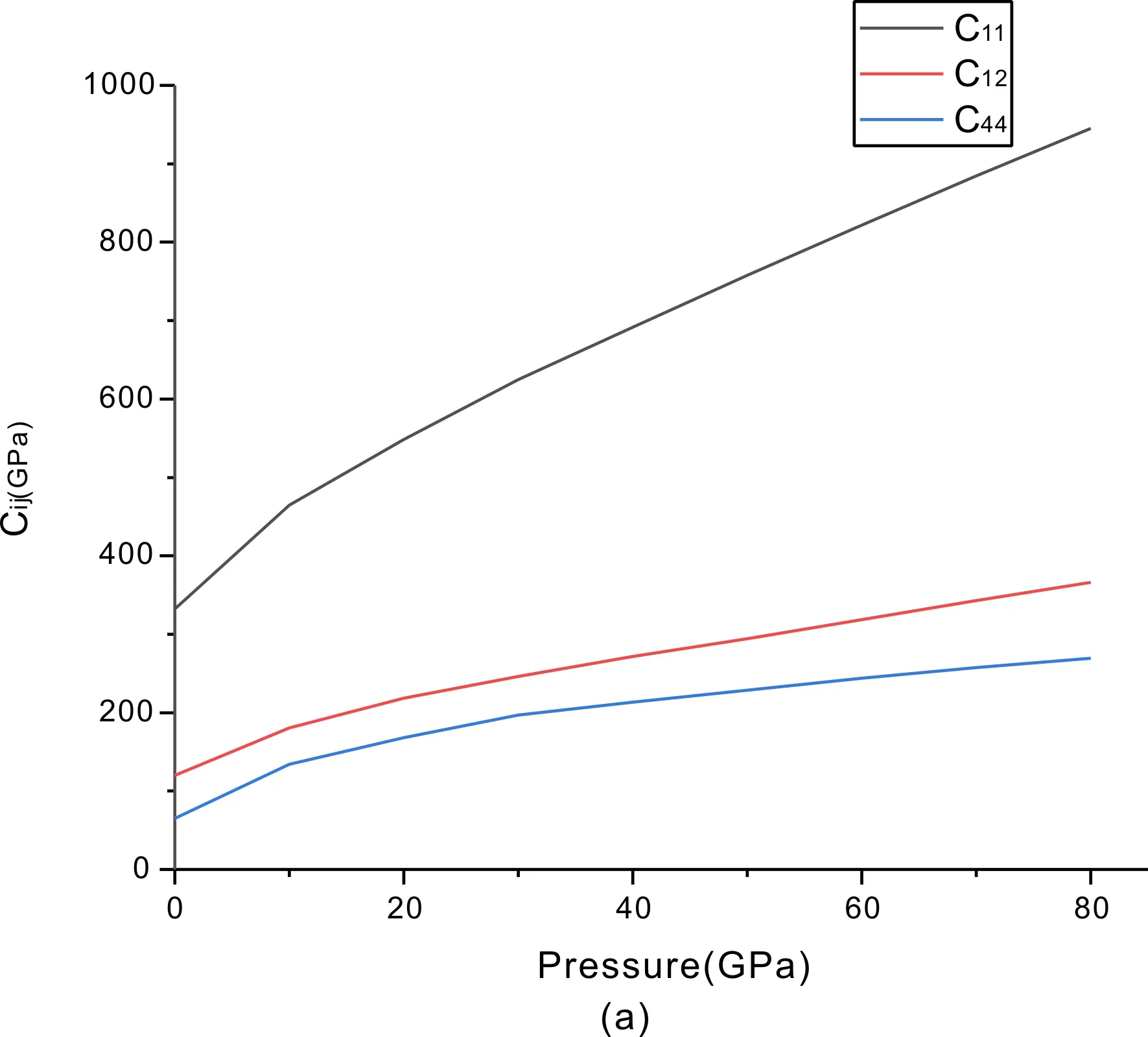
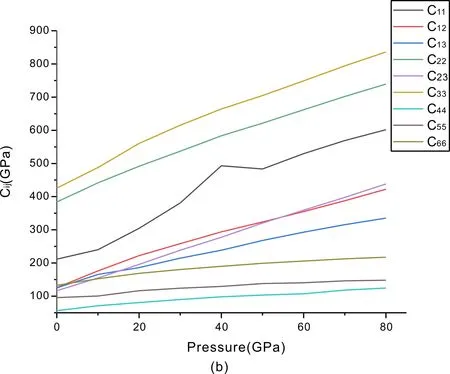
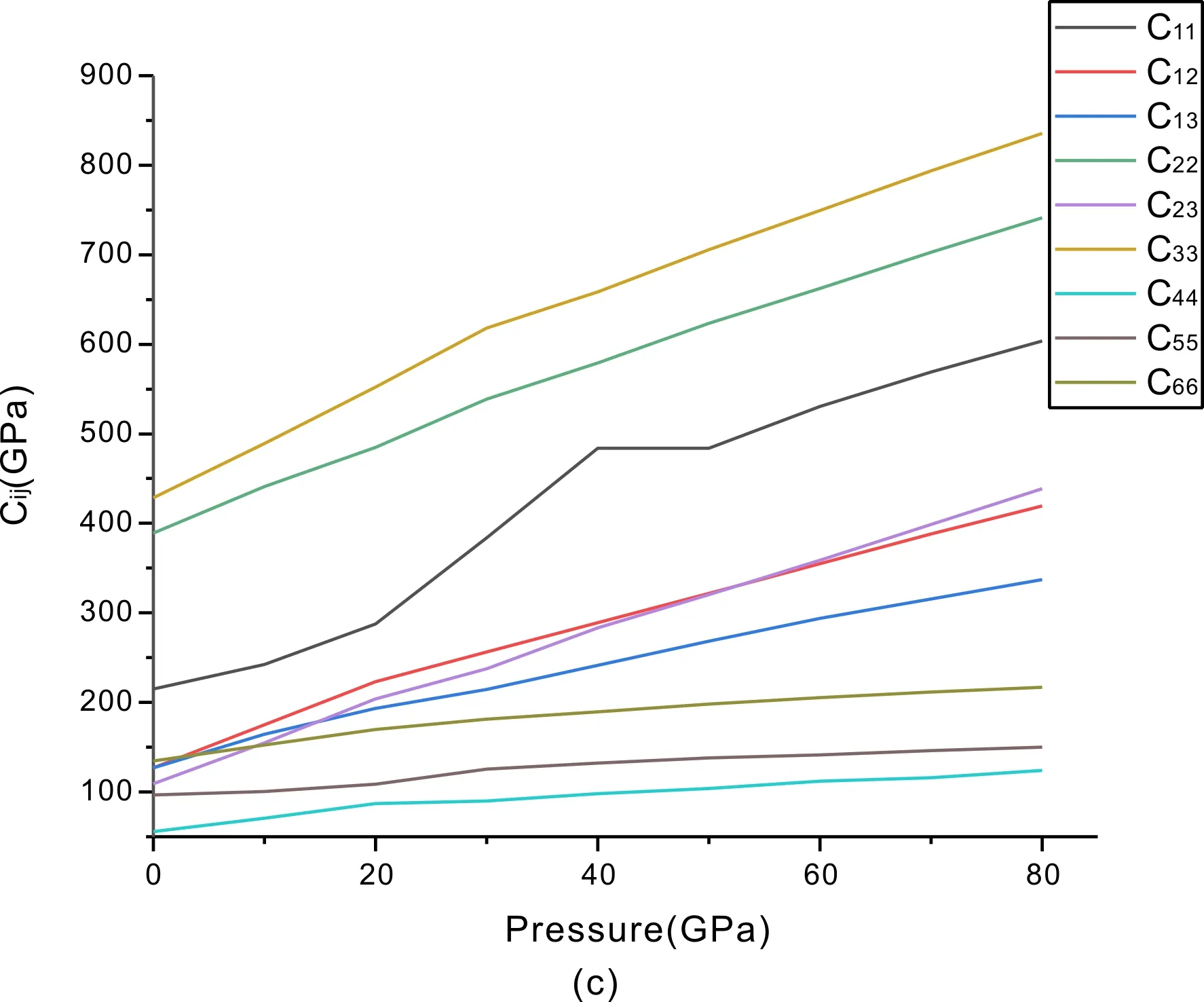
图 2 不同结构的Zr3N4的Cij在0-80 GPa压强下变化图：(a)空间群为I4-3D的Zr3N4，(b)空间群为Pna21的Zr3N4，(c)空间群为Pnam的Zr3N4

Fig.2 Cijof Zr3N4with different structures under the pressure from 0 to 80 GPa (a) Zr3N4with space groups of I4-3D, (b) Zr3N4with space groups of Pna21, (c) Zr3N4with space groups of Pnam

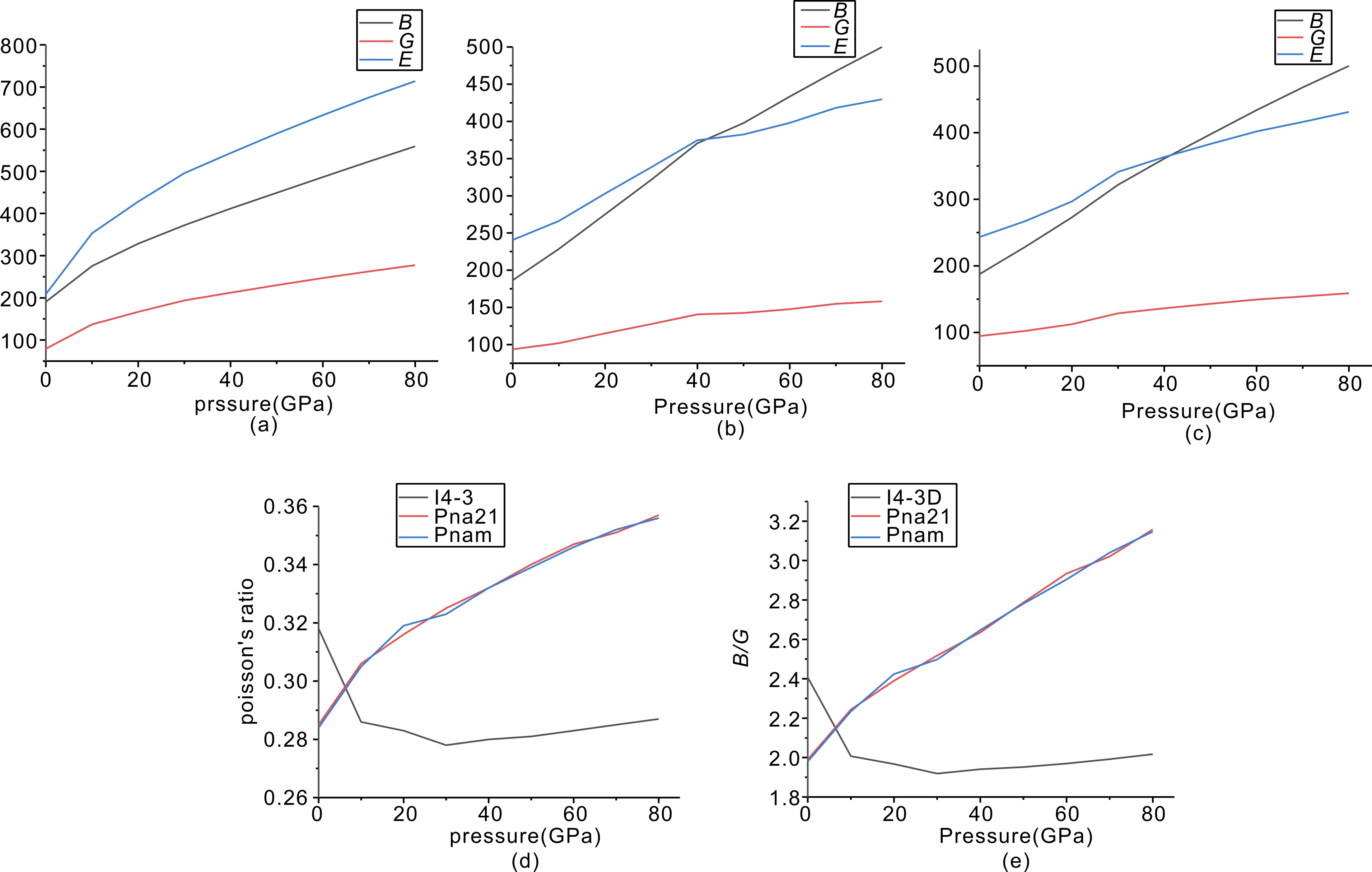
图 3 不同结构的Zr3N4的弹性模量(B)、剪切模量(G)、杨氏模量(E)、泊松比和B/G在0-80 GPa压强下变化图：(a)空间群为I4-3D的Zr3N4的B、G和E随压强的变化图，(b)空间群为Pna21的Zr3N4的B、G和E随压强的变化，(c)空间群为pnam的Zr3N4的B、G和E随压强的变化图，(d)三种不同结构的Zr3N4泊松比随压强的变化图，(e)三种不同结构的Zr3N4的B/G随压强的变化图

Fig.3 Bulk modulus, shear modulus, Young’s modulus, Possion’s ratio andB/Gof Zr3N4under the pressure from 0 to 80 GPa.(a)B,GandEof Zr3N4with space groups of I4-3D, (b)B,GandEof Zr3N4with space groups of Pna21, (c)B,GandEof Zr3N4with space groups of Pnam, (d) Possion’s ratio of Zr3N4, (e)B/Gof Zr3N4

4 结 论

本文采用了第一性原理的方法计算了0-80 GPa压强下3种不同空间群I4-3D，Pna21，Pnam的Zr3N4的弹性性质，包括体弹模量B、剪切模量G、杨氏模量E、泊松比和B/G. 结果表明，三种结构的Zr3N4在高压下都是保持力学稳定的，它们的弹性常数Cij均随着压强的增大而增大. 同时由于不同分量变化程度不同，表面它们的弹性变化存在各向异性. 空间群为Pna21和Pnam的Zr3N4各项数据比较相近，表明它们在高压下的弹性性质相近. 三种结构的Zr3N4对应的体弹模量，剪切模量和杨氏模量都是随着压强的增大而增大. 其中空间群为I4-3D的Zr3N4有最好的抵抗体积压缩，变形和线性压缩的能力. 泊松比和B/G比值的结果表明，三种材料均在各个压强下有较好的延展性. 其中零压下，空间群为I4-3D的Zr3N4有最好的延展性. 但是高压下，其延展性先下降再上升，在压强大于10 GPa时，其延展性不如空间群为Pna21和Pnam的Zr3N4好.