线型离子阱中空间电荷效应的理论分析

邵辉丽, 潘志兵 , 王顺治 , 任 莉

(1.上海工程技术大学数理与统计学院, 上海201620； 2.中国科学院上海天文台时间频率研究室, 上海 200030)

1 线型离子阱囚禁原理

线型离子阱由均匀分布于同一圆周上的四根电极和两个端帽电极组成. 四根电极杆上加射频交流电压V=V0cosΩt, 相对的两根施加的电压完全一样, 而相邻的两根电压幅值相同, 位相相反, 该射频电场实现离子在径向(x-y)平面内的囚禁. 安置在两端的帽极位置正对阱体中心轴, 此电极上施加极性和囚禁离子电荷相同的静电场, 利用静电排斥限制离子在轴向z方向的运动, 最终离子被囚禁于中心轴线附近[1]. 图1是线型离子阱结构示意图, 四根电极上加的射频交流电场如图2所示.

图1 线型离子阱结构图Fig. 1 The setup of linear ion trap

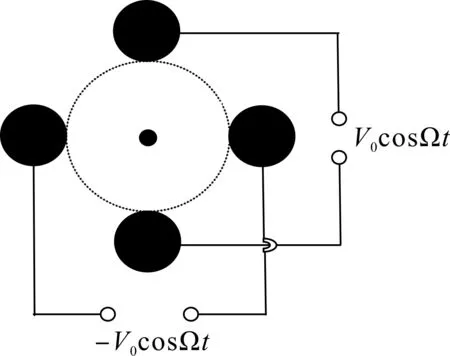
图2 电极连接示意图Fig. 2 The Schematic representation of electrodes connecting of linear ion trap

2 空间电荷效应的理论分析

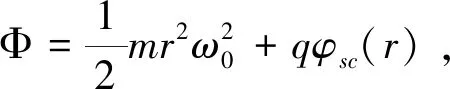
(1)

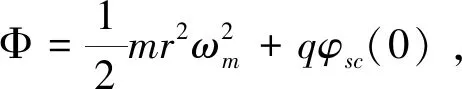
(2)

假设ωm(r)空间上变化不剧烈, 考虑用所有离子的运动频率的平均值〈ωm〉代替, 对方程(2)积分可得

(3)

(4)

对方程(4)微分后可得空间电荷产生的电场

(5)

在x-y平面上做久期运动的离子, 当它受到该电场库仑力作用时, 其运动方程为

(6)

在r=0附近做泰勒展开, 得到小振动近似[5]. 对展开结果取前三项, 得到以下的非线性振动方程：

(7)

修正后的运动频率

(8)

从(8)式可以看出, 考虑空间电荷效应后, 离子久期运动频率ωm与理论计算结果ω0之间有漂移, 漂移直接依赖于离子云的中心密度, 离子在阱内的运动频率降低, 如图3曲线所示. 单位体积内有大量离子存在时, 库仑排斥力使得离子在阱中难以稳定存在, 从而使阱内可以稳定囚禁的离子数有上限, 阱内可以稳定囚禁的离子总数：

(9)

(10)

实验条件：囚禁离子为199Hg+, 质量m=3.329×10-25kg, 电荷q=1.6×10-19C, 囚禁离子数目N=2×106,ω0/2π=50 kHz. 根据(10)式从而可以确定离子的温度, 离子云温度越低, 离子云半径越小, 电荷均匀分布在阱中心附近, 空间电荷效应明显, 久期频率漂移越大；温度越高, 离子之间的库仑相互作用减弱, 频率漂移越小, 与文献[6]中的结果保持一致.

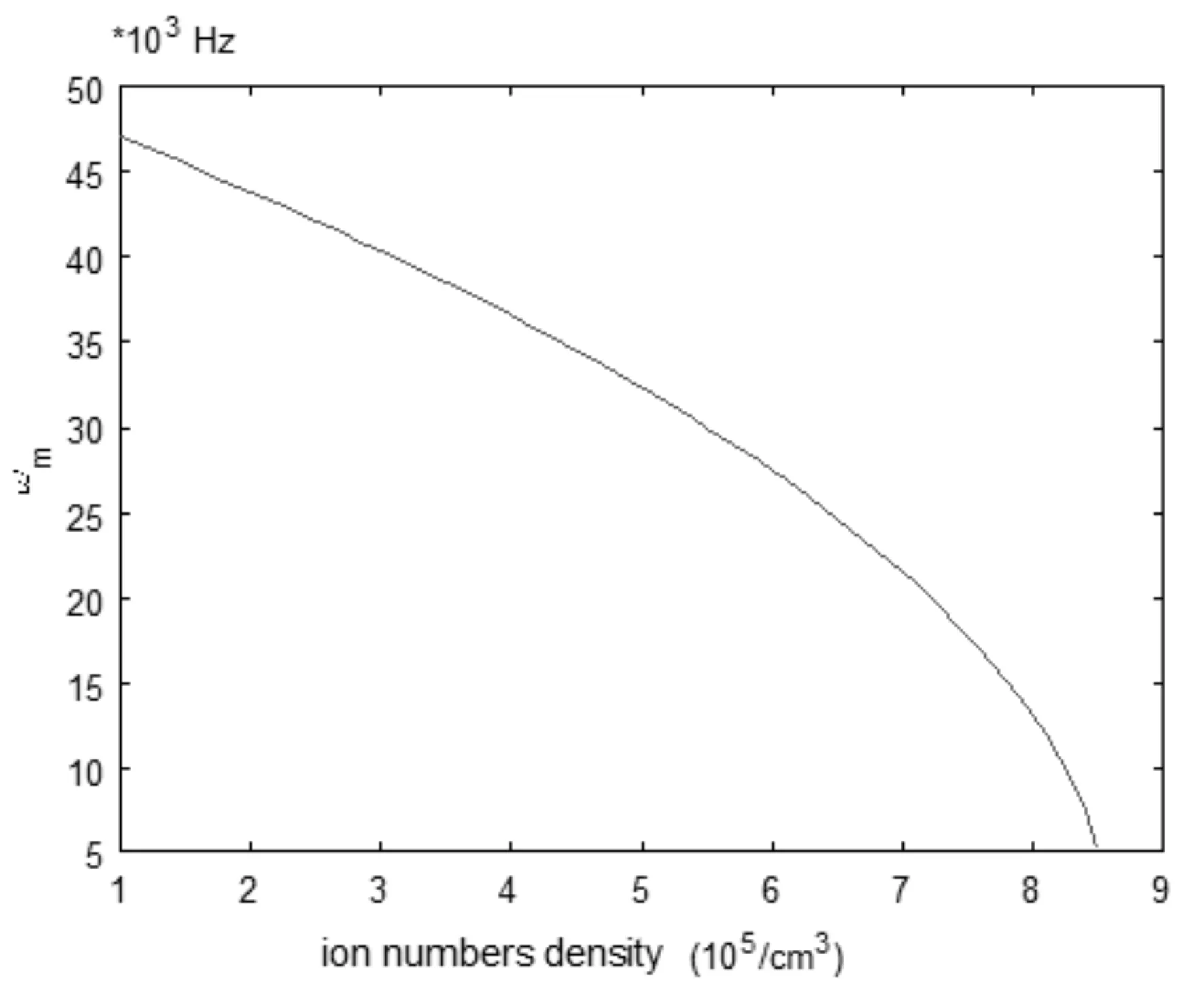
图3 离子久期运动频率和离子云中心密度的关系Fig. 3 The dependence of frequency shift on the central ion clouds density

图4 总电势随离子总数变化曲线Fig. 4 The total potential as a function of the number of ions

图4表明离子阱中总电势的变化依赖于离子到阱中心的距离, 不考虑空间电荷效应时, 电势与离子到阱中心的距离的平方正比, 考虑空间电荷效应后, 空间电荷产生的电势会削弱射频场电势产生的电场力对离子的束缚作用, 离子运动的久期频率不再是一个常数.

3 结 论

本文研究了离子阱中空间电荷效应对离子宏观运动久期频率的影响, 离子云中心密度越大, 离子间的库仑排斥越强烈, 离子运动的久期频率漂移大, 运动频率变小, 改变了离子的运动轨迹. 另外讨论了离子云的数目, 温度与实验参数之间的关系. 计算过程中采用了近似处理和离子云高斯分布假设, 近似结果与实际情况会存在偏差, 但对理解空间电荷效应对离子运动的影响以及后期用共振吸收方法检测离子时有重要的参考价值, 对用离子阱进行的频标实验、碰撞实验和其他方面的研究都很重要.