Cornish-Fisher展开在VaR中的应用

魏正元，李素平，李 乔，余愈灿

(重庆理工大学 理学院, 重庆 400054)

随着经济全球化的不断深刻演变，金融风险已不再是某个单一市场所面临的问题；因此，风险管理已经成为社会经济活动中必不可少的议题之一。随着金融市场的发展，G30集团在研究衍生品种的基础上，于1993年提出了度量市场风险的风险价值(value at risk，VaR)方法，该方法已成为目前金融界测量市场风险的主流方法。随后由J.P.Morgan[1]在1994年推出的用于计算 VaR的Risk Metrics风险控制模型更是被众多金融机构广泛采用。此后，学者们对VaR进行了大量的研究，并取得了丰富的成果。

目前对于VaR的计算主要有3种方法：历史模拟法，方差-协方差法， 蒙特卡洛法。根据历史数据估算VaR的方法主要有两种：第1种方法是选择一个最优的参数分布拟合数据，然后将VaR作为该分布的分位数即可得到，例如Sun和Hong[2]采用重要抽样的方法估计VaR；第2种方法是基于历史数据的经验分布或者核函数，运用非参数密度估计方法来拟合一个非参数的分布，然后从非参数的密度函数来估计VaR，例如Chang等[3]和Jeong等[4]运用非参数的方法估计了VaR。Abbasi等[5]运用蒙特卡洛法模拟Weibull、Burr XII、Birnbaum-Saunders和Pareto分布，计算了某保险公司数据的VaR并运用bootstrap方法构建了一个VaR控制图方案。Lien等[6]将分布的前4阶矩引入VaR的近似计算方法中，模拟比较了Cornish-Fisher、Edgeworth、Gram-Charlier和Johnson分布等4种方法下的VaR的近似效果。黄金波等[7]运用非参数核估计方法对资产组合的VaR进行了估计，并在大样本下，与Cornish-Fisher展开法进行了比较。本文将基于有偏分布拟合、Cornish-Fisher展开和Bootstrap来计算小样本情况下苹果公司收益率数据的VaR。

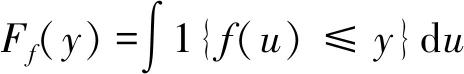
被称为函数f(x)的递增重排。重排过程将函数f(x)变换成其分位数函数f*(x)。递增重排的具体步骤为：将目标区间[a,b]进行充分小的等间距的划分，计算f(x)在每个间隔点的值，最后将所有值按从小到大的顺序排列。根据此方法来计算Cornish-Fisher展开的值。

1 VaR的计算

1.1 VaR的定义

VaR方法因其测量风险的定量性、综合性、简便性等优点，故而被诸多金融机构和监管机构广泛使用，目前已成为金融界测量市场风险的主流方法。若用随机变量L表示一个金融头寸在某持有期l内的损失(空头的损失为资产收益率，多头的损失为资产收益率的相反数)，FL(x)为L的累积分布函数，p表示概率水平((p∈(0,1)),常取值为95%或99.9%)，定义持有期l内概率为p的某金融头寸的VaR为

VaRp(L)=inf{x|FL(x)≥p}

在统计视角下，VaRp(L)即是损失随机变量L的上侧1-p分位数(或下侧p分位数)。对于标准化损失随机变量，若给定其分布函数为F(·)、概率水平p以及持有期l，那么根据随机变量的位移尺度变换，有

VaRp=μl+σlF-1(p)

这里：μl和σl分别表示损失随机变量在l期内的期望和标准差；F-1(p)为标准化损失随机变量的分位数函数。

1.2 基于有偏分布分位数的VaR计算

金融资产收益率在呈现出尖峰厚尾特征的同时，又存在一定的偏态[9]，此时，t分布、广义误差分布等对称分布将不能充分表现出数据的特征。Fernández等[10]定义了一种由对称分布导出有偏分布的方法(F-S有偏)：由单变量、对称的概率密度函数f(x)生成参数为ξ的有偏分布密度函数为：

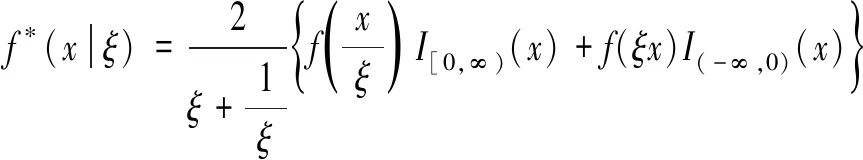
分布函数为

这里ξ∈(0,∞)。当ξ>1时，f*(x|ξ)为右偏分布；当ξ<1时，f*(x|ξ)为左偏分布；ξ=1时，f*(x|ξ)退化为对称分布(图1)。因此，损失随机变量基于分布分位数的VaR可表示为

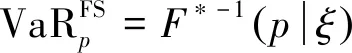
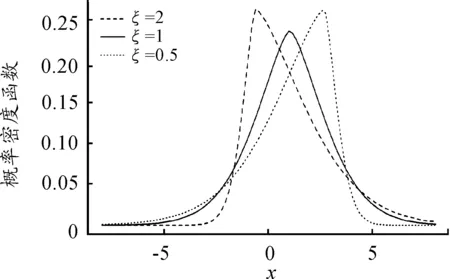
图1 对称的广义误差分布(ξ=1)和有偏广义误差分布(ξ=2和ξ=0.5)

1.3 基于Cornish-Fisher 展开的VaR计算

Dasgupta[11]在其著作中给出了一种连续的标准化随机变量分位数的渐近展开方法，即Cornish-Fisher展开。它是将一个真实分布的分位数函数展开为关于标准正态分布分位数函数的多项式函数，其前4阶展开式如下：

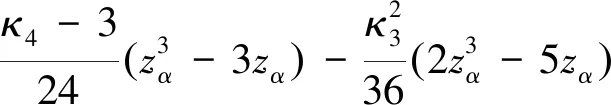
其中：zα为标准正态分布在α处的分位数；κ3和κ4分别表示偏度和峰度。在此分位数展开式之下，损失随机变量的VaR可表示为

μl和σl分别表示损失随机变量在l期内的期望和标准差。可以看出：在无法得知损失随机变量真实分布的情况下，通过样本来估计偏度κ3和峰度κ4，从而得到分位数的渐进展开值和VaR值(图2)。

1.4 基于Bootstrap抽样的VaR计算

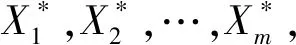
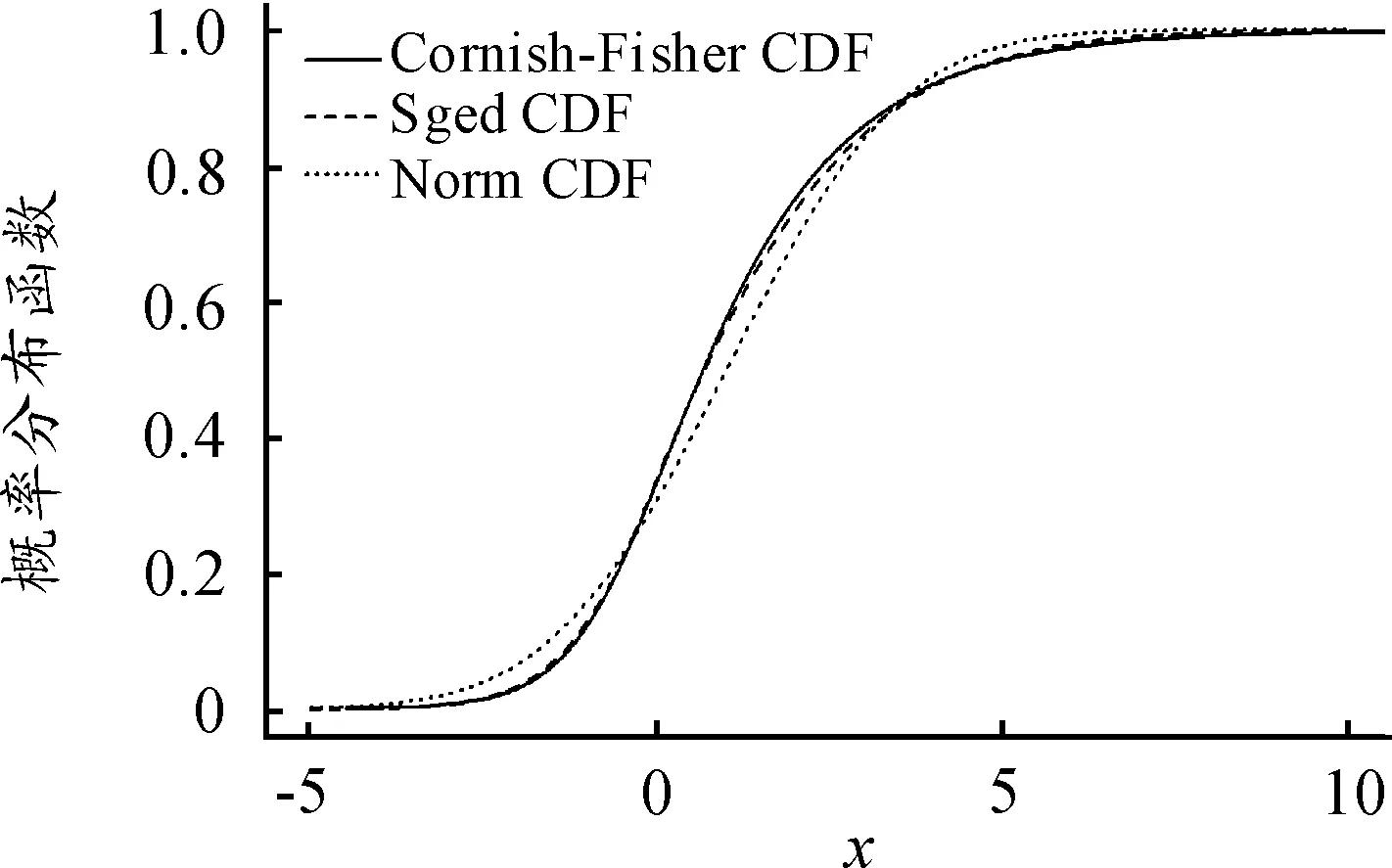
图2 均值μ=1，标准差σ=2的正态分布累积分布函数和偏度系数ξ=0.75，均值μ=1，标准差σ=2以及形状参数ν=1.5的有偏广义误差分布累积分布函数及其Cornish-Fisher展开

这里定义一种分位数的计算方法：假设x1,x2,…,xn为损失随机变量，其次序统计量为x(1),x(2),…,x(n)，那么损失随机变量的损失概率q的值近似为：

其中：l=nq；l1和l2表示与l相邻的两个整数；qi=li/n。

基于Bootstrap抽样的VaR计算的步骤为：

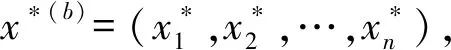
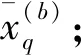
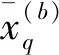
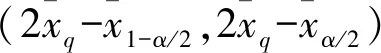
2 实证分析

本文选取苹果公司2018年3月1日到5月1日股票收盘价格Pt，共41个，进行实证分析。其中，Pt为股票在第t日的收盘价。将股票价格的对数收益率rt=log(Pt+1)-log(Pt)应用于上述的3种VaR计算方法。

如果仅从多头的角度去计算其损失的临界值，这里考虑的是收益率的负值。选取3种有偏分布来拟合负收益率数据，即有偏正态分布SN(μ,σ2,ξ)、有偏广义误差分布SGED(μ,σ2,ν,ξ)和有偏学生t分布SSTD(μ,σ2,ν,ξ)，见表1，有偏分布拟合的密度函数见图3，不同损失概率下VaR估计和95%的Bootstrap置信区间见表2。

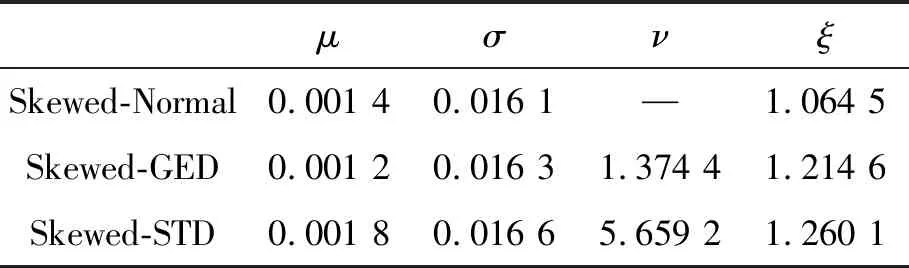
表1 3种有偏分布的参数估计

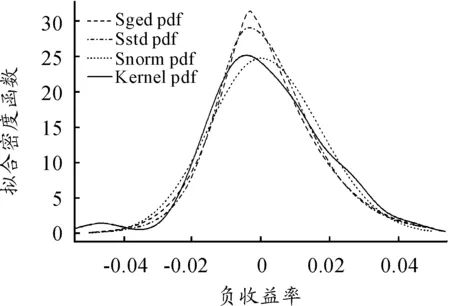
图3 负收益率数据的拟合核密度函数图及其3种有偏分布拟合的密度函数

图4为负收益率数据累积分布函数的核拟合、Cornish-Fisher近似以及3种有偏分布拟合累积分布函数。从图4可以看出：随着尾部概率的增大，Cornish-Fisher近似的累积分布函数与核拟合分布函数非常接近。若以Bootstrap方法的结果作为参照，从表2的结果可以看出：当损失概率较大时，Cornish-VaR表现较差，而基于有偏分布拟合的VaR估计与Bootstrap-VaR的绝对误差相对较小；但随着损失概率的减小，Cornish-VaR估计与Bootstrap-VaR的绝对误差逐渐变小，基于分布拟合的VaR估计与Bootstrap-VaR的绝对误差却在增加，而且一些值也已经超出了95%的Bootstrap置信区间。

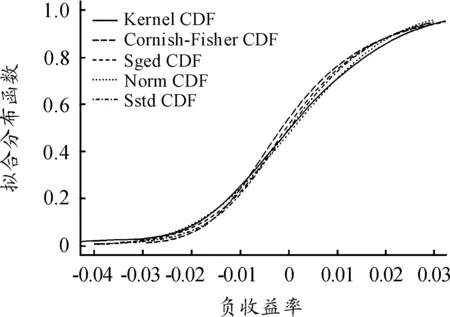
图4 负收益率数据累积分布函数的核拟合、Cornish-Fisher近似以及3种有偏分布拟合的累积分布函数

表2 不同损失概率下VaR估计和95%的Bootstrap置信区间

3 结束语

本文运用3种方法估计了小样本情况下收益率数据的VaR值。实证分析结果表明：对于小样本的收益率数据，以Bootstrap方法所得的VaR值作为参照，在一个较小的损失概率下，基于有偏分布拟合计算出的VaR值误差较大，而Cornish-Fisher方法所得的VaR值则表现得更为精确和稳定。同时，Cornish-Fisher方法不需要对分布进行假定，仅用到数据的前4阶矩，因此这种方法可以较理想地为人们提供一种可行的风险度量工具。