一种改进型隧道爆破模拟方法及其验证分析

罗 驰， 杨新安， 罗都颢， 张海清

(1. 同济大学 道路与交通工程教育部重点实验室， 上海 201804；2. 同济大学 交通运输工程学院， 上海 201804； 3. 中铁五局集团第四工程有限责任公司， 广东 韶关 512031；4. 中国地质大学(北京) 工程技术学院， 北京 100083)

爆破引起周围介质及临近建(构)筑物产生强烈的振动，可能导致邻近隧道结构损坏及地表建筑物开裂甚至倒塌，直接关系施工安全，因此，预测及分析爆破振动影响一直都是重要的理论和工程问题[1-3]。

为预测及分析隧道爆破振动对邻近建(构)筑物的影响，许多学者对此开展了研究，主要有两个方面：① 利用现场爆破监测数据对爆破应力波传播规律进行分析，通过回归得到适用于具体工程的爆破振动强度计算公式，进而提出优化的爆破与开挖方案[4-6]；② 利用数值模拟，在隧道轮廓面上施加爆破荷载，通过动力计算来研究爆破动力作用对邻近建(构)筑物的影响[7-12]。前者爆破振动预测公式的建立是以获取大量监测数据为前提的，并不能做到真正意义上的事先预测；而后者在隧道爆破模拟过程中，往往将爆破荷载过于简化，未能真实反映现场爆破实际状况，从而降低预测隧道爆破振动的准确度。

具体来说，在隧道爆破模拟方面，由于隧道爆破的炮孔数多、段别数多以及隧道尺寸与炮孔尺寸悬殊(尺寸相差2～3个数量级)，因此常用的隧道爆破模拟不单独对每个炮孔划分网格，而是根据爆破荷载模型计算得到爆破荷载，再将爆破荷载施加在隧道开挖轮廓面上。目前的隧道爆破模拟多假设爆破荷载为均布荷载，无法反映实际爆破方案中多个炮孔同时起爆及炮孔所在的不同位置的影响；并且，计算爆破荷载从炮孔传递至隧道开挖轮廓面上的应力衰减往往按单一应力衰减指数来考虑，没有考虑应力衰减指数在爆破应力波传播过程中的变化及其影响。

爆破荷载模型主要有三角波形、指数型、谐波函数型等多种形式，目前还没有统一的处理方法[13]。本文基于三角波爆破荷载模型，从考虑多炮孔爆破荷载的叠加作用以及考虑不同区域的爆破应力波衰减分析这两方面对其进行改进，使爆破模拟尽可能地接近工程实际。结合京张高铁大跨过渡段第一步爆破振动监测，将实测数据与模拟结果进行对比，验证该改进的数值模拟方法的正确性。

1 改进型隧道爆破模拟方法

本文主要从以下两方面对三角波形爆破荷载模型在隧道爆破模拟中的应用进行了改进：一方面改进了爆破应力波传播衰减分析，将应力波传播衰减从各区域应力衰减指数相同改进为不同爆破区域的应力衰减指数不同，以使其更加贴近实际；另一方面，更重要的是，考虑多炮孔爆破时每个炮孔位置不同所产生的影响，将同段别起爆的爆破荷载从均布在隧道开挖轮廓面上改进为各个炮孔爆破荷载的叠加，这就使得隧道开挖轮廓面上的爆破荷载与其空间位置及时间均相关。

1.1 三角波形爆破荷载模型概述

三角波形爆破荷载模型，假定每一段爆破时，荷载从零开始线性加载至峰值，然后再线性衰减至零。三角波型爆破荷载时程曲线，可由峰值荷载pm、起始加载时刻t0、加载时间以及卸载时间这四个指标完全确定，如图1所示。三角波形荷载典型的加载时间为8～12 ms，卸载时间约为50～120 ms。

对于不耦合装药结构的单个炮孔，其爆破引起的岩石中应力波压力计算公式为[13-14]

图1 三角波形爆破荷载示意图

Fig.1 Triangular waveform blasting load curve

(1)

(2)

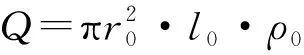
1.2 考虑不同区域下爆破应力波衰减的改进

目前，在隧道爆破的模拟中，爆破应力波衰减均按照单一的应力衰减指数进行取值，一般取为2-μ/(1-μ)，μ为动泊松比。而爆破应力波在实际传播中，随着能量的逐步衰减而形成三个区域，各个区域的应力衰减指数均不同。因此，拟先分析各个爆破区域的应力衰减指数，再建立不同区域的爆破应力波衰减函数。

在爆破应力波的传播过程中，引起的岩体中应力波能量将随远离爆源而衰减，波形也将相应地发生变化，大体可分为三个作用区[14-15]：冲击波区、压缩波区和地震波区，分别对应着爆破中的粉碎区、裂隙区以及弹性区。

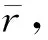
为考虑不同区域的爆破应力波衰减影响，在上述应力衰减指数及规律的基础上考虑区域交界点处数值的连续性，选取如下的应力求解公式来近似计算不同区域、不同距离的应力数值

p=p(pm,r)=

(3)

式中，R1、R2为爆破的粉碎区和裂隙区半径。

由式(3)可知，为保证粉碎区及裂隙区边缘处岩石受到的爆破应力恰好分别为岩石动态抗压及抗拉强度，粉碎区和裂隙区半径应由下式来确定

(4)

(5)

式中，Rcd、Rtd为岩石动态抗压强度和岩石动态抗拉强度。

1.3 考虑多炮孔爆破荷载叠加的改进

隧道爆破中，为控制爆破振动影响，雷管按不同延迟时间分段别进行起爆，每个段别同时起爆多个炮孔。目前在爆破模拟时，或将同时起爆的多个炮孔按集中爆破进行近似，或对周边孔爆破计算等效荷载施加在炮孔联心线上，但都没有真正考虑多炮孔爆破荷载叠加引起的荷载空间分布特征及其影响。

为考虑爆破设计方案中所有炮孔的影响，需计算所有段别每个炮孔产生的爆破应力波传递至隧道轮廓面上的应力荷载，再对隧道轮廓面上各点求出该段别所有炮孔爆破传递过来的应力的合应力，最终将该合应力施加在隧道轮廓面上。

具体叠加思路如下：在爆破开挖掌子面处建立如图2所示坐标系，x、y、z方向分别为隧道横向、纵向及竖向，对应爆破振动的径向、切向与垂向。考虑一般用于隧道爆破的炸药均为柱状装药，长细比较大，爆破荷载也以XOZ面内荷载为主，故在计算各个炮孔传递至隧道轮廓面上的爆破荷载时按平面应变问题来考虑，研究y=y0截面。

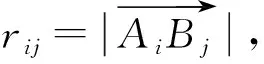
假定同段别所有炮孔同时起爆，则Ai炮孔处产生的爆破应力波传播至隧道爆破轮廓面Bj处的传播时间tij=rij/c，式中c为该岩体纵波传播速度。

(6)

采用同样的方法，求得各段别、隧道轮廓面各位置点处各时刻的爆破荷载，再对各段别爆破引起的爆破动荷载同样进行矢量叠加，就能求得各位置在各时刻的爆破荷载。最后，在模拟计算时将该爆破动荷载施加至隧道轮廓面处。

图2 多炮孔爆破荷载叠加示意图

2 八达岭长城站爆破现场实测

为验证该改进型隧道爆破模拟方法的正确性，结合八达岭长城站隧道爆破工程，监测其大跨过渡段第一步爆破开挖时在8号分通道迎爆侧的爆破振速，并与改进型爆破模拟结果进行对比。

2.1 八达岭长城站爆破工程概况

京张高铁是国家规划实施的重点建设项目，也是2022年北京张家口联合举办奥运会的配套工程。京张高铁八达岭长城站是目前国内埋深最大的暗挖高铁地下车站，位于八达岭长城景区之下和新八达岭隧道之中。

现场监测的京张高铁八达岭长城站大跨过渡段第一步爆破里程为DK68+386～DK68+ 398，围岩为弱风化斑状二长花岗岩，围岩级别为Ⅲ级。大跨过渡段是八达岭长城站与八达岭隧道间的过渡区域，为一段变截面的隧道，爆破监测里程位置跨度为24.69 m，分11步进行开挖，首先挖通第一步以探明地质情况。第一步断面宽8 m、高6.5 m，循环进尺为3 m，其炮孔布置如图3所示，炮孔孔径为42 mm，爆破炸药采用Φ32 mm岩石乳化炸药。爆破雷管采用不耦合装药，分1/3/5/7/9/11段依次爆破，各段别炮孔的相关参数如表1所示，总药量为120 kg。

图3 炮孔布置图(mm)

表1 爆破装药参数

1.2 爆破实测数据分析

已建成的8号分通道与该大跨过渡段第一步保持平行，两者水平间距31 m，高差为6 m，在8号分通道迎爆测的拱腰及拱脚处监测大跨过渡段第一步爆破的振速。两隧道的相对位置及监测点布置如图4所示，采用TC-4850爆破测振仪进行监测。

图4 爆破振速监测点布置图(mm)

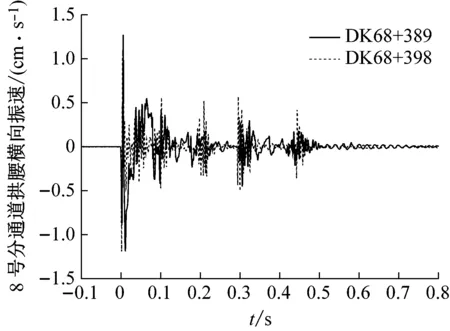
现场监测共在8号分通道处测得4次爆破振速数据，其大跨第一步爆破开挖里程分别为DK68+386、DK68+389、DK68+395以及DK68+398，其监测振速数据如表2所示。

表2 爆破监测最大振速值

由于距离较远，拱脚振速与拱腰振速相差已不大；振速方向以径向振速为主，其次是垂向、切向振速最低，径向振速大致为0.7～1.2 cm/s，垂向振速大致为0.6～0.7 cm/s，这主要是由监测点的8号分通道与爆破点的大跨过渡段第一步的相对位置所决定的。

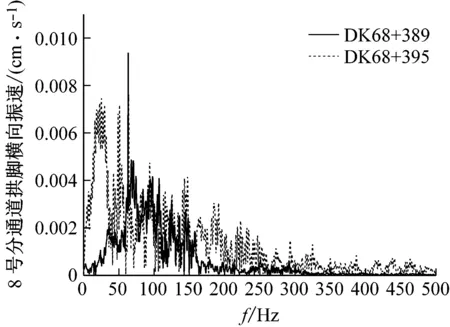
现场监测得到的爆破峰值最大振速均为径向振速，以拱脚及拱腰径向振速为例，其爆破振速时程曲线如图5所示。爆破振速出现6个振速峰值，与6段炸药是相吻合的，并且最大爆破振速出现在第1段的掏槽眼。对爆破监测振速时程曲线进行FFT变换，得到其频谱如图6所示，该监测得到的爆破振速主频以50～100 Hz为主。

3 八达岭长城站爆破模拟及验证

3.1 模型建立及模拟过程

采用FLAC3D中对大跨过渡段第一步开挖爆破进行数值模拟，建立大跨第一步隧道及8号分通道模型如图7所示，计算尺寸为：隧道横向范围取-50～50 m，隧道纵向取90 m，隧道竖向从-140 m至地表0 m。

为模拟现场真实情况，模拟计算按如下过程进行：① 先一次性挖通8号分通道并施做C30喷射混凝土初期支护，计算在岩体自重下的静应力，即为大跨第一步隧道未开挖前的初始应力场；② 按3 m的循环进尺开始逐步开挖大跨第一步隧道，施做C30喷射混凝土初期支护并对模型进行静力计算，如此循环开挖直至接近隧道爆破研究里程；③ 开挖隧道爆破处的岩体，在开挖轮廓面上施加爆破动荷载并进行动力计算，监测其在8号分通道处产生的振速大小，如图8所示。

(a) 拱脚径向振速

(b) 拱腰径向振速

(a) 拱脚径向振速

(b) 拱腰径向振速

图7 计算模型图

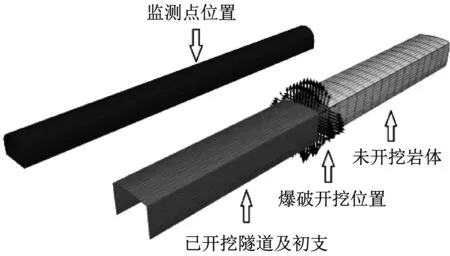
图8 爆破模拟示意图

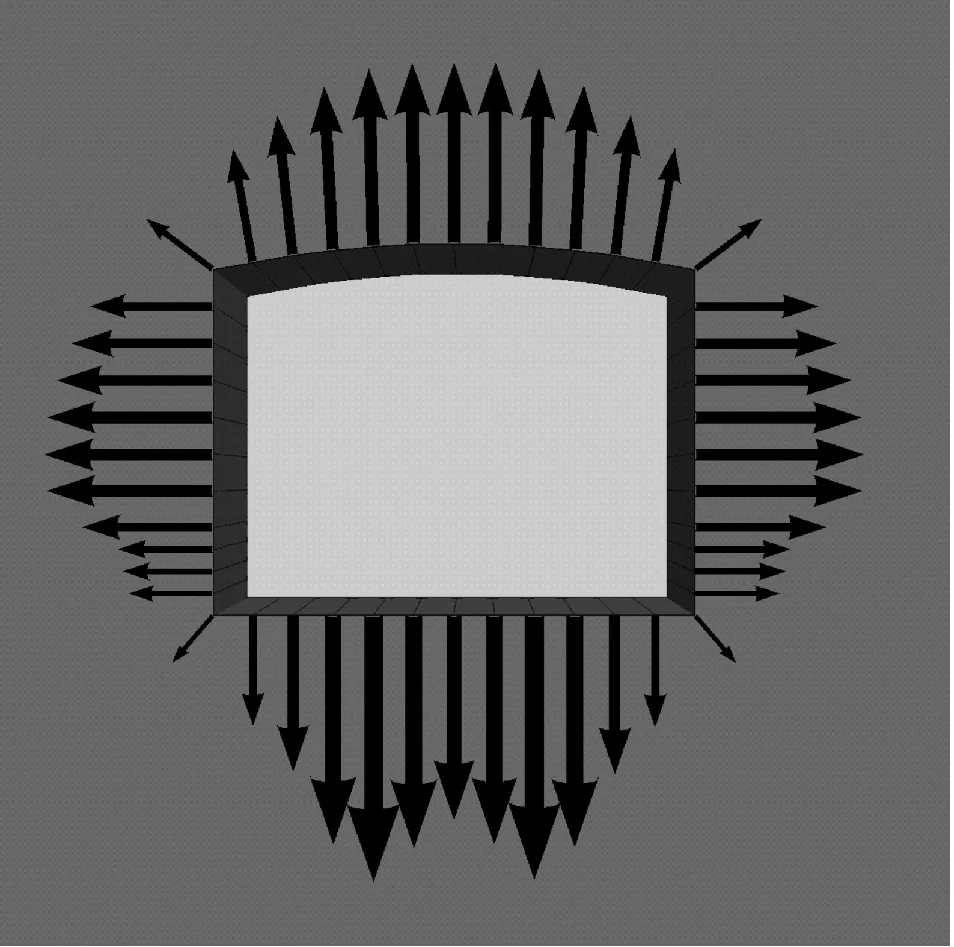
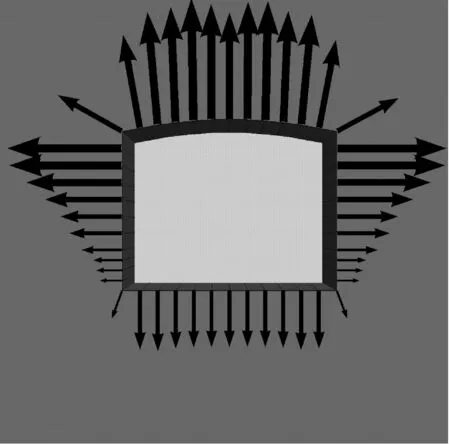
爆破动荷载按照改进型隧道爆破模拟方法进行计算，将最终叠加得到的荷载施加至隧道开挖轮廓面(沿纵向长度按循环进尺取为3 m)上，该荷载在开挖轮廓面处不同位置或不同时刻均不相同：从荷载空间分布来看，隧道开挖轮廓面处的叠加荷载在10、60、120、210、320及470 ms时的荷载分布如图9所示，其中10 ms为三角波爆破模型的加载时间；从时间上来看，以开挖轮廓面右下角处点B为例(见图4)，其爆破荷载时程曲线如图10所示。

边界条件：静力学计算时，模型上方边界自由，模型前后、左右及下方边界均为位移约束边界，约束垂直该边界面方向上的位移；动力学计算时，模型上方边界采用自由边界条件，模型前后、左右及下方边界采用黏性边界条件，能吸收边界处的入射波。

3.2 计算参数的选取

3.2.1 围岩及支护动力学参数

国内不少学者采用回归分析研究围岩静力参数与动力参数之间的关系，王思敬等建立了动弹性模量Ed与静弹性模量Es的转换计算公式[16]

(7)

在工程爆破的加载频率范围内，戴俊建立了动泊松比μd与静泊松比μs的转换计算公式[17]

(a) 10 ms

(b) 60 ms

(c) 120 ms

(d) 210 ms

图10 B点处爆破荷载时程图

μd=0.8μs

(8)

围岩采用摩尔库伦本构模型模拟，其静力学参数根据Ⅲ级围岩进行取值。C30喷射混凝土采用shell单元模拟，厚0.1 m，其静力学参数根据C30混凝土进行取值。结合式(7)、(8)可计算出相应动力学参数，各参数如表3所示。

在岩体的阻尼方面，实用动力分析和应用最为广泛的是瑞利阻尼，它将整体阻尼矩阵[C]由整体质量矩阵[M]和整体刚度矩阵[K]的线性组合来表示，即

[C]=α[M]+β[K]

(9)

式中，比例系数α和β可由式(10)确定

表3 围岩及支护参数计算表

(10)

式中，ωmin为最小中心频率，Hz，它与所研究体系的固有频率以及输入荷载频率均有关；ξmin为最小临界阻尼比，它与岩体材料性质等有关。

本模拟中，围岩瑞利阻尼的最小中心频率按爆破的平均频率取值，取为50 Hz；最小临界阻尼比取0.5%。

3.2.2 爆破荷载计算参数

在爆破三角波峰值荷载计算参数的选择方面，三角波加载时间取10 ms、卸载时间取100 ms，炸药爆速取4 000 m/s，药卷半径及炮孔半径分别取21 mm和16 mm，装药长度与炮孔长度认为相等，其他各个物理量均按照表1所示取值。

在爆破应力波衰减方面，需要确定该围岩的动态抗压及抗拉强度。岩石的动态抗压强度随加载率的增大而增大，一般来说，对于岩石爆破可近似地用下式统一表达岩石动态抗压强度与静态抗压强度的关系

(11)

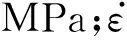
该计算中，根据室内岩块试验，静态抗压强度为60 MPa，而爆破产生的应变率取50 s-1，则岩石动态抗压强度由式(11)计算为221 MPa。岩石的动态抗拉强度随加载应变率的变化很小，在岩石爆破时可按静态抗拉强度计算，故岩石动态抗拉强度可取2.1 MPa。

在多炮孔荷载叠加上，各个炮孔的爆破参数按表1进行计算，而炮孔位置则如图3所示，此外，岩体纵波速度选取为5 200 m/s。在计算时，考虑到周边孔实际工程施工中按照距爆破开挖轮廓线10 cm处向外打孔，故模拟时也对周边孔位置进行了相应调整。

3.3 模拟结果与实测数据对比

数值模拟得到的8号分通道迎爆测处拱脚及拱腰径向振速模拟结果与实测数据对比如图11所示，其各段别峰值对比如表4所示。从中可以看出，拱脚及拱腰爆破径向振速模拟结果的最大峰值分别为0.824 cm/s和1.124 cm/s，均在在0.7～1.2 cm/s范围内，1#爆破实测拱脚与4#爆破实测拱腰径向振速的最大峰值分别为0.637 cm/s和1.192 cm/s，模拟与实测结果相差不大；振速波形及各段别峰值也基本一致。经过FFT变化，其振速频谱如图12所示，主频均为77.1Hz，在50～100 Hz范围内，与爆破实测的主频范围基本一致。

(a) 拱脚振速

(b) 拱腰振速

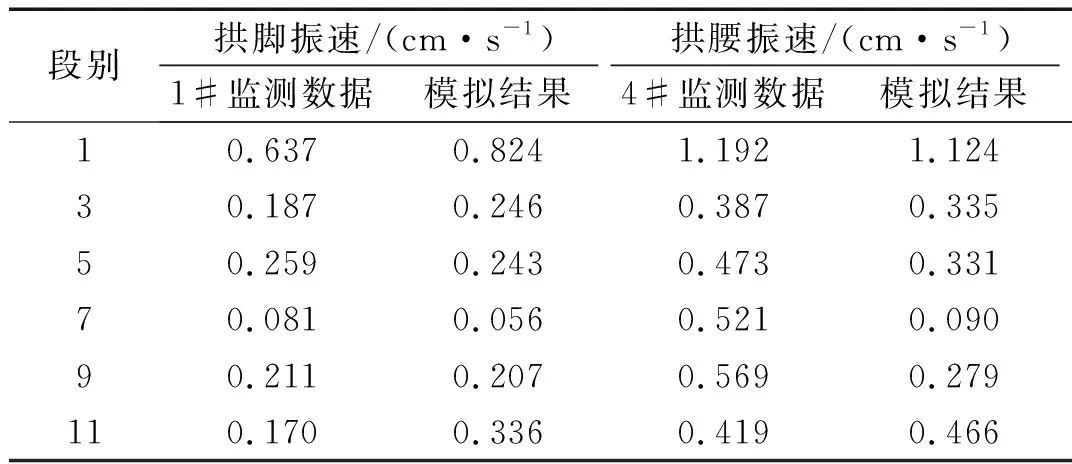
段别拱脚振速/(cm·s-1)拱腰振速/(cm·s-1)1#监测数据模拟结果4#监测数据模拟结果10.6370.8241.1921.12430.1870.2460.3870.33550.2590.2430.4730.33170.0810.0560.5210.09090.2110.2070.5690.279110.1700.3360.4190.466

图12 径向振速频谱模拟结果

综上，通过对比爆破振速模拟结果及实测数据，两者较为吻合，说明改进型隧道爆破模拟方法能较好地反映爆破振动的影响，并可采用本文提出的爆破模拟计算方法对爆破振速进行预测。

4 结 论

(1) 本文从隧道爆破中多炮孔同时起爆的特点出发，基于三角波爆破荷载模型而提出改进型隧道爆破模拟方法，使爆破模拟尽可能贴近实际。主要改进以下两个方面：① 考虑隧道爆破多炮孔的影响，基于炮孔的实际布置和爆破应力波传播情况，计算隧道开挖轮廓面处叠加的爆破荷载并施加至模型中；② 考虑爆破应力波在冲击波区、压缩波区和地震波区的不同应力衰减指数，改进近似求解不同距离处爆破应力波的计算公式。

(2) 现场实测京张高铁八达岭长城站大跨过渡段第一步爆破开挖时在8号分通道迎爆侧的爆破振速，从方向上看，实测爆破振速方向以径向振速为主，而切向振速最小，径向振速大致为0.7～1.2 cm/s，垂向振速为0.6～0.7 cm/s；从峰值上看，爆破振速最大峰值均出现在第1段的掏槽眼时；从振动频率上看，振动主频以50～100 Hz为主。

(3) 采用改进型隧道爆破模拟方法对大跨过渡段第一步爆破开挖进行数值模拟，该方法计算并施加在隧道开挖轮廓面上的爆破荷载与其空间位置及时间均相关。数值模拟得到8号分通道迎爆侧拱脚及拱腰爆破径向振速最大峰值分别为0.824 cm/s和1.124 cm/s，其振速主频为77.1 Hz，与实测结果基本一致；改进型隧道爆破模拟方法能较好地预测和分析爆破振动的影响。

致谢

由衷感谢中铁五局的科技部肖承倚副部长、京张项目部蒋思总经理和李坤对本文研究的协助与配合，以及中国矿业大学(北京)为本文提供的八达岭长城站大跨过渡段第一步爆破振速实测数据。