基于时频分析的高温振动环境螺栓连接件松动判别

曹芝腑， 谭志勇， 姜 东， 何顶顶， 费庆国

(1.东南大学 空天机械动力学研究所,南京 211189； 2.东南大学 工程力学系,南京 210096；3.北京临近空间飞行器系统工程研究所,北京 100076； 4.南京林业大学 机械电子工程学院,南京 210037)

航空航天、能源等诸多领域由于其高温高压及强振动的严苛工作环境[1]，需要连接结构在此环境下仍能保持足够的刚度、强度、稳定性及耐久性，传统材料很难满足这些要求。因此复合材料由于其比重小、高温环境下比刚度高、比强度大及服役寿命久等诸多优点，得到越来越多国内外工程研究人员的广泛重视和研究，并在相关领域得到广泛使用和发展[2-5]。随着复合材料在工程中的广泛应用，复合材料结构设计越来越复杂，加之由于成型工艺水平、设计和使用维护等方面的限制，工程中往往需要将复合材料结构件用连接技术连为整体，复合材料结构的连接问题不可避免。对于复合材料连接结构设计，连接部位是一个相对薄弱的环节，结构的连接破坏是导致结构失效的主要原因之一，尤其是某些重要连接部位的失效破坏，有可能会危及整体结构的安全性和可靠性。

复合材料结构的连接形式主要有3种[6]：胶接连接、机械连接和混合连接。机械连接有螺栓连接、销钉连接和铆钉连接等方式，其中螺栓连接具有可靠性高、承载能力强、便于重复拆装及使用维护简便等优点[7]，是航空航天领域中复合材料结构的主要机械连接方式。基于复合材料螺栓连接的优点和存在的缺点，有必要对其连接特性进行深入分析，改善不利因素的影响，提高连接效率[8]。

松动失效是最常见的连接结构失效模式，近年来有不少国内外学者致力于连接结构松动诱致失效、故障的研究。研究主要分为两方面，一方面建立连接结构松动动力学模型，分析连接结构松动对系统动力学特性的影响[9-10]；另一方面是基于结构动响应分析的方法[11-12]，利用动力学实验中结构非线性动响应，结合非线性动力学理论提取描述结构松动状态的特征参数，建立结构松动状态与非线性特征参量之间的关系，进行连接结构松动状态监测和辨识。

Lü等[13]通过试验建立螺栓残余应力与温度和初始预载荷之间的关系，对复合材料-复合材料，复合材料-金属和金属-金属等不同形式连接结构的松动行为进行分析。该方法能够利用短期试验数据构造半解析的时间-温度相关蠕变率方程，并利用该方程对螺栓连接结构的预紧力松弛现象进行长期预测。赵登峰等[14]建立了螺纹连接松动高度简化的动力学模型，通过数值仿真和实验相结合的方法，研究了振动环境中螺栓连接松动过程的动响应特性，提出将谐波失真度作为螺栓连接松动失效的预警指标。Li等[15]针对具有螺栓松动特征的卫星结构，在有限传感器的条件下，利用二阶频谱对其松动故障进行识别。Nguyen等[16]利用结构健康监测的方法，利用不同螺栓松动工况下的振动响应数据，对风力发电机塔结构进行螺栓松动损伤识别。Amerini等[17]使用健康监测系统研究了螺栓结构在松动和收紧状态时连接结构接触面的线性及非线性声学参数，使用一阶声学矩作为螺栓松紧状态的指数，这一方法能够有效评估螺栓连接的健康状态。另外，研究了单频和多频激励下，高次谐波产生及边带调制的非线性方法，其中在单频激励下，结构信号的二次谐波幅值与载体信号的基频振幅的比值可以作为一个可靠的指标，有效评估螺栓的装配状态。

本文进行了高温振动环境下复合材料连接件螺栓松动试验研究，并使用短时傅里叶变换的时频分析技术对高温振动响应进行分析，得到了复合材料连接结构在各试验条件下的时频结果。采用二倍频与基频振动对应的幅值比作为松动特征值，对复合材料螺栓连接结构在高温环境下的振动松动状态进行了综合评估。

1 松动特征量

图1所示为螺栓连接件结构，在高温环境下，结构除产生x方向伸缩变形外，还会产生z向变形。同时由于螺栓的约束和接触面的粗糙[18]，使得结构连接区域的相互接触刚度具有非线性特性。一种可行的处理方案是将连接位置的非线性接触关系简化为非线性集中力[19]，利用非线性弹簧进行简化建模，如图2所示。

考虑如图2所示的均质等截面简化梁模型，其在位移为z(t)的基础振动下的动力学微分方程为

(1)

式中:w为悬臂梁挠度，由线性项wlin和非线性项wnlin组合而成，即w(x,t)=wlin(x,t)+wnlin(x,t)，E为弹性模量，I为梁横截面惯性矩，ρ为密度，S为横截面积，δ(x,l)为狄拉克函数，fnl为非线性集中恢复力，z(t)为基础振动位移。针对均质等截面梁，ρS为常数，则式(1)可简化为

(2)

式中:FNL表示t时刻的等效非线性载荷，

(3)

其中k1和k2为由于温度变化引起的螺栓连接界面处的一次和二次刚度系数，是温度T的函数k1=f(T)，k2=g(T)。

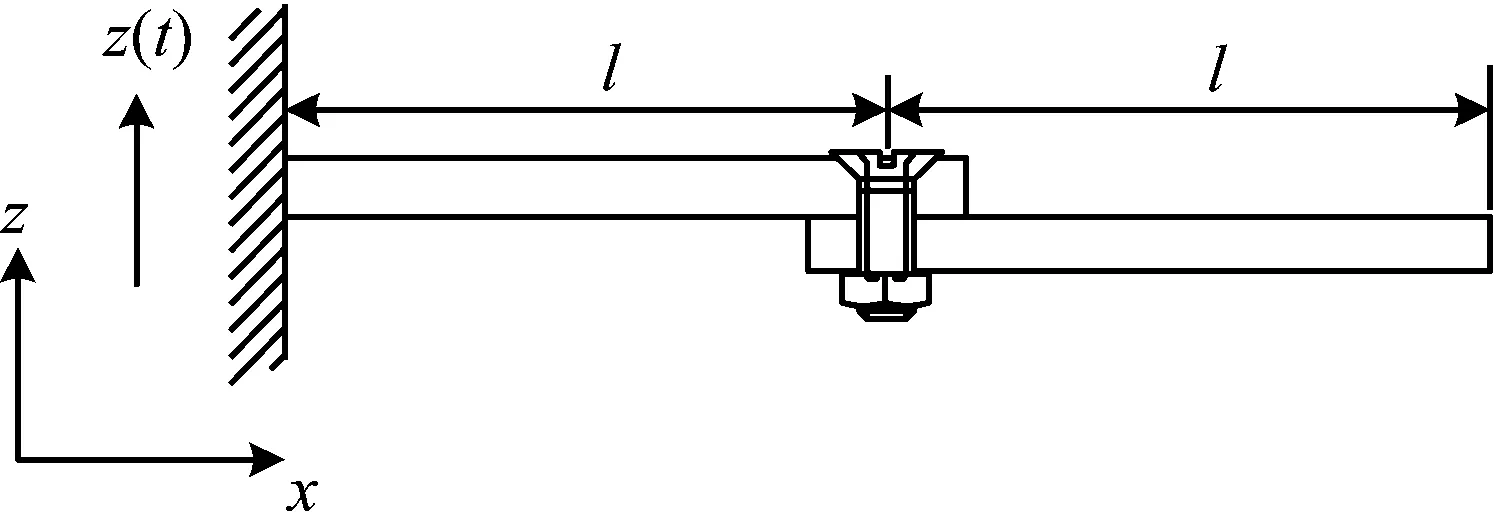
图1 螺栓连接结构

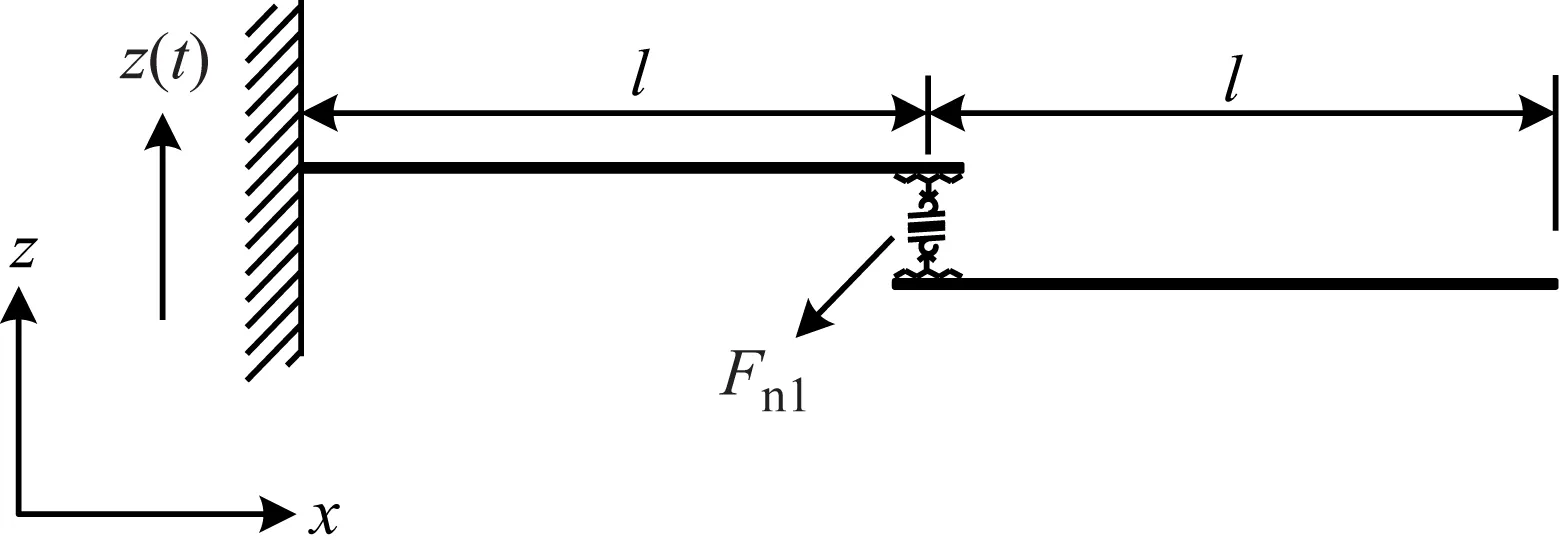
图2 等效非线性弹簧-梁模型

文献[20]指出在该等效建模前提下，结构的非线性动响应包含二次谐波项。在频域下，定义无量纲量r(Z)为二次谐波幅值与基频幅值的比，作为螺栓连接结构的松动特征指标，对松动特性进行评判

(4)

式中，Z为振动幅值(加速度，速度，位移)。

2 时频域分析松动判别

时频域分析方法是非平稳信号处理的一个重要分支，它是利用时间和频率的联合函数来表示非平稳信号，并对其进行分析和处理。时频分析的主要任务是描述信号的频谱含量随时间的变化规律。时频分析的最终目的是建立一种分布，以便在时间和频率上同时表示信号的能量或强度，得到这种规律后，就可以对连接结构振动信号进行分析和处理，从而提取信号中所包含的特征信息。

傅里叶变换难以反映信号频率成分的时间特性。但是，如果沿着时间轴把信号在时域上加以分段，每一段作傅里叶变换，计算其频率，则可以从各段频谱特性随时间变化上看出信号的时变特性。这就是目前在时变信号分析中广泛使用的分析方法：短时傅里叶变换，因其处理过程简单、高效，得到了广泛的研究和使用。

短时傅里叶变换[21]的概念最早由Gabor于1946年提出的，其计算公式为

(5)

式中：h*(τ-t)是滑移时窗h(τ-t)的共轭，滑移时窗用来对信号进行分段截取。

3 试验研究

3.1 试验件

图3和图4分别是复合材料螺栓连接组件的几何尺寸和实物图，由同种复合材料板通过复合材料螺栓进行连接，构成复合材料螺栓连接试验件。

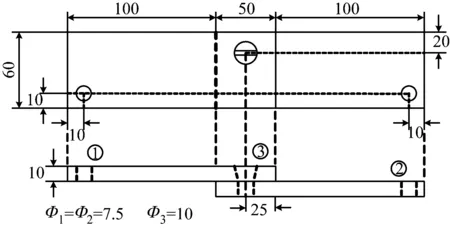
图3 复合材料螺栓连接组件几何结构(mm)

图4 复合材料螺栓搭接板

3.2 试验系统

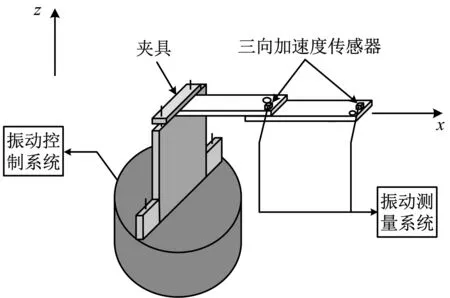
高温振动试验系统示意图和装置图如图 5所示，常温振动试验系统示意图如图6(a)所示。常温试验系统主要包括振动控制系统和接触式振动测量系统，高温试验系统主要包括振动控制系统、温度控制系统和非接触式振动测量系统。其中：

振动控制系统主要装置为电动振动台(型号：D-600-5；频率范围：5～3 000 Hz；额定加速度：100g)；

温度控制系统由1 000 ℃高温环境箱(控制精度±1 ℃)及双铂铑型(K型)热电偶(测温精度±1.5 ℃)组成；

振动测量系统由德国Micro-Epsilon公司的ODC-1200-10光幕式激光位移传感器及基于Labview的非接触式激光振动实时测量软件组成。针对常温振动试验，采用接触式测量方法，如图6(b)所示。其中传感器为三向加速度传感器，型号为LC0122C-50；频率范围：1～4 kHz；量程：50g；灵敏度：6.05 pC/g。

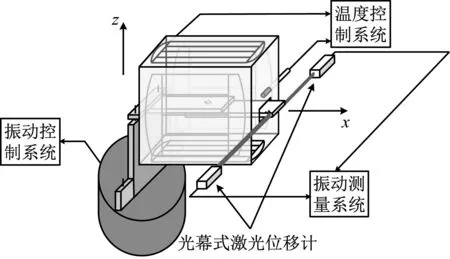
(a) 高温振动试验系统

(b) 试验系统布置

夹具如图6(b)左端所示，该夹具利用4根不锈钢丝杆配合夹块紧固，夹块材料为45号钢。为保证夹持力均匀一致，对夹紧螺母施加相同大小的拧紧力矩。

3.3 试验流程

利用上述试验件及试验系统分别进行常温和高温环境下的振动防松试验，试验流程图如图3所示。常温振动防松试验流程为：常温环境下，首先对试件进行扫频试验和分析，得到分析结果S1；然后进行结构振动试验(5 min低量级，3 min高量级，15 min低量级)，并在每次振动试验结束后对构件进行扫频试验和分析，得到分析结果S3，S4，S5。

(a) 振动试验系统

(b) 传感器布置

与常温振动防松试验相比，高温振动防松试验在整个流程中会利用温度控制系统对试件进行加热，调控试件在振动过程中的环境温度。针对高温振动防松试验，增加高温和冷却至常温后的扫频试验步骤，得到分析结果S2和S6。结构振动试验(5 min低量级，3 min高量级，15 min低量级)及后续的扫频试验均在高温环境下进行，即图7中虚线框部分。低量级和高量级的载荷谱分别如图8和图9所示。扫频试验中的扫频速

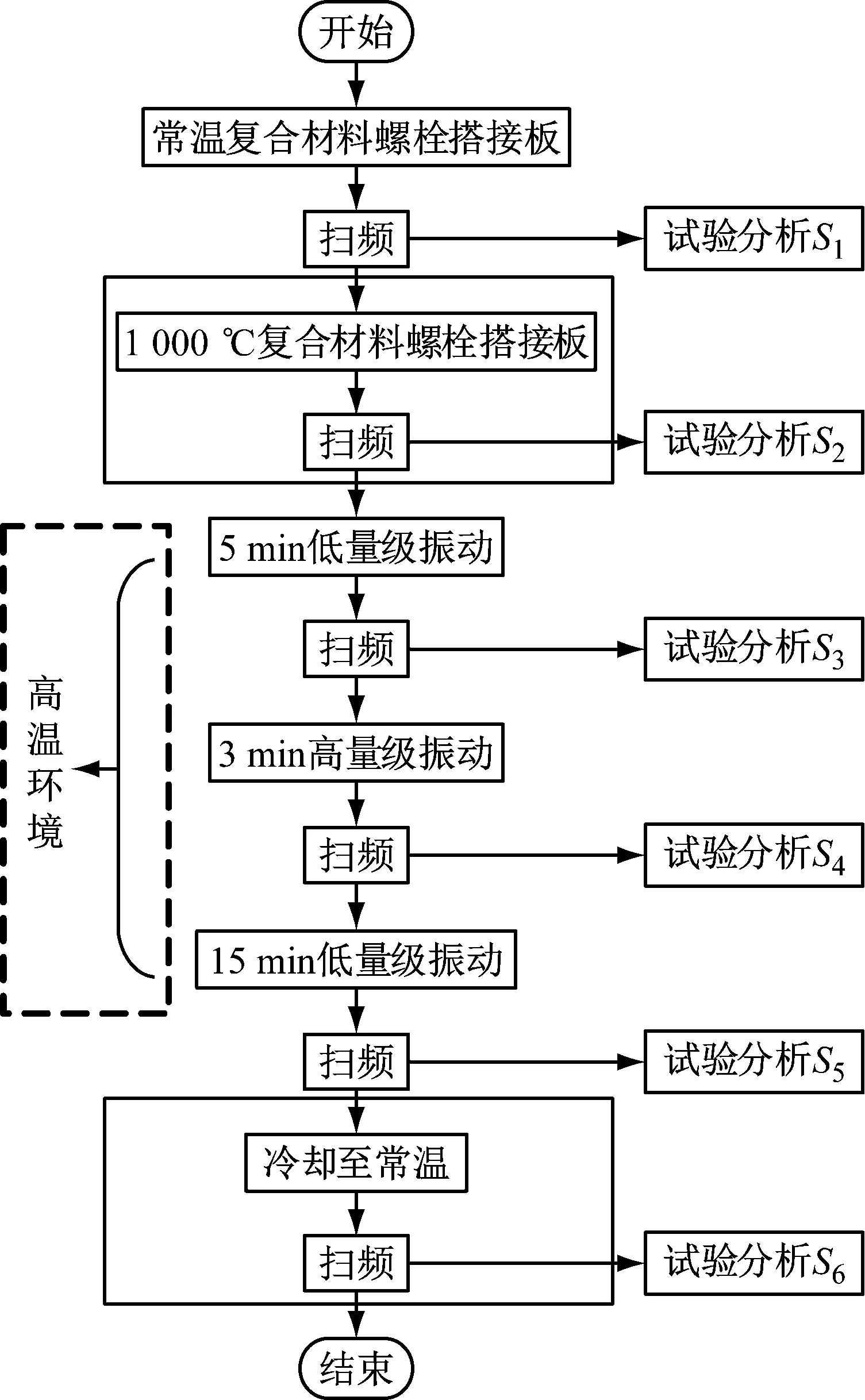
图7 常/高温振动试验流程图

图8 低量级载荷谱(Grms=4.7g)

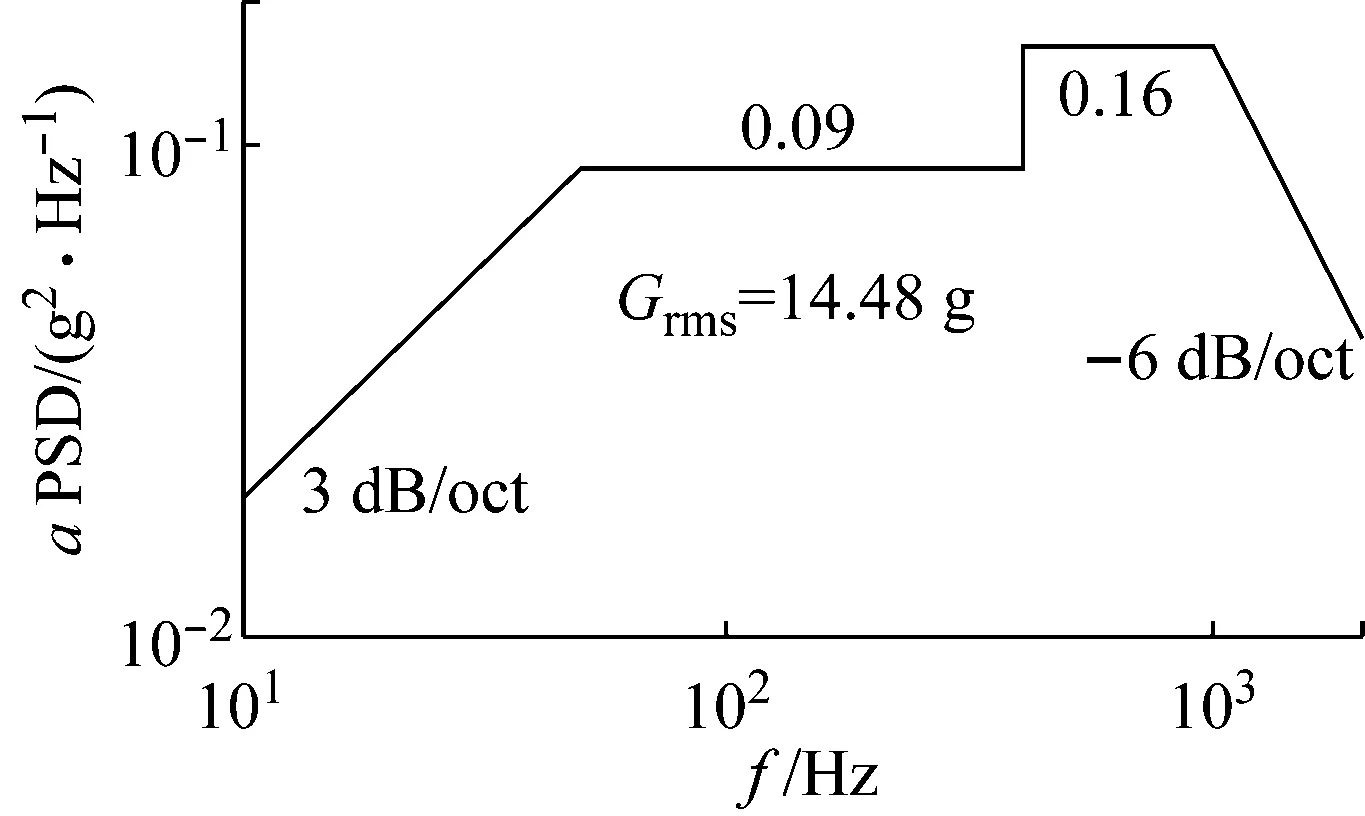
图9 高量级载荷谱(Grms=14.48g)

度为0.1 OCT/min，扫频中振动台加速度值恒定为0.5g。

4 试验结果与分析

按图7所示试验流程完成高温振动试验，利用非接触式振动测量系统获取响应数据。但由于工频成分的存在，影响试验结果的分析。本文利用一维数字滤波方法，滤除工频和倍频干扰对试验的影响

a1y(N)=b1x(N)+b2x(N-1)+…+bnb+1x(N-nb)-

a2y(N-1)-…-ana+1y(N-na)

(6)

式中:x为输入响应，y为输出响应，ai和bj分别为滤波系数，na和nb分别为反馈滤波器和前馈滤波器阶数。为了实现对工频干扰信号的滤除，采用二阶数字滤波器来消除工频响应。滤波系数向量a和b分别为[1, -2cosω0, 1]和[1, -2rcosω0,r2]。其中ω0=2πf0/fs，f0为滤波频率，fs为采样频率，r为常数，取0.9。

图10 滤波前S2时频分析结果

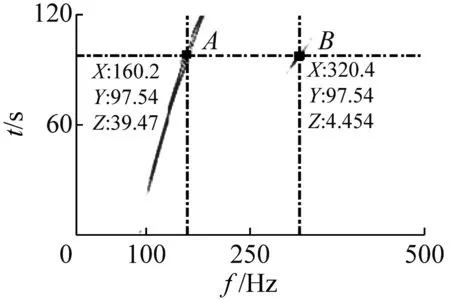
利用短时傅里叶变换时频分析技术对试验结果进行分析，得到高温振动环境下各试验流程中的时频图，如图11所示。图11中Z值最大的点(图11(a)～图11(f)中的A点)即为结构振动基频的振动振幅。然后选取二倍频所对应的B点，利用式(4)计算得到松动特征指标计算结果:r(Z)=ZB(2ωn)/ZA(ωn)。常高温环境下，扫频振动后计算得到的松动特征指标结果如图12所示。

(a) S1

(d) S4

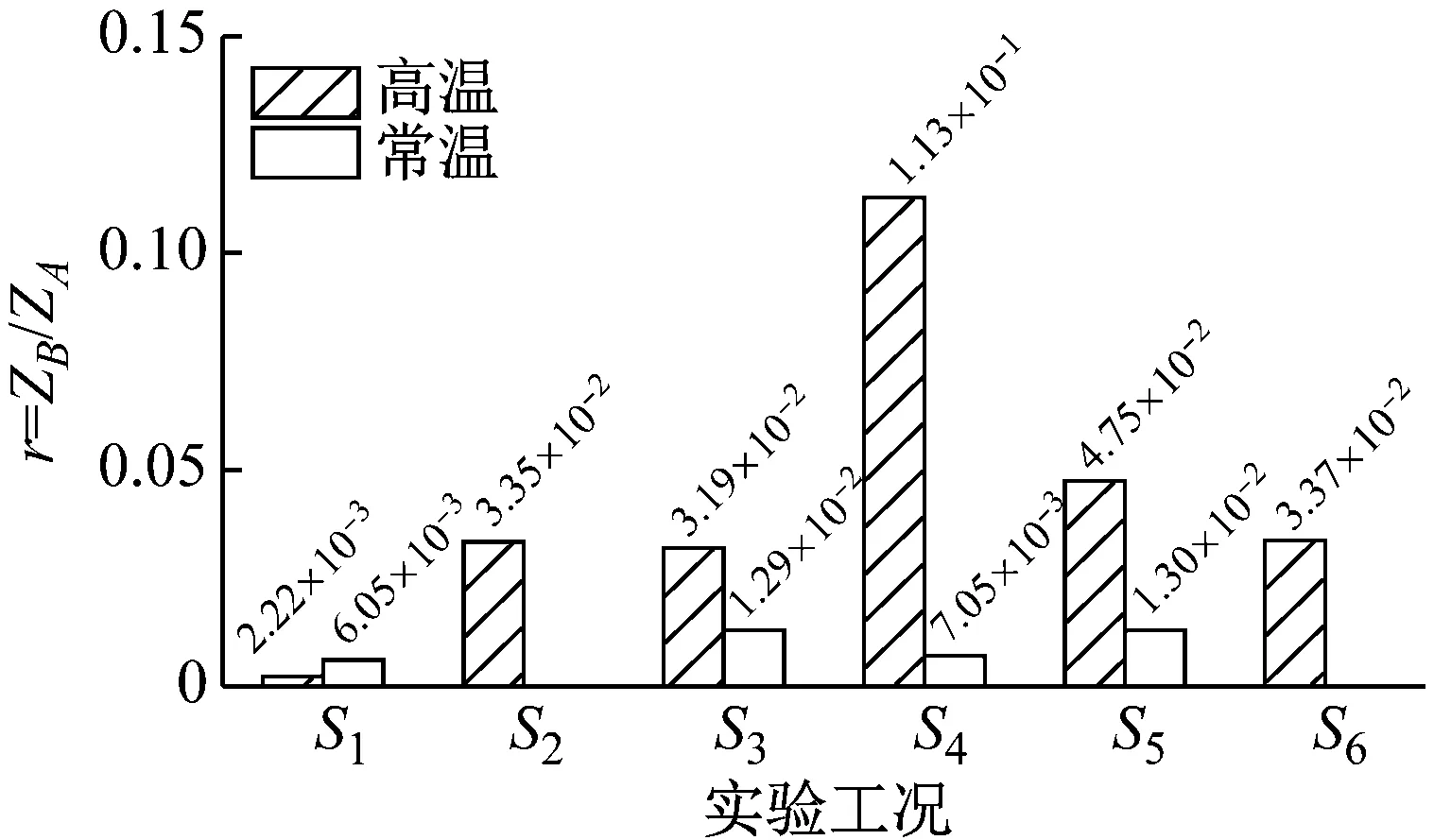
图12 常温和高温下各扫频试验后松动指标对比图

(1) 图11(a)对应于试验流程中常温环境下扫频振动后的分析结果S1。从图中可以看出，二倍频成分不明显。结合图 12可知，其初始松动判别指标为6.05×10-3，结构在常温状态下未出现连接松动。

(2) 随着温度的升高，结构振动基频增加，且螺栓连接处接触状态发生改变，导致图11(b)呈现多频成分，松动特征值量级增加，综合判定连接结构在1 000 ℃高温环境中开始出现松动迹象。

(3) 图11(c)～图11(e)分别为1 000 ℃高温环境下，5分钟低量级，3分钟高量级和15分钟低量级振动后的扫频试验结果。从图中可以看出，松动特征值在3分钟高量级振动后达到最大，是常温状态下松动特征值的50.9倍。且图中二倍频成分均能清晰显现，说明连接件在高温振动环境下松动特征明显。

(4) 图13所示为试验前、后螺栓连接局部对比图，在恢复到室温后，连接件未见明显变形。图11(f)为试验件恢复到常温后扫频试验分析结果S6，与试验前比较，二倍频成分明显。图12所示，在高温环境下，S6对应的松动特征指标为3.37×10-2，为高温初始状态的15.18倍。而常温振动环境下，S5对应的松动指标为1.3×10-2，为常温初始状态的2.15倍。比较可知，高温振动环境下，连接结构更容易产生松动。

(a) 试验前

5 结 论

本文针对某型复合材料螺栓连接结构进行不同量级下的高温振动防松试验，利用时频分析方法提取振动特征响应，通过定义的高温松动判别指标r(Z)，实现了高温振动环境下复合材料螺栓连接结构的松动特性判别及分析。

(1) 时频分析能够清晰表明复合材料螺栓连接件在试验过程中的频率成分及变化，为特征响应提取提供准确的分析结果。

(2) 结合基频变化，二倍频振幅和二倍频与基频的振动幅值比值作为松动特性评判的特征量，能够有效评判复合材料螺栓连接结构在常/高温环境下的振动松动特性。

(3) 高温对连接件结构材料属性的影响，振动对连接处接触状态的改变，会导致连接结构在高温振动后更容易出现连接组件的松动。