固支薄膜结构强非线性振动解析方法研究

李英民， 宋维举， 王肖巍

(重庆大学 土木工程学院，重庆 400045)

薄膜结构由于造型美观自由、透光、节能等优势，被广泛应用于建筑小品或者大跨空间屋盖结构。但由于其高柔度、低自重，因而对外荷载的作用非常敏感，容易发生振动[1]，一般情况下薄膜结构在振动过程中的横向振幅较大，表现出较强的非线性状态[2-3]。大幅振动导致的膜结构破坏案例较多，因此，研究薄膜结构的振动性能，把握振动规律以及影响因素，对其设计、施工以及日常使用都具有重要意义[4]。针对薄膜结构非线性自振特性解析研究，已有一些研究成果，林文静等[5]基于小挠度理论给出了圆形薄膜自由振动的理论解；潘钧俊等[6]根据达朗贝尔原理建立了方形膜结构的离散非线性振动方程组，推导了结构在一阶振型初始位移下的等效一阶频率的计算公式；刘长江等[7]采用KBM法对矩形膜结构有阻尼自由振动进行求解，得到了振动频率和位移函数的近似解析式。上述方法基本都是基于小挠度理论或者弱非线性摄动方法对薄膜振动进行解析研究，忽略了薄膜结构强非线性的振动特性。

本文通过理论和试验方法研究平坦矩形正交异性薄膜结构四边固支条件下的强非线性振动特性，运用改进多重尺度法结合Galerkin法从理论上求解平坦张拉膜结构非线性振动方程，得到薄膜结构强非线性振动频率及位移的近似解析函数，给出了不同振型下薄膜自振频率随初始条件的变化关系。借鉴“弹射法”测量膜结构预张力的试验方案[8]进行膜材自振试验研究，通过试验验证了改进多重尺度法的适用性，为膜结构强非线性动力解析研究提供了理论基础。

1 平坦薄膜强非线性振动理论推导

1.1 控制方程和边界条件

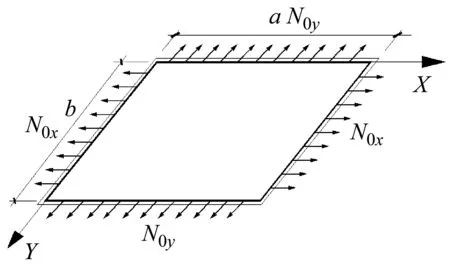
假设平坦薄膜沿x轴方向边长为a，沿y轴方向的边长为b，如图1(a)所示。

假定薄膜结构在水平位置处于静止平衡状态，给膜面施加初始法向位移使其连续振动，如图1(b)所示。文献[3]给出了正交异性薄膜非线性自由振动的控制方程组

(1)

(2)

式中:ρ表示膜材面密度；c表示阻尼系数；σ0x表示x向预应力；σ0y表示y向预应力；w表示w(x,y,t)横向振动挠度；h表示薄膜厚度；E1表示x向弹性模量；E2表示y向弹性模量；φ表示应力函数。

(a)

(b)

相应的边界条件为

(3)

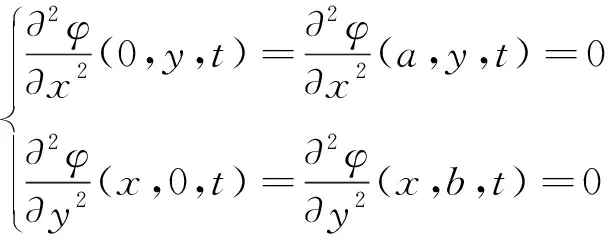
(4)

假设满足边界条件的位移函数和应力函数为

(5)

(6)

式中:φmn(x,y)、Tmn(t)为未知函数。

最终，通过参数代换和Galerkin法可以得到一个非线性偏微分方程。

(7)

1.2 控制方程的改进多尺度解

根据摄动法的基本思想，

(8)

将建筑工程膜材参数代入ε可估算出ε>>1，则式(8)为强非线性振动微分方程。

引入变换参数[9]

(9)

将ω2展开为ε的幂级数

(10)

(11)

式(8)的摄动解形式为

T(t,α)=T0(t0,t1)+αT1(t0,t1)+

α2T2(t0,t1)+…

(12)

式中:t0=t,t1=αt

关于t的导数化成关于Tn的偏导数的展开式，即有

(13)

将式(9)、(11)和(13)代入式(8)，并令方程式中α的各幂次的系数为零，可得：

(14)

(15)

(16)

设式(14)解可写成

(17)

将式(17)代入(15)，消除永年项可得

(18)

求解式(18)可得：

(19)

令A=feiφ/2，代入式(20)并分离虚部和实部得

(20)

式中:f为平坦薄膜振动幅值。

比较式(20)得角频率和式(11)可知一阶近似条件下

(21)

比较式(20)和(21)即可得到ω1的表达式，ω1=3f2/4ω0，将其代入式(10)并略去高阶项得

(22)

(23)

(24)

积分式(24)可得

(25)

式中:f0为与初始条件有关的积分常数。因此可得式(8)的一阶摄动解为

(26)

式中:f0和φ0由初始条件确定。给定任意振动初始条件

(27)

式中:T0为初始位移。

对式(26)求一阶导并将初始条件带入即可得到

(28)

求解式(28)可以得到f0和φ0的值。

(29)

将式(29)代入式(5)，得到考虑振动阻尼的平坦矩形薄膜结构强非线性振动位移函数

(30)

根据式(30)可以计算出薄膜结构膜面任意一点的位移时程。

1.3 数值算例

以建筑工程领域常用的织物膜材为例，取ρ=1.2 kg/m2;a=1.2 m;b=1.2 m;c=90 N·s/m3;h=1.0 mm;E1=1.4×106kN/m2;E2=0.9×106 kN/m。

将式(22)结果与文献[7]KBM摄动解及文献[10]精确级数解进行对比，分析振动频率随初始位移T0的变化关系，见图2。

由图2可知当初始位移较小时，改进多尺度解和KBM摄动解及精确级数解基本吻合，随着初始位移的增大，系统表现出较强的非线性，KBM解与精确级数解的相对差值变大，改进多尺度法依然能很好的与级数解相吻合，证明改进多重尺度法对于薄膜结构强非线性振动系统的适用性较好。

图3是采用改进多尺度法计算的各阶振动振幅的变化趋势三维图，从图3可知，随着振动阶数的增加振幅是减小的，从最大幅值分布三维图形可以看出，当为验证理论方法的有效性，参考已有“弹射法”测量建筑膜结构预张力试验编制了张拉膜结构振动特性试验方案[11]。

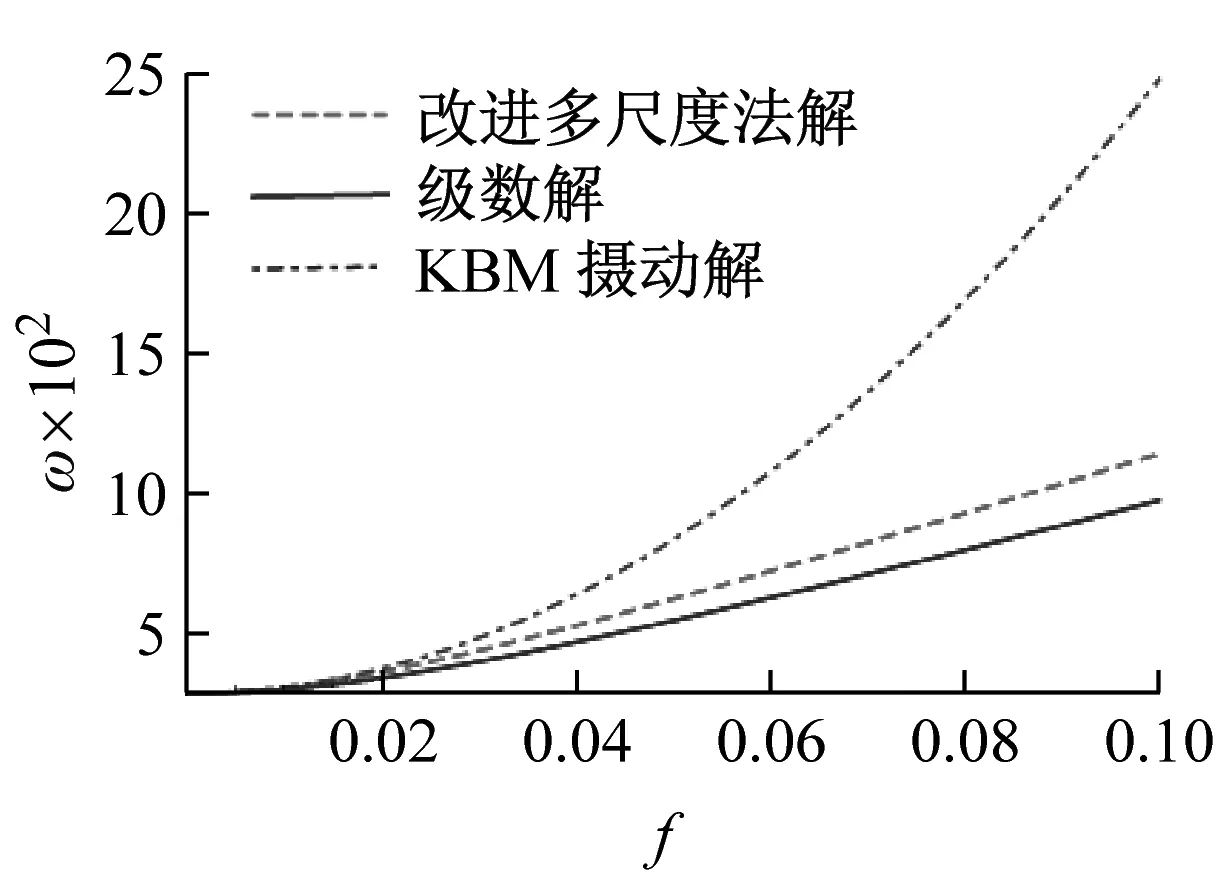
图2 振动频率随振幅变化曲线

Fig.2 Amplitude-frequency response curve

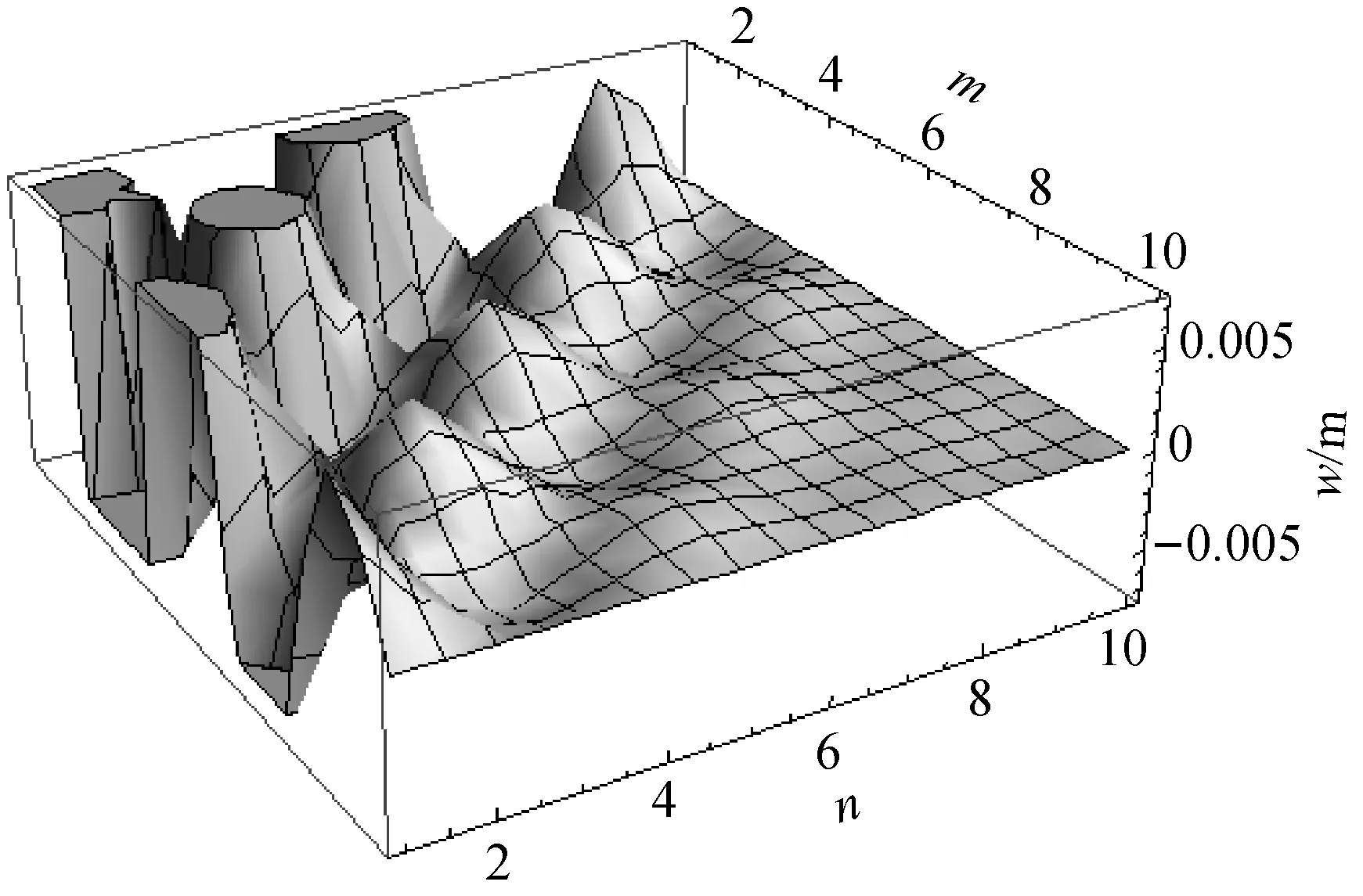
图3 各阶振动振幅变化趋势图

m>5,n>5时，振动幅值基本已经接近于零，即薄膜的振动响应主要聚集在低阶振型，高阶振型贡献很小。

2 平坦薄膜振动试验研究

由于膜材试件数量所限，本试验主要针对不同预张力下的薄膜振动响应进行研究，其它因素如膜材厚度，膜材尺寸等对薄膜振动响应的影响分析将后续开展。

2.1 试验试件

试验选用正方形国产ZZF膜材试件，膜材的密度为950 g/m2；厚度为0.72 mm；径向弹性模量为1 590 MPa；纬向弹性模量为1 360 MPa；正向拉伸强度为4 000 N/5 cm；反向拉伸强度为3 700 N/5 cm。试件几何边长为2.5 m，四端进行带宽为100 mm的切缝处理，膜材试件四角处分别裁掉边长为650 mm的小正方形，然后对四边做直径400 mm倒圆角处理，处理后膜材四边进行锁边和钻螺栓连接孔，膜面设置三个测点，具体图示见图4。

2.2 张拉与测量装置

采用改进的“十字形螺杆式膜材张拉装置”，其平面尺寸设计为3 800 mm×4 160 mm，中心正方形区域为1 200 mm×1 200 mm，其高度为1 600 mm，整个试验支架和斜撑用60 mm×60 mm的方钢管焊接而成，用M20螺杆进行张拉。为模拟理论推导时四边固支边界条件。张拉装置中心正方形区域设置试验架，试验架对边均匀对称布设4个螺栓孔，由试验架上四个螺栓在膜面下方托起方形铁框(尺寸为1 200 mm×1 200 mm)，膜面上方设置相同尺寸方形铁框，使其与膜面下方的方形铁框完全重合，在膜面上方的方形框之上压重铁块，使膜面上下方形框夹紧膜材，即可得到四边近似固支的矩形膜材测量区域。

试验测量装置主要包括测力计与位移传感器。试验选用HP-10K数显式推拉力计置放于张拉螺杆与薄膜夹板之间，进行膜材张拉力的测定。采用英国激光距离传感器ZLDS100来测量膜面的振动，具体布置见图5。

图5 张拉与测量装置布置图

2.3 加载方案

试验中，采取分级张拉形式，张拉时薄膜x，y方向的拉力值相等，预张力级别分别为1.0 kN、2.0 kN、3.0 kN、4.0 kN、5.0 kN、6.0 kN、7.0 kN、8.0 kN。每一预张力级别下，用鼓风机通过送风装置竖向对膜面进行瞬间冲击后立刻关闭风机，以此模拟膜面自由振动初始能量输入。用数字风速计测得接近膜面的风速平均值为11.2 m/s，为减小试验误差，每一预张力工况，风机进行重复冲击数次。最终初始位移和最大振幅均取数次平均值。送风装置见图6。

图6 送风装置

3 试验结果及验证分析

以风机瞬时冲击膜面产生的变形为初始位移，带入理论计算式，分别求解平坦薄膜振动基频与最大振幅，由于风力较小，施加给膜材的初始能量较小，作用时间短，很难激发起膜材的高阶振动，因此在进行幅值计算时只考虑前两阶振型。图7是ZZF膜材试件的三个测点处振动幅值与振动频率的理论计算和试验数据对比图。由图7可知，理论计算与试验结果相对误差较小。理论计算所得幅值和频率均大于试验结果，原因是理论计算中的振型函数来源于板壳理论，振型函数与实际振动状态相比偏饱满，造成理论计算时膜面刚度偏大，此外薄膜是一种柔性材料，简单的振型函数不能精确的反映实际复杂的振动情形，所以频率与振幅都较试验值偏大。

(a) C1测点

4 结 论

通过对平坦张拉膜结构自由振动的理论和试验研究，主要得出以下结论：

(1) 采用改进多重尺度法得到的平坦薄膜自振频率与振幅响应与精确级数解接近，随着初始位移的增加，薄膜振动表现出较强的几何非线性，改进多重尺度法相比传统KBM摄动法而言，其适用性不受初始位移的限制。

(2) 借鉴板壳理论选取振型函数研究柔性膜结构的振动会存在一定的误差，简单的三角振型函数不能精确的反映薄膜实际的振动情形，由于假设的振型函数偏于饱满，导致理论计算刚度偏大，所以理论值存在偏大的情况。

(3) 本文的理论工作为后续研究张拉膜结构风致动力灾变问题提供了一定的理论基础，并且通过试验结果对比得到理论推导过程中由于简化计算而导致的误差原因，后续理论研究中可采取更为准确的振型函数来描述膜结构的振动形态。