大跨度铁路斜拉桥全桥索-梁相关振动研究

王 涛， 刘德贵， 黄 辉

(西南科技大学 土木工程与建筑学院，四川 绵阳 621000)

斜拉索是斜拉桥的主要受力构件之一，桥面重量及桥面上荷载大部分通过拉索传递到桥塔。斜拉索具有刚度小、阻尼小、质量小的特点，容易在各种激励下发生振动。关于拉索各种类型振动的性质与理论分析方法等，可以参考文献[1]。

斜拉桥在风或车辆荷载作用下，桥面会发生一定幅度的振动，拉索端点的位移激励会带动拉索发生振动，斜拉索受到的端点位移激励分量通常包括沿拉索横向的强迫激励与沿拉索轴向的参数激励，其中，强迫激励可能导致拉索发1∶1主共振，参数激励可能导致拉索发生2∶1参数共振(1∶1与2∶1为端点位移激励达到的频率值与拉索自振频率值的比例)。 文献[2]中将斜拉桥中拉索在端点位移激励下发生的振动命名为“索-梁相关振动”。

Fujino等[3]首次观察到了日本一座人行斜拉桥上索-梁相关振动导致的2∶1参数共振，结合观察到的实际现象建立了简化索-梁组合结构的理论模型与实验模型，研究了拉索在端点位移激励下，面内与面外振动。陈水生等[4-5]在他们的研究中建立了拉索在端点位移激励下非线性振动理论模型、拉索-质量块耦合非线性振动模型，考虑了索的垂度、几何非线性、拉索桥面端点位移激励等因素，推导了斜拉索的在端点位移激励作用下的非线性振动方程；使用理论方法结合数值分析，详细地研究了斜拉索的在端点位移激励下的强迫振动与参数振动特性。

陈丕华等[6]通过实验模型研究了斜拉索在平面内的参数振动特性。赵跃宇等[7]使用理论方法建立了索-梁组合结构的简化理论模型，讨论了简化索-梁组合结构中拉索发生索-梁相关振动的共振稳定性。王志骞等[8]分析了索-梁组合结构理论模型的非线性振动性质并研究了其振动控制措施。

康厚军等[9]收集了前期各个学者的研究资料，总结了目前关于斜拉桥拉索在端点位移激励下非线性振动研究的现状。依据现有的研究成果可以发现，对于斜拉桥的索-梁相关振动，目前已有的研究中普遍使用单索、索-质量块或简化的索-梁组合结构理论模型来开展研究，取得了较多的理论性成果。但由于斜拉桥全桥为多根拉索与梁的组合，发生索-梁相关振动时拉索与梁、塔振动相互作用的机理更为复杂(如：多索与梁、塔相互动力作用，索与相邻索的动力作用等等)，因此，理论模型几乎无法开展斜拉桥全桥尺度下发生索-梁相关振动时拉索的非线性振动研究。

Caetano等[10-11]以韩国Jindo大桥(主跨343 m)为研究对象，通过理论分析、数值计算、模型振动台实验，研究了斜拉桥的索-梁相关振动现象。Calcada等[12]在葡萄牙Salgueiro Maia大桥(主跨246 m)上进行现场测试，研究了重载汽车通过时主梁与拉索的振动情况。孙测世等[13]建立了象山港大桥(公路斜拉桥，主跨688 m)的全桥缩尺实验模型，分析了斜拉桥在模拟外激励各种工况下的索-梁相关振动的特性。

全桥模型实验往往只能针对某个特定的桥梁研究，而实桥测试由于研究经费、实桥运营等因素的限制，测试工况往往难以达到要求，难以得到较为明确的研究结果。使用精细的数值计算来模拟研究斜拉桥全桥的索-梁相关振动不存在上述问题。因此，文献[9]也指出，由于技术手段的限制，前期关于斜拉桥全桥在索-梁相关振动作用下的非线性振动研究成果相对较少，目前需要进一步结合数值计算技术发展，开发斜拉桥全桥计算系统，建立计算模型，深入探讨各种桥型、各种工况下，索-梁相关振动导致的拉索非线性振动特性。

翟婉明等[14]详细研究了列车-桥梁耦合动力作用下，桥梁结构以及车辆的振动响应。但目前车-桥耦合振动主要关注的是桥梁结构动力响应的评价，没有重点分析列车动力作用导致的索-梁相关振动对拉索的影响。雷虎军等[15]开发了车桥耦合振动算法，研究了拉索的局部振动效应，但研究中动力时程积分使用了传统的线性有限元算法，拉索的应力刚度不会随着受力的增加而变化。

本文以笔者建立的基于CR列式(Co-rotational Formulation)非线性有限元动力时程积分算法为基础，编制了非线性动力有限元计算程序(计算中使用平面杆、梁单元)，程序算法具有简洁、高效的特点[16]。笔者在文献[17]中，进一步验证了本文所使用有限元程序的正确性，并将杆、梁模型的CR列式非线性动力有限元程序应用推广到了3维空间。

在本文研究中，首先，使用2维动力非线性有限元程序研究了斜拉桥模型在简谐激励、自由振动状态下的非线性振动特性，依据前期各个学者研究得到理论原理解释了索-梁组合结构中拉索发生的1∶1主共振、2∶1参数共振、亚谐波共振等非线性振动现象。然后，使用开发的车-桥耦合振动算法，在全桥有限元模型的基础上，计算了不同工况的列车-桥梁耦合动力作用下拉索的非线性振动情况。最后研究结果表明：对于承受荷载较大的大跨度铁路斜拉桥，全桥结构刚度较大，列车导致的动力作用不容易达到索-梁相关振动的拉索共振条件(1∶1主共振或2∶1参数共振)，拉索不会发生大幅度非线性振动。文献[1，3]中的研究报道也验证了发生大幅度索-梁相关振动的桥梁往往多为小跨度、拉索与桥梁质量较小自振频率都较高的桥梁而无大跨度铁路斜拉桥。

1 计算原理

1.1 基于CR列式的非线性有限元法

基于流动坐标 的CR列式几何非线性有限元计算方法具有计算速度快、力学概念简洁的特点，通常不必计算、推导复杂的单元非线性大位移刚度矩阵，更适用于模拟柔性结构，特别是索结构的大幅度非线性振动。本文使用了2维杆、梁单元模型进行了计算。

如图1所示，按照CR列式原理，在单元上附加一流动坐标系X1Y1，坐标原点始终位于单元i节点上，X1轴始终沿单元节点ij方向，Y1轴始终垂直于X1轴。当单元节点发生位移与转角时，单元变形后流动坐标系位置由图1(a)变为图1(b)。

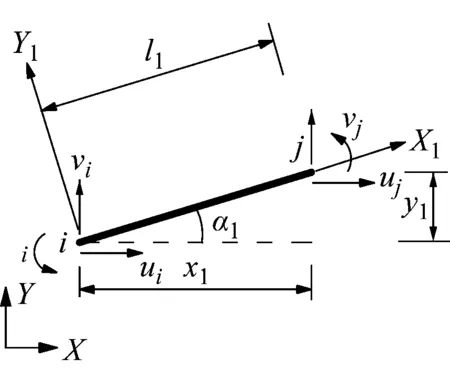
(a) 单元变形前

更新局部坐标系位置，通过坐标的变化可以计算得到单元伸长，计算扣除刚体转动，即可得到单元节点的实际转动量。杆单元为梁单元的退化情况，只需计算局部坐标系下单元伸长即可。计算得到的是单元节点“几何精确”意义的实际位移，进一步可以得到单元的实际内力。然后，计算不平衡力与切线刚度矩阵，使用Newton-Raphson 方法迭代，就能得到结构的几何非线性静力状态。

1.2 基于CR列式的非线性有限元动力时程积分

本文在CR列式的非线性静力计算的基础上，进一步开发了非线性Newmark-β有限元动力时程积分方法。其基本假定与普通的Newmark-β法相同，可以写为

(1)

(2)

其中各个积分参数的具体表达式与意义可参见文献[16]。考虑几何非线性时，结构t+Δt时刻的振动方程为

F[u(t+Δt)]+Fe[u(t+Δt)]

(3)

将式(1), (2)代入式(3)，得到：

(a0M+a1C)u(t+Δt)+R[u(t+Δt)]=

F[u(t+Δt)]+Fe[u(t+Δt)]+

(4)

由式(4)可知，非线性有限元Newmark-β动力时程积分实际上是在每一个积分时间步内求解非线性方程(4)。式(4)左端R为有限元总体节点内力向量，它是总体节点位移向量u的非线性函数，与静力计算原理相同，本文程序中使用CR列式非线性有限元计算原理来计算得到结构内力向量R。式(4)右端，F表示结构承受的总体节点外力向量，Fe表示结构初始单元力导致的等效总体节点外力向量，当计算中考虑几何非线性时，它们都是位移u的非线性函数。

使用Newton-Raphson法迭代求解式(4)。在迭代过程中使用的切线刚度矩阵为

K=a0M+a1C+KK

(5)

式中：M,C,KK分别为将节点坐标更新到当前迭代步位置上时，结构的总体质量矩阵、总体阻尼矩阵、线性静力计算时计算的总体刚度矩阵。

非线性有限元动力时程计算具体流程与算法验证可参考文献[2，16-17]。

1.3 列车-桥梁耦合振动计算模型

与文献[19]相同，如图2所示，本文高速列车使用了4轴2维列车模型。

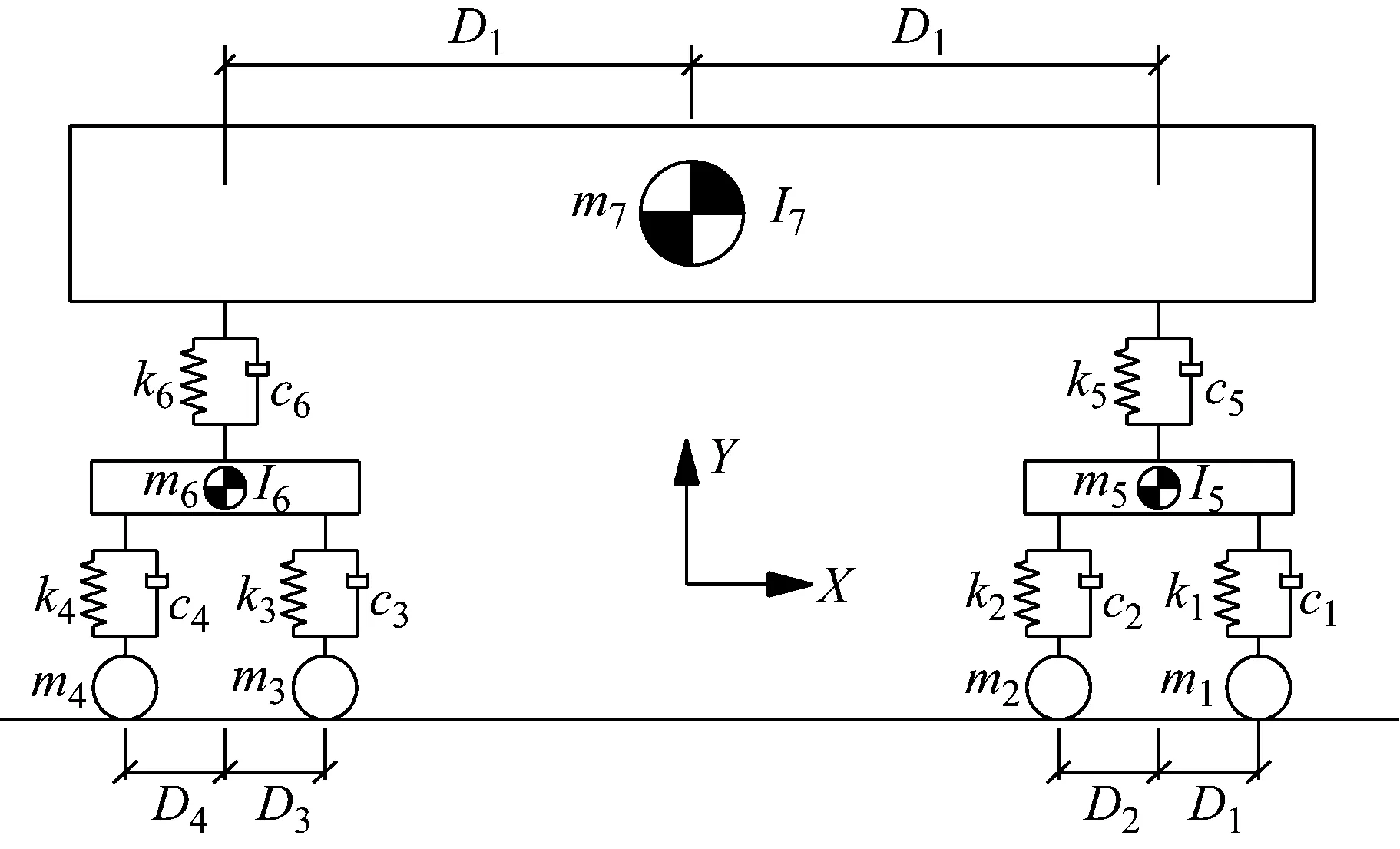
图2 一节列车车厢模型

列车的车厢的振动模型为

(6)

式中，Mv,Cv,Kv分别为列车车厢的质量矩阵、阻尼矩阵、刚度矩阵，它们的取值可以参考文献[14-15，19]。

实际计算中以标准高速客运列车动车组8节车厢编组为一辆列车，计算不同速度下列车通过桥梁的动力响应。本文算例中的铁路斜拉桥为多线铁路桥，所以程序中设计了能包含多辆列车同时(正向、逆向、不同行驶速度)过桥的计算模型。为了考虑不同列车的不同速度，程序设计中使用统一时间步长，通过计算调整时间步长使列车空间步长小于0.2 m。

轨道不平顺选用美国六级谱，计算中使用2维模型，因此只有列车沿轨道运行的高低不平顺

(7)

式中：Sv(Ω)为轨道的不平顺功率谱密度函数[cm2/(rad/m)]，Av为粗糙度常数(cm2·rad/m)；Ωc为截断频率(rad/m)；k为安全系数，可根据要求在0.25～1.0之间选取，一般取为0.25；模拟算法使用文献[14]中给出的方法，使用美国六级谱计算的轨道不平顺算例如图3所示。

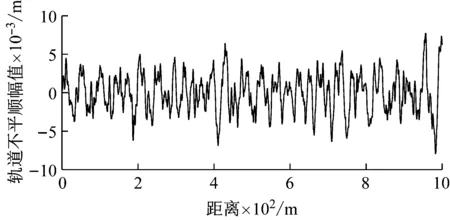
图3 美国六级谱轨道高低不平顺模拟结果

对于桥梁模型动力时程计算的阻尼，通常将结构的阻尼矩阵简化为质量矩阵[M]和刚度矩阵[K]的线性组合，即：

C=aM+bK

(8)

式中，a,b可由桥梁结构前2阶振型的阻尼比和其相应的自振频率表示

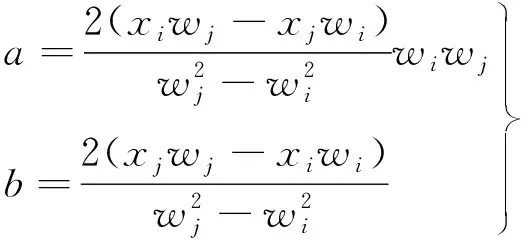
(9)

式中，wi,wj分别为第i阶和j阶振型的自振频率，xi,xj是对应的阻尼比。计算中i,j分别取1,2阶全桥整体模型的自振频率，对应阻尼比参考文献[1]中斜拉桥阻尼比建议为0.1%，为了体现更明显的振动效果，这里均取为0.05%。

综上所述，对于式(4)，式(6)给出的桥梁有限元模型非线性振动方程以及列车振动方程，本文采用与文献[14-15，19]中相同的车、桥分离迭代法求解，其一般的基本步骤为

步骤1 计算列车运行速度每一节车厢的轮对当前时间步t时刻在桥梁上的位置。

步骤2 以t-1时刻的桥梁运动状态作为初始值，叠加t时刻的轨道不平顺值，得到t时刻等效轨道不平顺。

步骤3 根据t时刻轨道不平顺求车辆轮轨力。

步骤4 使用线性Newmark-β法计算t时刻车辆响应。

步骤5 使用本文非线性Newmark-β法计算t时刻桥梁响应。

步骤6 根据t时刻桥梁响应，重复步骤2～步骤6，直到轮轨和桥梁的振动几何、力学关系满足要求(一般迭代3次即可达到收敛条件)，再进行下一时间迭代。

2 斜拉桥全桥索-梁相关振动特性研究

本文研究使用作者开发的基于CR列式动力非线性有限元程序(使用2维杆、梁单元)建立了斜拉桥全桥计算模型。

2.1 全桥有限元模型

本文选取有代表性的武汉天兴洲公铁两用大跨度斜拉桥为研究对象，认为列车为大桥的主要动力荷载，所以计算中只考虑了列车作用。建立简化的2维有限元全桥模型研究全桥结构发生竖向振动时，拉索在端点位移激励下发生索-梁相关振动时的振动特性。

实际斜拉桥的横向刚度较大，实际运营中列车作用下斜拉桥发生的振动主要是竖向平面内振动，所以，本文模型应当是合理的。关于天兴洲大桥的各个计算参数以及结构构造可以参考文献[20]。

天兴洲大桥全长1 092 m，主跨540 m。为双塔三索面三主桁斜拉桥，拉索最长为271.8 m，最短为88.9 m。使用本文程序建立的全桥有限元模型如图4所示。

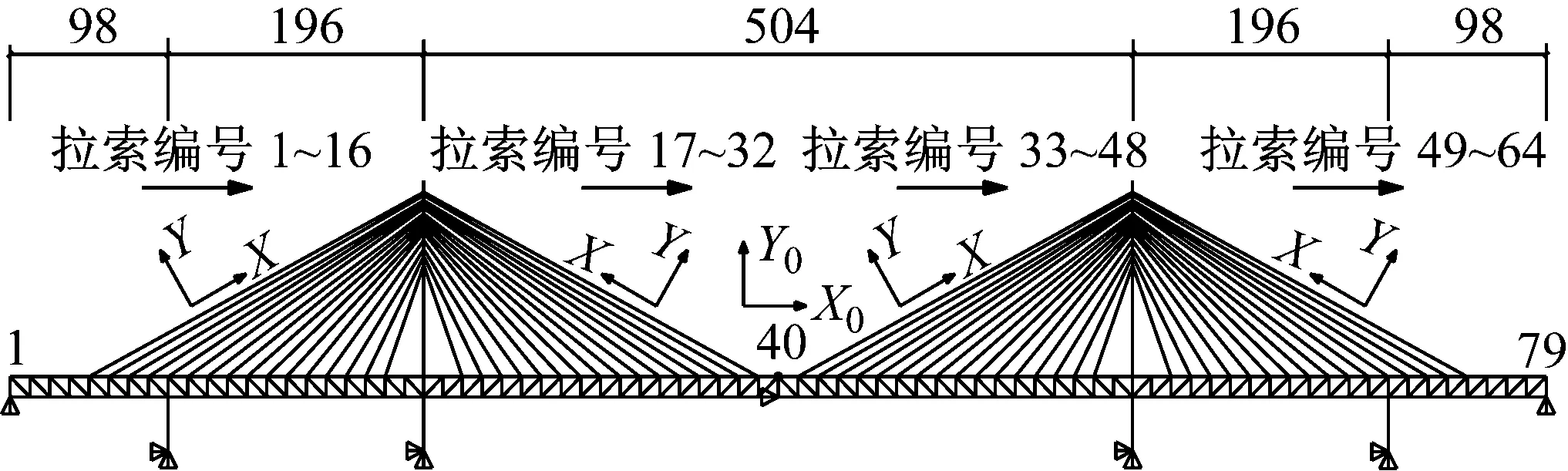
图4 天兴洲大桥平面有限元模型

根据文献[20]以及向桥梁设计单位咨询得到斜拉桥设计参数，由于为有限元模型为2维平面模型，天兴洲大桥斜拉桥3索面中只取其中1索面，桥塔、主梁按照其几何、物理属性的1/3简化(取为原截面积、竖向刚度的1/3)，列车荷载也按照1/3取值。拉索编号从左到右为1～48号拉索。X0Y0为总体坐标系。

主梁、桥塔使用平面梁单元模拟，塔梁连接使用杆单元模拟，拉索使用分段直杆单元模拟。桥塔上靠近中跨、边跨最长的3根拉索分为40段，其他拉索分为20段， 全桥共1 202个节点，1 421个单元。桥塔与辅助墩底部约束全部自由度，主梁两端底部节点约束Y0方向，为了计算需要，跨中底部节点约束X0方向。重力加速度取G=9.8 m/s2。模型阻尼比设为0.05%，阻尼矩阵取全桥前2阶振型计算。

为了考察全桥整体结构的振动特性，首先建立全桥有限元模型(拉索不分段)。先考虑几何非线性计算结构在自重下的静力状态，再计算自振特性，计算结果如图5所示。

图5 全桥前8阶模态(拉索不分段)

Fig.5 The first 8 modes of global bridge (The cables were not divided)

从图5可以看出,全桥结构2维低阶模态以主梁的振型为主。由于拉索不分段，所以图中的模态反映了全桥整体结构的振动特性。

模型计算结果中，天兴洲大桥有限元模型(拉索不分段)X0Y0平面内1、2阶模态(主梁对称竖弯、主梁反对称竖弯)频率分别为0.378 Hz,0.590 Hz。

在文献[20]中使用天兴洲大桥3维空间有限元全桥模型(拉索不分段)计算得到桥梁在X0Y0平面内1,2阶模态(主梁对称竖弯、主梁反对称竖弯)频率分别为0.370 3 Hz, 0.597 7 Hz，与本文结果较为接近，这说明本文的近似处理接近天兴洲大桥的实际情况，本文2维模型的模态计算结果是较为可靠的。

使用拉索分段的天兴洲大桥全桥模型，先考虑几何非线性计算结构在自重下的静力状态，再计算在自振特性，得到模态计算结果如图6所示。

图6 全桥前8阶模态(拉索分段，静力变形有放大)

Fig.6 The first 8 modes of global bridge(The cables were divided and the static shape was amplificatory)

由图6可以看出，当拉索使用分段模型时，拉索的局部振动模态与整体结构的振动模态是混合在一起的。图6中全桥第1阶模态的振型接近图5中全桥第1阶模态的振动而两者频率有所差别，这是由于图6中的模态包含了拉索的局部模态造成的。

由于使用拉索分段模型计算动力特性时全桥拉索局部振动与整体结构振动难以区分，所以，为了对比拉索的局部自振频率与全桥整体结构自振频率，本文使用图5中拉索不分段有限元模型来得到全桥整体自振频率， 使用理论公式单独计算拉索的自振频率。有垂度拉索的自振频率计算公式为

(n=1,2,…)

(10)

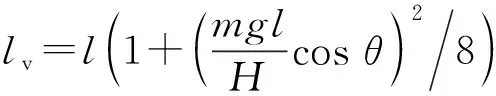
式中：l为拉索两端距离，H为索力；m为拉索每延米质量；E为弹性模量；A为拉索截面积；θ为拉索倾角；g为重力加速度。

根据计算可以得到拉索在自重作用下的成桥索力，使用式(15)得到所有拉索的前n(n=1,2,3…)阶自振频率。全桥为对称结构，全桥整体前10阶自振频率(拉索不分段模型计算)与1～32号拉索的前2阶自振频率对比如图7所示。

图7中J1～J10的横线表示全桥第1～10阶自振频率值。由图中可以看出，斜拉桥较长拉索的自振频率较为接近全桥的低阶频率。

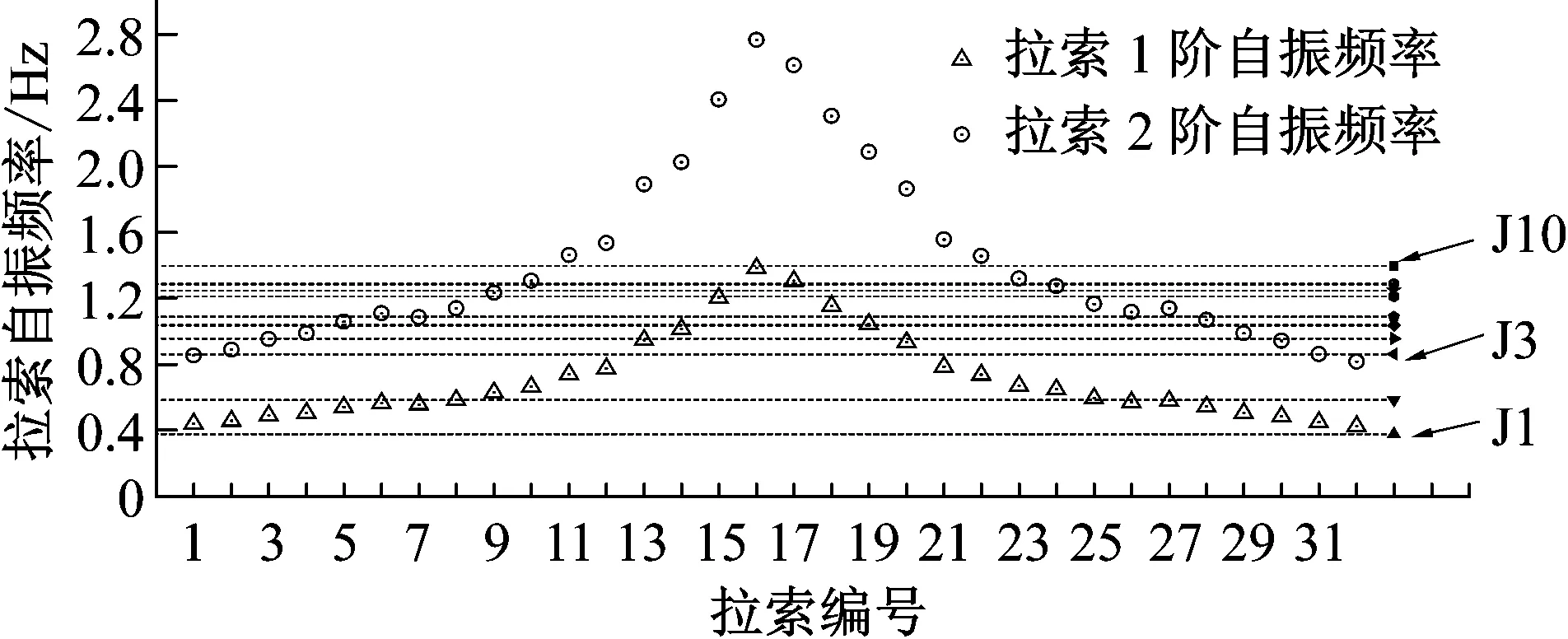
图7 各个拉索前2阶自振频率与全桥前10阶自振频率对比

Fig.7 Comparison between the first 2 orders natural frequency of the cables and the first 10 orders natural frequency of global bridge

仅根据自振频率的对比还不足以判断斜拉桥是否容易在列车动力荷载作用索-梁相关振动作用下发生大幅振动。斜拉桥整体结构导致的索-梁相关振动具体性质还需进一步分析。

2.2 桥梁结构大幅振动导致的索-梁相关振动特性

为了确定拉索发生大幅索-梁相关振动的共振条件，这里首先考察斜拉桥全桥发生大幅共振时拉索的非线性振动特性。本文有限元方法可以考虑结构在静力作用的初始位移，在后文的结果中扣除初始位移仅提取动力作用下的动位移结果。

如图4所示，X0Y0为总体坐标系，为了得到拉索的局部振动计算结果，以每根拉索中连接拉索两端的直线方向(主梁端指向桥塔端)为X轴方向，Y轴方向指向拉索上方(与X轴垂直)，建立各个拉索的局部坐标系，在后面的计算结果分析中，按需求分别提取拉索的1/2点、1/4点(靠近主梁端)沿拉索局部坐标系Y方向的振动计算结果来观察拉索的1阶、2阶大幅振动状态。

如图8所示，在斜拉桥全桥模型中跨1/2点处施加简谐激励P=P0sin(ωt)其中P0=-3.0×105N激励频率为0.369 Hz，与图6中全桥拉索分段模型1阶自振频率值相同。首先，考虑几何非线性计算斜拉桥在自重作用下的静力状态，然后，计算非线性动力时程，共计算8 000步，时间步长0.06 s。

图8 斜拉桥上的动态力

分别计算得到斜拉桥主梁跨中1/2点在总体坐标系Y0方向的振动时程图、频谱图如图9所示。

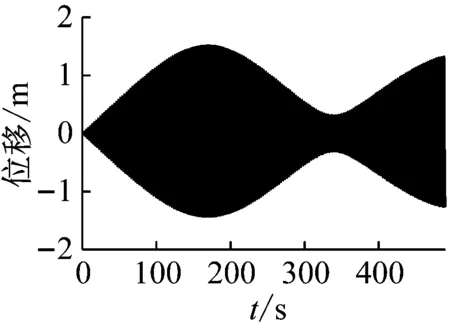
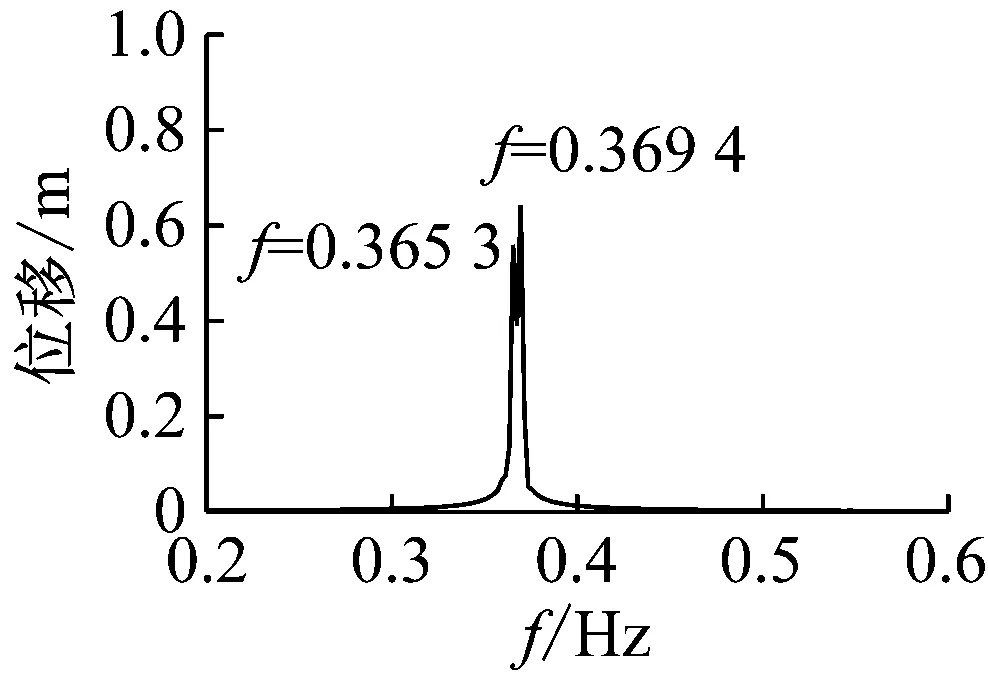
(a) 主梁中跨1/2点振动时程图、频谱图(非线性)

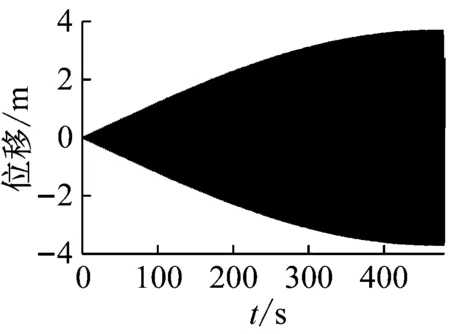
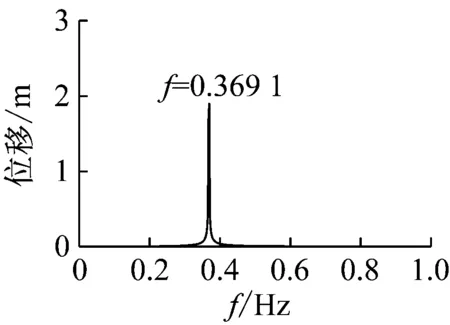
(b) 主梁中跨1/2点振动时程图、频谱图(线性)

图9(a)为使用非线性Newmark-β法动力时程计算得到的结果。可以看出，外激励接近全桥1阶频率，全桥结构发生1阶振型的共振，中跨1/2节点振幅随时间迅速增大，但由于全桥结构的振动几何非线性作用，结构响应频率与振幅有关，振幅不会一直增加，而是呈现 “拍振”的非线性振动性质。跨中节点40振幅达到约1.5 m以上时，发生了拍振现象，共振振幅开始周期性涨落。

图9(b)为使用线性Newmark-β法动力时程计算结果，与图9(a)计算结果不同，线性动力时程计算中由于结构刚度矩阵不变，当外激励与全桥自振频率接近的时候，全桥结构会发生共振，根据振动理论，共振振幅会持续增加直至结构阻尼确定的上限。

对比图9(a)与9(b)可以发现，当全桥结构振动达到约1.5 m的时候结构才会进入较为明显的非线性振动状态。所以，对于斜拉桥，如果发生较大幅度振动，应当使用非线性动力时程积分算法。

使用图8加载模型，非线性动力时程计算得到斜拉桥各个拉索的1/2点在局部坐标系Y方向最大振幅如图10所示。

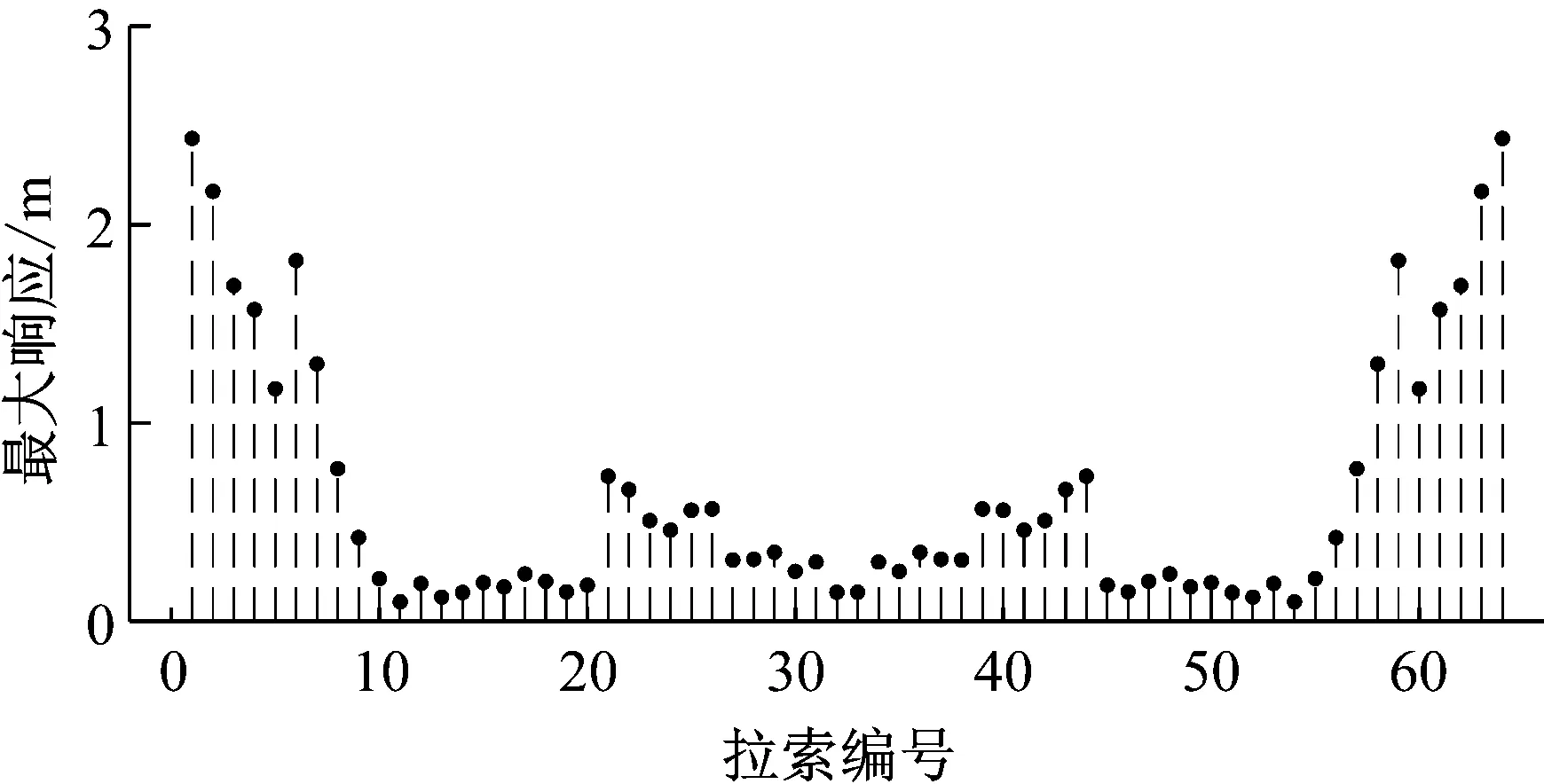
图10 斜拉桥各个拉索1/2点最大振幅

由于全桥为对称结构，激励在跨中1/2点，所以图10左右对称。由图10可以看出，由于全桥在外激励作用下发生了1阶共振，边跨最长拉索在索-梁相关振动的作用下发生较大幅度的振动，其他较长拉索也发生了较大幅度振动。

得到拉索1的1/2点在拉索局部坐标系Y方向的振动时程图、频谱图如图11所示。

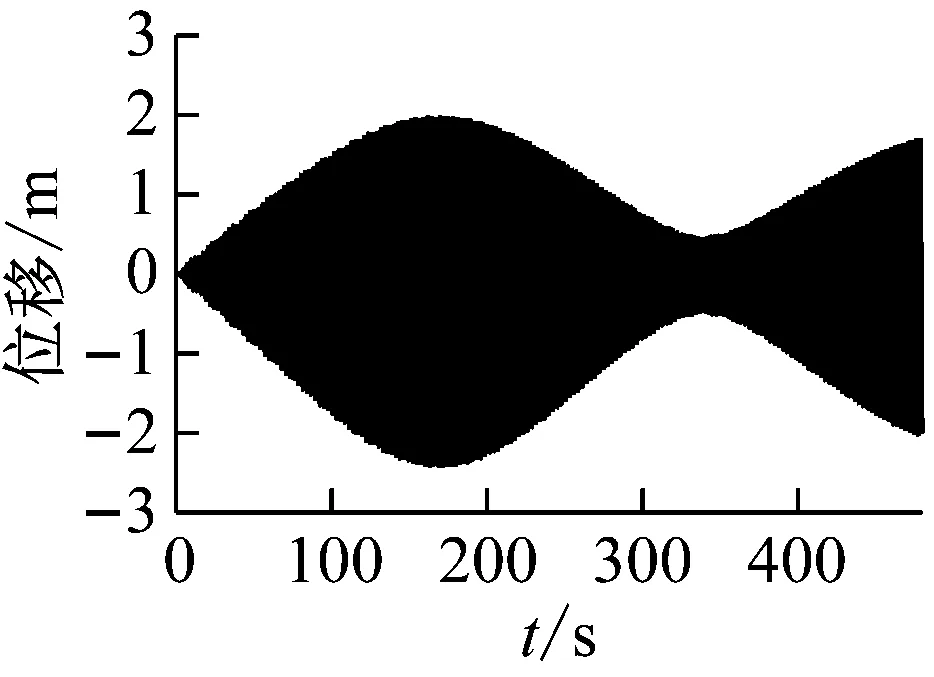
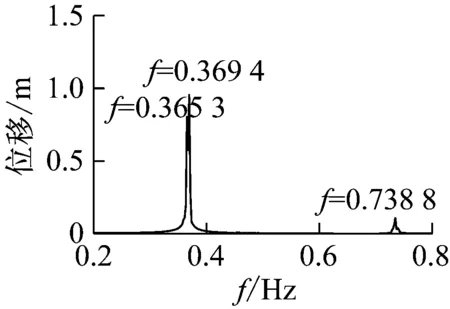
图11 拉索1的1/2点振动时程图、频谱图

由于拉索1的1阶自振频率(0.425 Hz)较为接近全桥自振频率(0.369 Hz)，且由理论与已有研究结论可知，对于频率较低的长索，索-梁相关振导致的强迫激励下非线性振动响应区间通常较宽，可以判断拉索在索-梁相关振动的作用下发生了强迫激励下的1∶1主共振。

激励在斜拉桥跨中，但边跨较长拉索发生了较为明显振动，这说明，不同于简化索-梁组合结构，在实际斜拉桥全桥尺度下，外激励注入的能量通过主梁、桥塔进行了传递，导致自振频率达到共振条件的拉索都发生了大幅振动。

如图12所示，为了激发全桥发生2阶共振(全桥2阶)，根据图6的全桥模态，在斜拉桥主梁跨中1/4点施加简谐力P=P0sin(ωt)其中P0=-3.0×105N，励频率为0.590 Hz(与图5中全桥2阶频率值相同)，计算步设置与图8中相同。

图12 斜拉桥主梁跨中1/4点上的简谐力

得到斜拉桥跨中主梁1/4点(节点31)在总体坐标系Y0方向的振动时程图、频谱图如图13所示。

从图13中时程图可以看出，主梁1/4点在外激励作用下发生了较大幅度振动，最大振幅接近0.4 m，跨中主梁1/4点振动频率接近全桥的2阶自振频率，简谐激励激发了全桥发生2阶大幅非线性共振。

各个拉索的1/2点沿拉索局部坐标系Y方向最大振幅如图14所示。

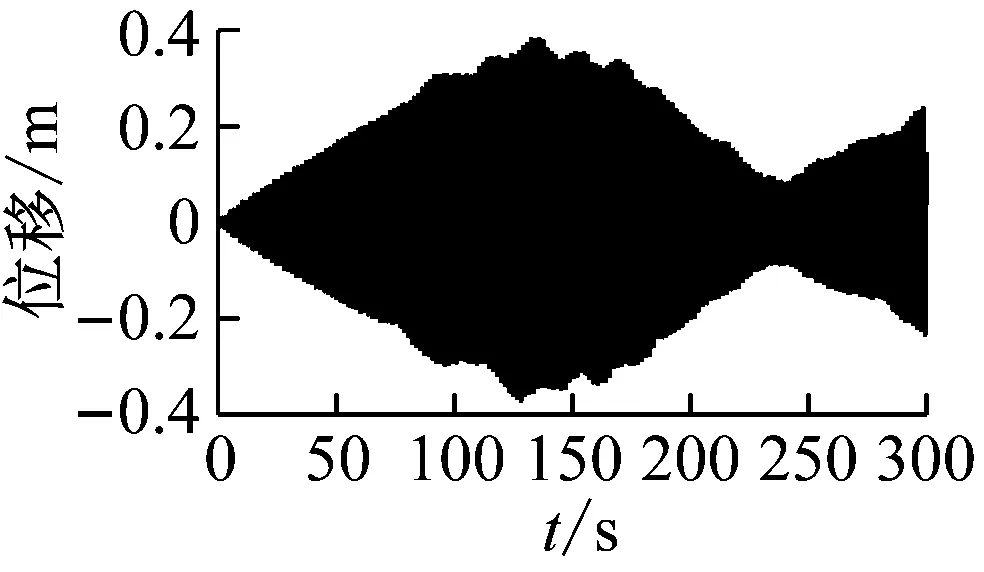
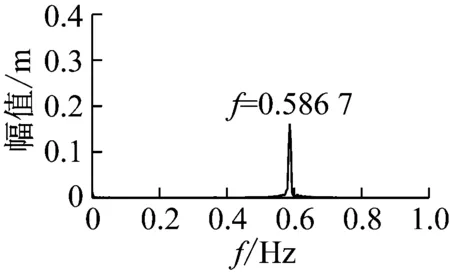
图13 跨中主梁1/4点振动时程图、频谱图

图14 斜拉桥各个拉索1/2点最大振幅

从图14中可以看出，编号为8,25,40,57号拉索发生了大幅振动，最大振幅达到了约3 m，这些拉索的1阶自振频率依次分别为0.575 Hz, 0.583 Hz, 0.583 Hz, 0.575 Hz，其中8与25号这一组拉索沿左桥塔对称布置，40与57号这一组拉索沿右桥塔对称布置，这两组拉索沿全桥对称布置。它们的1阶自振频率都接近于全桥的2阶振动频率，都在索-梁相关振动的作用下发生大幅度振动，且它们附近的拉索由于自振频率接近都发生了较大幅度的振动。

提取拉索8的1/2点在拉索局部坐标系Y方向的振动时程图、频谱图如图15所示。

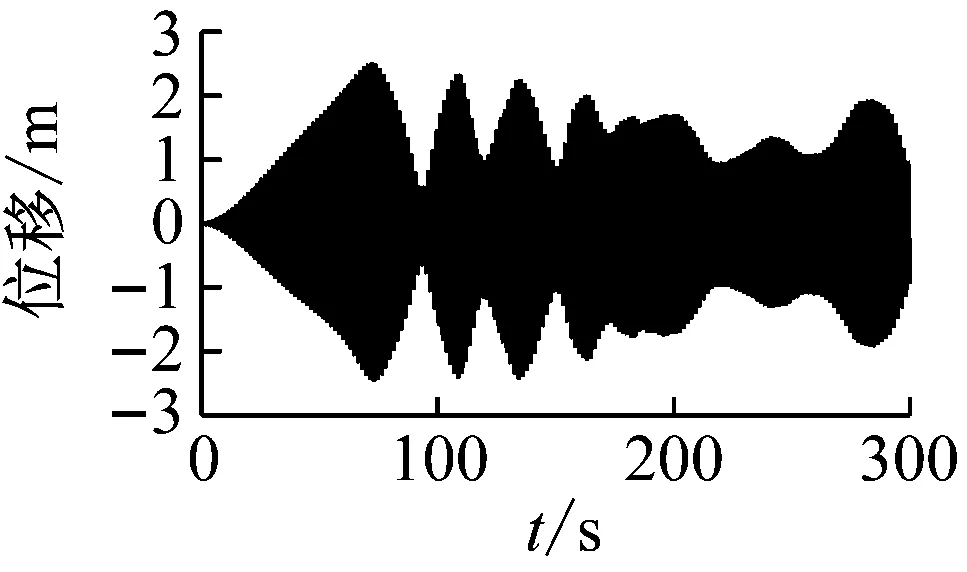
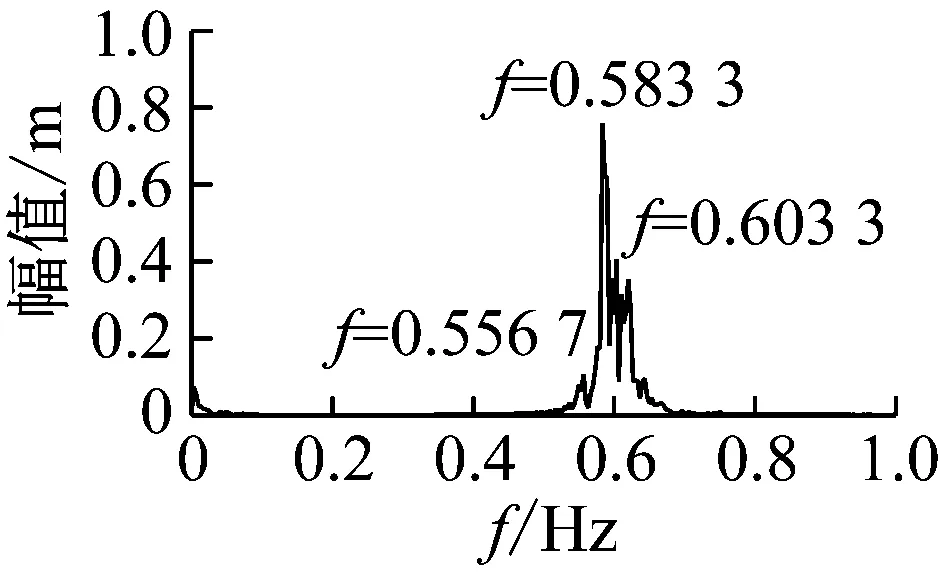
图15 拉索8与拉索25的1/2点振动时程图、频谱图

观察图15中的时程图，可以发现拉索1/2点发生了大幅振动，而频谱图则说明拉索的大幅振动为1阶振动，所以，根据理论原理判断，较大振幅的拉索都发生了1阶的1∶1主共振。

以上计算结果表明，当天兴洲大桥全桥发生2阶共振时，全桥的2阶共振频率接近全桥中某些拉索的共振区(对比图7)，外激励注入能量同样通过主梁、桥塔传递，导致沿全桥与之频率接近的拉索发生大幅度的非线性1∶1主共振。由于主梁的位移响应较大，所以拉索的共振振幅较大。

2.3 最长拉索的1∶1主共振

在天兴洲大桥上，跨中拉索(第32号拉索)最长且中跨无辅助墩，所以本文认为中跨拉索更容易在索-梁相关振动作用下发生振动。

已知跨中最长拉索(32号拉索)的1阶自振频率为0.430 Hz。如图16所示，在32号拉索主梁端节点上(节点39)施加简谐激励P=P0sin(ωt)其中P0=-3.0×105N激励频率为0.43 Hz(与拉索32的1阶自振频率值相同)，动力时程计算时间步长取0.05 s，计算6 000步。

图16 拉索32端点上的简谐力

由于外激励简谐力频率接近拉索的1阶自振频率，所以根据非线性振动理论，拉索会在索-梁相关振动的作用下发生1∶1主共振。

计算得各个拉索的1/2点在拉索局部坐标系Y方向最大振幅如图17所示。

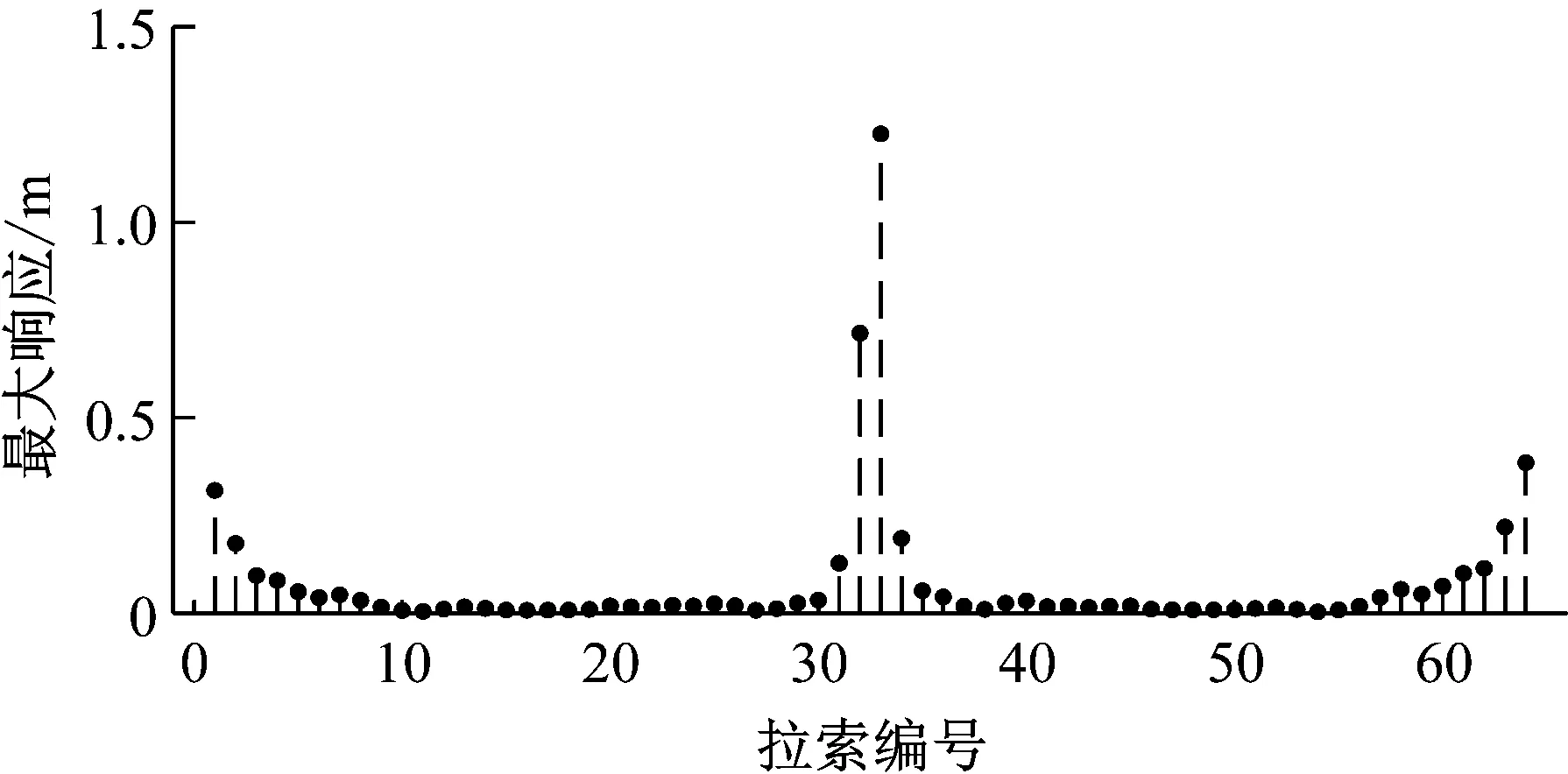
图17 斜拉桥各个拉索的1/2点振动最大振幅

从图17中可以看出，由于外激励接近跨中以及边跨拉索的1阶自振频率，最长的几根拉索在端点位移激励作用下发生了大幅振动。

得到拉索32在拉索局部坐标系Y方向、斜拉桥主梁跨中1/2点沿总体坐标系Y0的振动时程图、频谱图如图18所示。

观察图18，从时程图可以看出，拉索发生了大幅振动，从频谱图可以判断拉索发生了1阶的1∶1主共振。由于斜拉桥整体结构的能量传递效应，拉索32及其附近与之自振频率接近的拉索都发生了索-梁相关振动导致的较大幅度的1阶主共振。

由于外激励位于主梁跨中，主梁位移响应相对较明显，达到约0.05 m。外激励与斜拉桥全桥自振频率有一定的差别，所以跨中振动幅度较小端点位移激励幅值较小。

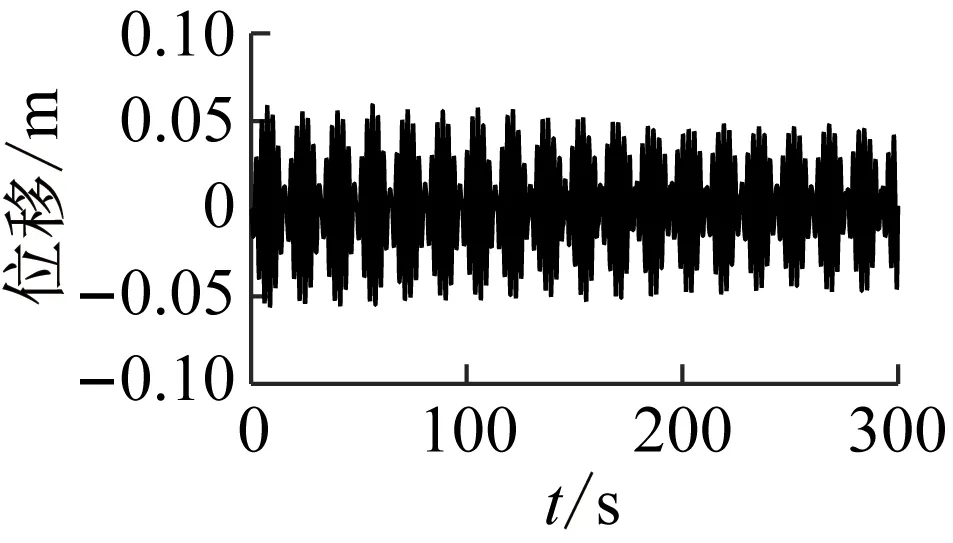
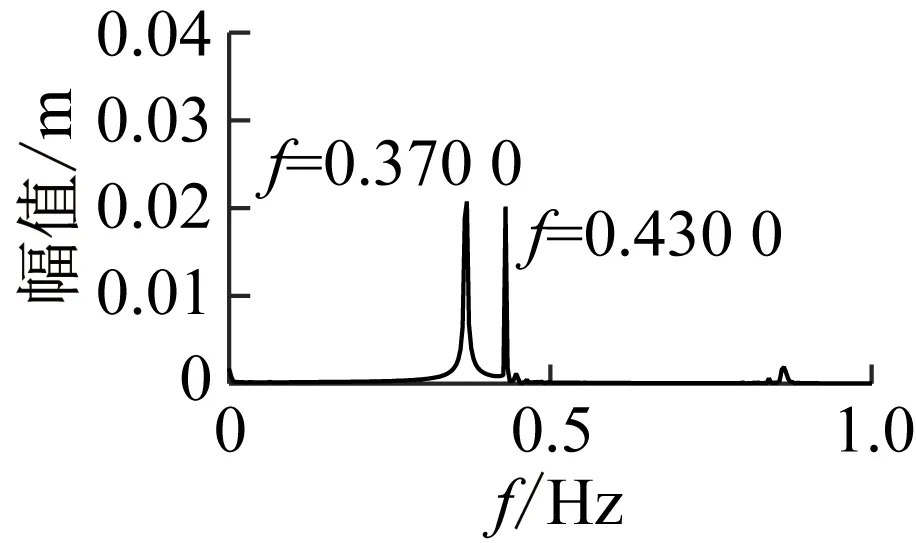
(a) 主梁1/2点振动时程图、频谱图

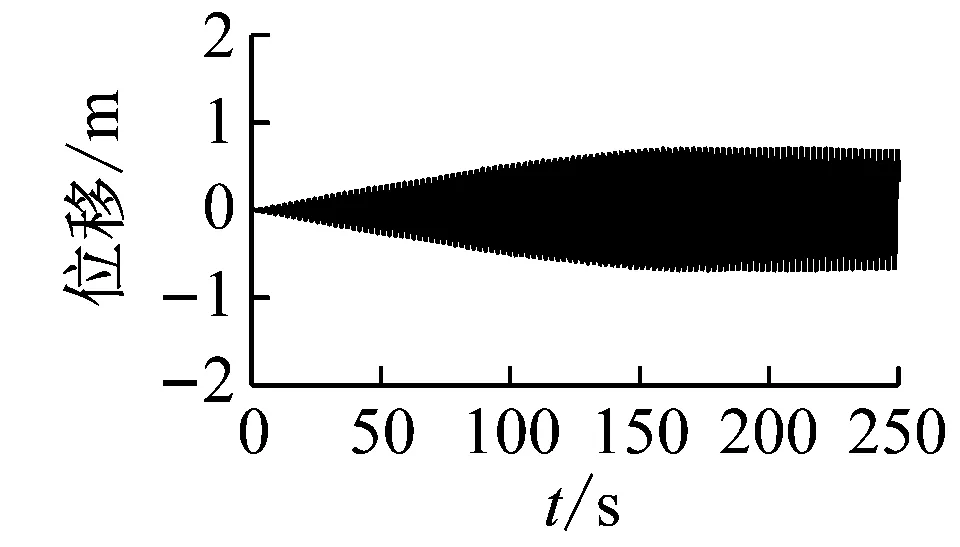
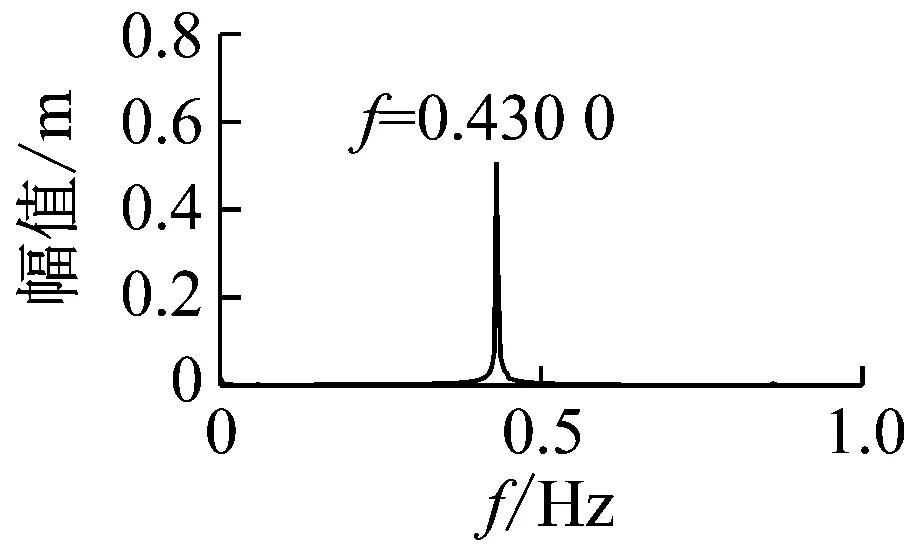
(b) 拉索32的1/2点振动

Fig.18 The time-history curve and spectrogram of the 1/2 point cables and 1/2 point of middle span

2.4 最长拉索的2∶1参数共振

为了考察斜拉桥中跨的最长拉索可能发生的参数振动情况。与图16中施加简谐力相同，简谐力频率设置为0.43×2=0.86 Hz(为拉索32的1阶自振频率值的2倍)。

由于外激励频率接近拉索1阶频率的2倍，拉索上可能发生1阶参数共振同时发生的2阶主共振。计算得各个拉索的1/2点与1/4点在拉索局部坐标系Y方向最大振幅如图19所示。

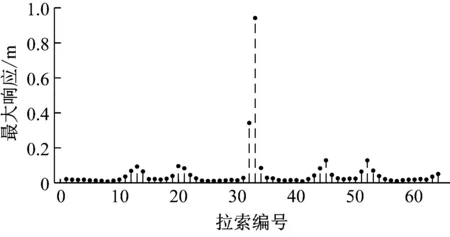
(a) 各个拉索的1/2点振动最大振幅

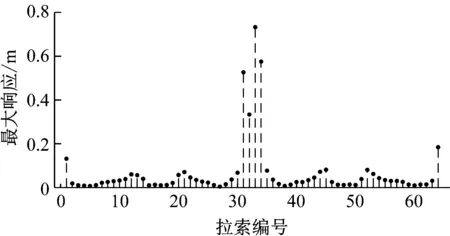
(b) 各个拉索1/4点振动最大振幅

Fig.19 The largest amplitude of the 1/2 point and 1/4 point of the cables in the cable-stayed bridge under external excitation

根据图19(a)，可以看出，在简谐外激励作用下，拉索32,33的1/2点发生了较大幅度的振动，得到它们在拉索局部坐标系Y方向的振动时程图、频谱图如图20所示。

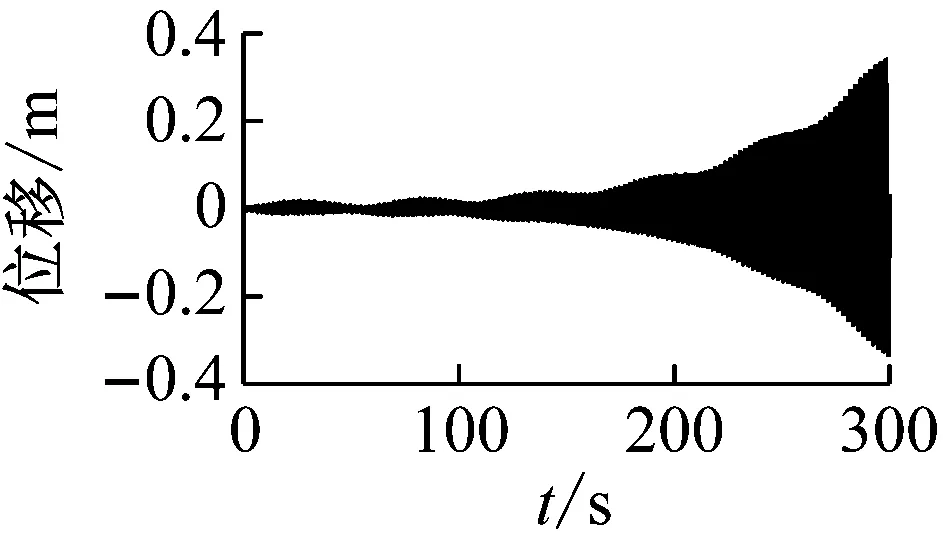
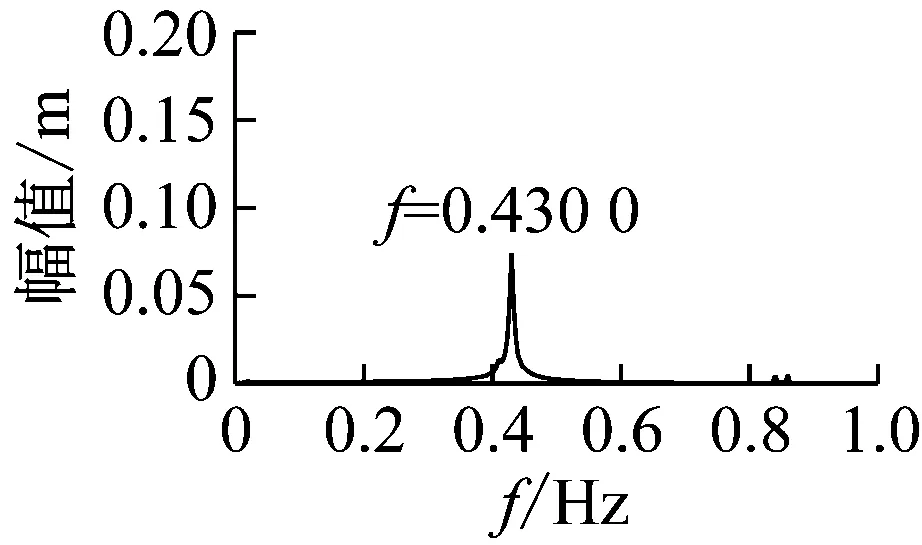
图20 拉索与主梁1/2点振动时程图、频谱图

根据图20，从时程图可以看出，拉索1/2点发生了大幅振动，从频谱图可以看出，拉索的大幅振动为1阶振动。所以，可以判断拉索在端点位移激励下发生了1阶的2∶1参数共振。

得到拉索32的1/4点在拉索局部坐标系Y方向的振动时程图、频谱图如图21所示。

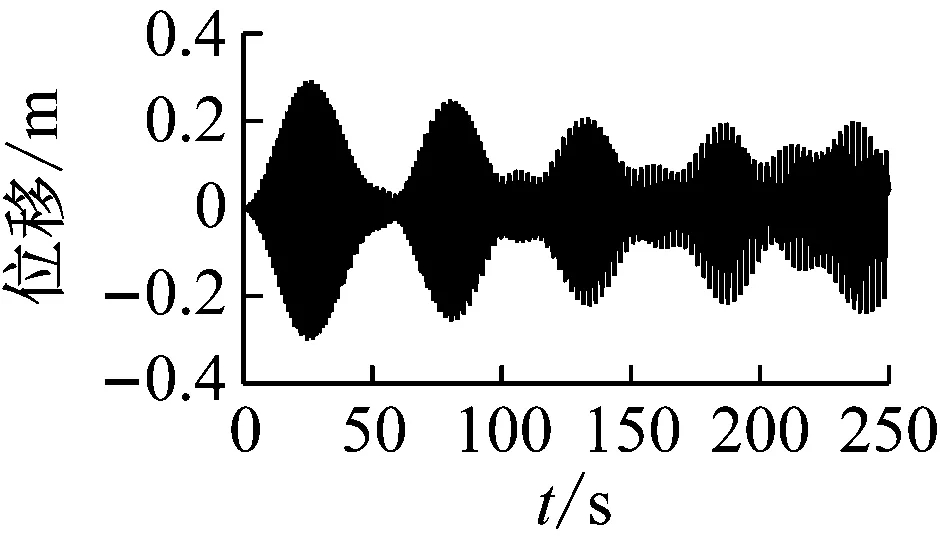
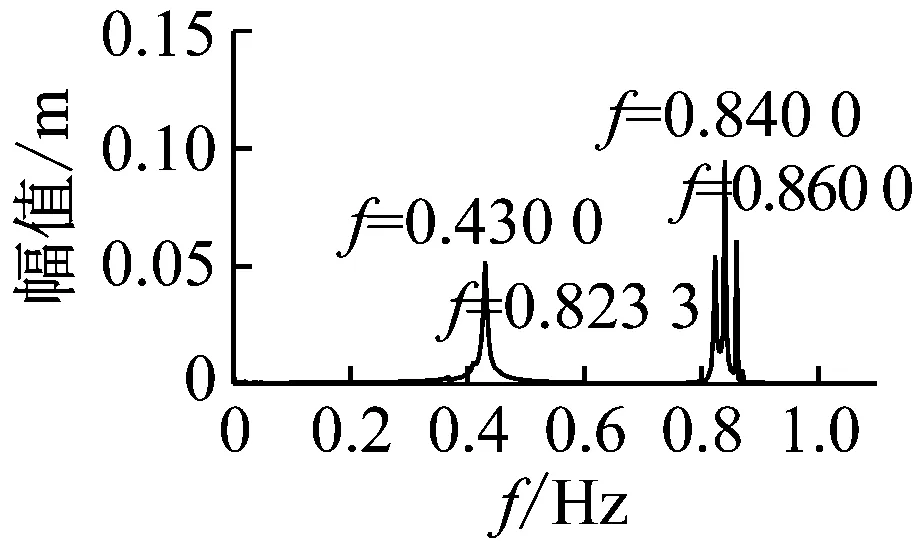
图21 拉索32的1/4点的振动时程图、频谱图

根据图21，可以看出拉索32的1/4点发生了较大大幅振动，从频谱图可以看出振动的主要较大响应频率约为0.83～0.86 Hz(本文认为，频率成分复杂应当是由于非线性振动效应造成)，接近拉索1阶自振频率的2倍，因此可以判断拉索在频率为0.86 Hz的端部简谐力作用索-梁相关振动导致了拉索发生了较大幅度的2阶的1∶1主共振。

对于拉索32，对照观察图20与图21(拉索1/2点与1/4点大幅振动)，可以发现，拉索上同时发生了1阶的2∶1参数共振与2阶1∶1主共振。但由图20可知，拉索1阶的1∶1参数共振的振幅随激励时间增加较为缓慢(尽管外激励条件较为理想，但拉索在约200 s时1/2点的振动幅度才有较为明显的增加)，而2阶主共振的振幅随简谐激励持续时间迅速增大(拉索1/4点的振幅在约20 s内达到了振幅峰值)。发生1∶1的2阶主共振拉索为31,34，发生2∶1参数共振的拉索仅有拉索32与33。

综上所述，可以判断，对于斜拉桥跨中最长拉索，在端点简谐激励接近拉索1阶自振频率2倍时，拉索上会同时发生1阶的2∶1参数共振与2阶1∶1主共振，但2∶1参数共振相对不容易发生，拉索的大幅振动以2阶1∶1主共振为主，具体表现为：拉索1/4点的振幅随激励时间迅速增大，1/2点振幅随时间增长缓慢。因此，本文认为，在实际大跨度斜拉桥的索-梁相关振动分析中应主要考虑拉索上发生的1∶1主共振(1阶或n阶)，可以不主要考虑2∶1参数共振的作用。

2.5 非跨中拉索的主共振与参数共振

选取斜拉桥中跨1/4点附近，拉索24作为考察对象。如图22所示，在拉索24主梁上端点处(节点31)施加简谐力如图22所示。

图22 斜拉桥上的简谐力

计算已知拉索24的1阶自振频率为0.633 Hz。简谐激励为P=P0sin(ωt)其中P0=-3.0×105N激励频率取为0.633 Hz，动力时程计算时间步长取0.05 s，计算6 000步。得各个拉索的1/2点在拉索局部坐标系Y方向最大振幅如图23所示。

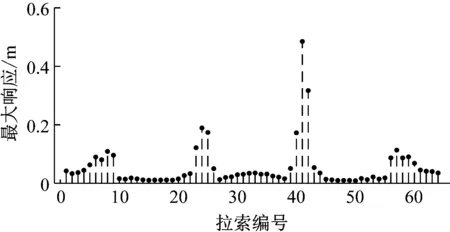
图23 外激励作用下拉索的1/2点

由图23可以看出，拉索24及其沿全桥分布与之频率相近的拉索(拉索9,41,58)都发生了较大幅度的振动。

得到拉索24、41的1/2点在拉索局部坐标系Y方向的振动时程图、频谱图如图24所示。

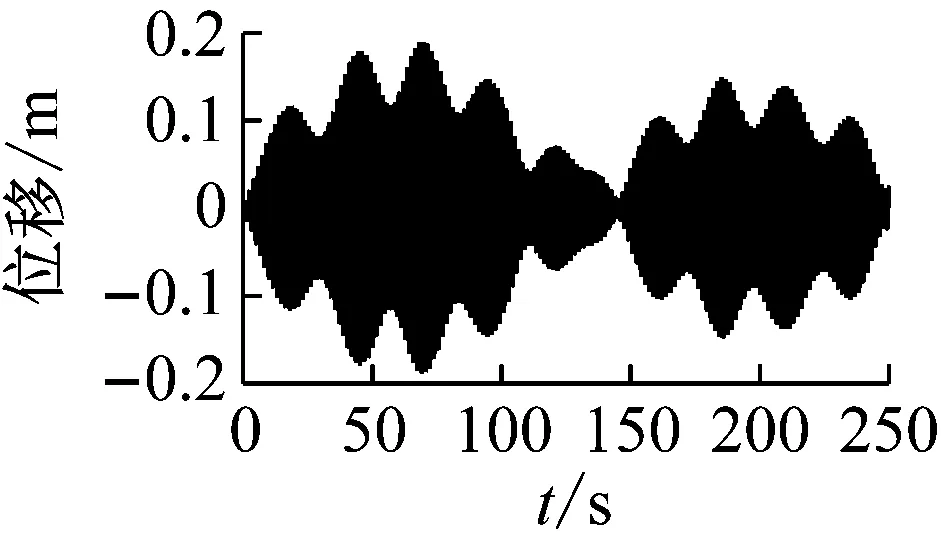
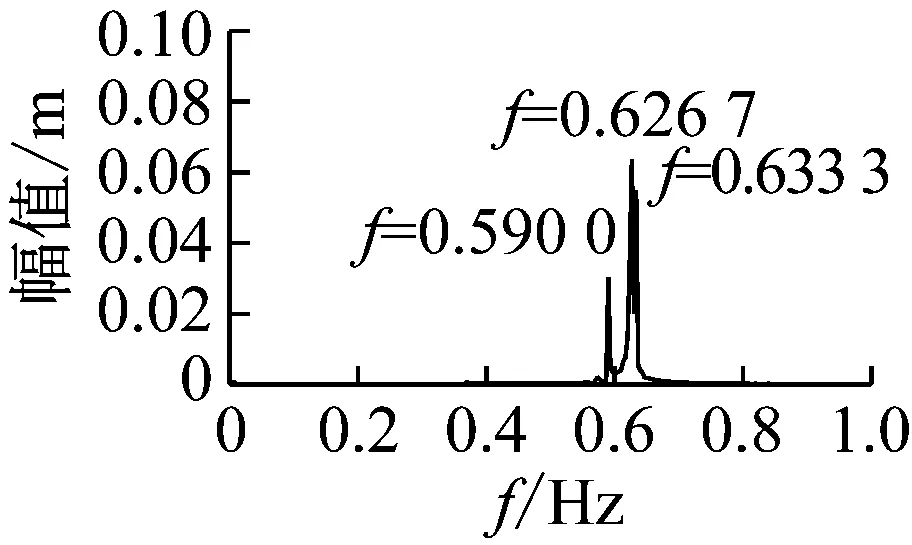
图24 拉索24与41的1/2点振动时程图、频谱图

由图24可以判断，由于简谐激励的频率接近拉索24的1阶自振频率，拉索24及全桥与之频率接近的拉索在主梁、桥塔的能量传递效应下都发生较大幅度的1阶的1∶1主共振。

为了考察拉索24是否可能发生的2∶1参数共振，将图20中的简谐力频率设置为1.266 Hz(拉索24的1阶频率的2倍)，计算得各个拉索的1/2点与1/4点在拉索局部坐标系Y方向最大振幅如图25所示。

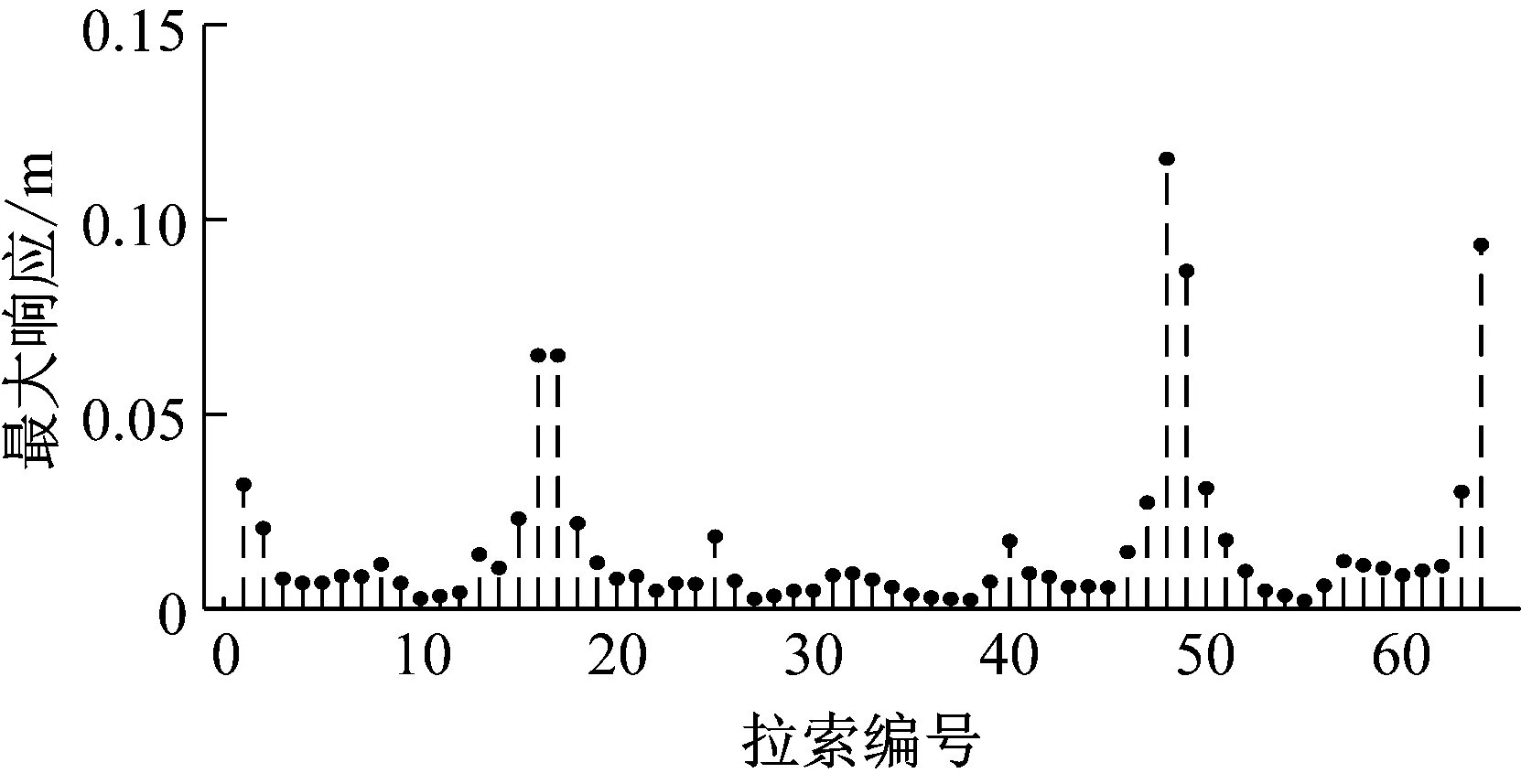
(a) 各个拉索1/2点最大振幅

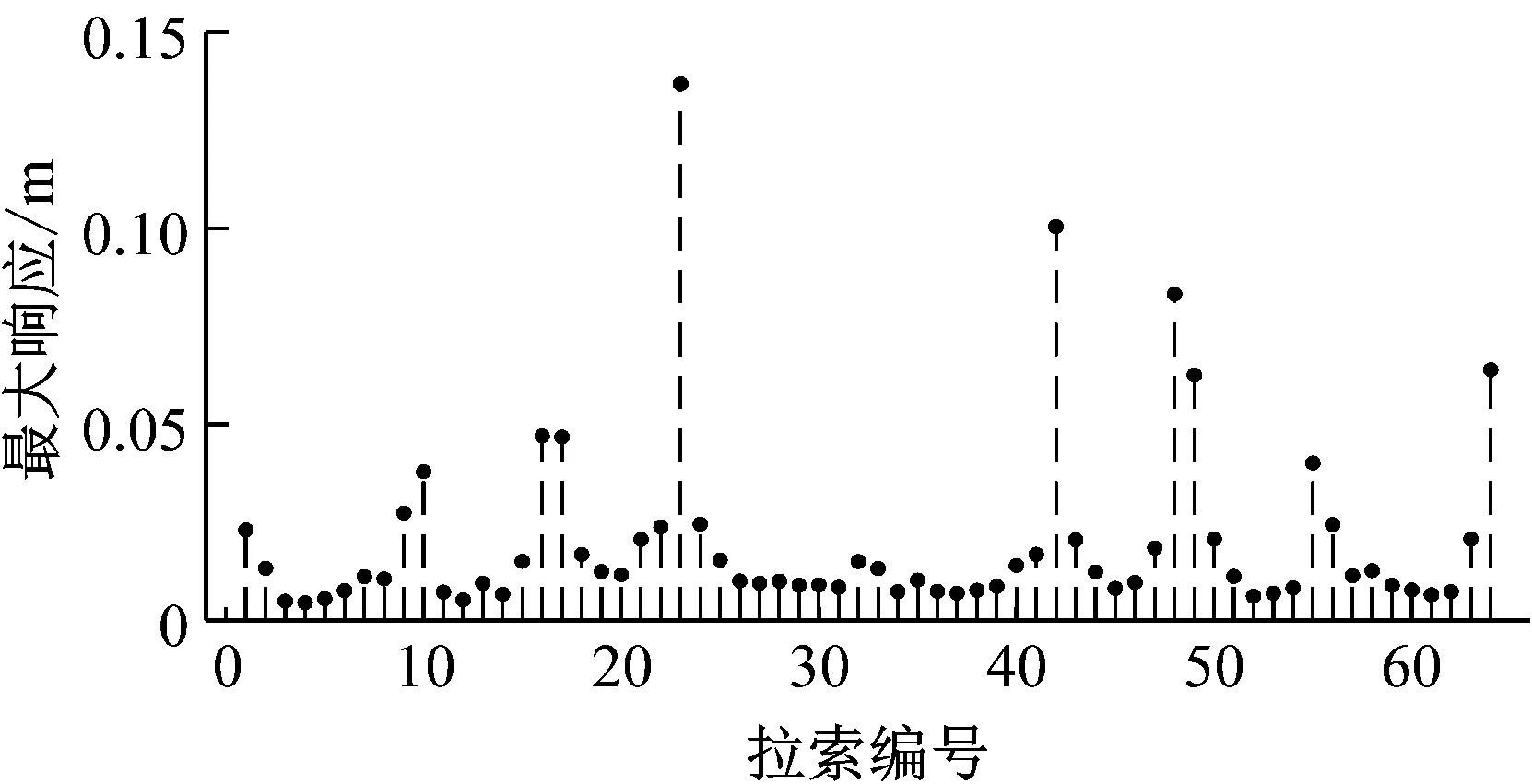
(b) 各个拉索的1/4点最大振幅

Fig.25 The largest amplitude of the 1/2 point and 1/4 point of the cables in the cable-stayed bridge under external excitation

从图25中可以看出，在外激励作用下各个拉索的1/2点与1/4点均未发生较大幅度的振动。这说明，由于远离跨中时，结构刚度更大，结构的非线性效应更为明显，较高频率简谐外激励造成的主梁振动更小，阻尼对拉索大幅高频率振动的抑制作用更为明显，索-梁相关振动不容易导致拉索发生2∶1参数共振或1∶1主共振。

3 列车-桥梁耦合动力作用下斜拉桥索-梁相关振动特性

在第3节中，我们通过施加理论上的理想外部激励讨论了铁路斜拉桥索-梁相关振动达到大幅振动(1∶1主共振，2∶1参数共振)的共振条件。可以认为，对于大跨度铁路斜拉桥，在实际运营过程中，如果列车作用能达到或接近上述共振条件则会导致拉索发生较大幅度索-梁相关振动。所以，这里使用拉索分段的全桥模型，通过车桥耦合振动计算来考察桥梁是否会发生拉索大幅振动的情况。

首先计算1列列车以90 km/h通过桥梁时，各个拉索1/2点的最大响应如图26所示。

图26中可以看出，由于全桥对称，所以拉索的最大响应也是基本对称的，最长的拉索1和拉索32响应最大。这里，提取跨中主梁1/2点、拉索1和拉索32的1/2点的列车过桥动力时程计算结果如图27所示。

从图26与图27都可以看出，列车以90 km/h速度通过桥梁没有导致拉索大幅响应。图27中可以看出，列车通过桥梁的等效外激励频率也较低，本文认为，列车作用更接近一个静力过程。

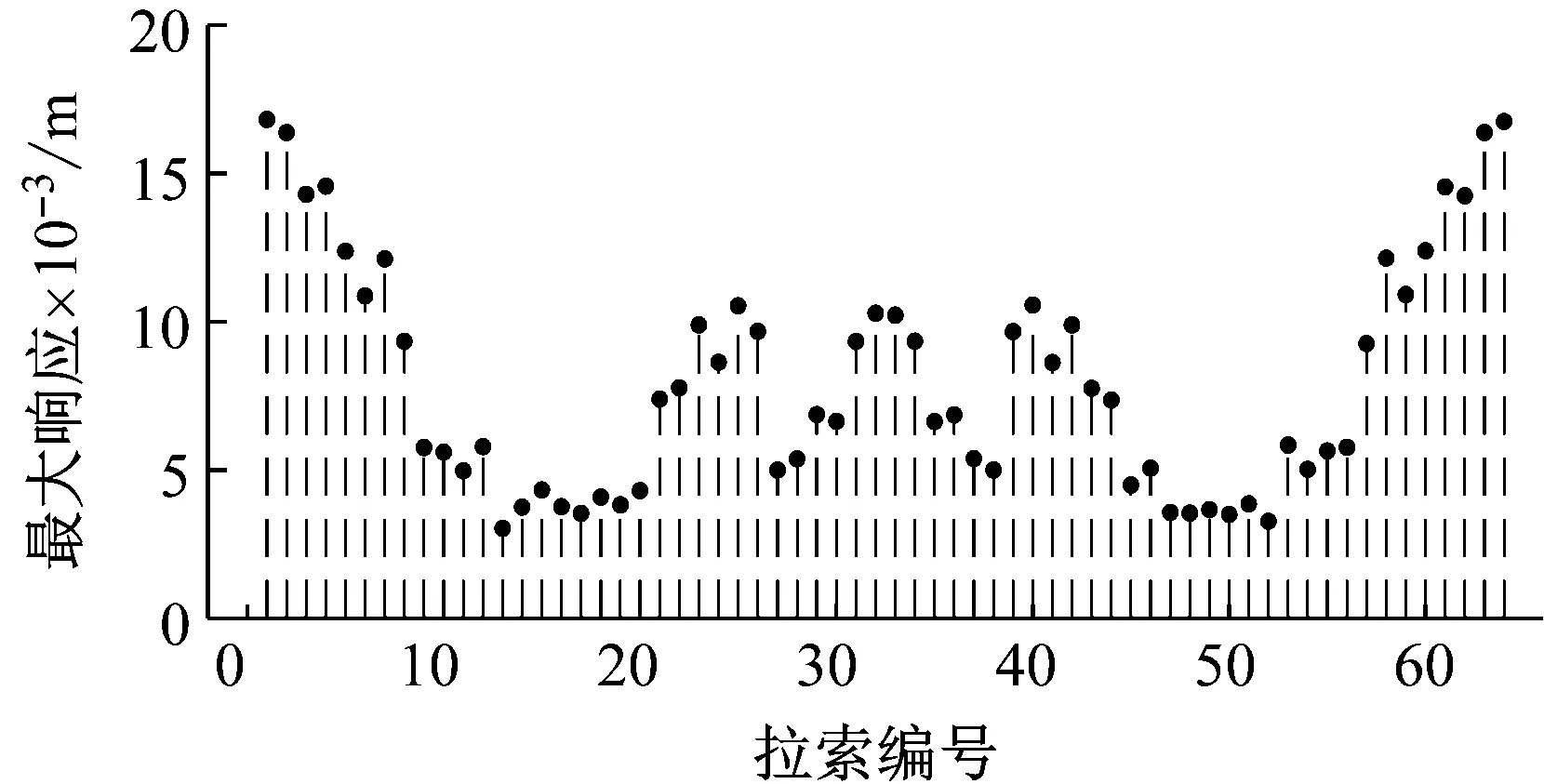
图26 列车作用下桥梁各个拉索1/2点最大响应(v=90 km/h)

Fig.26 The largest amplitude of the 1/2 point and 1/4 point of the cables in the cable-stayed bridge by a train(v=90 km/h)

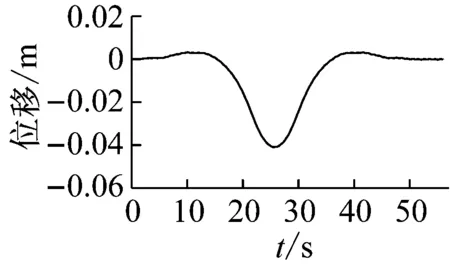
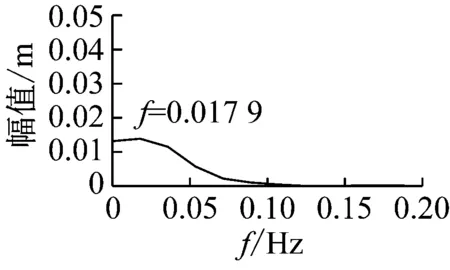
(a) 跨中1/2点节点振动时程图、频谱图

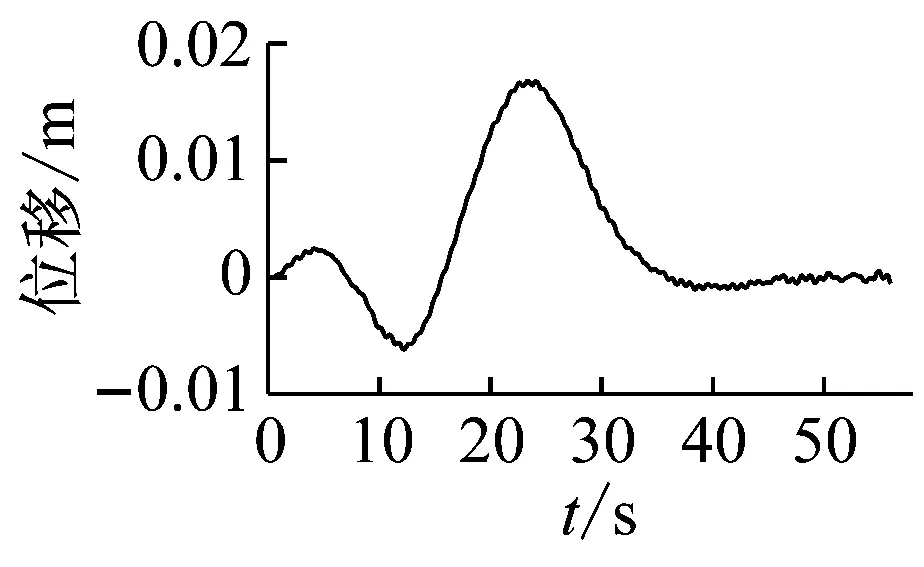
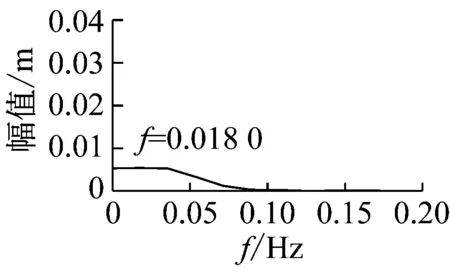
(b) 拉索1 的1/2点的振动时程图、频谱图

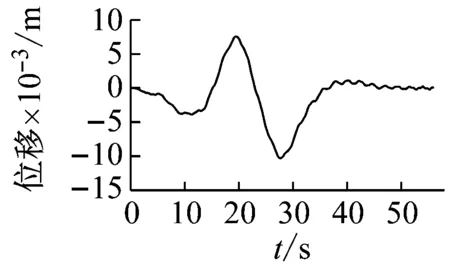
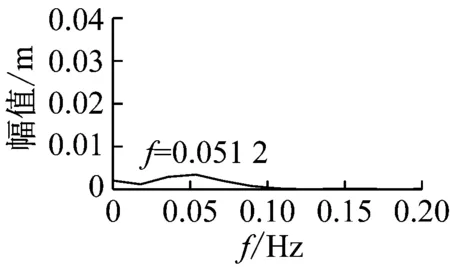
(c) 拉索32的1/2点振动时程图、频谱图

Fig.27 The time-history curve and spectrogram of 1/2 point main girder and the 1/2 points of cable No.32 and No.34

得到分别使用线性计算与非线性计算时，对于拉索32，一列列车过桥造成的拉索索力增量变化如图28所示。

图28中可以看出，使用线性与非线性动力时程计算差别很小。这说明对于大跨度铁路斜拉桥，结构较难进入明显的非线性动力状态，如图9计算结果，主梁跨中达到1.5 m振幅时，才得到全桥明显的非线性振动状态，因此，使用线性计算能提升计算速度也能得到满足工程计算要求的结果。

天兴洲大桥最多可以承受4列高速列车通过，为了得到较为极端情况下的结果，这里计算4列列车同时、同向行驶通过天兴洲大桥(列车的车辆荷载按照规范折减)，且将列车的行驶速度设置为200 km/h，得到计算结果如图29所示。

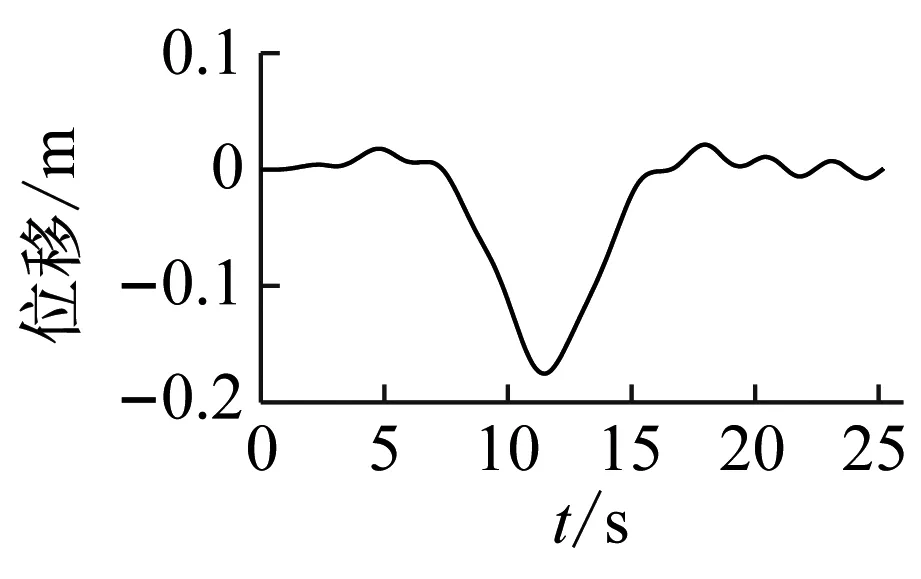
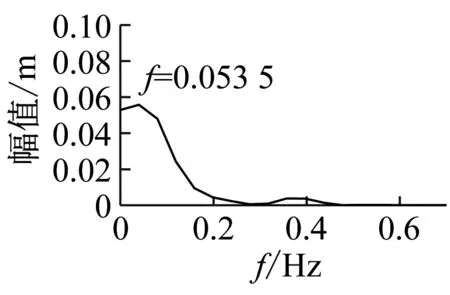
(b) 主梁跨中1/2点振动时程图、频谱图

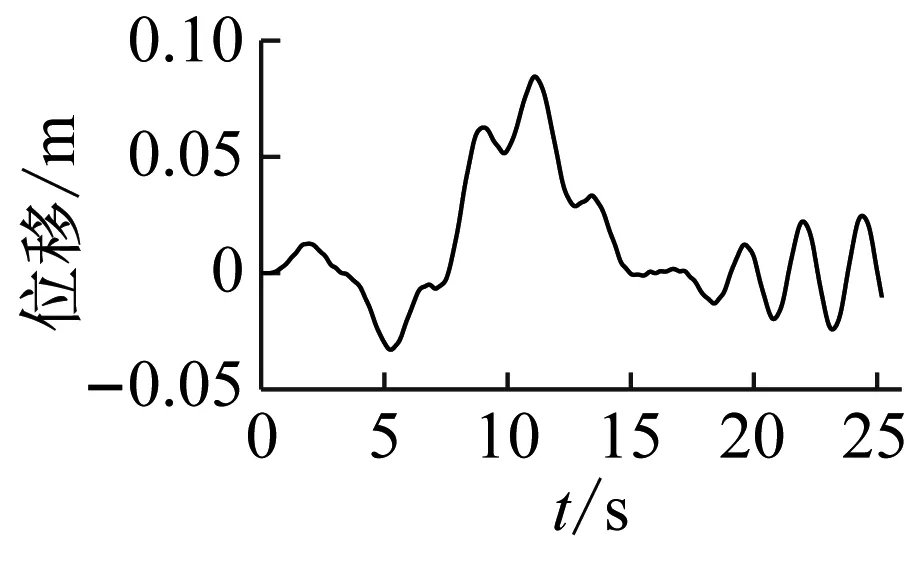
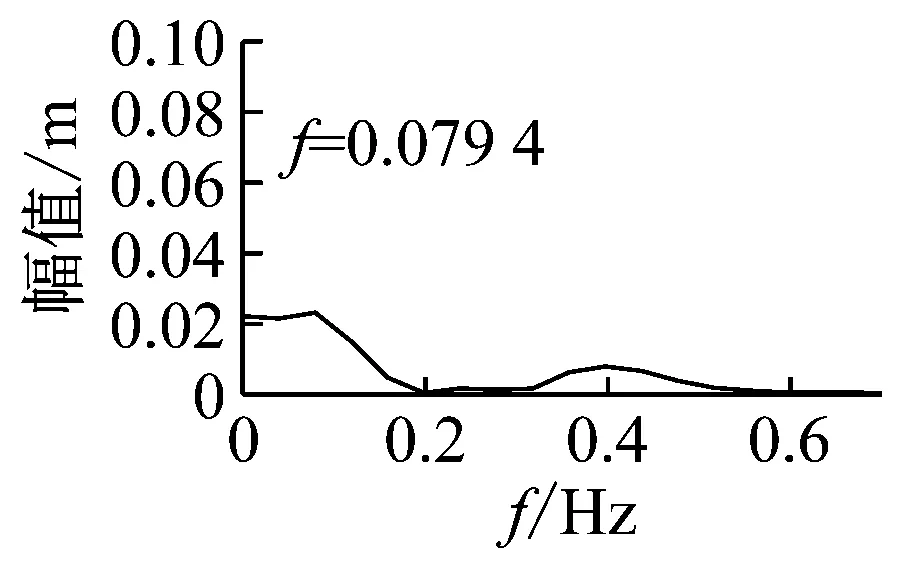
(c) 拉索1振动时程图、频谱图

(d) 拉索32振动时程图、频谱图

Fig.29 Calculation results of vibration of the main girder and cable by four trains on same directions(v=+200 km/h)

由图29可以看出，在较为极端的情况下，4辆列车以200 km/h速度同时通过天兴洲大桥也未造成拉索大幅振动。由于荷载较大，拉索1的最大振幅约为0.08 m，斜拉桥跨中1/2点振动幅度约为0.16 m。

对照图9计算结果，也说明全桥结构在相对较小幅度的振动状态时，斜拉桥的受力状态是接近线性的。列车过桥同样接近一个静力过程，桥梁、拉索的振动频率都较低。考虑实际情况中不会出现4列列车同时以较高速度通过的情况，所以实际列车荷载作用下拉索与桥梁的振动响应幅值、频率也应当是更小的。

计算双车对开工况，正向行驶列车为图4模型中从左到右行驶(v=+120 km/h)，逆向行驶车辆为从右到左(v=-90 km/h)，计算结果如图30所示。

从图30中可以看出，双车对开导致的拉索最大响应也较小，最大约0.04 m。32号拉索的振动时程图与单车过桥相比只是形状与最大幅值有一定的变化，但无大幅振动发生。

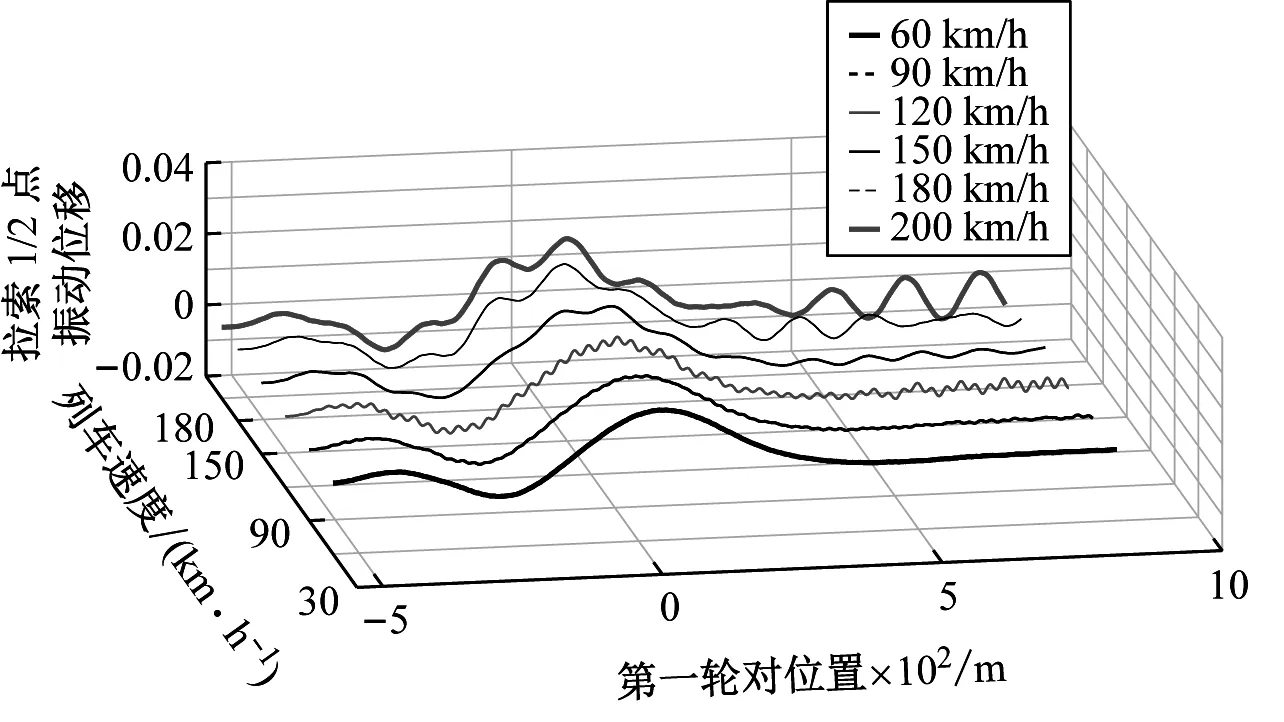
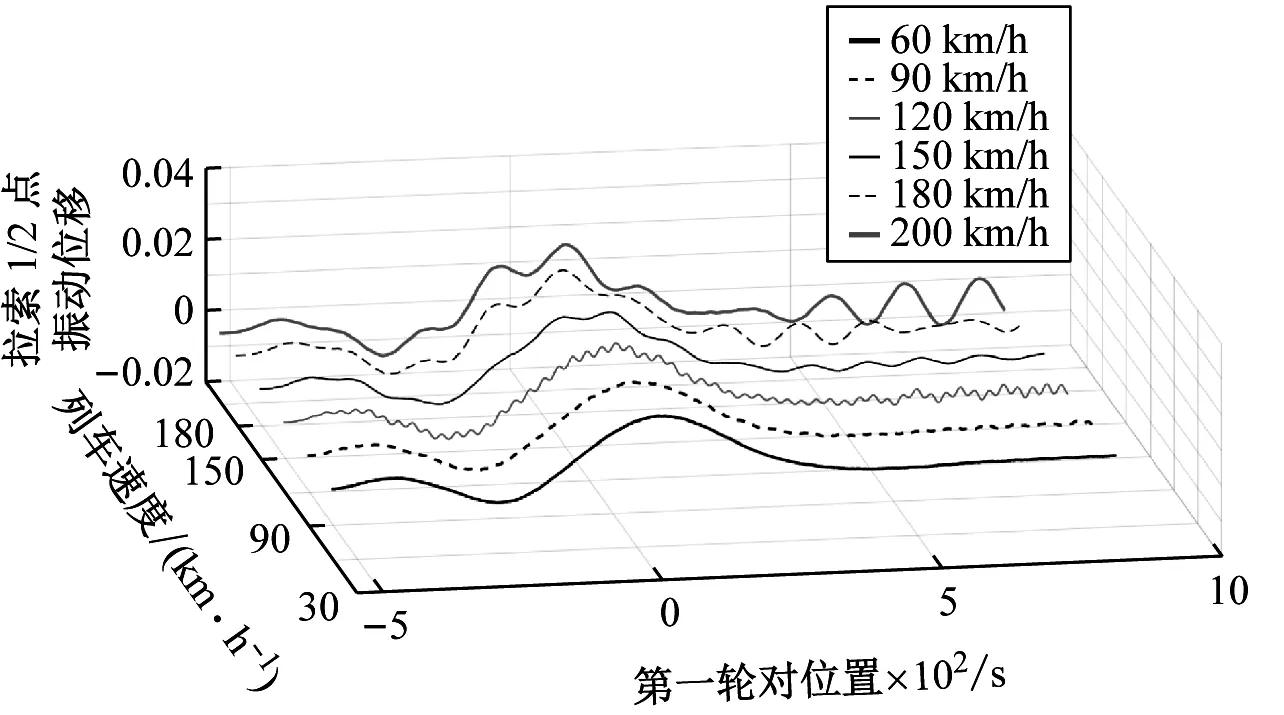
实际情况中单列车通过的情况最多，所以这里计算1列列车以不同速度(60 km/h～200 km/h)通过斜拉桥，拉索32的1/2点振动时程图如图31所示。

图31中，由于列车速度不同，所以X方向坐标是第一轮对运行距离，Y方向为不同速度取值，Z方向为拉索32的1/2点振动位移。 从图31可以看出，当列车速度提高以后列车的等效动力外激励频率有一定的提高，列车的动力冲击作用变大，拉索的振动幅值有一定的增加，但总的来说拉索的响应幅值较小、频率较低。

综上所述，本文研究结果表明，对于大跨度重载铁路斜拉桥，列车过桥更接近于一个静力过程，桥梁不会进入非线性振动状态，列车的动力作用不会达到本文第4节研究中导致拉索大幅振动的外激励条件。

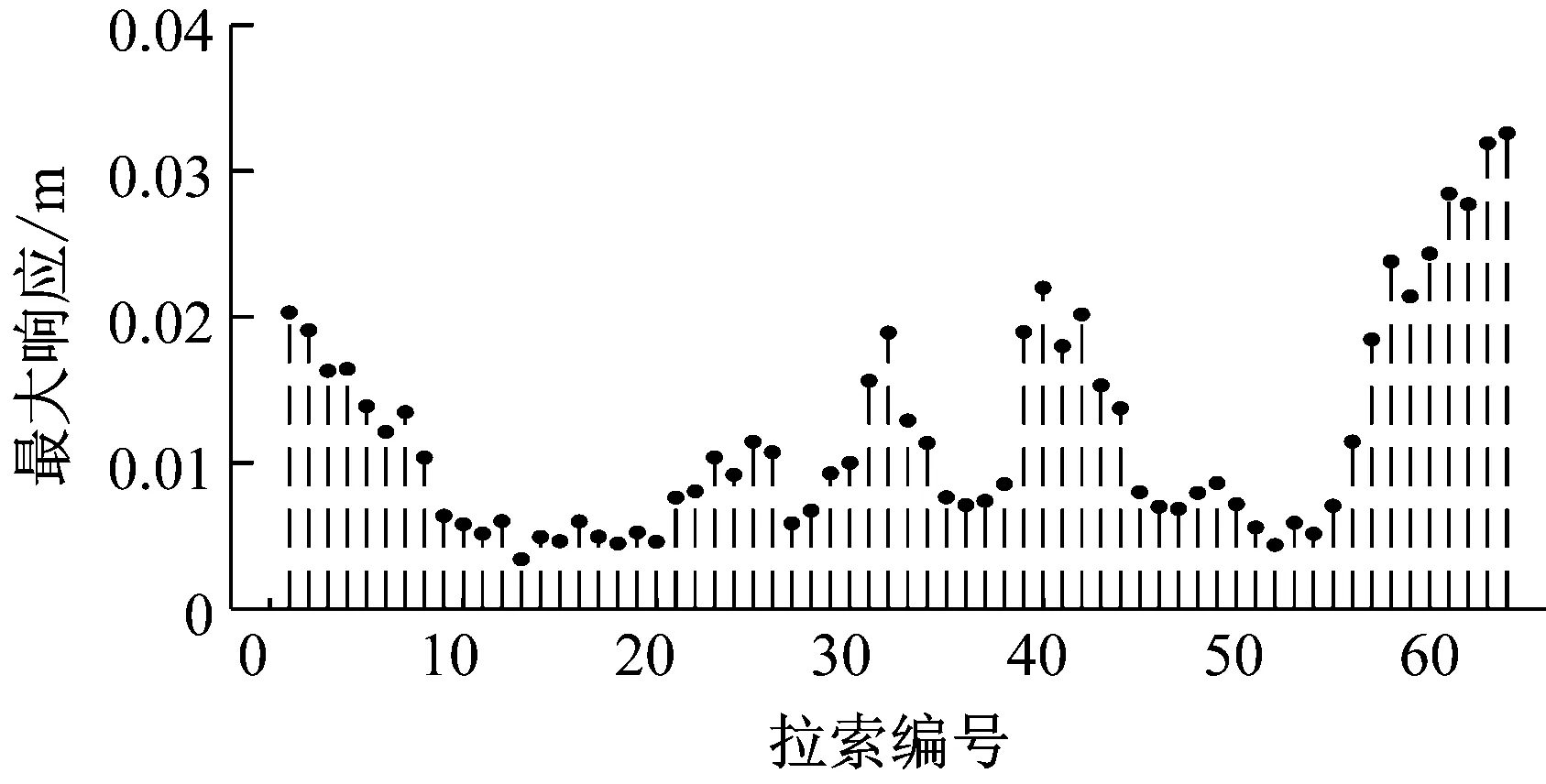
(a) 各个拉索最大响应

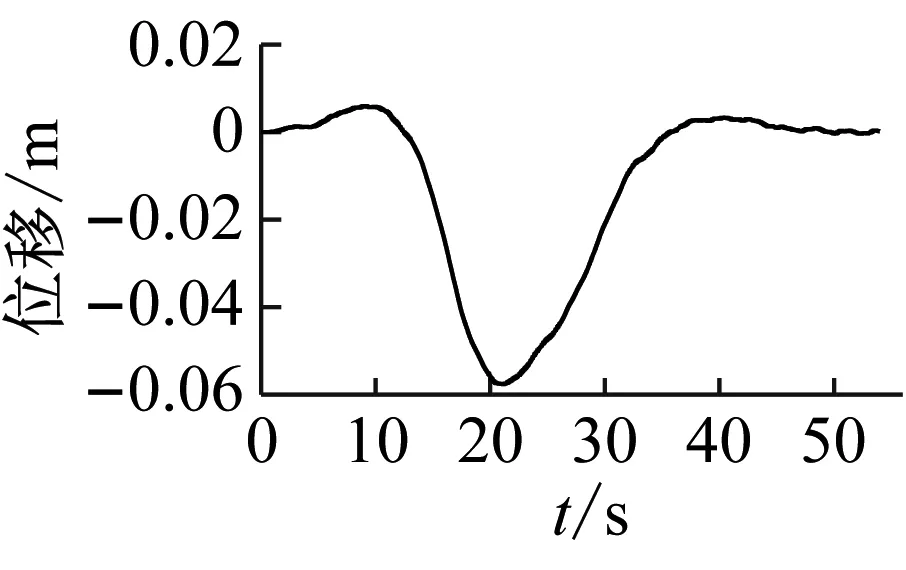
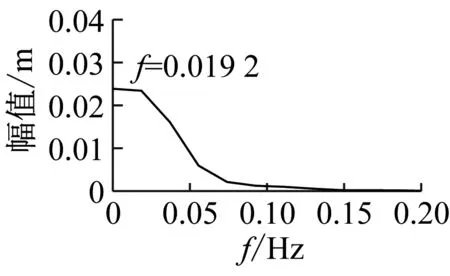
(b) 主梁跨中1/2点振动时程图、频谱图

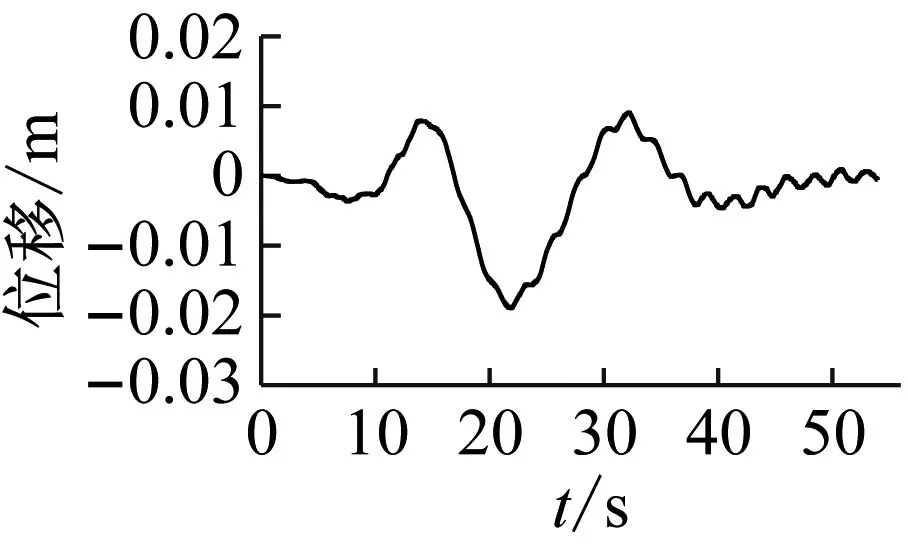
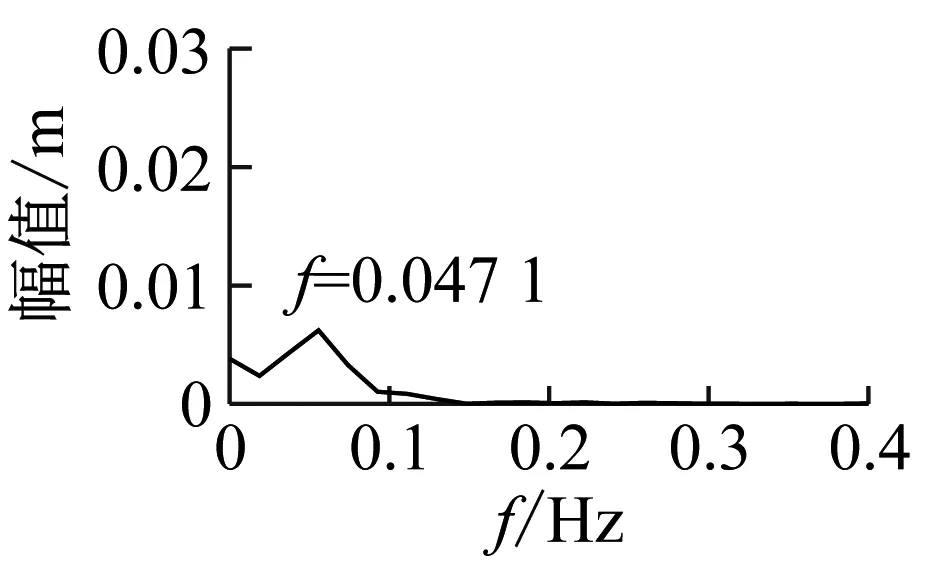
(c) 拉索32振动时程图、频谱图

图30 双车对开(v1=+120 km/h，v2=-90 km/h)主梁与拉索振动计算结果

Fig.30 Calculation results of vibration of the main girder and cable by two trains on opposite directions(v1=+120 km/h,v2=-90 km/h)

(a) emf图

(b) TIF图

(c) bmp图

图31 不同列车速度下拉索32的1/2点位移响应

Fig.31 The time-history curve of the 1/2 point of cable No.32 by a train at different speeds

4 结 论

本文通过建立算法与模型，针对天兴洲大桥进行了一系列的计算与分析，得到结论如下：

(1) 对于大跨度铁路斜拉桥，正常运营较难使结构进入明显的非线性振动状态。计算结果表明，全桥结构主梁跨中振幅达到约1.5 m的时候才会进入较为明显的非线性振动状态，这个振幅数值对于全长为1 100 m的大跨度斜拉桥系统来说，是弱非线性振动状态，但桥梁实际运营过程中显然不会出现1.5 m的振动幅度，所以使用线性动力时程积分计算结构在正常使用状态下的动力响应结果也是可靠的。

(2) 斜拉桥中索与梁振动的“相关”特性实际上是一个能量传递的过程。当斜拉桥上存在导致大幅索-梁相关振动的外激励时，外激励对斜拉桥系统注入能量，而能量通过主梁、桥塔传递到拉索上。具体的现象为：全桥结构振动时发生的索-梁相关振动导致某根拉索发生共振时，沿全桥分布的与之频率接近的拉索也会发生较大幅度振动，这种非线性振动类型通常为1∶1主共振，2∶1参数共振不容易发生。

(3) 当外激励作用位置在主梁上某拉索端点附近，激励频率与拉索1阶自振频率值接近2∶1的关系时，拉索容易发生2阶的1∶1主共振(短时间内振幅达到峰值)，而1阶2∶1参数共振不容易发生，但当激励持续时间较长时，拉索上2阶主共振与1阶参数共振可能同时发生。因此，在实际大跨度斜拉桥的分析中，可以只考虑拉索在索-梁相关振动作用下发生的1∶1主共振，不需考虑2∶1参数共振。

(4) 保持外激励幅值不变，外激励频率越高，激励位置越远离跨中、靠近桥塔，外激励越不容易使索-梁相关振动导致拉索发生大幅振动。因此，在实际分析中应当主要关注大跨度斜拉桥中跨和边跨最长拉索的索-梁相关振动情况。

(5) 研究表明，在一般情况下，列车对大跨度铁路斜拉桥的作用更接近一个静力过程，不会达到拉索大幅索-梁相关振动的外部激励条件(1∶1主共振、2∶1参数共振)。这说明，重载大跨度铁路斜拉桥由于其本身设计刚度较大，结构质量以及规模较大，列车不会导致斜拉桥发生大幅度的非线性索-梁相关振动。