基于RST-NMF模型的微震信号时频分析和识别

张法全， 王海飞， 王国富， 叶金才

(1.桂林电子科技大学 信息与通信学院，桂林 541004；2.广西无线宽带和信号处理重点实验室，桂林 541004)

近年来，微震监测技术凭借其有效的地压监测手段被广泛的应用于煤矿安全高效生产领域[1]。微震信号识别是微震监测技术的主要部分,微震信号属于典型的非线性、低信噪比信号[2-3]，其包含了岩石破裂信号、煤矿爆破信号、机械震动和其他施工噪声信号[4]。如何精确的识别微震信号是微震监测技术的关键问题。

目前，针对微震信号的处理主要采用傅里叶变换(Fourier Transform, FT)、小波变换(Wavelet Transform, WT)、S变换(S-Transform, ST)等时频分析方法[5]。江文武等[6]采用FT对大震级微震信号的频谱进行分析。Ma等[7-8]在FT的基础上进行小波切片和重构，弥补了FT的不足，唐守峰等[9]通过WT提取微震信号特征，为微震信号的模式识别打下了重要基础，朱权洁等[10]采用小波包与分形维结合提取信号特征，对微震信号做了初步识别，但是小波分析结果与基函数的选择紧密相关[11]。ST集成了短时傅里叶变换(Short-time Fourier Transform, STFT)和WT的优点，姜鹏等[12]将ST引入微震波信号识别领域，提取ST的能量分布特征进行分类，取得了较好的效果，但是该变换受到测不准原理的制约，其时频分辨能力有限。

非负矩阵分解(Nonnegative Matrix Factor, NMF)是一种新型的特征提取方法，可以得到原始数据的低秩矩阵[13]。传统的特征提取方法需要假设测量数据服从一定的分布[14-15]，如主成分分析(Principal Component Analysis, PCA)需要测量数据服从于高斯分布，独立成分分析(Independent Component Correlation Algorithm， ICA)能对非高斯数据进行有效处理，却对高斯数据的处理效果较差，而NMF算法对测量数据的性质仅有非负性的要求，能够有效处理高斯及非高斯分布的数据，且NMF分解得到的低维矩阵具有非负性和稀疏性，能够有效提取数据的局部特征和内在联系[16-17]，并在一定程度上抑制外界环境的干扰。

时频重排可以有效的聚集时频能量，提高时频分辨率[18]。本文将ST和时频重排相结合提出RST(Rearranged S Transform, RST)，以期达到在增强微震弱振幅信号的频域分量的同时又能提高时频分辨率。借用NMF技术分解时频矩阵，提取其分解量的宏观、微观统计量信息以期构造完备的特征空间，以期避免过拟合的发生。

1 RST-NMF理论

1.1 RST

由于ST对信号开窗分析，受到海森堡效应的制约，导致其时域分辨率和频域分辨率有限。本文将重排技术与ST相融合，在一定程度上聚集时频能量，提高时频分辨率，过程如下。

对于任意一个时变信号x(t)的S变换表达式如下

(1)

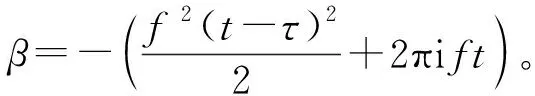
通过把某点(t,f)处的输出作为该点临近区域内能量分布重心处的输出，达到频谱在抑制交叉项的同时又提高了时频聚集性。

(2)

由帕塞瓦尔定理[19]和傅里叶变换的性质可将式(2)变换为式(3)

(3)

由此得到重排变换的算子如式(4)和式(5)

(4)

(5)

因此经过重排后的ST的表达式如下

(6)

1.2 NMF

NMF定义如下

(7)

式中，VN×M为待分解的N×M维非负矩阵，WN×r为分解基向量矩阵，Hr×M为分解系数矩阵。

NMF的实现过程实际上可理解为一个带约束的非线性的优化求解问题，本文基于欧几里得距离度量[20]，建立如下目标函数

(8)

通过迭代式(7)和式(8)可求解出WN×r、Hr×M

(9)

(10)

式中，WN×r反映了信号的频域特征，Hr×M反映了信号的时域位置特征。

2 算例分析

下面通过三道沟井田微震监测项目，测试RST-NMF算法在信号时频分析和特征提取的性能。

三道沟的地质特征属于典型的黄土丘陵沟壑地貌。浅层地质广泛分布第四系浅黄色黏土、亚黏土、粉沙、细沙层，底层偏松软；深层地岩主要为砂泥岩夹煤层，沉积较稳定，地层平缓，煤层埋藏浅。

根据实际地形情况，最终布置了12个传感器，使用圆形布阵如图1所示。

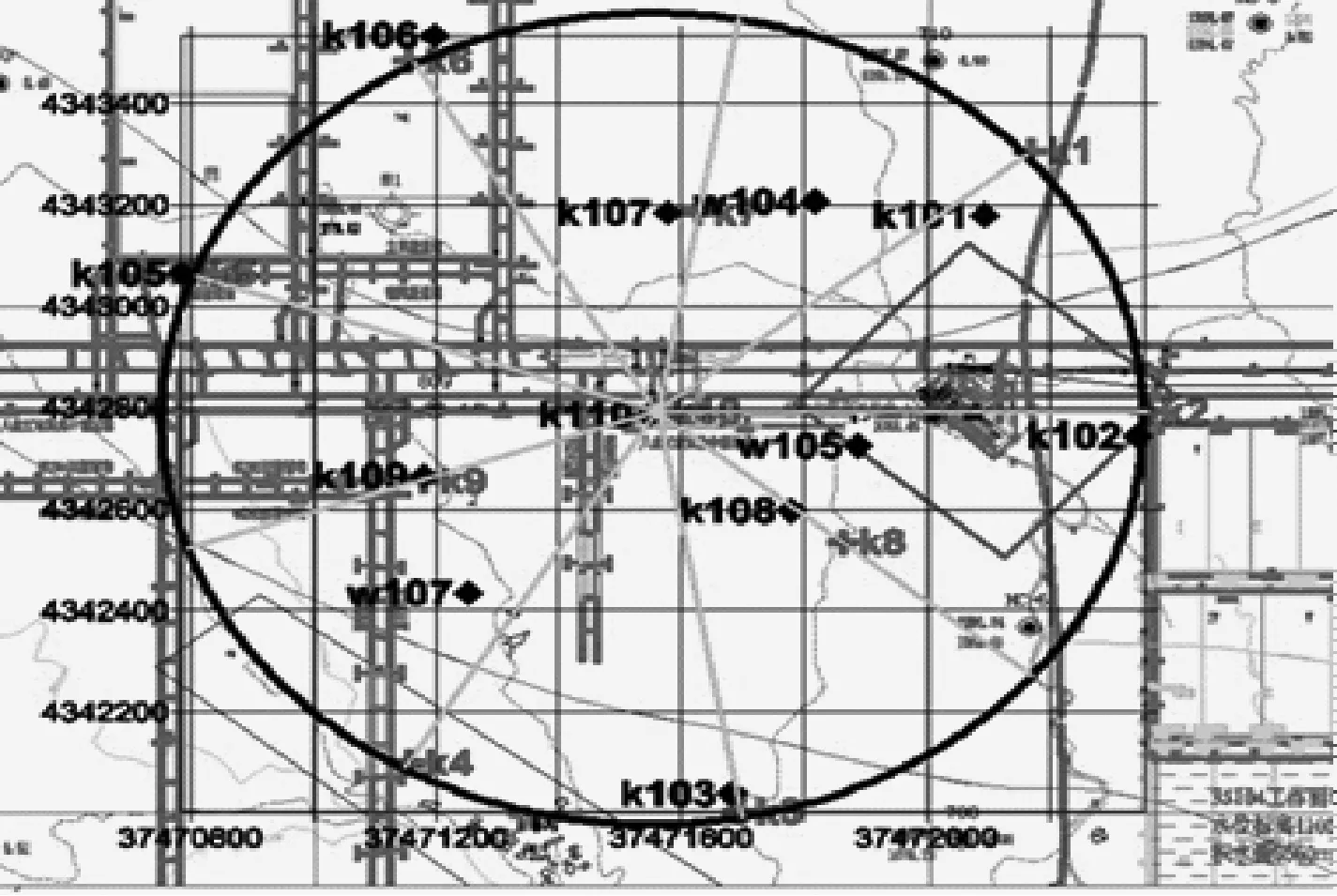
图1 基站检波器圆形布局图

2.1 基于RST的微震信号时频分析

从采集的微震信号中选取岩石破裂信号(图2(a))、爆破震动信号(图2(b))以及机械噪声信号(图2(c))为样本进行分析，其波形如图2所示。

(a) 岩石破裂信号

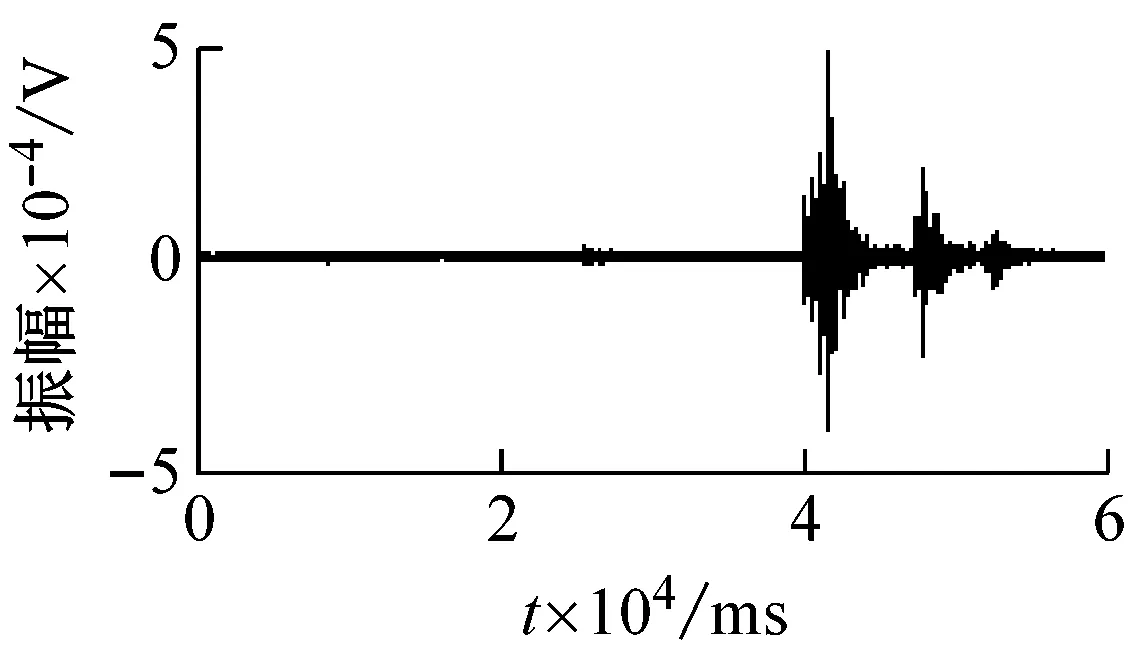
(b) 爆破信号

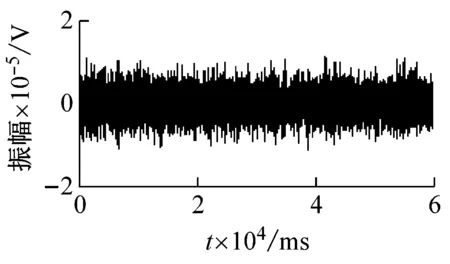
(c) 机械噪声信号

图2 信号波形

Fig.2 Waveforms of signals

由图2可知,震源不同，微震信号波形也不同。岩石破裂信号的振幅相对较大，是由于岩石受高应力发生形变和破断时，释放出大量弹性势能，且持续时间短。而爆破信号高频成分的吸收衰减相对严重，低频成分相对突出，一般伴随2～3个地震子波。机械噪声是由环境中的噪声生成的，因此持续时间较长，并且震幅较小且平稳。

对上述微震信号进行时频转换。为了显示RST变换的聚集性，这里同时进行ST对比。得到相应的时频图，如图3所示。

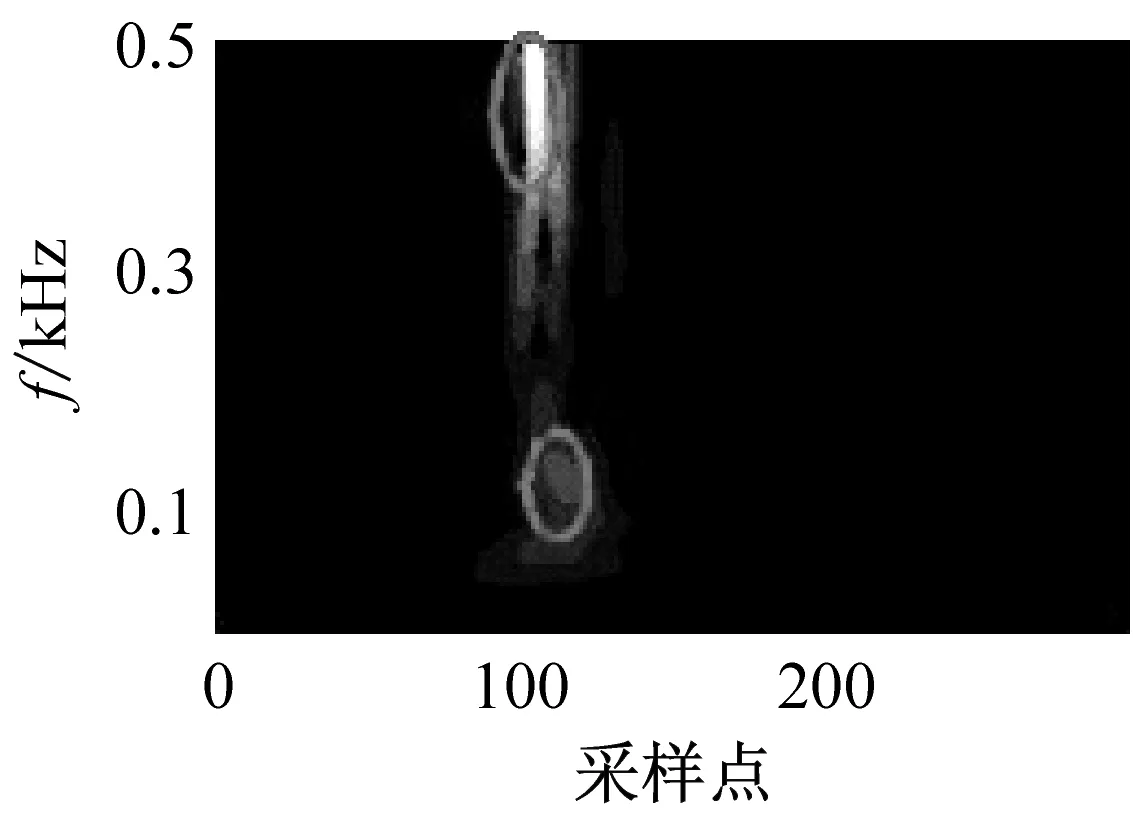
(a) 岩石破裂信号的ST谱

(b) 岩石破裂信号的RST谱

(c) 爆破信号的ST谱

(d) 爆破信号的RST谱

(e) 机械噪声的ST谱

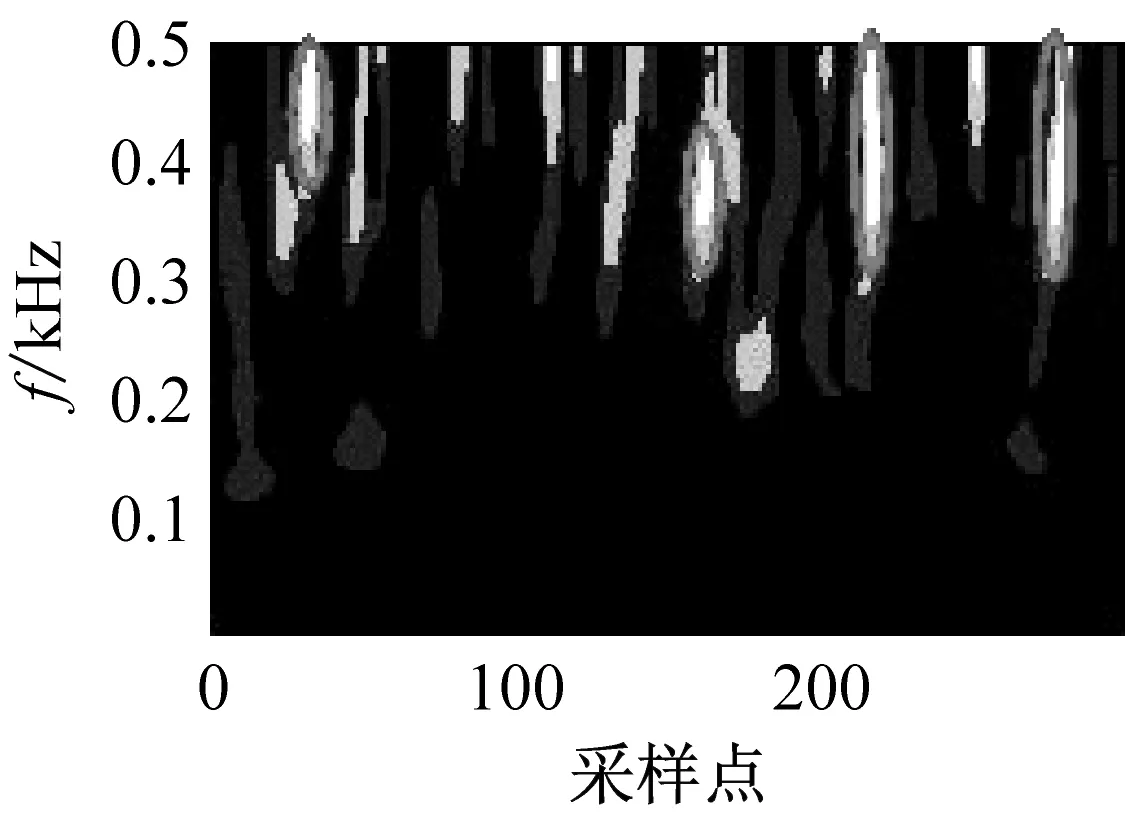
(f) 机械噪声的RST谱

图3 信号ST和RST

Fig.3 Signal time spectrum of ST, RST

在图3中，椭圆部分为微震信号时频能量的主要分布区域，可以看出RST的时频分辨率明显高于的ST时频分辨率。从整体上岩石破裂信号的时频谱比较单一，能量主要分布在[400,500]Hz高频区域，信号持续时间较短，大约30 ms。爆破信号的时频谱拥有明显的两个能量团，集中分布在[200,300]Hz之间，持续时间大约100 ms。机械噪声的时频谱比较丰富，分布于整个频带上并持续发生。

2.2 重排时频矩阵的NMF分解

利用NMF分解技术对微震信号的RST矩阵分解，得到相对应的分解基向量W和系数向量H，其分布特征如图4所示。

在图4中，1表示岩石破裂信号，2表示爆破信号，3表示机械噪声，w表示频域基向量，h表示时域位置向量。

由图4可知，岩石破裂信号持续时间较短，在50 ms左右，振幅较大，最大达到了20 mV，爆破信号的持续时间较长，大约有100 ms，振幅相对于岩石破裂信号较小，最大为7 mV，而机械噪声的持续时间较长，分布于整个时间轴上，但是其振幅较小且均匀，大约在2 mV。而系数矩阵的分布，并没有呈现明显的规律性。

2.3 提取特征

标准差用来反映一组数据的波动程度，其定义如下

(11)

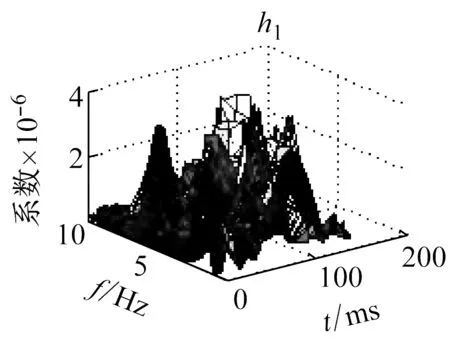
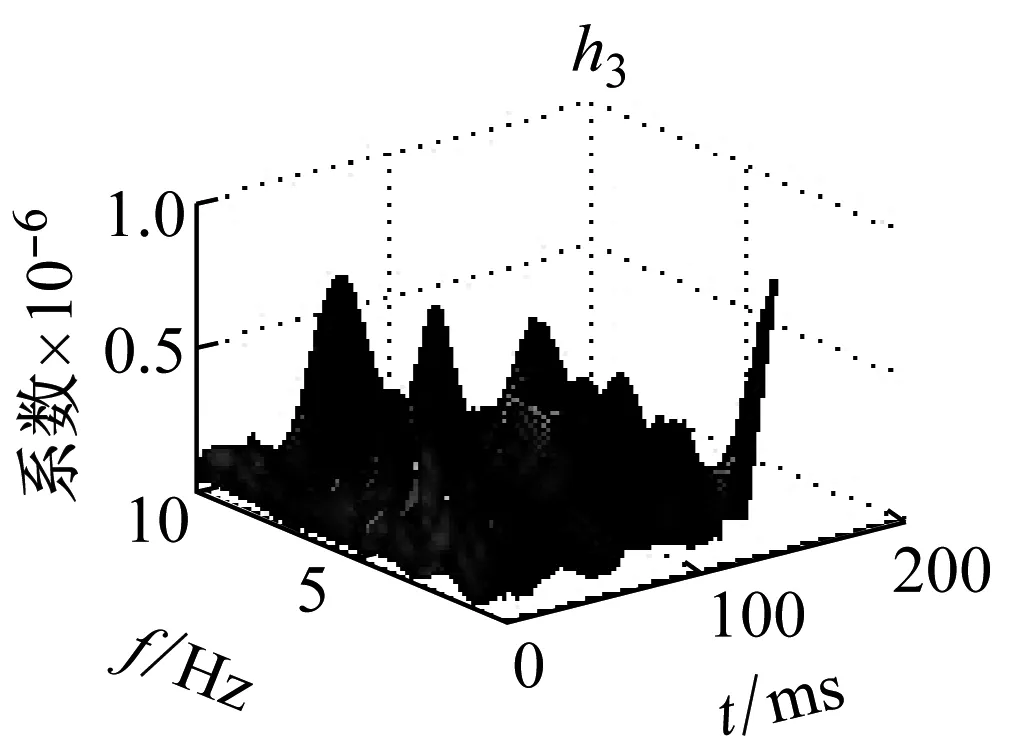
图4 分解向量分布图

Fig.4 Decomposition vector distribution

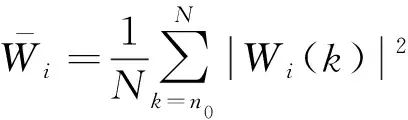
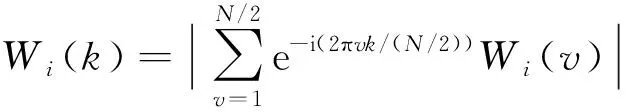
图5 标准差

由图5我们可以明显看到,岩石破裂信号的频域基向量的波动程度在整体上大于爆破信号的波动程度，爆破信号的波动程度又明显大于机械噪声的波动程度。岩石破裂信号和爆破信号存在明显的极值点，极小值分别为0.75 mV2/s，0.25 mV2/s，极大值点分别为2 mV2/s，1.1 mV2/s。岩石破裂信号时域位置向量的标准差和爆破信号的波动程度相当，但都大于机械噪声的波动程度，机械噪声的波动值较小接近于0，说明机械噪声的时域位置向量基本平稳。

WN×r的相关系数反映一组数据中相邻元素之间的相关性

(12)

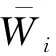
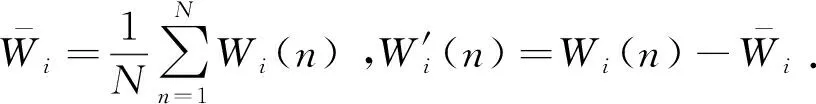
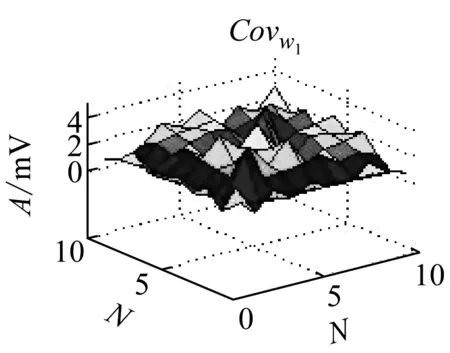
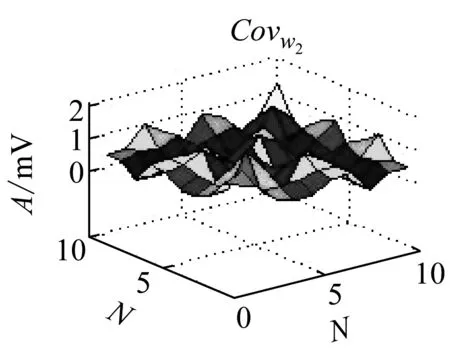
图6 相关系数

Fig.6 Coefficient of association

在图6可知，可以看出岩石破裂信号的相关性分布较均匀且基本大于1，说明岩石破裂信号的相邻时刻元素之间的变换存在较强的相互关系，相关系数在[1,3]之间,爆破信号的相关系数集中在[-0.5,1.5]之间，机械噪声的相关系数在[0,0.3]之间，相关性较小。

导数反映一组数据的变化趋势

(13)

其分布如图7所示。

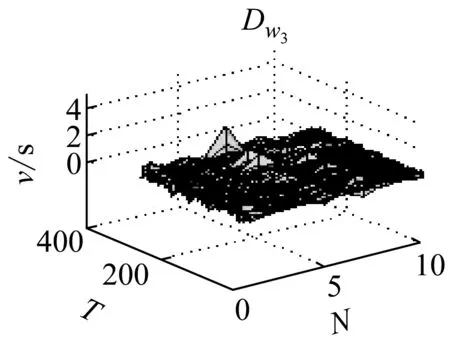
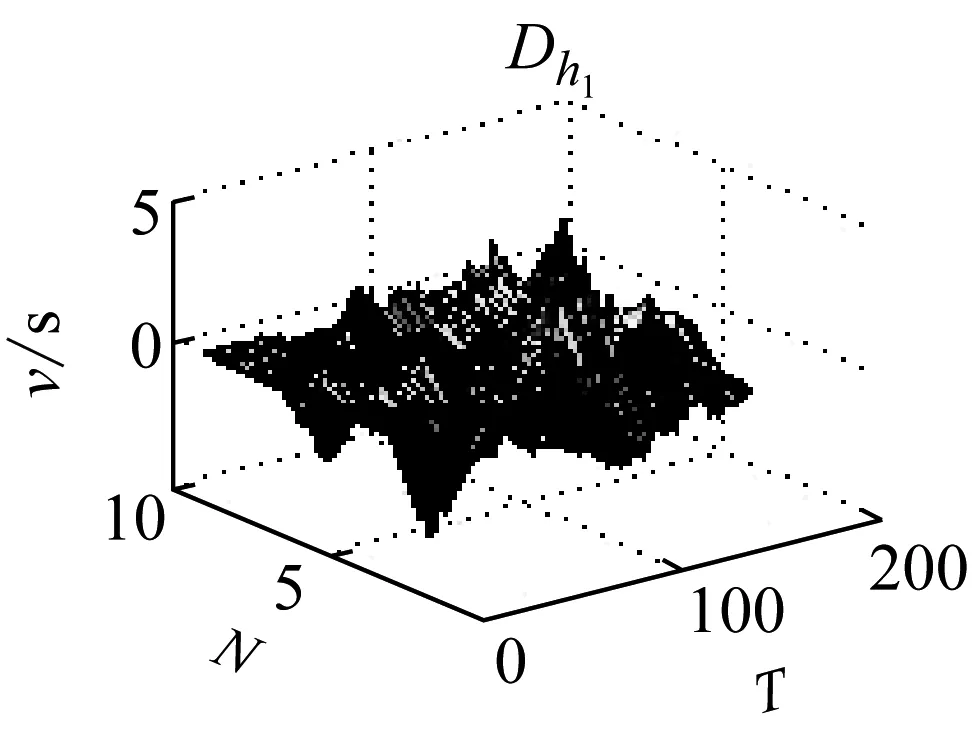
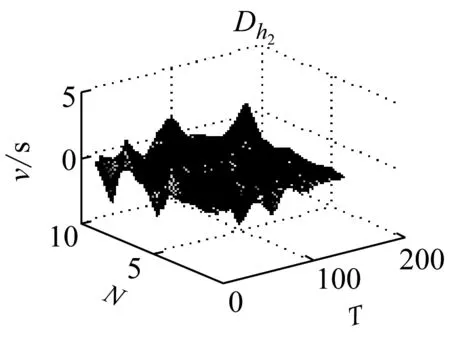
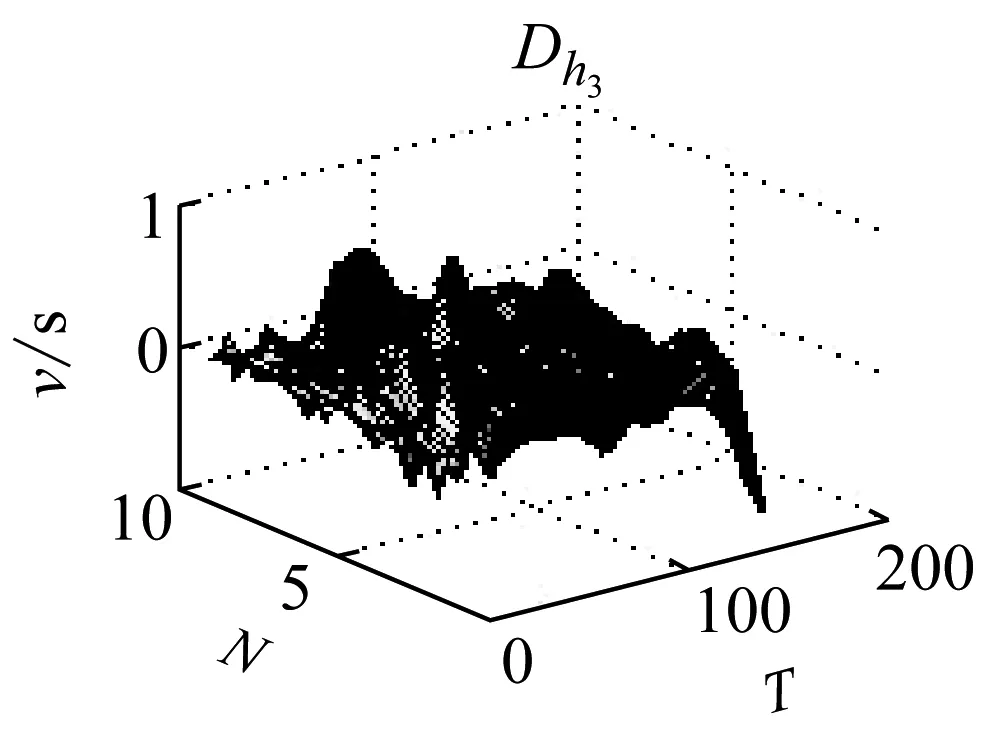
图7 导数

Fig.7 Derivative

由图7可以很明显看出,Dw1在岩石破裂信号的发生的区域导数的变换比较急剧，这是由于岩石破裂信号是受剪切型应力作用的结果，Dw2导数分布呈现缓慢变换的趋势，这是由于爆破信号发生的受介质传播的影响，持续时间长，且产生子波。而机械噪声的导数基本稳定在零附近，说明机械噪声比较稳定。

稀疏度：

(14)

式中，M为hi的长度。

综上所述，从每个频域基向量Wi中提取标准差SDwi、协方差Covwi、导数Dwi三个特征向量，从每个时域位置向量Hi中提取标准差SDhi、稀疏度SPhi两个特征向量。构造特征空间如下

F=(SDwi,Covwi,Dwi,SDhi,SPhi,…)

(15)

式中,下标wi说明为第i个频域基向量的特征，其中i=1,2…N。

2.4 震信号多类分类SVM模型

为了将该算法具有更广阔的工程应用，本文采用支持向量机(Support Vector Machine, SVM)把微震信号分为岩石破裂信号、爆破信号和机械噪声信号三类，对应的分类标签为1、2、3。图8为本文的分类器模型。

由图8可知，针对微震信号的分类步骤如下：

步骤1 对已知微震信号进行重排ST；

步骤2 对步骤1得到的结果进行NMF分解；

此次网格化管理试点在原来基础上加以改进，以前社区网格化成员是由社区里面的工作人员下网格，他们既要完成自身的工作还要承担网格里的工作，导致分身乏术，两边工作都无法兼顾。 本次网格化管理是区里面统一从社会上招聘专门的人员，分配到各个社区，工作归各个社区管理，档案工资等人事方面归街道管理。 刚开始试点两个月多月，书记表示如果此次网格化试点运行顺畅，确实能够帮社区减清一些负担。

步骤3 步骤2中得到的结果提取标准差、导数、稀疏度、相关系数等信息统计量构造特征空间；

步骤4 采用自助法[21]选择训练样本和测试

图8 分类器模型

样本；

步骤5 训练模型得出分类标签。

2.5 不同时频变换方法的识别结果

下文在分类识别中均采用SVM分类器，Gauss核函数，惩罚参数C=2，Gauss核宽度γ=1。分类结果的优劣，沿用文献[5,8]中以

准确率=识别正确总数/样本总数为标准。

为了测试RST变换的优越性，本文选取ST的时频分析方法对比，分类结果如表1所示。

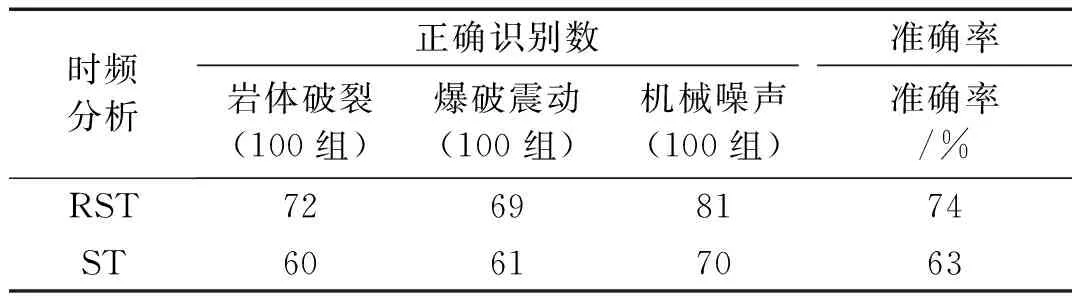
表1 不同时频变换方法的分类结果

2.6 不同分解方法的识别结果

为了证明RST-NMF的优越性，本文分别采用局部特征尺度分解法 (Local Characteristic-scale Decomposition, LCD)[22]、局部均值分解法(Local Mean Decomposition, LMD)[23]方法对比，分类结果如表2所示。

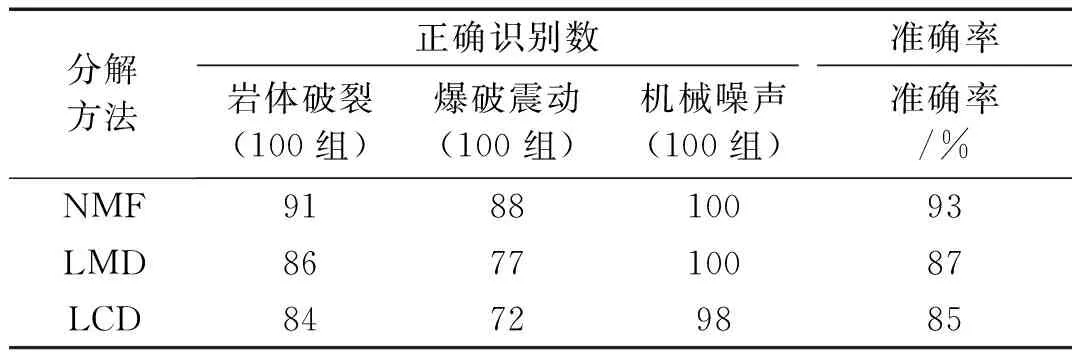
表2 不同分解方法的分类结果

由表2可知,RST-NMF方法的准确率高于LMD、LCD，这是由于LCD、LMD的自适应分解存在端点效应、模态混叠等问题，降低了信号的保真度，导致在分类时存在过拟合的问题，总体来说RST-NMF识别效果较优。

2.7 不同特征空间的识别结果

为了证明特征空间F的优越性，本文选取常用的特征空间相关系数Cov、能量谱系数ECov对比，结果如表3所示。

表3 不同特征空间的分类结果

由表3可知：特征空间F的识别正确率大于Cov、ECov识别正确率，即F包含了更多微震信号的特征信息。

3 结 论

本文针对微震弱振幅信号难以识别的问题，提出了RST-NMF的时频分析和特征提取算法得出如下结论：

(1) RST时频分析方法，对频域分散的能量团有很好的聚集性，增强微震弱振幅信号的时频分辨率。

(2) 时频矩阵经NMF分解最大程度上获取微震信号的局部特征和内在联系，并在一定程度上抑制外界环境的干扰。

(3) 提取NMF分解向量的宏观和微观统计量标准差、导数、稀疏度、相关系数，保证了提取的信号特征空间集完备性，可以有效避免分类时欠拟合的发生。