自动导航小车制动能量回收控制策略研究

张 捷，张绪鹏，王书亭

(1.华中科技大学 能源与动力工程学院，湖北 武汉 430074；2.华中科技大学 中欧清洁与可再生能源学院，湖北 武汉 430074；3.华中科技大学 机械科学与工程学院，湖北 武汉 430074)

自动导航小车(automated guided vehicle, AGV)是自动化仓储系统的关键设备[1]，是连接物流和生产的重要桥梁，代替人工进行物料搬运的移动工作台，可有效提高制造企业的生产效率，降低生产成本。AGV一般以蓄电池作为动力源，充电时间长、单次行驶里程短等问题严重制约了其工作效率。再生制动系统是电动汽车中的一项技术[2]，其作用是将车辆制动时的动能经过再生制动系统转换成电能，储存到储能单元中，达到提高整车能量利用率和增加续驶里程的目的。在这个过程中，电机处于发电模式，产生电能给电池充电，同时在电机中产生制动力矩，实现车辆制动[3-4]。目前对AGV的研究大多侧重于智能化方向，对其能量利用率方面的研究较少，因此笔者将再生制动技术应用于AGV，对当前的制动能量回收控制策略进行分析优化，以提高AGV能量回收率。

1 AGV整车仿真模型

1.1 建立AGV整车模型

ADVISOR软件是由美国可再生能源实验室在Matlab和Simulink软件环境下开发的高级车辆仿真软件[5]，该软件可对传统汽车、纯电动汽车和混合动力汽车的各种性能作快速分析。ADVISOR采用了以后向仿真为主、前向仿真为辅的混合仿真策略，集成了两种方法的优点，既使得仿真计算量较小，运算速度较快，又保证了仿真结果的精度。

在ADVISOR仿真软件中原有电动汽车模型的基础上搭建AGV整车模型。实验室搭建的AGV平台如图1所示，AGV整车参数如表1所示。小车行驶所需动力通过电机传递到单级减速器，最后传递到车轮轴，AGV平台采用的驱动电机是协盛达V7系列永磁同步伺服电机，其具有功率范围大、最高转速低的特点，适用于低速平稳的运动控制，单级减速器传动比为2.2。

图1 实验室搭建的AGV平台

部件参数名称参数值整车尺寸(L×W×H)/mm1 500×1 000×650质量/kg500轴距/mm1 100质心高度/mm350车轮半径/mm140电机质量/kg25额定功率/kW6.25电池质量/kg55额定电压/V51.1容量/Ah144(1.0C)

在ADVISOR软件中建立的AGV整车顶层模型如图2所示，图中从左向右的箭头表示后向仿真，向上级模块传递转矩、车速等需求信息；从右向左的箭头表示前向仿真，向下级模块传递实际能提供的转矩、车速等信息。

1.2 建立AGV四轮驱动模块

笔者以四轮驱动的AGV为研究对象，然而ADVISOR中所有默认车型都是前轴驱动的形式，因此需要对其进行二次开发，以满足AGV仿真要求。通过对AGV进行受力分析，建立其动力学模型并求解动力学方程组，应用Matlab/Simulink平台建立AGV的四轮驱动仿真模块。AGV受力分析如图3所示。

图2 AGV整车顶层模型

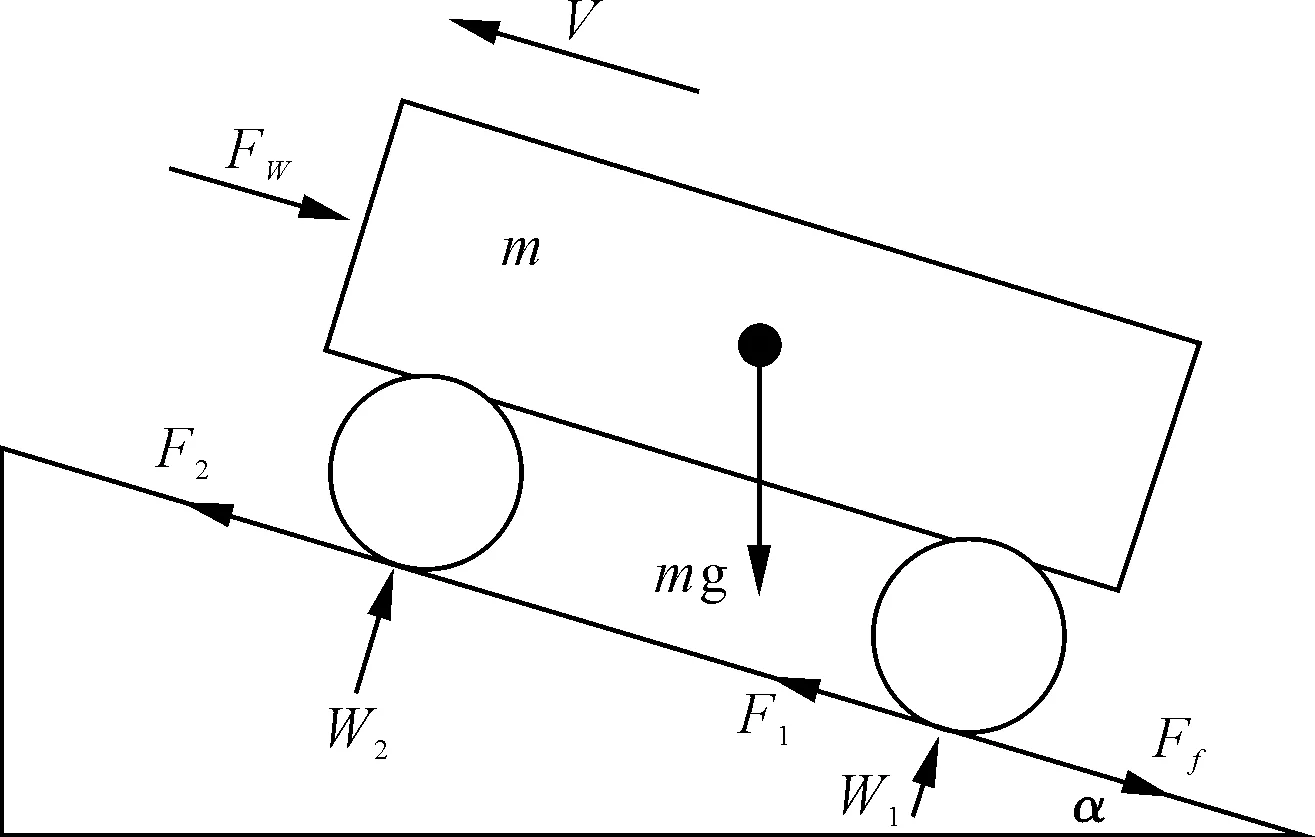
图3 AGV受力分析图

由图3可知，假设小车此时处于驱动附着极限的状态，小车在坡度为α弧度的路面上行驶，初始速度为V0，在极限附着力Fmax的驱动下所能产生的最大末速度为Vt，根据力的平衡方程可以得到：

Fmax-Fw-Ff-Fα=ma

(1)

式中：Fw为空气阻力；Ff为滚动阻力；Fα为坡度阻力；m为小车质量；a为加速度。

极限附着力Fmax的表达式为：

Fmax=F1+F2=W1μmax+W2μmax=mgμmaxcosα

(2)

式中：F1、F2分别为小车前、后轮驱动力；W1、W2分别为地面对小车前、后轮的支持力；μmax为最大附着系数。

空气阻力Fw的表达式为：

(3)

式中：ρ为空气密度；Cd为空气阻力系数；A为车辆迎风面积；Vave为迭代步长内的平均速度，Vave=(Vt+V0)/2。

滚动阻力Ff的表达式为：

Ff=mg(f1+f2Vave)cosα

(4)

式中：f1、f2分别为计算滚动阻力系数时的截距与斜率，滚动阻力系数等于f2与迭代步长内的平均车速的乘积再加上f1。

坡度阻力Fα的表达式为：

Fα=mgsinα

(5)

迭代步长内的加速度a的表达式为:

a=(Vt-V0)/t

(6)

式中：t为仿真迭代步长。

将式(2)～式(6)代入式(1)中可得AGV在附着极限时迭代步长末的速度计算公式，如式(7)所示。当小车处于制动工况下的附着极限时，Fmax为制动力，方向相反，其他受力情况与驱动时相同，此时Fmax=-mgμmaxcosα，将其代入式(1)可得制动工况下达到极限附着时最小车速的计算公式，如式(8)所示。

根据上述极限附着状态下的极限车速，对AGV整车模型进行修改，利用Matlab/Simulink工

(7)

(8)

具建立四轮驱动仿真模块，如图4所示。将该模块导入到AGV整车模型中进行仿真验证，确保其能够正确运行。

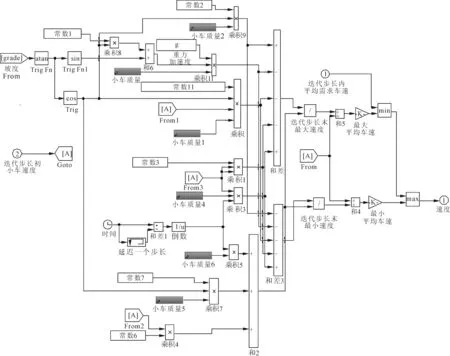
图4 AGV四轮驱动仿真模块

1.3 AGV整车仿真模型验证

为了验证建立的AGV整车模型的有效性，笔者进行了AGV动力性仿真，并与实车测试结果对比，结果如表2所示。由表2可知，模拟值与测试值的误差在理想范围内，表明所建立的AGV整车模型可以满足仿真的需要。

2 基于模糊控制的再生制动控制策略

2.1 线性查表法再生制动控制策略分析

在制定制动能量回收策略时，汽车前后轴的制动力分配、再生制动与摩擦制动之间的分配是需要着重考虑的两大问题[6-7]，这关系到汽车制动时的安全性、稳定性，同时也会影响制动能量的回收效果。目前，各电动汽车厂家常用的再生制动控制策略为线性查表法[8]，该策略直接根据实际车速采用查表的方式来实现制动力分配，即通过查表求得再生制动力和前轮摩擦制动力，剩余的制动力由后轮摩擦制动力提供，其制动力分配系数如图5所示。

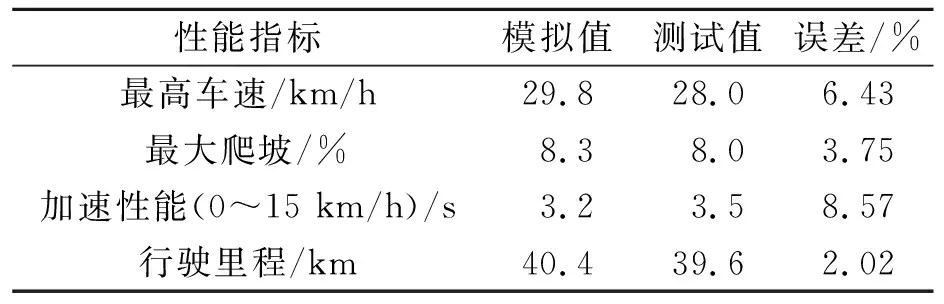
表2 AGV动力性参数仿真与测试结果对比

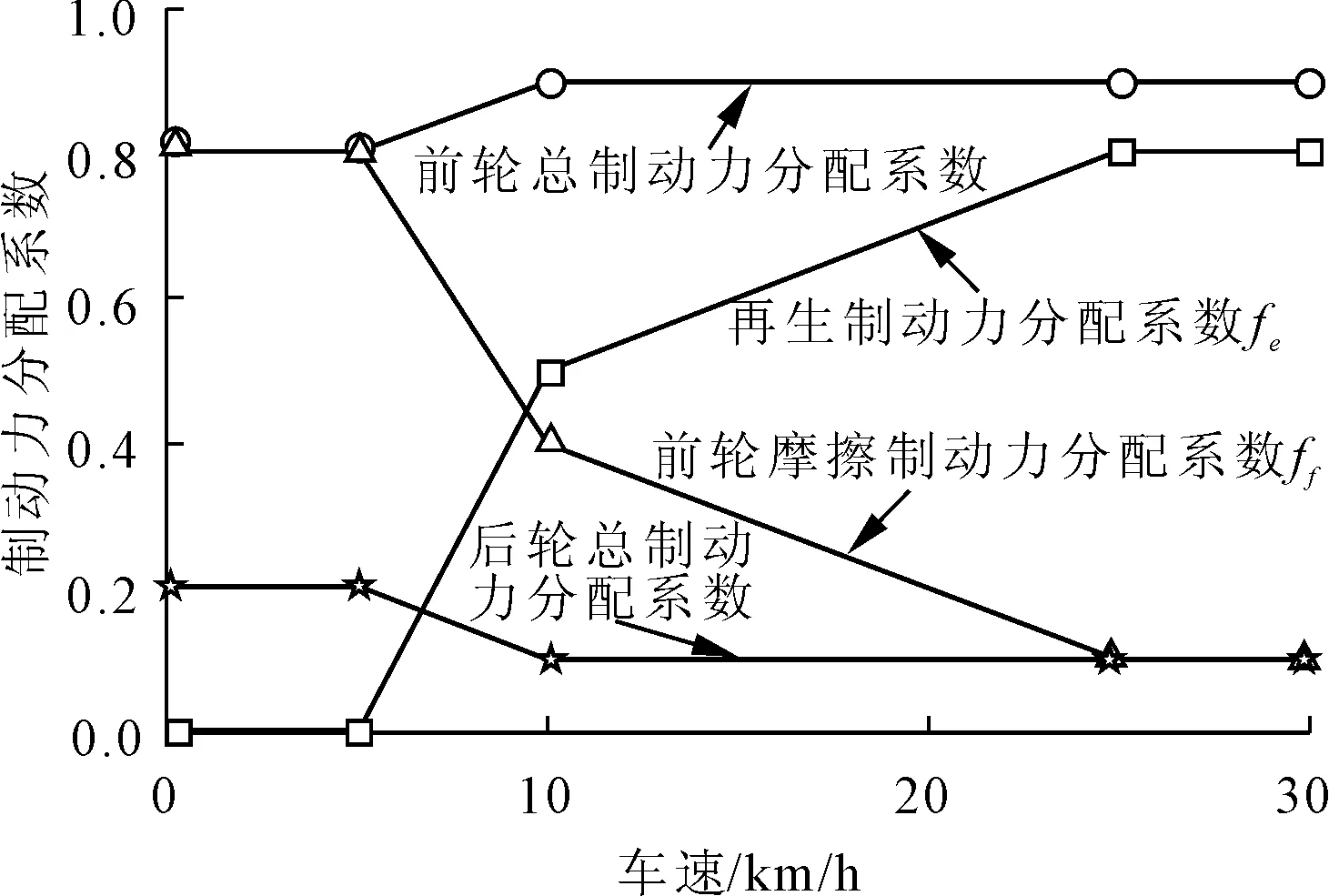
图5 线性制动力分配系数

由图5可知，该分配系数通过车速查表获得，随着车速的增大，再生制动力所占比例也随之增加，前轮摩擦制动力所占比例随之减小。这种控制策略简单可行，可在一定程度上实现能量回收[9-10]，但没有考虑其他因素对能量回收的影响，比如制动强度、电池电量等。此外，AGV实际运行工况比较复杂，很多参数都在不断变化，需要对其制动过程进行更深入的分析，制定更加有效的再生制动控制策略。

2.2 基于模糊控制的再生制动控制策略

在小车制动过程中，制动力的分配受到很多因素的影响[11-12]，如电池荷电状态(SOC)、小车的制动强度、车速等。综合考虑多个因素，设计了基于模糊控制的制动力分配策略，实现对制动力更加合理的分配。

模糊控制器采用三输入单输出的结构，输入变量为车速V、电池SOC、制动强度z，输出变量为再生制动分配系数K。采用极小(NB)、小(NS)、中(M)、大(PS)、极大(PB)5个模糊语言变量来描述输入、输出变量。论域是模糊控制器进行隶属度计算的基础[13-14]，模糊论域的设计如下：AGV车速V的实际范围为[0，30]，取其论域为[0，3]；电池SOC的实际变化范围为[0，1]；制动强度z的实际变化范围为[0，1]；再生制动强度分配系数K的实际变化范围为[0，1]，因SOC、z、K的范围较小，所以直接把真实值范围作为它们的论域。输入、输出变量的取值需要通过尺度变化的量化因子映射到对应的论域中，量化因子可通过式(9)计算：

(9)

式中：[xmin，xmax]为输入量的实际变化范围，[ymin，ymax]为所设定的论域的范围。由此可得，车速V的量化因子为0.1，其余变量的量化因子均取为1。

三角形隶属度函数计算简单，性能良好，因此选择常用的三角形隶属度函数作为全部输入、输出变量的隶属度函数，模糊控制器选用Mamdani型，利用Matlab模糊控制工具箱对模糊控制器进行设计。

通过隶属度函数对变量进行模糊化处理之后，需要根据模糊规则判断每种情况所采用的策略，模糊规则的制定是模糊控制的核心内容，控制性能的好坏很大程度上由模糊规则决定，生成的控制规则曲面越光滑平稳，控制效果越好。模糊规则的设计需要综合考虑各个输入变量对输出变量的影响，其设计原则为：①当电池SOC值较高时，为避免电池过充，应当减小再生制动所占的比例，即减小再生制动分配系数K；相反，当电池SOC值较低时，在满足制动安全性的前提下，应当增大再生制动所占的比例，即增大再生制动分配系数K。②当紧急制动或制动强度z较大时，应当减小再生制动所占比例，以摩擦制动为主，避免危险发生；当制动强度z较小时，应当增大再生制动分配系数K，以发挥再生制动系统的作用，增大能量回收。③当车速V过低时，受电机自身工作特性的影响，再生制动系统可提供的反向电动势较小，难以为电池充电，且此时无法提供足够的制动转矩，应当减小再生制动所占的比例；当小车在车速V较大的工况下进行制动时，再生制动系统能够产生较大的充电电流，同时提供较大的制动转矩，但是为了保证小车在高速工况下制动的安全性，此时应同时考虑制动强度对制动力分配的影响。

对于设计的三输入单输出的模糊控制器，其控制规则采用“ifSOC, andV, andz, thenK”的方式，即综合考虑电池SOC、车速V和制动强度z3个因素对制动力分配系数进行计算。例如，如果电池SOC小(NS)，车速V中(M)，制动强度z小(NS)，则取K为大(PS)，以提高再生制动所占比例，增大能量回收。由于输入、输出变量都有5个模糊子集，基于上述规则，可制定出由125条模糊语句构成的模糊规则。

利用Matlab/Simulink工具搭建制动力分配仿真模型，前后轴制动力分配采用固定比例分配策略，摩擦制动力和再生制动力分配采用模糊控制策略。因为ADVISOR采用了后向仿真为主、前向仿真为辅的混合仿真方法，所以需要分别建立前向、后向制动力分配仿真模型，前向仿真模型如图6所示，后向仿真模型如图7所示。再生制动力分配系数K由模糊控制策略根据电池SOC、车速V、制动强度z推理得到，将再生制动控制策略模型导入到ADVISOR软件中，嵌入AGV整车模型中进行仿真分析。

图6 前向仿真制动力分配模型

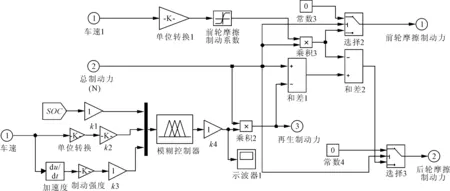
图7 后向仿真制动力分配模型

3 仿真结果及分析

为验证模糊控制策略的有效性，在没有典型AGV运行测试工况的前提下，根据AGV急起急停、频繁启停的运行特点，设计了“CYC_ECE_AGV”和“CYC_NYCC_AGV”两种行驶工况。“CYC_ECE_AGV”工况如图8所示，该工况主要考虑AGV在不同工位间不断行驶、启停的特点。“CYC_NYCC_AGV”工况如图9所示，该工况是参考纽约城市循环工况“CYC_NYCC”所设计，并将其车速减小为原来的1/2，以符合AGV运行特点。两种仿真工况的具体参数如表3所示。

图8 CYC_ECE_AGV行驶工况

图9 CYC_NYCC_AGV行驶工况

参数循环工况CYC_ECE_AGVCYC_NYCC_AGV行驶距离/km1.790.95最大速度/km/h20.0022.29平均速度/km/h10.355.70最大加速度/m/s20.691.34最大减速度/m/s2-0.69-1.32平均加速度/m/s20.690.31平均减速度/m/s2-0.69-0.30时间/s621598停车次数2318

AGV的续驶里程和电池SOC可以很直观地反映小车的性能，因此，利用电池SOC的变化情况和小车行驶里程对仿真结果进行直观对比。利用ADVISOR软件对模糊控制策略和线性控制策略在两种工况下进行仿真对比，“CYC-ECE-AGV”工况下电池SOC的仿真结果如图10所示，“CYC-NYCC-AGV”工况下电池SOC的仿真结果如图11所示。

图10 CYC_ECE_AGV工况下电池SOC曲线

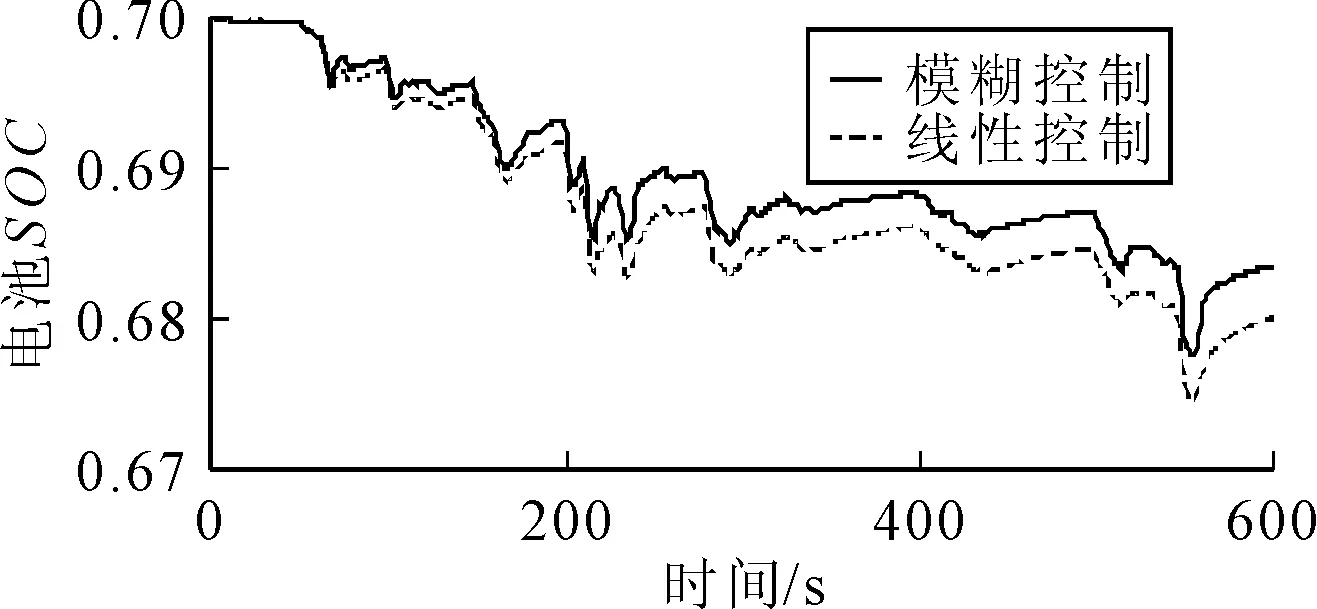
图11 CYC_NYCC_AGV工况下电池SOC曲线

由图10和图11可知，基于模糊控制的电池SOC曲线和线性查表法的电池SOC曲线下降趋势基本相同。在不同循环下，当车速下降时，SOC曲线都有明显的上升，说明控制策略起到了回收制动能量的作用，并且模糊控制策略的SOC曲线下降速度明显比线性查表法的SOC曲线下降速度慢，可以直观地验证模糊控制策略的优异性。SOC精确的变化值如表4所示，并用式(10)评估SOC提升率。

(10)

表4 电池SOC仿真结果对比

式中：SOC0为初始状态时电池SOC的值；SOC1、SOC2分别为在不同控制策略下终止时刻电池SOC的值。

由式(10)可得在仿真结束时不同控制策略下电池SOC变化率，如表5所示。

表5 电池SOC变化率对比

对AGV行驶里程进行仿真，对比小车在无能量回收时的行驶里程结果，可以得到行驶里程提升量，具体结果如表6所示。

表6 AGV行驶里程结果对比

由表5可知，在“CYC_ECE_AGV”工况下，仿真结束时模糊控制策略的电池SOC值比线性查表法的SOC值提高21.25%，比无能量回收的SOC提升41.71%；在“CYC_NYCC_AGV”工况下，仿真结束时模糊控制策略的电池SOC值比线性查表法的SOC值提高16.24%，比无能量回收的SOC值提高31.82%，表明模糊控制策略可以有效提高制动过程中的能量回收率。由表6可知，模糊控制策略比无能量回收时的行驶里程提高了17.7 km，里程提升率约为43.81%，极大提高了AGV行驶里程。

4 结论

以自动导航小车及其制动系统为研究对象，设计了基于模糊推理的制动能量回收控制策略，在ADVISOR软件中对AGV进行仿真分析，得出以下结论：①与传统线性控制策略相比，模糊控制策略可以显著提高制动过程中的能量回收，使电池SOC最大可提升21.25%，与无能量回收相比，电池SOC最大可提升41.71%，行驶里程提升17.7 km。②仿真工况的设计对能量回收的效果有较大的影响，主要是因为行驶工况中的车速、制动次数、制动强度等因素对制动力分配产生了较大影响。③研究结果证明了将再生制动系统应用于AGV的必要性与可行性，AGV在车间的行驶工况具有启停频繁的特点，每天启停高达2 000次以上，所以在AGV上加入制动能量回收系统，可以有效提高能量利用率，提升AGV的行驶里程和工作效率。