完善认知结构 发展核心素养——以“多元二次变量的最值问题”教学活动设计为例

(金华第一中学,浙江 金华 321015)

在高三数学复习阶段，笔者常听到教师抱怨：一听(教师讲解)就懂，一看(参考解答)就会，一做(练习或试卷)就错.近日，笔者所在学校为了促进高三教学质量的提升，邀请了浙江省金华市教研室的教研员来校进行专题教研，在与学生代表座谈时，有学生坦言：知识都知道，分数拿不到.这句话既道出了学生学习数学的困惑，又真实地反映了教师教学面对的学情.“如何帮助学生提高解题能力,课堂教学怎样落实数学核心素养”是值得每位数学教师思考的问题.

1 以问题解决为导向，完善认知结构

问题解决是以思考为内涵、以问题目标为定向的心理活动或心理过程.现代认知学派认为：问题解决就是“探求的过程”，是学习者通过思考获得意义和意向、在原有认知结构的基础上、形成新的认知结构的过程，是认知结构的完善与重新组织.数学问题解决指的是运用先前学得的知识和习得的经验按照一定的思维对策、在新情境下通过思考去实现学习目标的活动.

在数学解题过程中，问题解决者具有良好的数学认知结构，这是解题的基础.数学认知结构是个体将自己所认识的关于数学的信息组织起来的心理系统.认知结构，也叫做图式、架构、模型、组块、同化范例等.数学认知结构是数学知识结构在学习者头脑里的反映，它是学习者在学习的过程中逐步积累起来的在数学方面的观念系统.这些观念包括学习者通过学习一些数学概念和数学命题之后形成的表象信息和在解决问题过程中形成的数学具体方法，以及数学问题解决策略.

数学认知结构由数学知识、数学能力、数学思想等组成，如运算技能、作图技能、想象能力、推理能力等，这是解题的必要条件.一方面，问题解决需要学习者建立良好的数学认知结构，可以合理地把规则应用到适当的位置；另一方面，通过问题解决，学生的数学认知结构得到了调整与完善，使之更加合理、有效，再遇到该问题或类似问题时，调动记忆就能解决问题，问题解决后，通过归纳总结，学生的数学能力与数学素养将得到提高.

2 “多元二次变量的最值问题”课堂教学实践

2.1 问题与认知结构分析

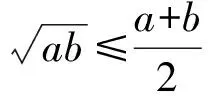
多元二次变量的最值问题，历来是学生学习数学和探究数学的难点.这类问题看似简单，似曾相识，然而思来想去，却很难求出正确答案.解决上述问题，不仅需要扎实的基础知识，而且需要丰富的解题经验，更需要良好的思维策略.围绕“多元”“二次”“最值”这3个关键词建立良好的认知结构(如图1)是成功解题的关键.

图1

2.2 例题解析与实战演练

例1若6x2+4y2+6xy=1，其中x,y∈R，则x2-y2的最大值为______.

分析已知条件是关于x,y的二次齐次方程，所求目标是x,y的平方差的最大值.

思路1根据重要不等式，通过合理配凑系数求解.

思路2将目标平方差转换为乘积，进行和差换元，令x+y=m，x-y=n，同时化归条件，转变为求mn的最大值.

思路3令x2-y2=t，通过“除一除”进行减元，化为“3个二次”问题，然后运用判别式求解.

思路4对条件配方，进行三角换元，转化为三角函数求最值.

解法1根据重要不等式a2+b2≥-2ab，合理配凑系数

1=6x2+4y2+6xy=6x2+4y2+2·x·3y≥

6x2+4y2-x2-9y2=5(x2-y2)，

得

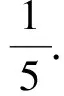
解法2根据不等式求最值原理，“和定，积求最大”，注意到所求目标为平方差.令x+y=m，x-y=n，则

x2-y2=mn，

可得

代入6x2+4y2+6xy=1，得

4m2+n2+mn=1，

从而

1=4m2+n2+mn≥5mn，

解法3观察目标与条件，发现它们都是关于x,y的二次齐次式，那么“除一除”就可以转化为“3个二次”问题.令x2-y2=t，则

当y=0时，可得

当y≠0时，可得

Δ=36t2-4(6t-1)(4t+1)≥0，

即

15t2+2t-1≤0，

解得

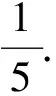
解法4多元问题可以考虑消元.对已知条件配方得

解得

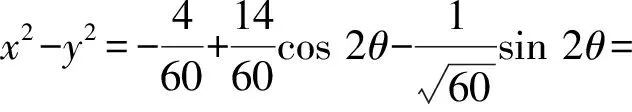
例2已知正实数a,b满足a2+b2-ab=3，则a+2b的最大值为______．

分析已知条件是关于a,b的二次齐次方程，目标是求二元一次式的最大值.

思路1将条件围绕目标作变形，运用基本不等式求解.

思路2对已知配方，将条件转化为平方和，进行三角代换.

思路3令a+2b=t，与已知条件联立方程组，消元转化为二次方程有实根，运用判别式求解.

解法1以目标a+2b为准，已知条件可化为

(a+2b)2-3b2-5ab=3，

即

(a+2b)2-3=b(5a+3b).

运用基本不等式可得

化简得

(a+2b)2≤28，

从而

解法2对条件等式配方，得

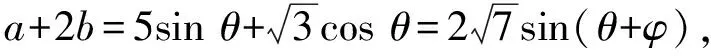
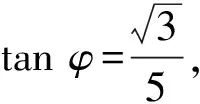
解法3令a+2b=t，则

a=t-2b，

代入a2+b2-ab=3，得7b2-5tb+t2-3=0,由

Δ=(-5t)2-28(t2-3)≥0，

例3已知实数a,b,c满足a2+b2+c2+ac+bc=1，则c的最大值为______.

分析已知条件是关于a,b,c的三元二次方程，目标是求c的最大值，思路是要想方设法将条件等式转化为含有目标的不等式，以实现求其最值.

解法1视a+b为整体，配方得

1=(a+b)2-2ab+c2+(a+b)c，

由重要不等式得

1=(a+b)2-2ab+c2+(a+b)c≥

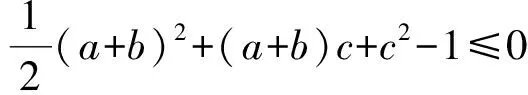
Δ=c2-2(c2-1)≥0,

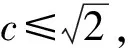
解法2对已知条件直接配方，得

从而

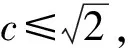
3 结束语

在学校教育中，要培养学生的数学核心素养，除了向学生传授基本的数学理论知识外，“解题”是最基本的教育方式之一.数学教育家波利亚曾指出：中学数学教学的首要任务就是加强解题训练，掌握数学就意味着善于解题.高三数学二轮复习教学活动一定要有所“变”，立足学情，以问题解决为导向，在解题过程中，启发学生将数学知识内容及其形态内化为认知的东西，纳入原有认知结构，新旧认知经过相互作用，新认知获得心理意义，从而使认知结构得到进一步的充实和完善.良好认知结构的建立，有助于打通“知识”与“能力”的“任督”二脉，使学生在掌握知识与技能的同时理解知识的本质，感悟知识所蕴含的数学基本思想，积累数学思想和实践的基本活动经验，并在此基础上促进学生形成和发展数学学科核心素养.