基于超声电机的新型舵系统研究

高炳东，张丛巨，曹东海，王红茹，熊官送

(北京自动化控制设备研究所，北京 100074)

0 引言

舵系统是飞行器系统的重要组成部分，其性能的好坏直接影响制导的优劣。随着未来智能作动系统和微型飞行器的精确制导对舵系统小质量、低噪声、快响应、无电磁干扰等方面提出越来越高的要求，而现使用的电磁电机小功率舵系统存在启动制动慢、频繁启动制动换向时电流波动大、直驱力矩小等不足，越来越无法满足其需求。

随着近年对材料特性[1-3]、材料工艺[4-5]、运动机理[6-7]及机械结构[8]等方面的研究逐步完善，超声电机本体性能日益凸显，在国外航天领域已得到较广泛的应用。

自20世纪末开始，美国喷气推进实验室 (Jet Propulsion Laboratory，JPL)将超声电机用于多功能爬行系统，该系统用于航天飞船外舱壁的检查，其承载质量与自重比达10∶1，充分发挥了超声电机高转矩密度的特点；利用其低速大力矩的特点，美国国家航空航天局(National Aeronautics and Space Administration，NASA)在卫星探测器的轻量机械臂上采用超声电机取代有刷直流电机[9]，改进后Mars Arm II的结构虽与Mars Arm I相似，但质量减小了40%，其主要原因是超声电机直接驱动，无需减速装置；利用其高精度的特点，法国Cedrat公司开发出一种堆叠式压电陶瓷的直线超声电机，在6V交流电压驱动下可输出45N的推力，在直流工作模式下，其位移分辨率可小于1nm，已应用于太阳神法国军事侦察卫星的Helios望远镜的倾角调整机构上；利用其驱动方式灵活的特点，日本宇宙科学研究所研制了两种直线超声电机用于空间伸展结构的伸展和收缩；利用其响应快的特点，美国和法国将其用于导弹的测控系统；利用其结构简单可微型化的特点，日本研制了微型超声电机用于微卫星等领域。

另外，NASA和美国国防高级研究计划局(Defense Advanced Research Projects Agency，DARPA)正在进行无尾智能机翼研发，其目的是将智能材料技术应用到军用飞行器上，以减小结构质量，提高军用飞行器的空气动力和气动弹性性能[10]。该项目第二阶段的重要目标是运用高带宽智能作动器，实现无铰链、可变形的翼展和翼旋方向的高效快速驱动。为此对形状记忆合金(Shape Memory Alloys，SMA)、电活性聚合物、液压泵、电磁电机及超声电机为基础的设计方案进行比较表明：应用超声电机作动器的方案效果最好，超声电机转矩密度高于当前任何智能材料作动器或者电机；更为重要的是，由于超声电机的结构紧凑、灵活，可以使其在30%的风洞模型的有限空间中与其他部件进行有效集成，大大减小了机翼质量。由于具备结构灵活轻便和响应迅速等特性，在飞行高度为20～100km的高空，且随气流变化需要改变机翼和机身现状的智能飞机和扑翼式仿生飞行器中，超声电机具有极强的优势[11]。

由此可见，超声电机以其小质量、低噪声、快响应、无电磁干扰、断电自锁等特点，将在航天航空等领域中受到愈来愈大的重视。

本文针对旋转型两相行波超声电机，开展了驱动控制技术研究，完成了一种相比电磁电机小功率舵系统更具有高精度和快响应等特点的超声电机舵系统原理样机的研制，为下一代智能作动系统和微型飞行器发展提供了技术支撑。

1 超声电机运行机理及特性分析

超声电机是一种利用压电材料的逆压电效应来驱动的新原理电机，主要由定子和转子组成，如图1所示。定子由经极化处理的压电陶瓷片和表面带梳状齿的环状金属弹性体黏结成一体，而转子上黏结一层摩擦片，通过弹性体压缩变形产生的轴向压力来增大定和转子之间的摩擦驱动力。其驱动机理为：压电陶瓷片在两相交变电压的作用下激发模态响应，产生超声波振动，黏结在压电陶瓷片的弹性体梳状齿由此产生椭圆运动，通过摩擦作用带动转子运动。

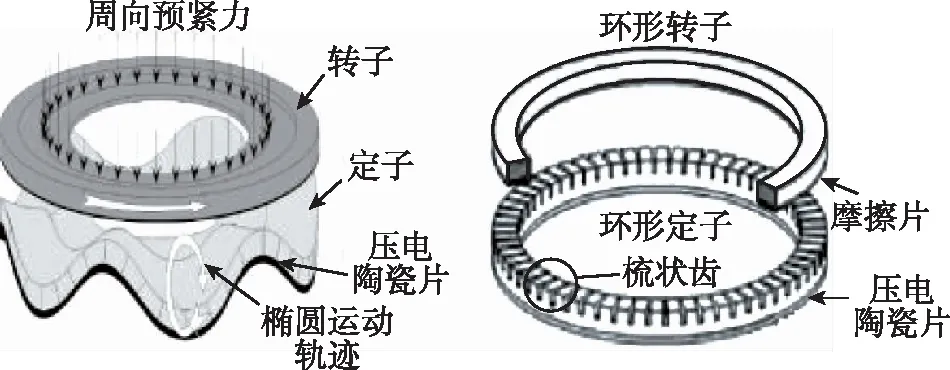
图1 超声电机结构图Fig.1 Structure diagram of ultrasonic motors

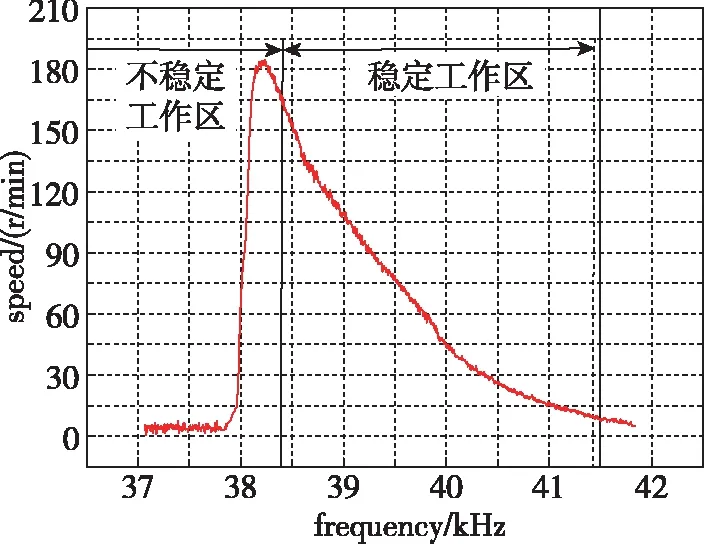
图2 USM-60频率-转速特性曲线Fig.2 Curves of USM-60 frequency-speed characteristic

由超声电机的工作原理可知，当在压电陶瓷片上所施加的驱动电压频率接近电机谐振频率，且信号具有一定的功率时，定子就能激发出电机相应的工作模态，从而使电机运转起来[12]。但当驱动频率远离谐振频率时，容易激发出非工作模态，极不利于电机控速[13]。本文选用的超声电机USM-60在工作模态下的转速特性测试结果如图2所示，当驱动电压频率接近谐振频率时，转速达到最大值182r/min，但由于定子振幅急剧放大，极可能超过压电陶瓷片所能承受的极限，导致压电陶瓷换能片断裂，对电机造成永久性损坏。因此，在调频调速模式下，USM-60驱动电压频率范围为38.5～41.5kHz，在该范围内，频率越高，定子振幅越小，电机转速越低；反之，频率越低，定子振幅越大，电机转速越高。

2 超声电机舵系统构架搭建

基于超声电机的新型舵系统设计框图如图3所示，主要由机械结构单元、控制单元、驱动单元、反馈单元和匹配电路单元组成。

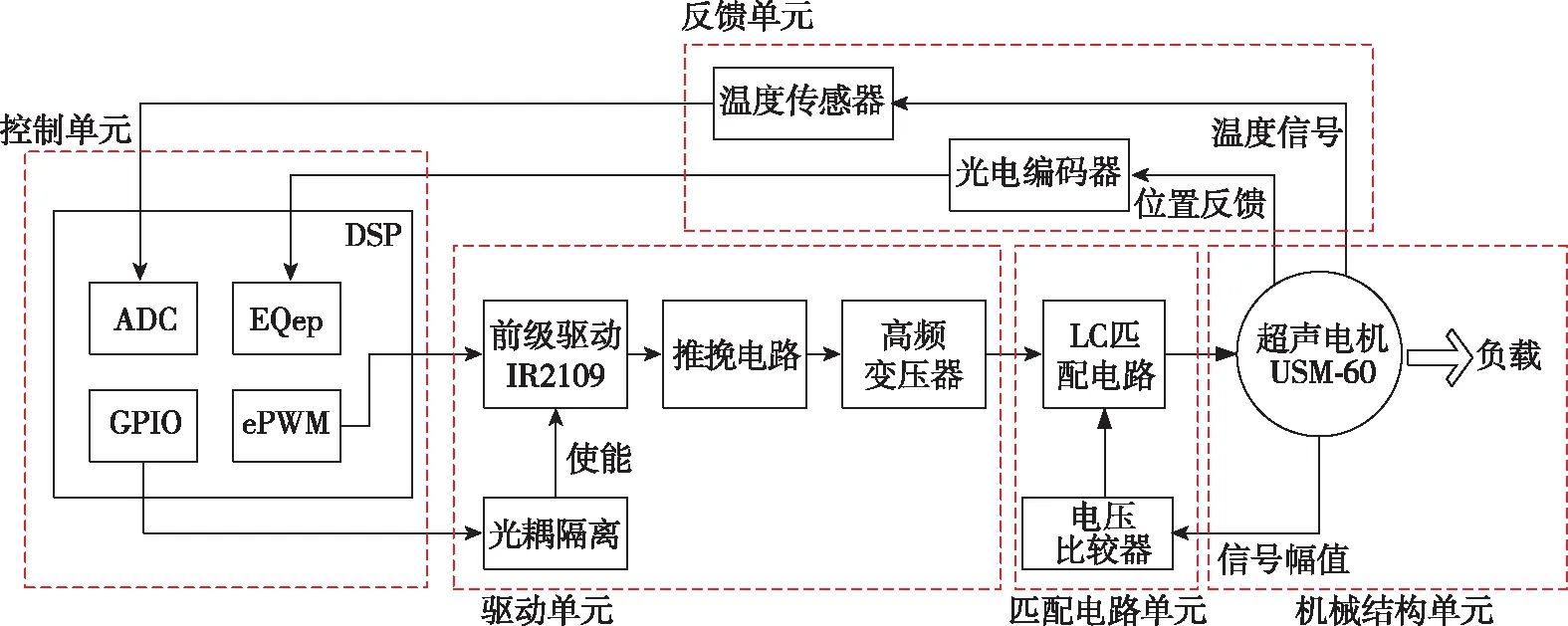
图3 超声电机舵系统框图Fig.3 System block diagram of the rudder system based on ultrasonic motors

2.1 机械结构单元

选用的超声电机USM-60具有低速大力矩的特点，在频率为39kHz的驱动电压作用下，额定转速为117r/min，额定力矩为1.0N·m ，满足某小型导弹工程应用需求，因而系统无需经减速机构，电机直接驱动负载。

2.2 控制单元

控制单元是系统的核心，通过数据通信获取目标指令，并对位置和温度等反馈信号进行获取和解算，基于控制算法周期性地改变输出控制信号频率，达到控制电机的目的。微处理器采用数字信号处理器(Digital Signal Processor，DSP)，其中包括eQEP、ADC、ePWM、GPIO等模块。将超声电机上的光电编码器接至eQEP，DSP接收光电编码器的脉冲数，通过计算把它转化为位置信息；ADC模块将温度传感器输出的电压模拟信号转化为数字信号，解算后获取电机温度；系统设置GPIO引脚的高低电平作为控制前级驱动的使能信号，控制系统信号的输出，从而控制电机的启停；通过ePWM产生不同频率的控制信号。

2.3 驱动单元

驱动超声电机需要一定功率的高频高幅值的驱动电压。因而，由DSP产生的信号需要经过功率放大电路进行放大，从而实现电机的驱动。本文驱动单元由前级驱动、推挽电路和高频变压器组成，如图4所示。

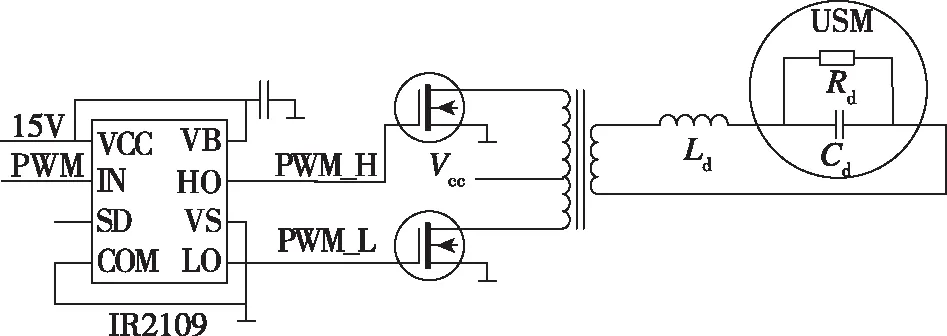
图4 驱动单元(单路)Fig.4 Driving units (single channel)

前级驱动芯片IR2109将脉冲宽度调制(Pulse Width Modulation，PWM)信号升压至15V，高端和低端分别输出互补的PWMA_H 和PWMA_L 。

由于推挽电路结构相对简单，输出功率较大，输出纹波电压较小，适宜在超声电机这种输入电源电压低且输出功率也不大的情况下应用。推挽电路将PWMA_H和PWMA_L作为输入，功率开关Q1和Q2交替导通，栅极的电压方波在开关管的漏极上产生相应的电压方波，由高频变压器再次放大后驱动电机。

2.4 反馈单元

高精度的位置反馈信号对于闭环控制系统十分重要，直接影响控制策略的好坏与被控对象的控制精度。本文选用Autonics的E40H系列增量式光电编码器，分辨率为5000线，DSP中的位置计数器QPOSCNT对编码器输出QEPA和QEPB的上升沿和下降沿进行计数，即1圈计数20000次。因此，实际角度φ与QPOSCNT的关系为

(1)

另外，超声电机的谐振频率对温度十分敏感[24-25]，采集温度信号并对其进行温度补偿的算法必不可少。本文由恒流源输出5mA的恒定电流通过贴在压电陶瓷片上的热敏电阻，热敏电阻上的电压由DSP片上ADC进行模数转换后即能解算出温度信息。

2.5 匹配电路单元

当驱动信号为正弦波时，电机的机械振动特性最佳[14]，另外超声电机呈强容性特征。为了实现能源的高效转换，避免激发出高频谐波成分，往往需要在驱动电源和电机之间加上匹配谐振电路，将方波信号转化为正弦信号，同时进行电压增益。然而，现广泛应用的LC谐振[15]和LCC谐振[16-17]等超声电机匹配电路方案的谐振电压增益易受驱动电压频率或温度影响，导致输出电压幅值发生变化，从而造成调频调速方式下电机转速控制变量驱动电压频率和幅值发生耦合的问题，大大提高了超声电机转速控制的难度。

为此，本文提出了一种带反馈回路的LC谐振电路，如图5所示。通过对输出Vout进行采样，不断调节中间变量Vcc，从而使输出驱动电压幅值Vout保持恒定，不受温度和驱动电压频率的影响。

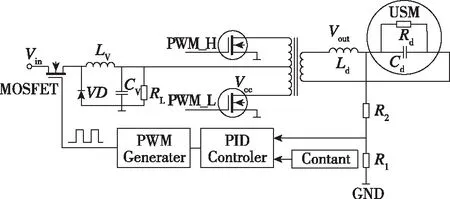
图5 带反馈回路的LC谐振电路Fig.5 LC resonant inverter with feedback loop

通过实验验证，表明：当系统中的LC谐振电压增益为1.7时达到稳态，Vcc=(8.82±0.015)V，Vout=(374.7±0.06)V，稳态误差为0.3V；当LC谐振电路受到驱动电压频率或温度影响，电压增益由1.7突变至2.3时，Vout同时骤升至507.6V，为此Vcc不断跌落，以使Vout降至目标值；经过6.18ms后系统达到稳态，Vcc=(6.528±0.009)V，Vout=(375.4±0.06)V，稳态误差为0.4V。

可见，设计的带反馈回路的LC谐振电路输出电压幅值基本保持恒定，不受温度和驱动电压频率的影响，且调节速度快、精度较高，实现了超声电机转速控制变量解耦，显著降低了超声电机的控制难度，对超声电机的推广与应用具有重要的意义。

3 超声电机舵系统运动控制策略

目前，针对超声电机的神经网络控制[18]、模糊控制[19]、模型参考自适应控制[20]、鲁棒控制[21]、滑模变结构控制[22-23]等算法已有所研究，使超声电机的控制性能得到改善。但是由于目前尚无准确的数学模型，且控制算法的复杂度高，导致系统硬件和软件可靠性降低，离应用于高可靠性工业场合仍存在一定差距。

与传统电磁电机不同，超声电机具有启动停止响应极快、断电自锁、惯量小等特性，Bang-Bang控制的应用极有助于加快系统控制过程，具有显著的优势。

本文在超声电机Bang-Bang控制律的基础上，提出了一种超声电机简化Bang-Bang控制策略，充分发挥了超声电机的极佳响应特性，显著降低了超声电机的控制难度。

3.1 Bang-Bang控制算法求解

利用Matlab系统辨识工具箱对超声电机驱动电压频率-位置开环系统进行系统参数辨识。为方便算法推导，选用双积分系统模型，拟合度R2为92.35%，状态空间方程为

(2)

式中，x1为状态量1，表转速；x2为状态量2，表位置。

求解得转移到状态空间原点的两段相轨迹γ+和γ-，则开关曲线γ(图6)方程为

γ=γ+∪γ-={(x1,x2)x2=-0.051x1x1}

(3)

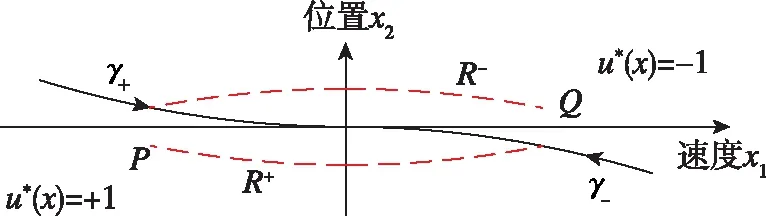
图6 相平面上的开关曲线及划分区域Fig.6 Switching curve and zones in the phase-plane

其中箭头方向为状态转移方向，开关曲线γ将相平面分割成R+和R-这2个区域，可以表示为

(4)

不论初始状态位于R+还是R-，在实现状态向坐标原点转移时，都必须经过开关曲线γ改变控制的符号，产生控制切换。另外，初始状态(x10,x20)唯一地确定了当前应采用的最优控制。超声电机Bang-Bang控制律为

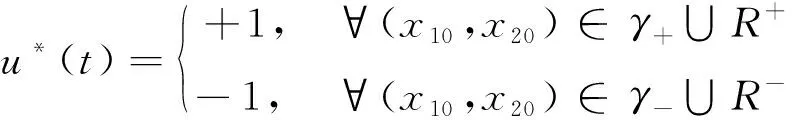
(5)

3.2 简化Bang-Bang控制算法

由图6可知，超声电机开关曲线极其扁平，随转速x2的减小，位置x1变化较小，其物理意义为电机停止响应时间很小，正如实验测量，其值仅大约为0.36ms。

另外，在实际舵系统位置伺服的情况下，其最终目标集为位置x1= 0的一个δ邻域内即可，其中δ为舵系统容许误差。

因此，将R+和R-这2个区域简化为位置x1<-δ和位置x1>+δ。系统根据目标位置指令以正最大控制变量或负最大控制变量运转，持续观测位置x1，在容许误差带内利用超声电机断电自锁和惯量小的特性进行快速停止。简化Bang-Bang控制律为

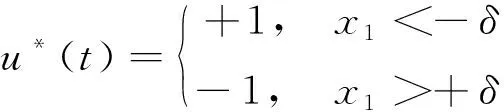
(6)

对应控制切换示意图见图7。

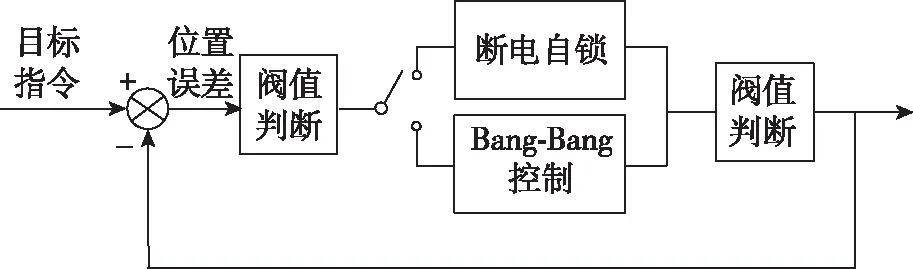
图7 控制策略切换示意图Fig.7 Control strategy switching diagram

仿真实验表明：超声电机在PID控制下频带为45Hz；在Bang-Bang控制下，偶有回调现象，导致定位失败；在提出的简化Bang-Bang控制下，频带达到73Hz 。因此，简化Bang-Bang控制的应用加快了系统控制过程，具有显著的优势。

4 实验验证

在前文系统构架搭建和运动控制策略研究的基础上，完成了基于超声电机的新型舵系统原理样机的研制，如图8所示。由于系统额定力矩为1N·m，限位定义为 ± 20°，因此选定模拟外界负载的弹性扭杆扭矩为0.05(N·m)/(°)(图中未标出)。

图8 超声电机舵系统原理样机Fig.8 Principle prototype of the rudder systembased on ultrasonic motors

舵系统使物体的位置输出变量能够跟随指令，其最重要的指标为稳态误差和频带，分别反映位置精度和动态性能。因此，下面分别对该系统的精度和动态性能进行测试和分析。

4.1 舵系统精度性能实验

通过测试软件对负载情况下的超声电机舵系统稳态精度进行测试，其中指令更新周期为15kHz，系统控制周期为15kHz，位置采样周期为375Hz，测试位置指令分别为5°、10°、15°和20°。

如图9所示，在0.05(N·m)/(°)的弹性扭杆负载下，超声电机舵系统在5°、10°、15°和20°等位置指令下阶跃响应过渡过程平均转速为280～320(°)/s ，超调量小于3%， 稳态精度分别为0.018°、0.018°、0.036°和0.09°。

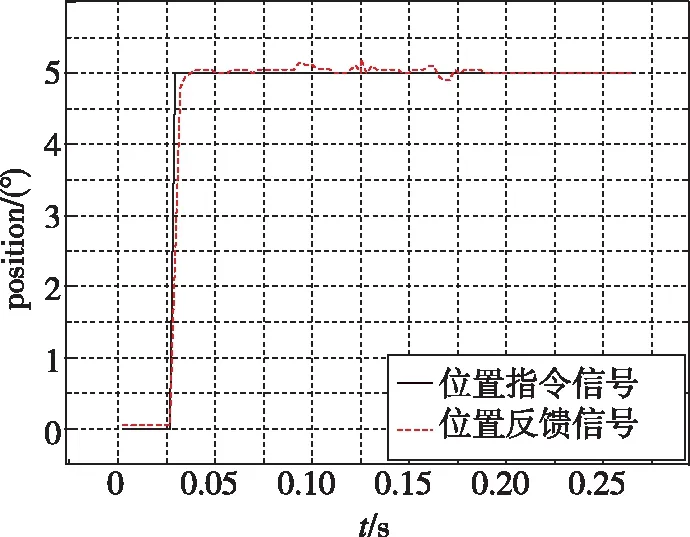
(a)5°指令阶跃响应曲线

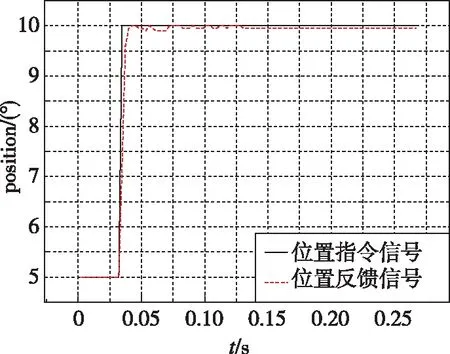
(b)10°指令阶跃响应曲线

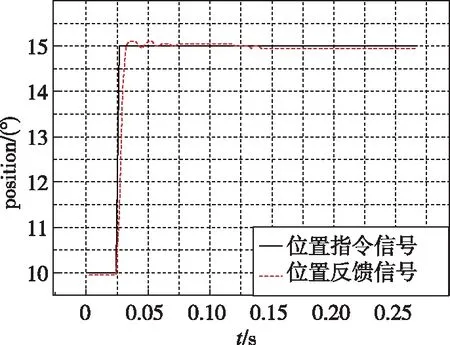
(c)15°指令阶跃响应曲线

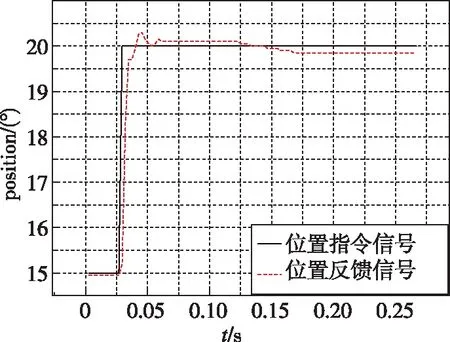
(d)20°指令阶跃响应曲线图9 超声电机舵系统位置精度测试结果Fig.9 Position accuracy test results of the rudder system based on ultrasonic motors

4.2 舵系统动态性能能测试

通过测试软件对负载情况下的超声电机舵系统动态性能进行测试，其中指令更新周期为15kHz，系统控制周期为15kHz，位置采样周期为15kHz，测试位置指令为频率逐渐升高的正弦信号。

如图10所示，在0.05(N·m) /(°)的弹性扭杆负载情况下，超声电机舵系统在70Hz正弦信号时，位置反馈信号波形未衰减至-3dB；在80Hz时，衰减至-3dB以下，相位滞后均未达到90°。因此，在空载情况下，系统响应频带为70～80Hz 。

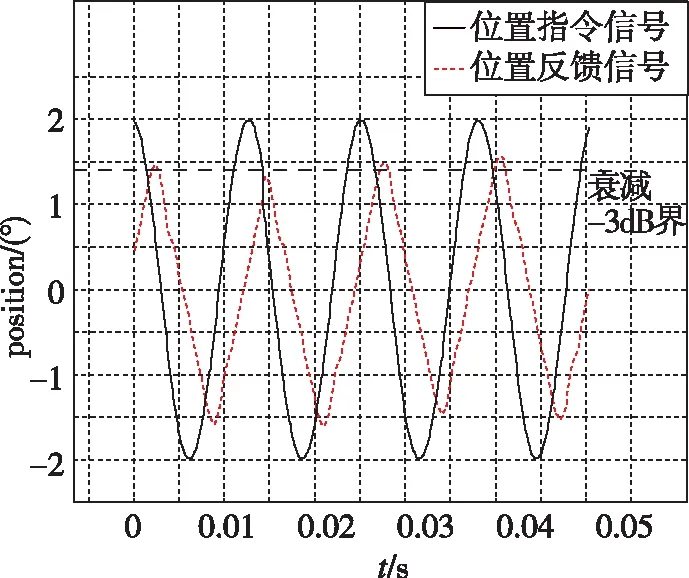
(a)70Hz正弦指令响应曲线

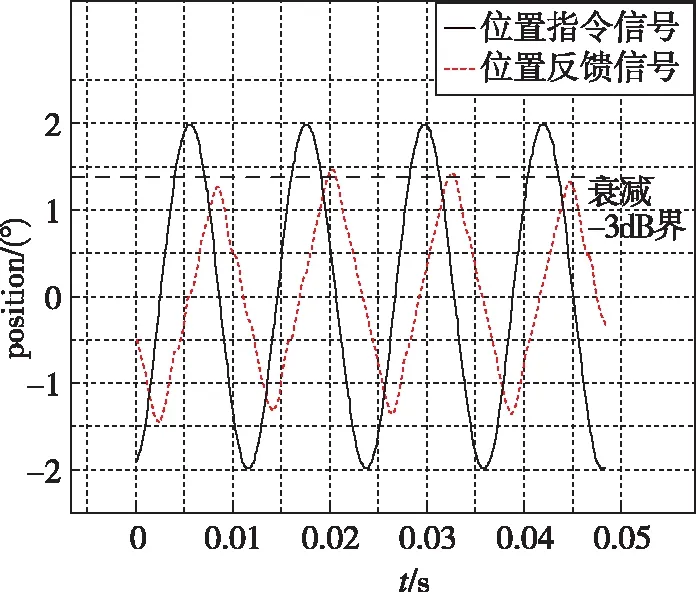
(b)80Hz正弦指令响应曲线图10 超声电机舵系统动态性能测试结果Fig.10 Dynamic behavior test results of the rudder system based on ultrasonic motors

4.3 实验结果分析

通过以上对超声电机舵系统负载情况下的精度和动态性能测试数据表明：该舵系统位置稳态误差小于(0.018 °+δ×4‰)(δ为指令角度)，频带达到70Hz以上；而传统电磁舵系统的稳态误差一般在(0.15°+δ×1%)左右，频带很难达到30Hz以上，对比足见超声电机位置舵系统的精度和快速性极佳。

5 结束语

超声电机由于其小质量、低噪声、快响应、无电磁干扰、断电自锁等特点，满足航天领域未来的发展需求，并且超声电机在国内尚未得到成熟应用。本文针对小型无人机、微型导弹等小功率精确制导武器执行机构领域，开展了超声电机驱动控制技术研究，提出了一种简化Bang-Bang控制策略，最终实现了稳态误差小于(0.018 °+δ×4‰)，频带大于70Hz的超声电机舵系统样机的研制。