基于多目标算法的空中作战任务规划框架研究

郭昱普，蔡 飞，潘志强

(国防科技大学信息系统工程重点实验室，长沙 410073)

0 引言

空中作战任务规划是一个很复杂的过程，首先要通过联合作战空中评估流程将指挥员的意图转化为联合空中作战计划，联合指挥中心的计划人员必须通过准确分析战场空间信息来提高态势感知能力[1]。制订作战计划时，决策人员根据所需要执行的任务清单来制订合理的联合空中作战计划，飞行员负责听从指令完成任务[2]。空中作战任务规划给规划任务带来了非常大的挑战，其主要难度体现在以下几个方面：

首先，空中作战是一个动态的过程[3]，战场态势变化迅速，这就是一个很强的时间限制。以观察-判断-决策-行动(Observation-Orientation-Decision-Action, OODA)环为例，完成从侦察到打击的过程本身就需要很长的时间，其中留给规划决策的时间更是紧迫。

其次，随着敌我飞行器数量种类的增加，需要执行的任务规模也随之扩大，将大批量的任务分配给大批量的飞行器会导致组合爆炸。因此即便是拥有较长的规划周期，对于实现全局最优规划也是十分棘手的[4]。

第三，有效的任务规划服从某些强制性的约束。在空间上，可能表现为打击目标不能突破某些禁飞区；在时间上，我方飞行器可能无法在特定的时间窗口到达打击区域；在其他飞行器能力方面，如燃料、携带弹药、速度等，都可能成为限制任务完成的潜在因素，所以可行域是不连续的。因此，大部分基于梯度的搜索方法能力明显不足。

第四，目标函数的设置不确定性强。在打击目标的任务中，更看重对目标最大限度毁伤的可能性；在情报侦察监视的任务中，更看重最大限度地覆盖目标区域。鱼和熊掌不能兼得，不同的优化目的可能本身是相互冲突的，例如，如果追求毁伤目标的最大可能性，可能意味着我方战机需要较长的追击距离，这就增加了我方战机自身被摧毁的可能性。

有限的决策时间、庞大的任务规模、复杂的可行域以及相互间存在矛盾的目的函数给空中任务规划带来了巨大的压力。空中作战任务规划可以看作多目标优化问题，其特点是规模大、存在多个相互冲突的目标。进化算法被广泛应用于寻找多目标优化问题的最优解，在设计全局搜索方法时，多样化和集约化是2个主要的问题。多样化是指在搜索空间中访问多个不同区域的能力，而集约化是指在这些区域内获得高质量解决方案的能力。本文在算法层面提出了一种多目标进化算法，也从顶层设计了空中作战任务规划框架，并且给出了2个具体决策的例子。

1 空中作战任务规划框架

在信息战条件下，为了解决空中作战任务规划的问题，仅通过规划者和指挥人员的辛苦工作是远远不够的。本文提出了空中作战任务规划的工作流程框架,需要借助许多辅助决策的信息工具:例如将实际问题转化成数学模型的数学建模工具,用于解决多目标优化问题的进化算法的程序和软件以用于评估方案，预测可能导致的情况的作战仿真的工具等。本节提出的规划架构如图1所示。

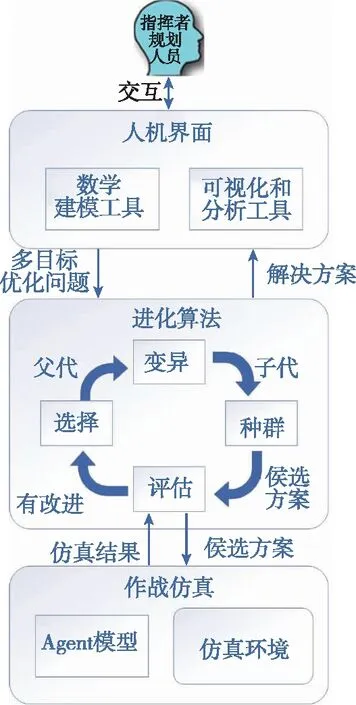
图1 空中作战任务规划框架Fig.1 Frame of air combat mission planning

在给出的空中任务规划框架中，通过作战仿真的方式对方案进行评估。为了迅速完成规划，采用低保真的作战模拟环境。

文中采用的是一种基于agent的仿真方法，每一个作战单元都可以看作是一个动态的agent，将agent看作是一个智能体，每个agent有自己的运行规则，甚至可以有自己的博弈策略。近年来，随着计算机计算能力的提高，基于agent的仿真方法得到了更加广泛的接受。此外，与经典的战争数学模型(如兰彻斯特方程)[5]相比，它具有能够直接对系统中实体进行建模的显著优势。这允许从不同实体的低级交互中产生系统级的影响，在对较为复杂的情况进行建模时，这可能是有利的[6-8]。

2 多目标进化算法概述

多目标进化算法是一种广泛被应用在优化问题上的智能算法。进化算法的提出受到了达尔文进化论的启发。在解决优化问题时先随机地构建一些初始解，然后通过评价保留一些解、淘汰一些解，被保留的解通过进化随机产生后代解，然后再进行评估。通过不断迭代，相当对可行域进行了一个优胜劣汰的选择，迭代的次数越多，获得帕累托最优解的概率就越大。由于多目标优化问题在大多数情况下的梯度是不连续的，所以进化算法的表现要明显优于基于梯度的算法。

搜索算法必须在有冲突的2个目标之间取得平衡。混合启发式算法的设计具有控制这种平衡的能力[9]。本文提出的搜索自适应多目标进化算法将工作扩展到连续搜索领域，开发了一种混合进化算法，并且在多目标进化算法的框架下集成了一组自适应的搜索策略。本算法从不同搜索操作的协作和一体化中取得了良好的效果，同时，还能够根据现有问题选择合适的搜索策略。

2.1 基本概念和定义

如果没有一般性约束，多目标优化问题可以写作

MinimizeF(x)=(f1(x),f2(x),…,fm(x))
Subject to:x∈Ω

这里，F(x)是一个m维的目标向量，fi(x)是第i个优化的目标，x=(x1,…,xn)T是n维的决策变量，Ω是可行决策空间。

定义1：一个可行解是x优于另一个可行解y(定义为xy)，使得fi(x)≤fi(y)，∀i∈{1,…,m}。

定义2：一个解是帕累托最优的充分条件是不存在y使得xy。

定义3：帕累托最优集(P*)是所有帕累托最优解的集合

P*={x∈Ω|∀y∈Ω,y≻x}

定义4：帕累托前沿(Pareto Front, PF)是帕累托最优集在目标空间的映射

PF={F(x)=(f1(x),…,fm(x)):x∈P*}

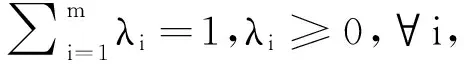
2.2 遗传操作

交叉和突变是最有名的2个遗传操作。交叉是交换父母的遗传物质以产生新的后代的过程。而突变算子则用于保持种群在世代间的多样性。下面主要介绍了模拟二进制交叉(Simulated Binary Crossover, SBX)、多亲本交叉和多项式突变。

SBX在实际应用中得到了广泛的应用。它在许多具有连续搜索空间的测试问题中都能很好地工作。对于一对父母节点xa和xb，SBX产生一个后代y如下

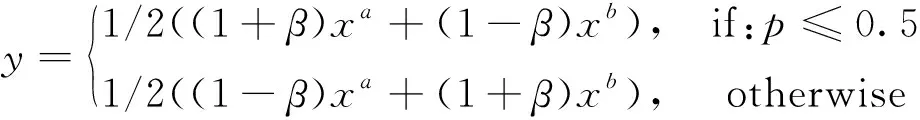
这里，p,u∈[0,1]是2个随机数，ηc是分配指数。

目前在连续搜索领域提出了多种多父交叉，例如单纯形交叉(Simplex Crossover, SPX)和父中心交叉(Parent-Centric Crossover, PCX)等。然而，本文中提出的算法使用了新多父交叉(Multi-Parent Crossover, MPC)。MPC从3个不同随机选择的父母中交叉构建了一个新的子女，公式如下

这里，β～N(μ,σ)是满足高斯分布的随机数，p∈[0,1]是均匀分布的随机数。

在多项式变异中，在靠近父结点的地方生出一个子结点的概率大于在远离父结点的地方生出一个子结点的概率。突变体后代

这里，uj∈[0,1]是满足均匀分布的随机数，分布指数ηm和突变指数pm是2个控制参数。aj和bj是xj的上限和下限。

2.3 差分进化算法

微分进化算法是一种简单有效的搜索算子，主要用于求解连续域的优化问题。微分进化的成功依赖于微分突变，利用搜索域内的候选解来构建差分向量。每个差异向量被缩放并添加到另一个候选解中，生成所谓的突变向量;然后，微分进化将突变向量与父代解重新结合，生成新的子代;当子代具有同等或者更好的适应度时，才能取代父代。差分进化有一些控制参数如缩放因子F，用来缩放差分向量，以及交叉速率CR。给定N个个体的总体P，为每个目标个体随机选择3个不同的个体xa、xb、xc，目标个体xi∈P,∀P∈{1,…，N}。突变体vi由下述公式生成。然后，将二项交叉应用于vi和vi，生成新的子代。

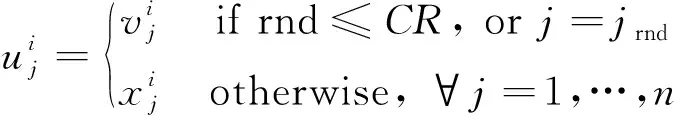
其中，rnd∈[0,1],jrnd∈{1,…，n}是一个随机选择的索引来确保至少有一个组件ui是由vi所提供，n是个体的长度，CR∈[0,1]。

3 基于搜索自适应的多目标优化算法

3.1 算法表述

根据第2节的基本概念，把空中任务规划多目标优化问题转化成以下数学表达式

miny=F(x)=(f1(x),f2(x),…,fk(x))

e(x)=(e1(x),e2(x),…,em(x))≤0,

x=(x1,x2,…,xn)∈X

X={(x1,x2,…,xn)|li≤xi≤ui,i=1,2,…,n}
L=(l1,l2,…,ln)
u=(u1,u2,…,un),y=(y1,y2,…,yk)∈Y

其中，x是决策变量，y是目标变量，X是决策变量空间，Y是目标函数变量空间，L和u分别是决策变量空间的下界和上界，e(x)是约束函数向量。把群体中的个体看作是相空间中的粒子，首先选出初始的一代，然后通过计算熵和自由能确定候选的父粒子，最后通过差分算法给出遗传变异规则确定的后代。给出的算法过程如下：

步骤1：设置t=0，然后随机生成初始种群P0={x1(t),x2(t),…,xN(t)}。

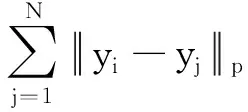
xi(t))-fj(t-1,xi(t-1))))(自由能的表达式)，然后利用下面的比较规则计算第i个粒子的秩函数值

if ((xiπxj)∨(xiπ=xj)∨(xi⟺xj∧si>

sj)∨(xi⟺xj∧si=sj∧pi(t,f(t)))<=

pj(t,f(t)))∨(xi～xj))

then Rank(xi(t))=Rank(xi(t))+1;

else Rank(xi(t))=Rank(xi(t))

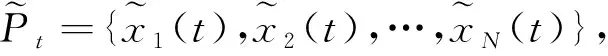
步骤4：将新生成的l个粒子添加到种群Pt中从而形成新的种群Pt′。

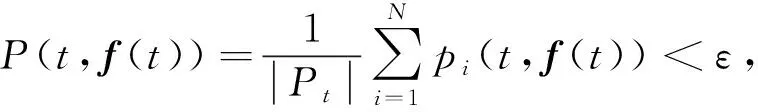
3.2 实验结果

实验中，为了验证该算法的计算性能，对四种典型的基准函数(ZDT1～ZDT4)[10]进行了测试。ZDT是一套测试优化算法的基准函数集，测试了该算法在不同情况下解决复杂的多目标优化问题的能力。结果如图2所示。

从图2可以看到,通过使用这种新算法不仅可以求解凸最优帕累托(ZDT1)和凹最优帕累托前沿(ZDT2),而且还可以求出离散最优帕累托前沿(ZDT3)；同时，该算法收敛速度(ZDT4)更快,性能优于传统的多目标进化算法。

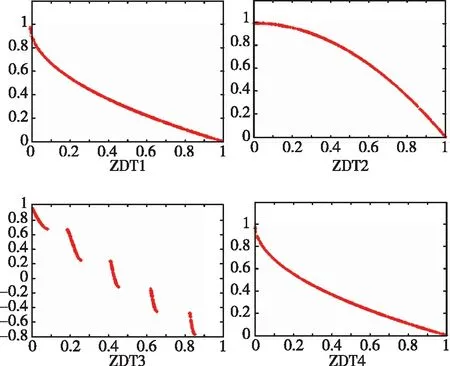
图2 实验结果图Fig.2 Experimental results diagram

4 规划框架的具体应用

使用文中所提出的空中任务规划框架，做了几个具体场景下的应用，设计了几个决策支持的工具。第一个解决了空中动态目标的打击问题，随后将该框架扩展到情报侦察领域，并且尝试着将其推广到无人机任务规划领域。

4.1 动态目标打击任务

动态目标打击任务是指敌方飞行器突然在我方领空出现时，我方利用一切可以利用的装备资源尽最大可能将其毁伤。动态目标打击小组的规划人员必须快速生成并评估具有特定约束条件的打击备选方案，需要考虑的问题有以下几点[11]：

1)我方可以使用哪些装备对目标进行打击；

2)哪些武器装备可以在时间窗口内到达打击地域；

3)战机携带哪些弹药可以成功地实现对目标的打击；

4)方案会达到什么样的效果，以及如何处理级联效应。

这个过程往往发生在战机正在空中执行日常巡航任务的过程中，所以必须在几分钟之内做出决策。因此，使用自动化辅助决策系统可以极大地提高效率。

在打击动态目标的任务中，任务规划人员会根据上级的决心先确定行动希望达到的目的。所给框架中的目的子集包括：1)最大限度地提高敌方目标被毁伤的概率；2)最大限度地降低我方装备被威胁的概率；3)最小化我方装备被毁伤的概率；4)尽量使高优先级的目标被毁伤得最多。

由求解多目标优化问题得出的方案中包括负责执行任务的我方战机以及其针对的目标。每次筛选要先根据限制条件确定可行解集，例如，一个已经消耗完弹药的我方战机不能再执行打击另外一个目标的任务；在机会窗口结束之前无法到达的我方战机不能被分配任务。其动态任务表示如图3所示。

图3 动态任务规划表示Fig.3 Dynamic targeting mission plan genetic representation

通过这种直接的两点交叉的编码方式，采用均匀变异的标准遗传算子来动态地更新可行解集。有时可行解是将一个任务同时分配给2个装备，可能会在实际情况中产生冲突或矛盾。

该方法给动态目标规划领域提供了一个可行的方案，这样的方式同样可以应用到武器规划部门，用于分析武器装备开发过程中潜在新兴目标的影响。这个动态分配任务的框架被用于支持建模和基于模拟的实验。

4.2 情报侦察任务规划

目标打击任务是空中行动的重要环节，但是不能孤立的运作。指挥中心下设的情报侦察部门负责向决策者提供准确、相关和及时的情报，在此基础上形成情报预测能力和态势感知能力。与打击任务相似，情报侦察部门也需要规划人员制定侦察巡航计划，利用我方装备所携带的传感器和侦察平台，对目标区域进行侦察探测以满足情报需求。在情报侦察领域，同样可以使用空中作战任务规划框架。

目标打击任务是在尽可能保全自身的同时追求最大限度地杀伤敌人，在情报侦察领域目的产生了新的变化，目的子集包括：1)最小化每一个装备所走的总距离；2)最大化对时间窗口要求的服从；3)最大化覆盖尽可能广的地理范围。

任务计划包括将可用的侦察装备分配给可观察站点的有序集合，每个可用装备都配有一组传感器，保证其能够收集信息。每个可观察站点都有一组与情报收集类型相匹配的相关情报需求。

最初表示收集计划的方法是采用多层遗传表示。在这种表示方法中，个体由一个或多个装备路由基因组成，其中每个装备路由基因包含一组装备探测的路径点。图4展示了其中一个示例，小写字母是观察站点的标识符；D表示仓库，是装备的初始位置，仓库可以用作模拟加油，并且具有产生多条路线的附加效果；N是一个无操作指示符，用于模拟可变长度的遗传表示。

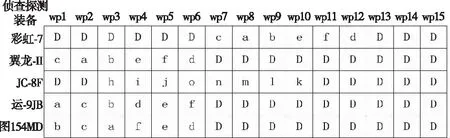
图4 侦察探测任务计划遗传表示Fig.4 ISR mission plan genetic representation

遗传变异算子在个体水平和基因水平上都起作用(如图5)交叉操作采用单点交叉，从一个亲本中选取一个完整的装备路径基因子集，并与另一个亲本互补的基因结合。在基因层面，每个侦察探测装备在2个候选计划之间执行额外的单点交叉，交换部分装备路由的各个部分，然后执行均匀突变，选择一个可行的收集点并替换当前路径点。

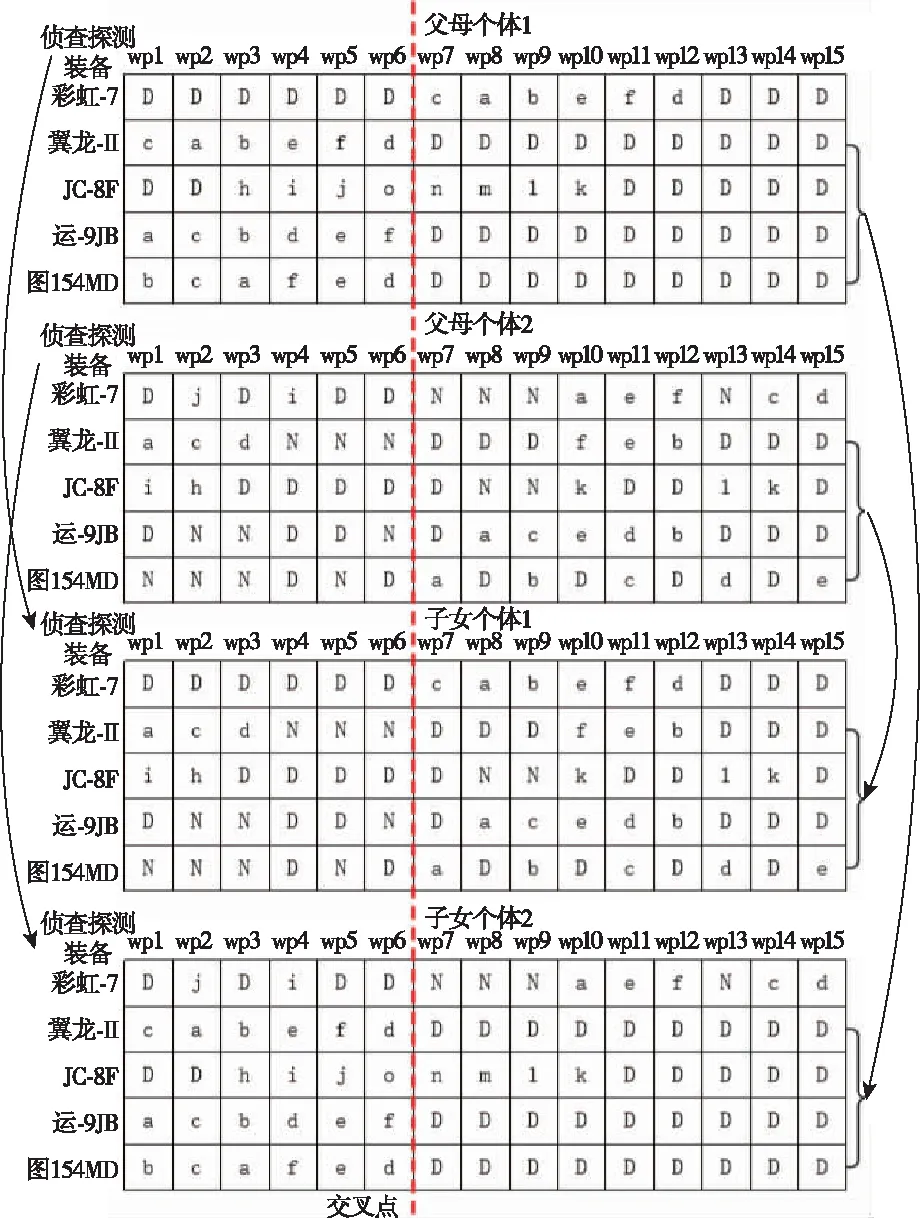
图5 侦察探测任务计划多层次遗传变异Fig.5 ISR mission plan multi-tiered genetic variation

在使用这种遗传表示的实验中，该方案其实是对合作共同进化算法的一种近似[14]。在合作共同进化算法中，每个种群都包含代表更大解决方案的一个组件的个体。这些种群的进化是并行进行的，相互作用只是为了获得适应性。

该改进的算法是为每个可用的侦察探测装备形成一个子填充，其中的个体构成该资产的个体收集计划，然后通过从每个子填充中选择单个成员形成一个完整的收集计划。交叉和变异是在种群水平上进行的，是一个标准的进化算法。为了进行评估，群体中的一个成员与上一代最优秀的成员相互协作，形成一个完整的候选解决方案。

5 结论

通过以上理论分析和实验分析得出结论，构造的新的多目标进化算法明显提高了传统多目标任务规划的性能。原因是这种新算法结合了自由能最小化和粒子系统的熵增加定律相空间,然后驱动所有粒子参与交叉和变异的所有时间,以便快速准确地获得帕累托解。

空中任务规划是一个非常复杂的过程，随着武器装备数量和种类的增加，任务规划也将越来越复杂[15]。通过规划希望达到多个最优的目标，提出了一种基于多目标任务规划算法和作战仿真相结合的框架用于辅助决策。研究了该框架在空中作战领域的几个部分，包括动态目标打击、情报侦察探测和无人机任务规划。在进化算法的研究领域，还可以做很多改进。希望这些工作能够被应用于实践，极大地帮助任务规划者。