一种用于仿生导航无人机航姿求解的混合滤波方法

金仁成，谢林达，魏 巍，蔚彦昭

(大连理工大学机械工程学院，大连 116024)

0 引言

近年来小型无人飞行器(Unmanned Aerial Vehicle, UAV)发展迅速，尤其在军事侦察、农业监测和救灾巡检等领域应用广泛[1-3]。事实上小型无人飞行器成本有限，在一定程度上限制了激光陀螺和光纤陀螺等高精度姿态测量装置的应用，于是体积小、质量小、集成度高、功耗低的微机电系统(Micro-Electro-Mechanical Systems, MEMS)成为执行导航任务的最佳选择[4-6]。由MEMS传感器组成的微型惯性测量单元(Micro Inertial Measurement Unit, MIMU)是MEMS的重要分支，通常包括角速度陀螺仪和加速度计。虽然惯性器件和导航技术得到了飞速发展,但是单纯依靠提高惯性仪表精度来改善导航系统性能不仅需要较高的技术水平，同时研发成本也相应提升。因此，现有方案大多以惯性导航为主体，结合其他导航设备形成组合导航系统，并利用无误差积累效应的外部参考信息源对惯性器件误差项实现补偿修正。现阶段普遍采取的组合导航方案是惯性/卫星组合导航技术[7-8]，但是卫星信号易被干扰甚至欺骗，导致无法执行导航任务以及存在无人飞行器被诱捕的危险。同时惯性/地磁组合导航技术也是常用方法[9-10]，该方式通过感知地球磁场强度分布提供导航所需信息。然而由于地表附近存在周期变化的磁场异常现象，影响了地磁场数据库构建精度，导致地磁匹配效果不佳。而且通过感应地球磁场方向提供航向信息的电子罗盘，极易受到周围电磁环境影响，无法给出准确测量结果。

针对上述问题，不仅需要准确性高、性能优良的姿态融合算法，同时设计一种自主性好、误差不累积、抗电磁干扰能力强的导航系统更是起到关键性作用。近年来仿生学逐渐成为热点研究内容，自然界中蟋蟀、蜻蜓、蝴蝶等生物巧妙利用天空中大气偏振模式实现精确导航的现象被人们发现[11-13]。国外学者Rayleigh等通过对太阳光偏振现象的分析论证，建立了著名的Rayleigh散射模型。随后Lambrinos等仿照沙蚁复眼结构，将偏振光敏感策略应用于机器人平台以提取偏振方向信息，实验结果表明输出的角度值不存在累积误差[14]。通过研究偏振光导航机理，国内的大连理工大学褚金奎教授团队率先研制出新型偏振光传感器，并利用地面移动机器人成功完成导航寻迹任务，验证了偏振光信息用于导航定向的可行性[15]。针对偏振光组合导航算法，哈尔滨工业大学通过仿真实验证明了偏振光信息能够修正惯性导航器件的姿态误差[16]。同时国防科技大学基于标准大气偏振模型推导了三维空间中航向角的计算方法，并仿真分析了各项误差源对航向角估计误差的影响[17]。

目前，国内外偏振光导航方面的研究主要集中在地面导航领域，无人机导航方面研究较少。现阶段偏振光导航策略主要是基于卡尔曼滤波的偏振光辅助定姿方法。然而利用卡尔曼滤波模型实现数据融合的每次迭代过程中其计算量相对较大，实时性难以保证，同时偏振光传感器的模型误差受多种因素影响不易确定。因此，通常利用卡尔曼滤波进行仿真分析[18-19]，同时由于仿真条件比较理想化，在实际导航环境中的应用效果不佳。

本文针对现有技术不足，设计了一种用于仿生导航无人机航姿求解的混合滤波方法。通过Mahony滤波对存在低频噪声的陀螺仪与易受高频噪声干扰的偏振光传感器及加速度计实现初步数据融合，再将获得的姿态信息作为系统观测量，并结合扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法构建混合滤波模型，以实现传感器数据的深度融合，最终输出精度更高的航姿求解结果。

1 偏振光分布模式及传感器测量模型

1.1 偏振光分布模式

在晴朗天气条件下，太阳光穿过大气层遇到大气中的空气分子和气溶胶粒子时，其光波振动方向会发生改变，从而在整个天空范围内形成相对稳定的大气偏振模式[20]。根据Rayleigh散射理论模型，该种模式与太阳空间位置和观测者所在位置密切相关，并在日地相对转动过程中保持稳定分布。

近年来国内外学者研究分析了生物的偏振视觉结构，建立了理想大气环境下的天空光偏振分布模型，这里采用天球模型[21]进行相应描述，天空光偏振分布模式如图1所示。图1中，O点代表偏振光传感器所在位置，S点代表太阳在天球模型上投影位置，Z点表示天顶位置(偏振光传感器所在位置正上方与天球交点)，SM为太阳子午线(通过S点和Z点的弧线)，ASM为逆太阳子午线。模型中的短线表示偏振矢量，短线的粗细表示偏振矢量强度，短线的切线方向表示偏振矢量方向。

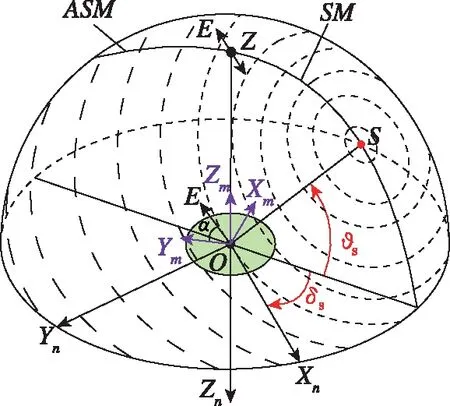
图1 天空光偏振分布模式Fig.1 Polarization distribution mode of skylight

1.2 偏振光传感器测量模型

本文偏振光传感器输出的偏振方位角φ是偏振矢量方向与传感器参考轴方向之间的夹角。这里定义偏振光模块坐标系为m系，并根据偏振光传感器量测输出值获得偏振矢量在m系中的投影为

(1)

图1中，Xm轴表示偏振光传感器参考轴方向，同时该方向也是传感器内偏振片安装基准，Zm轴表示偏振光传感器观测方向，这里O-XmYmZm构成笛卡尔右手坐标系。O点与S点连线为太阳矢量方向，这里用ϑs与δs分别表示太阳高度角和太阳方位角，则有太阳矢量在导航坐标系下的投影为

(2)

根据Rayleigh散射模型原理，偏振矢量方向总是垂直于太阳入射方向与观测方向所确定的平面，由此计算偏振矢量在m系中的解析式为

(3)

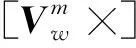
2 仿生导航混合滤波方法设计

虽然单独利用陀螺仪解算姿态角短时间内精度较高，但长期工作受漂移误差影响严重，同时考虑到传统卡尔曼滤波数据融合算法的局限性，本文设计了基于偏振光的混合滤波模型，并采用级联式框架结构。前一阶段利用偏振光传感器和加速度计低频特性良好的优势，与不易受高频噪声干扰的陀螺仪组建Mahony滤波模型，再结合EKF算法将获得信息作为后一阶段的系统观测量，构成偏振光混合滤波模型(Polarization Hybrid Filter, PHF) ，实现偏振光与惯性量测信息的深层融合，以获得高精度姿态解算结果。根据上述分析，本文设计的仿生导航混合滤波姿态估计方法原理图如图2所示。

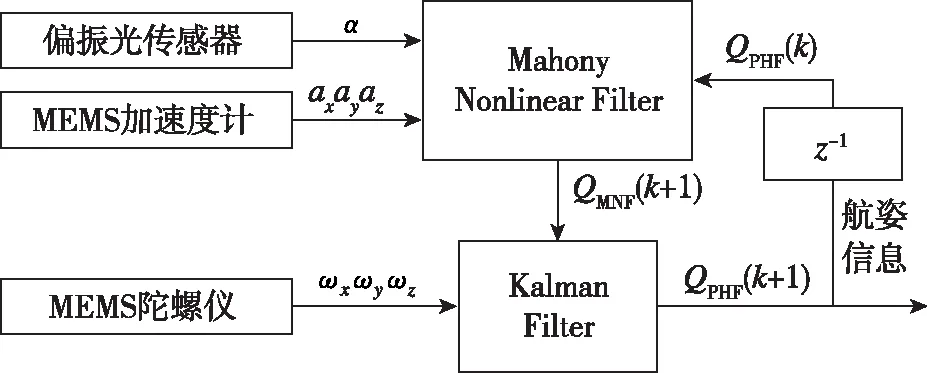
图2 混合滤波姿态估计方法原理图Fig.2 Schematic diagram of hybrid filter attitude estimation method

2.1 基于Mahony滤波的航姿求解方法

澳大利亚学者Robert Mahony提出的滤波算法是一种基于传感器频率特性的数据融合方法[22]。本文利用低频信号稳定的偏振光传感器与加速度计校正陀螺仪漂移误差，获得初步的姿态估计值。

本文的Mahony滤波模型将偏振光传感器和加速度计量测值作为前馈输入量，通过PI(比例-积分)反馈控制器实现对陀螺仪积分误差的补偿修正。基于大气偏振模式的Mahony滤波算法流程图如图3所示。

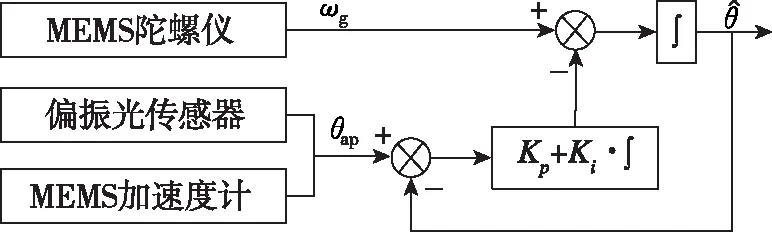
图3 Mahony滤波算法流程图Fig.3 Schematic diagram of the Mahony filter for attitude determination

根据图3可知，经过Mahony滤波后的姿态角估计值可表示为

(4)

(5)

(6)

(7)

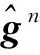
(8)

将总偏差矢量e输入PI反馈控制器得到误差补偿项，再对陀螺仪量测角速度进行校正，获得修正后的角速度值如式(9)所示。

(9)

(10)

式中，γ、θ、ψ分别代表航姿参考系统(Attitude and Heading Reference System, AHRS)中横滚角、俯仰角与航向角。

2.2 融合EKF的混合滤波姿态解算方法

小型无人机姿态变化是非线性的，因此采用EKF对其状态进行线性最小方差估计，通过预测及状态更新过程获得机体姿态最优估计值。

(1)状态量与状态方程的选取及建立

本文选取3个姿态值作为非线性系统状态量，并建立系统状态方程。设系统状态量为

(11)

式中，γ(k)、θ(k)、ψ(k)为k时刻横滚角、俯仰角与航向角的姿态值，并利用状态量建立如下系统状态方程

X(k)=f(X(k-1),k-1)+G(k-1)W(k-1)

(12)

式中，G(k-1)为系统噪声驱动矩阵，W(k-1)为系统过程噪声矩阵。对f(X(k-1),k-1)求雅可比矩阵可得系统状态转移矩阵为

(13)

(2)观测量与观测方程的选取及建立

考虑到观测量的误差精度直接影响卡尔曼滤波整体效果，因此观测量的选取成为卡尔曼滤波器设计的关键。本文考虑到偏振光传感器和加速度计易受机体振动等高频噪声干扰，而经过Mahony滤波后的传感器融合数据精度相对较高，因此本文将前一阶段降噪后的姿态估计值作为非线性系统观测量，设系统观测量为

(14)

式中，γap(k)、θap(k)、ψap(k)为k时刻Mahony滤波求解的横滚角、俯仰角与航向角数值，并利用观测量建立如下系统观测方程

Z(k)=h(X(k),k)+V(k)

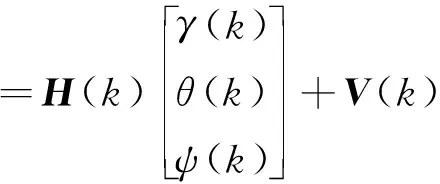
(15)

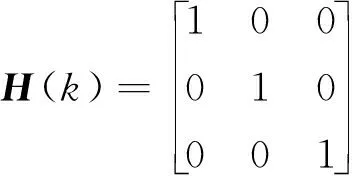
(3)卡尔曼滤波算法更新过程

1)基于状态转移矩阵的状态预测方程为

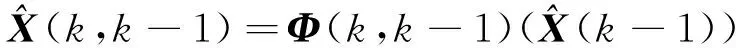
(16)

2)状态预测协方差矩阵为

P(k,k-1)=Φ(k,k-1)P(k-1)·

ΦT(k,k-1)+Q(k)

(17)

式中，P(k,k-1)为状态协方差矩阵的估计，Q(k)为系统噪声协方差矩阵。

3)卡尔曼滤波增益更新方程为

K(k)=P(k,k-1)HT(k)[H(k)P(k,k-1)·

HT(k)+R(k)]-1

(18)

式中，K(k)为滤波增益矩阵，H(k)为系统量测矩阵，R(k)为观测噪声协方差矩阵。

4)系统状态更新方程为

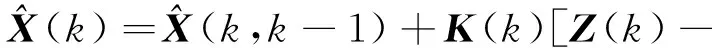
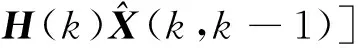
(19)

5)状态协方差矩阵更新方程为

P(k)=[I-K(k)H(k)]P(k,k-1)

(20)

将Mahony滤波降噪后的航姿数据作为后一阶段的系统观测量，采用与EKF模型相结合的级联式滤波算法，实现对偏振光传感器与IMU输出信息的深层融合，从而获得高精度的姿态估计结果。

3 算法验证与测试分析

基于偏振光的AHRS由IMU与偏振光传感器组成。这里采用开源Lisa/M飞行控制系统输出的姿态信息作为算法验证的参考值，其中主要包含IMU MPU-6050与电子罗盘 HMC5883L等电子器件。为了评估本文提出的混合滤波方法的性能，在静态与动态不同实验环境下进行测试，并与基于电子罗盘的EKF航姿参考值进行比较。本文搭建的偏振光导航实验平台如图4所示。

图4 偏振光导航实验平台Fig.4 Experiment platform of polarized-light navigation

3.1 静态环境验证分析

由于偏振光分布模式与开展实验的时间及地点密切相关，因此这里给出详细信息。本次静态实验从2018年6月20日17点50分开始，持续约250s，且当时当地的太阳高度角为16.31°，太阳方位角为-107.24°。将本文提出的航姿求解混合滤波PHF方法与飞控系统标准EKF方法以及单独采用Mahony滤波融合偏振光数据的最小噪声分离(Minimum Noise Fraction，MNF)方法进行比较分析，姿态角对比曲线如图5所示。同时为表明不同方法之间的差异，静态环境姿态角均方差结果如表1所示。

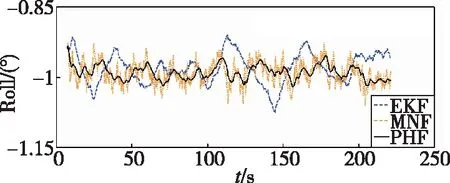
(a) Roll-γ

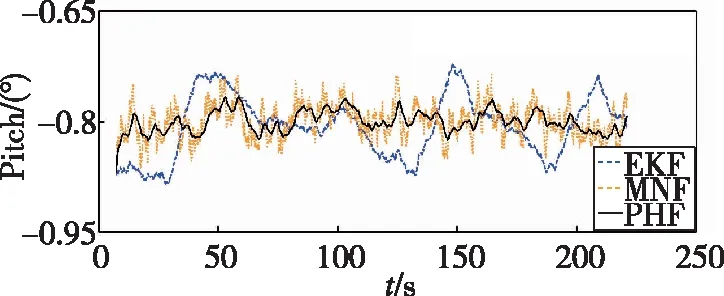
(b) Pitch-θ

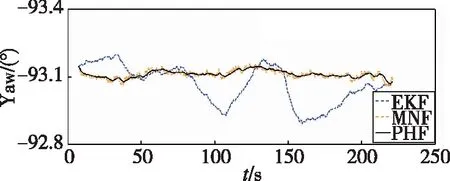
(c) Yaw-ψ图5 静态环境姿态角测试结果Fig.5 Static test results of attitude determination

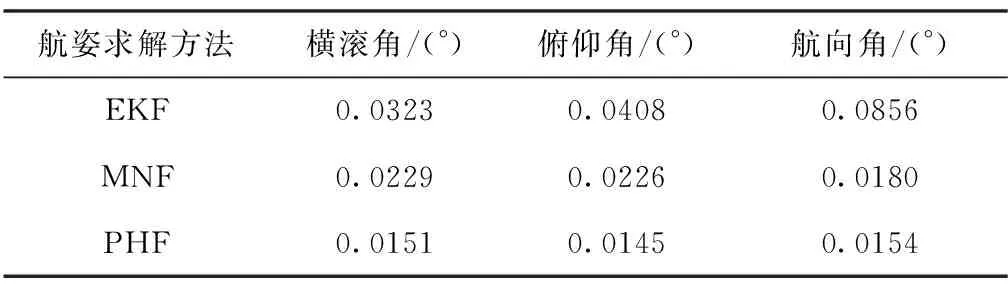
航姿求解方法横滚角/(°)俯仰角/(°)航向角/(°)EKF0.03230.04080.0856MNF0.02290.02260.0180PHF0.01510.01450.0154

图5中，基于偏振光的Mahony滤波方法与本文设计的混合滤波方法均能有效抑制陀螺仪漂移误差，但是MNF方法不能有效消除偏振光传感器内部噪声，导致姿态角曲线抖动明显。相比之下,本文提出的PHF方法能有效抑制内部噪声干扰。表1中，基于偏振光的两种方法较基于电子罗盘的EKF算法的姿态角均方差更小，表明新型惯性/偏振光组合导航系统的抗随机噪声干扰能力更强。同时相较于EKF算法，本文提出的PHF方法表现出更高的静态精度，其中横滚角提高53.3%，俯仰角提高64.5%，航向角提高82.0%，可见PHF方法的静态稳定性更高，有利于无人机导航系统的自主调整与控制。

3.2 动态环境验证分析

本次实验主要考虑倾斜运动环境下算法的适应性。实验地点不变，实验时间为2018年6月20日18点35分，其中太阳高度角为8.10°，太阳方位角为-113.65°。将本文设计的PHF方法与飞控系统参考EKF方法和MNF方法进行比较分析，姿态角对比曲线如图6所示。

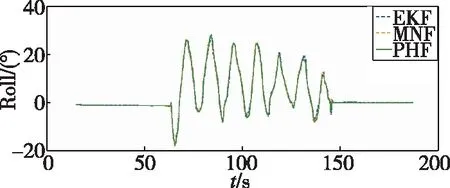
(a) Roll-γ

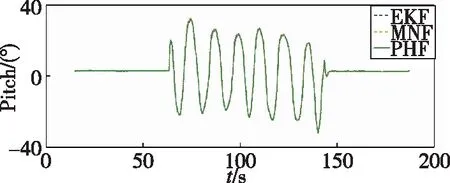
(b) Pitch-θ

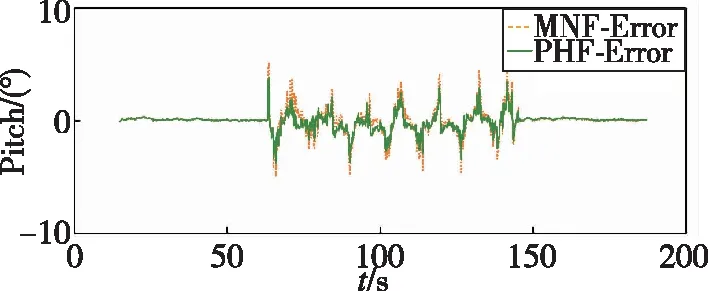
为表明PHF方法与MNF方法求解姿态信息的准确性，两种方法的姿态值估计误差如图7所示，其估计误差范围如表2所示。

(a) Roll-γ

(b) Pitch-θ

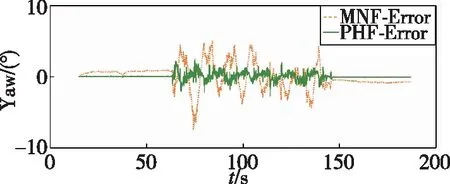
(c) Yaw-ψ图7 动态环境姿态值估计误差Fig.7 Attitude estimation error in the dynamic test

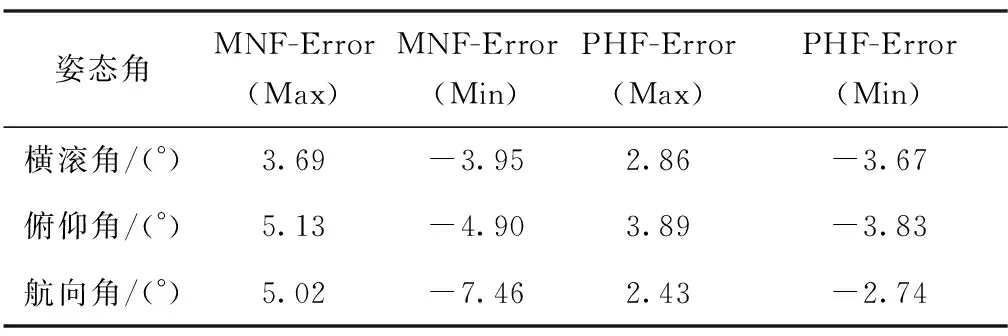
姿态角MNF-Error(Max)MNF-Error(Min)PHF-Error(Max)PHF-Error(Min)横滚角/(°)3.69-3.952.86-3.67俯仰角/(°)5.13-4.903.89-3.83航向角/(°)5.02-7.462.43-2.74

图6中，利用MNF方法求解航姿时存在超调现象，主要是由于该方法响应速度较慢，导致对姿态变化的敏感性较差。相比之下，本文提出的PHF方法的姿态跟踪效果更好、响应更及时、可靠性更高。同时，从图7的误差曲线可以看出，采用PHF方法所求解的姿态角误差值较MNF方法更小。根据表2数据可知，在动态环境中利用PHF方法求解的航姿精度更高，其姿态值估计误差控制在±4°范围内，与MNF方法±8°的误差范围相比，混合滤波方法显著提高了偏振光组合导航系统姿态估计的动态精度，保证了倾斜运动条件下姿态解算的准确性。

4 结论

考虑到传统组合导航系统的局限性，本文引入了无误差累积效应、自主性好、抗电磁干扰能力强的偏振光传感器与惯导构成新型仿生组合导航系统。同时针对现有偏振光导航姿态求解方法精度不高的问题，设计了一种用于仿生导航无人机航姿求解的混合滤波方法，并在不同环境中进行了测试分析。

经过与Mahony滤波方法以及融合电子罗盘数据的EKF算法姿态解算结果比较可知，本文的混合滤波方法能够更大限度地消除偏振光传感器内部噪声干扰，静态定姿精度普遍提高了50%以上，且航向角定姿精度提升尤为显著，达到了82%。同时在动态情况下，混合滤波方法克服了Mahony滤波的姿态估计超调问题，表现出更好的跟踪效果和更快的响应速度，提高了偏振光组合导航系统的动态定姿精度，保证了无人机系统控制输出的准确性和可靠性。但本文实验大多选择晴朗无云的天气条件开展，以避免多次散射的不利影响，下一步工作将研究不同天气条件下天空光的偏振模型，以提高偏振光组合导航系统对复杂天气环境的适应能力。