多传感器协同探测证据理论分类融合方法

蒋 雯，张 瑜，谢春禾

(西北工业大学电子信息学院，西安 710129)

0 引言

现代战场环境具有电磁信号密集度高、作战环境立体化、威胁目标多方位等特点[1]，在这样的复杂场景下，武器对目标的精确打击难度不断提升。对于精确制导武器而言，传统的基于单一传感器或传感器平台的探测感知系统已经难以满足现代作战任务的需求。多传感器协同探测成为导弹武器应对复杂场景目标检测识别、增强战场环境智能感知能力和提升干扰对抗能力的重要技术手段[2]。针对不同的探测任务背景和作战需求，多传感器协同探测包含雷达、光电、红外等多种探测传感设备。此外，为了获取更高的探测性能与能力，多传感器协同除了利用武器本身搭载的探测设备外，还可以跨域整合陆基、空基、天基等多种探测平台。

多传感器协同探测的关键在于多源信息融合理论[3-4]，其中值得关注的一点是信息的可靠性及准确性是参差不齐的[5]，这也导致盲目地将所有传感器的数据进行直接融合的结果并不总是优良的[6-8]，可能会受到少部分的干扰或错误信息影响进而出现不理想的结果。因此，对融合之前的信息有效性及将其进行融合是否合适，以及对信息融合之后的有效性进行合理分析与度量是很有必要的。

证据理论是一种主要侧重于特征级融合与决策级融合的统计推理方法[9]，至今已有50余年的发展历史。该理论把概率论中的基本事件空间拓宽为基本事件空间的幂集(又称为辨识框架，Frame of Discernment，FOD)，在辨识框架上建立基本概率指派函数(Basic Probability Assignment，BPA)来描述不确定信息。特别地，当BPA中的信度只在辨识框架的单子集命题上进行分配时，BPA就等价为概率论中的概率，而组合规则退化为概率论中的Bayes公式。从这个角度来看，证据理论在简单的环境中向下兼容概率论，而在复杂模型下能够有效地表示和处理不确定信息，这些特点使其在多源信息融合领域得到了广泛的应用[10-12]。

在证据理论框架体系下，对信息融合的研究主要集中在BPA合理生成[13-15]、证据冲突处理[16]、计算复杂度问题[17]等方面，这些研究对提升信息融合结果的可靠性奠定了一定的基础。但是在信息融合领域，仍然缺少对信息融合质量的判别研究。如果信息质量低下，又缺乏信息的质量评估和质量控制机制，可能导致融合出现错误的结果。因此，多传感器协同探测时需要建立一种有效的信息融合质量判别方案，提升目标识别准确率。对此，本文将以证据理论体系为框架，探讨多传感器协同探测时融合信息的筛选方法与信息融合有效性的度量方法。

1 理论基础

利用证据理论对多传感器的探测信息进行融合，必然需要将探测信息转化为证据表示并融合。此外，为了衡量融合的有效性，需要对融合过程中信息的不确定度进行度量。本节介绍了一些基础理论。

1.1 证据理论

Dempster-Shafer证据理论也叫证据理论或者D-S证据理论[18-19]，是由Dempster和Shafer在20世纪60年代末70年代初建立的一套数学理论。这套数学理论进一步扩展了概率论，最早用于专家系统，还适用于故障诊断、模式识别、人工智能以及系统决策等，是一种有效的融合方法。

多传感器协同探测时，所有可能的目标类型共同构成了D-S证据理论中的辨识框架。可设Θ={d1,d2,…,di,…,dn}是辨识框架，辨识框架中的n个元素都是两两互斥的。当一个命题对应辨识框架中的一个子集时，则称辨识框架识别到了这个命题。Θ的幂集2Θ所构成的2N个元素的集合为

2Θ={d1,d2,…,dN,d1∪d2,d1∪d3,…,Θ,∅}

证据理论中的所有元素及命题均为该幂集的子集，如依据传感器的探测信息，可以识别目标为{d1}或者{d1,d2}。

证据理论是用BPA来描述命题信任度分配，表示证据对某一命题的支持度。BPA的定义如下：

设Θ是辨识框架，其幂集构成命题集合2Θ,∀A⊆Θ，若函数m∶2Θ→[0,1]满足式(1)

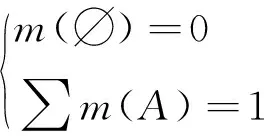
(1)

则称m为一个BPA。式中：m(A)为命题A的基本概率指派，表示准确分配给A的信任度。

D-S证据理论提供了Dempster组合规则来自多个独立信息源的信息，它的本质是证据的正交和。设有2条证据的基本概率指派分别为m1和m2，对应的焦元分别为A1,A2,…,Ak和B1,B2,…,Bl，Dempster组合规则如下

(2)

式中

(3)

用于衡量证据间的冲突程度，K越大则冲突越大。

1.2 Deng熵

战场环境中，敌我双方会设置各种电磁干扰等对抗措施，可能导致传感器的探测信息存在不确定性或虚假目标等，因此，需要对探测信息进行有效分析。借鉴热力学中对系统无序状态度量的熵概念，克劳德·香农在信息论中定义了信息熵，用以衡量信息的冗余性或者不确定度。然而它并不适用于证据理论，因为证据理论中存在多子集命题，即依据探测信息可能同时识别为多个目标类型。一些学者对信息熵进行推广及修改后将其应用于证据理论领域，但它们均存在一些不足。

Deng熵[20]是邓勇提出的一种度量BPA不确定度的信度熵。随着辨识框架内基本元素数的增加，它的值能够相应增大，也就是说，焦元中元素的个数越多意味着不确定程度越高。并且在BPA中命题均为单子集命题时，能够退化为获得广泛认可的香农信息熵，这些特性使得Deng熵在度量BPA不确定性方面具有一定的优势。Deng熵定义如下

(4)

式中：m是定义在辨识框架X上的BPA，A是BPA中的焦元，|A|是A的势，即A中元素的个数。

因此，若基于Deng熵对多传感器协同探测信息进行筛选，可实现各类别内信息的有效融合，使融合过程向熵减的方向进行，克服了直接融合所有信息可能产生的缺陷，提出了一种证据分类融合算法。

2 证据理论分类融合算法

多传感器协同探测时必然产生关于目标的多条探测信息，而由于目标所处环境的复杂性与不同类型传感器本身存在的局限性等，使得这些多源信息具有不确定性或不精确性等特点。在信息处理领域，熵能够衡量一个随机变量的不确定程度或信息量的大小。对于一条已知信息(证据理论体系下即为证据，BPA)，它的信息熵越大代表信息越不确定，消解不确定度所需要的信息量也越大。换言之，在信息融合的过程中必然伴随着证据体的信息熵的增减变化。若通过信息融合算法，使得原有证据的信度熵减小了，表明融合过程降低了信息的不确定性，从融合结果中获取了相比于原始信息更多的信息量；并且较低的信息熵意味着更低的决策难度。另一方面，信度熵的变化与待融合证据的冲突大小存在一定关系。导致冲突的主要原因是不同的证据各自支持不同的主焦元。而根据Dempster组合规则的特点，彼此之间冲突的证据在组合之后的信度分配将会变得均匀，导致信度熵增大；但冲突较小适于融合的证据在融合后将对主焦元进行聚焦，信度熵一般是降低的，更加利于决策。综上所述，一个有效的信息融合过程应伴随着证据体信息熵的降低。

就证据理论体系中的熵而言，Deng熵具有一些优良的特性，例如Deng熵随命题集合的势变化同向单调变化，随辨识框架的变化同向单调变化，当BPA退化为概率时，Deng熵等价于香农信息熵。因此本文采用Deng熵作为信息融合过程的有效性判别标准。2条证据融合后的证据的Deng熵若小于融合前的2个熵值，则认为该次融合是有效的，能够提升决策质量与信息可靠性，应予保留，反之则考虑放弃该次融合。如果1条证据与其余所有证据的融合均是无效的，那么表明这条证据自身很有可能是错误的，应当将其剔除。

具体的信息筛选及分组融合方法步骤如下：

1)对N条待融合的证据，任选一条m1作为起始证据，对其余N-1条证据，逐一输入证据与m1融合，若某一条(例如m2)的融合结果m12的熵小于融合前2条证据的熵，则表示这2条证据适合融合，融合结果有助于进行决策，可以进行融合，之后对N-2条证据继续融合；若不满足熵减原则，则输出m2，然后判定其余证据与m1融合是否满足熵减，以此类推，直至遍历所有N-1条证据完成此轮融合。步骤结果为输出符合融合要求的i条证据(包含m1)的融合结果，以及不满足要求被分离出的N-i条证据。其中i条证据间融合时满足熵减规则，同时剩余N-i条证据，进入下一步骤。

2)将剩余N-i条证据作为待融合证据，重复上一步骤，得到j条满足熵减原则的证据，以及N-i-j条待融合证据，完成此轮融合并进入下一步。

3)重复上述步骤，直至将N条证据全部完成分类，没有证据剩余。

该算法保留了证据理论中Dempster组合规则具有交换律及结合律的优点，使得融合顺序的变化不会影响分类结果及融合结果。在决策时，可以认为将含有证据数最多的类别融合结果作为总体融合结果是最准确和最有效的。因为它能够避免高冲突证据的影响，提升信息融合的可靠性与有效性。

3 仿真校验

本节将通过一个算例，说明本文所提算法的具体实现方法与有效性度量。

例：假设多传感器协同探测目标a、b、c，共产生6条探测信息，转化至证据理论框架体系，即辨识框架{a,b,c}下有6条待融合的证据BPA分别如下

m1∶m(a)=0.85,m(ac)=0.05,m(abc)=0.1
m2∶m(a)=0.8,m(ac)=0.15,m(abc)=0.05
m3∶m(b)=0.85,m(bc)=0.1,m(abc)=0.05
m4∶m(a)=0.7,m(ac)=0.2,m(abc)=0.1
m5∶m(b)=0.87,m(bc)=0.08,m(abc)=0.05
m6∶m(c)=0.75,m(bc)=0.15,m(abc)=0.1

首先通过观察可以发现，例中的6条证据存在较大程度的冲突，直观上按照主焦元的不同可以将上述BPA大致分为3类：第一类为1、2、4，它们强烈支持目标a；第二类为3、5，支持目标b；第三类为6，支持目标c。第一轮的证据分类过程如图1所示。

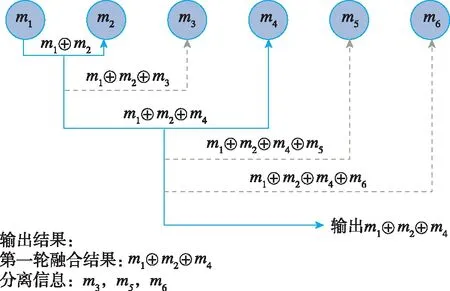
图1 第一轮分类融合结果Fig.1 Classification fusion results of the first round

从图1中可以看到，第一轮分类融合将证据1、2、4分为一类并进行融合，余下3条证据进入下一轮的分类，如图2所示。

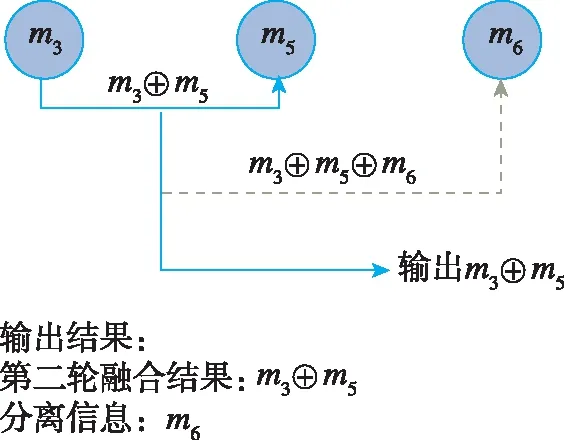
图2 第二轮分类融合结果Fig.2 Classification fusion results of the second round

从图2可以看出，第二轮融合将证据3、5作为一类并进行融合，余下证据6为第三轮的融合。更进一步地，在分类融合中各融合证据的Deng熵变化情况如表1所示。

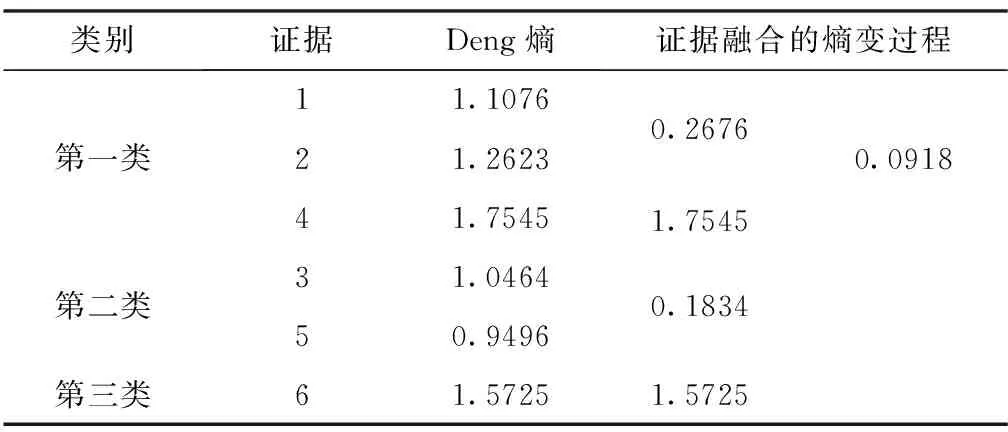
表1 分类融合Deng熵的变化过程

由表1可以看到，类别内部在融合时均能够保证Deng熵降低，从而提高信息的可靠性及决策的容易程度。这表明分类融合算法是有效的，最终的3类证据各自的融合结果如下

m124∶m(a)=0.991,m(ac)=0.0085,
m(abc)=0.0005
m35∶m(b)=0.9805,m(bc)=0.017,
m(abc)=0.0025
m6∶m(c)=0.75,m(bc)=0.25

分类算法将原始的6条证据划分为了3类，在各自类别中的融合结果的熵值是比较小的，这也能够从融合结果中直观地体现，融合结果的信度分配都比较突出，主命题的信度相当高，因此能够较方便地进行决策。在多个类别之间进行筛选时，根据少数服从多数的原则，采取具有最多数量的类别融合结果作为总体融合结果，即m124，因此，可判断多传感器协同探测的结果为目标a。

而将原始证据直接采取Dempster组合规则进行融合得到的结果为

m(a)=0.4539,m(b)=0.2246,
m(c)=0.3132,
m(ac)=0.0039,m(bc)=0.0042,
m(abc)=0.0002

两者对比可以看到，直接采用Dempster组合规则的融合结果中，目标a的信度最大，但是仍不足0.5，这样在决策时会产生困难；另一方面融合结果的熵值为1.6，不仅远高于分类融合的融合结果，甚至高于融合前除证据4外的其余证据，这表明经典的Dempster组合规则可能会导致信息不确定性的增加，即便能够得到正确的结果，也不利于决策，不是高效的融合过程。

当m6支持目标b时，即算例中第6条证据为m(b)=0.75,m(bc)=0.15,m(abc)=0.1，则算例中的6条证据可以分为2类：第一类为1、2、4，它们强烈支持目标a；第二类为3、5、6，它们强烈支持目标b。此时，依据本文所提出的证据分类融合算法，分类融合结果如下

m124∶m(a)=0.991,m(ac)=0.0085,
m(abc)=0.0005
m356∶m(b)=0.9951,m(bc)=0.0046,
m(abc)=0.0003

融合过程中熵值变化如表2所示。

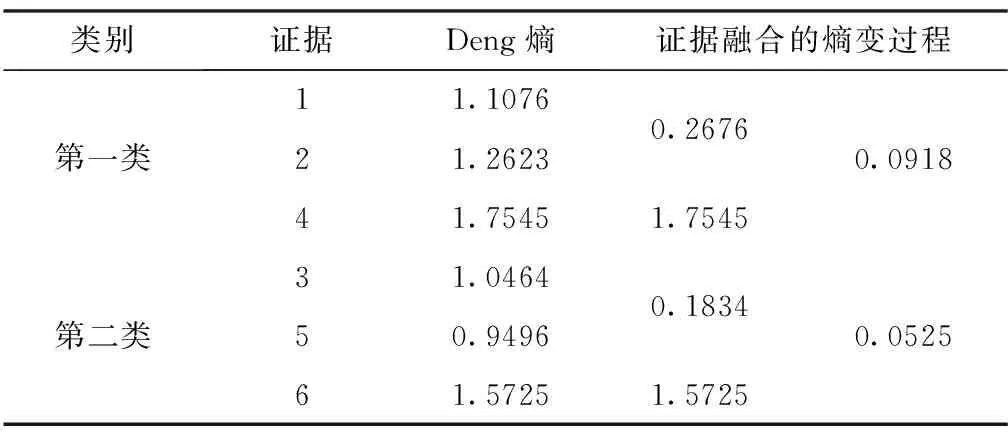
表2 分类融合Deng熵的变化过程

表2中，两类证据的数量相同，仅依靠少数服从多数的原则难以判断目标类型。由于熵值表示信息不确定程度，熵值越小，信息的确定度越高，因此可以结合证据融合后的熵值判断目标类型。由表2可以得到，第二类证据融合后熵值为0.0525，相比于第一类证据融合后的熵值0.0918更小，即信息的确定性程度更高。因此，此时可以判断多传感器协同探测的结果为目标b。

此种情况下直接采用Dempster组合规则融合可以得到

m(a)=0.3139,m(b)=0.6305,
m(c)=0.0498,
m(ac)=0.0027,m(bc)=0.0029,
m(abc)=0.0002

依据直接融合的结果也可以判断多传感器协同探测的结果为目标b，与本文提出的证据分类融合方法结果一致。

本文所介绍的分类融合算法，分类结果与证据输入顺序无关，并且能够得到不确定性低、可靠度高的证据融合结果。通过有效性度量与控制，实现了对证据的分类融合，降低了多传感器协同探测时的决策困难。此外，相比于直接采用Dempster组合规则融合的方法，本文所提出的证据分类融合方法所需的融合次数更少。

4 结论

本文提出了一种基于Deng熵的证据理论分类融合算法，以熵减为主要思想，将证据进行分类融合。在决策时，将含有证据数最多的类别融合结果作为总体融合结果，避免了高冲突证据的影响，提升了融合结果的信息有效性，增加了多传感器协同探测的准确率。并采用算例说明了所提方法不仅能够得到合理正确的结果，并且融合可靠性较高，便于决策与后续的信息处理。

未来与展望：在本文的试验中发现，虽然熵能够反映信息的有效性与可靠度，但仅通过熵减原则来判断融合是否有效存在一定的不足，且随着信息量的增加，实际应用时存在计算复杂度骤增的可能。今后将考虑完善信息融合有效性的判别准则，另外在将证据分类之后，对多个组内的融合结果可以尝试进行二次融合，尽可能多地利用原始证据中的信息，使得多传感器协同探测得到更加准确全面的结果。