基于CDKF的快速协方差交叉融合跟踪算法研究

宋 闯，张 航，郝明瑞

(复杂系统控制与智能协同技术重点实验室，北京 100074)

0 引言

随着科技的不断进步和武器装备的快速发展，战场环境日益复杂，武器装备面临严峻挑战，必须提高其抗干扰性能和精确制导能力。而传统单一模式制导的方式已很难满足上述需求，因此，必须要研究基于多传感器信息融合的制导技术，才能更好地发挥导弹武器的作战效能。制导信息需要通过对目标进行跟踪估计得到。

跟踪估计方法主要有扩展卡尔曼滤波(Extended Kalman Filter，EKF)和Sigma点卡尔曼滤波(Sigma-Point Kalman Filter，SPKF)。EKF是最早提出的非线性滤波算法，并得到了广泛的应用。但该算法有明显的缺点：需要得到系统的解析形式来计算雅克比矩阵，以及在非线性较强的情况下估计精度下降明显。SPKF算法利用加权统计线性回归技术，通过Sigma点的选取和变换来近似状态和均值的非线性变换，对高斯分布而言，均值和方差的近似可以达到3阶(泰勒展开)精度[1]。根据采样点选取策略的不同，SPKF算法包括无迹卡尔曼滤波(Unscented Kalman Filter，UKF)和中心差分卡尔曼滤波(Central Difference Kalman Filter，CDKF)算法[2]。

对于分布式融合系统，冗余信息的多重利用往往会降低系统的融合性能，传统的贝叶斯估计方法很难处理这一问题。针对这种情况，J.K.Uhlmann等[3]提出了一种可应用于任意复杂分布式系统的协方差交叉(Covariance Intersection，CI)融合算法，当局部状态估计满足一致性估计的条件时，算法所得融合估计也能保证估计的一致性。CI算法需要计算非线性评价函数的极值，这是一个很大的缺陷。因此，文献[4]提出了一种非迭代的快速协方差交叉(Fast Covariance Intersection，FCI)算法。

本文针对多传感器分布式融合跟踪问题，提出了一种基于CDKF和FCI的融合跟踪算法。局部传感器采用CDKF处理非线性变换问题，避免了求解复杂的雅克比矩阵。与邻近的其他传感器采用FCI算法对获得的信息进行融合处理并输出融合结果相比，保证了融合算法的实时性。最后将得到的融合估计反馈给局部传感器。该算法充分利用了CDKF和FCI的优点，仿真结果表明了该算法的有效性。

1 系统模型的建立

在多传感器目标跟踪融合过程中，每个传感器一般的系统方程为

(1)

式中，xk为nx维的系统状态向量，zk为第s个传感器的ny维观测向量。w为系统噪声，协方差矩阵为Q。vs为第s个传感器的观测噪声，协方差矩阵为Rs。假定w和vs都是互不相关的高斯白噪声，且都是加性噪声。针对目标跟踪问题，需要采用特定的系统模型，具体如下所述。

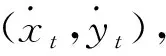
xk+1=Φxk+1+Γwk

(2)

式中，wk是均值为0的白噪声序列，Φ和Γ为转移矩阵。假设目标做近似匀速直线运动，则有

(3)

其中，T为采样时间，I2为2×2的单位阵。

假设第s个传感器对目标的观测为距离和方位角zs=[rs,θs]T，则有观测方程为

(4)

式中，Δxs=xt-xs，Δys=yt-ys，(xs,ys)为传感器位置坐标。

2 CI算法和FCI算法

2.1 CI算法[5-6,16]

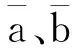
可以由一致性估计的定义得到

(5)

(6)

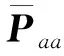
对于2个估计量的情况，CI算法可以总结如下

(7)

(8)

参数ω决定了估计的最优性，该参数可以根据Pcc某一范数最小的准则，通过最优化方法搜索得到。

2.2 FCI算法

相对于标准卡尔曼滤波算法而言，CI算法的特点是需要计算非线性评价函数的极值[9-15]。因此，需要发展一个非迭代的FCI算法。

在最小均方误差意义下的优化，如下所示。

(9)

需要迭代计算价值函数的最小值以求得相应的权重系数ωn。为了减小计算负担，采用下面一种次优的非迭代算法。

当N=2时，非负权重系数满足下面的线性约束。

ω1+ω2=1

(10)

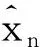
tr(P1)ω1-tr(P2)ω2=0

(11)

上面两式联立，可产生下面的线性系统

(12)

当满足tr(P1)+tr(P2)>0的条件时，上面的方程有唯一解

(13)

注意到tr(Pn)≥0保证了ωn≥0，进而满足0≤ωn≤1。

对于N≥2,有

(14)

ω1+ω2+…+ωN=1 0≤wn≤1

(15)

这里εn=tr(Pn)，对于任意tr(Pn)>0，权重系数ωn是唯一且非负的。

3 CDKF-FCI算法

CDKF利用一组确定的采样点来捕捉系统的充分统计量，从而可以估计状态变量经过任意非线性变换后的均值和方差。CDKF采用Sterling差值公式，利用中心差分代替泰勒展开中的前两阶导数

f′(x)=[f(x+h)-f(x-h)]/2h

(16)

f″(x)=[f(x+h)+f(x-h)-2f(x)]/h2

(17)

式中，h≥1是中心差分步长。

CDKF-FCI算法采用中心差分来近似非线性变换，同时利用FCI算法对其他传感器得到的信息进行融合处理，并将结果反馈给局部传感器。对于第s个局部传感器，算法流程具体如下：

1)初始化

(18)

2)计算时间更新Sigma点

(19)

3)时间更新

Sigma点随状态方程的传播为

(20)

状态的预测值和相应的误差方差阵为

(21)

(22)

4)计算量测更新的Sigma点

(23)

5)量测更新

Sigma点随量测方程的传播为

(24)

量测的预测值和相应的误差方差阵为

(25)

(26)

状态和量测的互协方差矩阵为

(27)

滤波增益为

(28)

量测残差为

(29)

后验状态和相应的误差方差阵为

(30)

(31)

式中

(32)

(33)

(34)

(35)

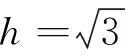
6)融合

得到局部传感器状态和误差方差阵后，计算融合后的状态和相应的误差方差阵为

(36)

(37)

式中

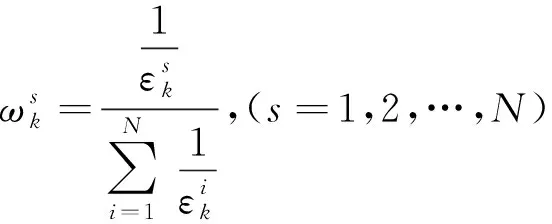
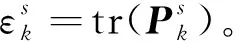
7)反馈

将局部传感器的状态和误差方差阵用融合后的结果替换为

(38)

(39)

4 仿真分析

为了验证算法的有效性，采用如下场景：目标初始位置为(1000,1000)m，以速度(100,10)m/s做匀速直线运动。共有2个传感器对目标进行观测，位置分别为(1900,3200)m和(3575,3425)m。状态方程和观测方程分别由式(2)和式(3)给出。传感器为主动传感器，可以观测角度和距离，其测距误差标准差为10m，测角误差标准差为0.2°，采样时间为1s。仿真时间50s。

为了进行性能比较，使用位置和速度的均方根误差(Root Mean Squared Error，RMSE)作为性能指标。k时刻的位置RMSE定义为

RMSEp(k)=

(40)

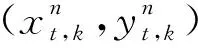
仿真中分别采用基于CI的CDKF-CI算法和本文提出的基于FCI的CDKF-FCI算法，进行100次蒙特卡罗仿真，结果如图1和图2所示。由图中可以看出，本文提出的CDKF-FCI算法较好地估计了系统的位置和速度，跟踪精度相比CDKF-CI算法也有较大的提高。结果表明所提出的方法具有较高的融合跟踪定位精度。

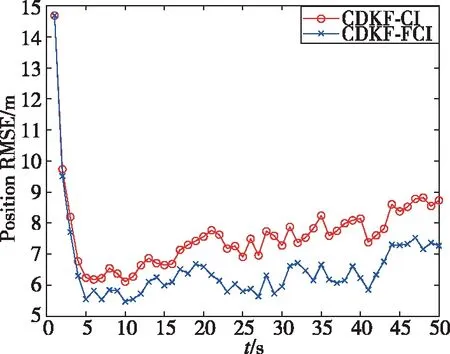
图1 位置的均方根误差Fig.1 RMS error of position

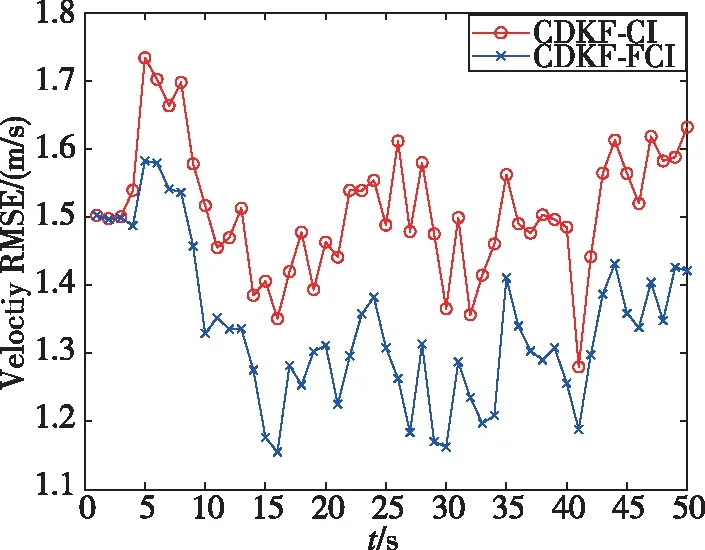
图2 速度的均方根误差Fig.2 RMS error of velocity

5 结论

本文提出了一种基于CDKF和FCI的融合跟踪算法，用于协同制导中的多个传感器对目标的跟踪定位，该算法与传统算法相比具有以下几点优势：

1)CDKF-FCI融合跟踪算法不需要计算复杂的雅克比矩阵，相比CI算法无需迭代优化过程，简化了融合系统的设计；

2)仿真结果有效地证明了CDKF-FCI融合跟踪算法具有较高的估计精度。