基于FPGA的自适应阵列协方差矩阵特征分解的实现
陈 静,祝娇娇,刘盛典,刘 鹏,徐振兴
(航天恒星科技有限公司,北京 102102)
0 引言
在电子信息快速发展的当今社会,卫星导航在军民应用领域占据越来越重要的地位,干扰和抗干扰技术的发展直接影响导航应用的有效精度[1]。而在抗干扰的过程中,对空间信号波达方向(Direction of Arrival,DOA)估计、干扰个数检测、最优权矢量的实现精度影响着导航接收机的抗干扰性能,协方差矩阵的特征分解是这些算法实现过程中的核心部分[2-4]。
本文根据自适应阵列天线获得的协方差矩阵性能,将复数阵列协方差矩阵的特征分解进行现场可编程门阵列(Field Programmable Gate Array,FPGA)实现,并通过将其应用于空间信号DOA估计进行验证。另外,在实现的过程中对直接调用CORDIC IP核的方式进行了精度误差分析,并用一种双精度浮点的方式进行修正,提高了FPGA矩阵特征分解实现精度。
1 阵列协方差矩阵特征分解
在抗干扰处理过程中,通常得到的数据是有限时间范围内的有限次快拍数。在这段时间内假定接收到的导航信号的方向不发生变化,或者认为导航信号的包络虽然随时间变化,但它是一个平稳随机的过程,其统计特性不随时间变化。而且天线的阵元个数大于干扰信号个数,干扰信号的方向向量是线性独立的,阵列中噪声具有高分布特性,所以接收机接收到的信号向量的协方差矩阵是对角非奇异阵,也是复数正定Hermite阵。
1.1 复数协方差矩阵转化为实矩阵
相对于实数计算,复数的处理增加了FPGA运算的复杂度,所以为了降低计算复杂度,在设计的过程中需将复数协方差矩阵转化为实数矩阵。
根据文献[5]将n阶协方差矩阵Rxx写成实数矩阵和虚数矩阵两部分,即
Rxx=A+iB
(1)
式中,A、B均为实矩阵。
由于协方差矩阵是复数正定Hermite阵,根据其性能可知
AT=A,BT=-B
(2)
设特征值为λ,对应的特征向量为U+iV,其中U、V均为n维实列向量,则有
(A+iB)(U+iV)=λ(U+iV)
(3)
根据式(3)可写为
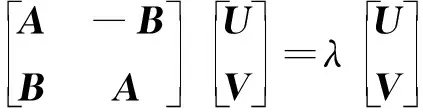
(4)

1.2 实数矩阵特征分解
经典的实数矩阵特征值计算算法中,雅克比(Jacobi)算法在同等计算精度要求下具有更快的速度[6-7],且具有并行计算的优势,可将分解过程划分为并行的子步骤同时进行。另外根据应用需求,需得到特征值对应的特征向量,而双边Jacobi的计算结果可以直接给出特征值对应的特征向量,所以采用双边Jacobi算法进行特征值和特征向量的FPGA实现。
Jacobi算法通过对实数矩阵S进行一系列平面旋转变换来产生一系列对称方阵Ak,每次旋转变换使Ak中的2个元素变为0[8]。当多次迭代后,Ak趋于一个对角阵D,D的各主对角元素就是S的特征值[9-10]。从Ak到Ak+1的旋转变换公式为

(5)

(6)
T的选择为

(7)
式中,p (8) 进行一次旋转变换,矩阵Ak相对于矩阵Ak-1变化了的元素是 (9) (10) (11) (12) Jacobi算法在每次进行旋转变换后,根据式(5)、式(7)可以看出,实对称矩阵的第p行、q列、q行、p列都发生了变化,变化结果如式(10)、式(11)所示,而矩阵的其他行、列的元素与变换前相应的元素相同,并不会发生变化。 利用这一特性,对于n×n的矩阵,在FPGA设计时可采用n/2个处理器并行处理的方法同时消去2n个非对角元素,一次迭代只需n-1步完成,减少了FPGA的运算时间。所以对于阵元数为M的阵列天线,协方差矩阵转化为2M×2M的实矩阵后,可采用M个处理器并行处理。但每次旋转后矩阵需按表1所示的规律进行行列交换,以确保新矩阵的正确性,一次迭代需进行2M-1次旋转和2M-1次行列交换。 表1 一次迭代处理器循环次数及行列交换规律 Jacobi算法求解实数矩阵S特征值和特征向量的具体步骤为: 1)初始化特征向量为单位阵E,即主对角线元素为1,其他元素为0; 2)根据式(12)计算tan2θ,求sinθ、cosθ及矩阵Tpq; 3)利用式(5)~式(6)计算得到A1,用当前特征向量矩阵E乘以矩阵Tpq得到特征向量V1; 5)若当前迭代前的矩阵A的非对角线元素中最大值小于给定的阈值e时,停止计算;否则,令A=A′1,V=V′1,重复执行步骤2)~5)。停止计算时,得到特征值Ii≈(A1)ij,i,j=1,2,…,n以及特征向量V。 6)根据特征值从大到小的顺序重新排列矩阵的特征值和特征向量,对复数协方差矩阵的特征值/特征向量进行提取。 自适应阵列天线接收的卫星信号,经累加后得到协方差矩阵进行特征分解,FPGA实现流程图如图1所示。首先将协方差矩阵输入change_rxx2r模块,使得M×M的复数Hermite协方差矩阵转化为2M×2M实矩阵,M为天线阵元数;对于得到的2M×2M的实矩阵,一方面根据第1节中特征求解的步骤2),进行旋转角度的正余弦值求解,另一方面存入ram中实现循环迭代和矩阵元素的读取。接下来,通过M个并行处理器compute实现步骤3),对输入矩阵进行行、列2次角度旋转,然后进入exchange_value模块实现步骤4),完成行、列交换,其中阵元数不同,一次迭代(sweep)交换的次数和规律不同(参考表1)。每次sweep结束后,通过find_max模块寻找新矩阵非对角元素的最大值ξ,进行阈值判断。ξ大于阈值时,将sweep后的新矩阵存入ram中进行下一次sweep迭代运算;ξ小于等于阈值时,矩阵的对角线上元素即为实矩阵特征值。最后,将计算的特征值由大到小排序,去掉重根,根据式(4)得到复数协方差矩阵的特征值,模块sort_self完成该过程实现。 特征向量的实现,依赖于特征值实现过程中得到的正余弦值。当协方差矩阵进入特征分解模块时eig_vector_start=1,特征向量求解开始,初始化特征向量矩阵为2M×2M的单位矩阵。根据第1节步骤3),在eigvector模块中对单位矩阵进行1次角度旋转,将旋转矩阵存入ram中,根据读地址的顺序对旋转矩阵进行行列交换(参考表1)。最后,根据特征值由大到小的排列顺序,将对应特征向量进行排序,并根据式(4)将其转化为复数协方差矩阵对应的特征向量,模块sort_self完成该过程实现。 图1 矩阵特征求解的FPGA实现流程图Fig.1 The flow chart of matrix eigendecomposition FPGA implementation 根据式(10)、式(11)可以看出,矩阵的每次旋转需计算旋转角度的正余弦值,在FPGA实现过程中分别用两种方法进行计算。 CORDIC算法是一系列与运算基数相关的角度不断偏摆,从而逼近所需旋转的角度,可通过该算法进行向量旋转、三角函数、乘、除等运算[11-12]。CORDIC算法分为旋转模式和矢量模式,两种模式的输入输出方式如表2所示,其中X0、Y0、Z0为输入初值。 表2 CORDIC算法两种模式下输出结果 根据式(10)~式(12)所示,在特征求解的过程中需要进行2次旋转模式运算和1次矢量模式运算,在FPGA实现时可通过调用CORDIC IP核来实现矩阵的旋转[13]。 对CORDIC算法实现的特征分解FPGA工程进行仿真分析。仿真设置阵元数为7的阵列天线接收信号,进行单宽带干扰,干扰和信号的功率比为80dB。经计算协方差矩阵的特征分解情况如表3所示。根据对比可以看出,FPGA定点求出的特征值,在小特征值时会有200左右的误差,从而使部分小特征值不能区分重根,影响协方差矩阵特征值和特征向量的提取。 表3 基于COEDIC算法FPGA实现和MATLAB自实现特征值数据比较 进一步对FPGA工程分析可以看出,定点特征分解的误差主要集中在CORDIC核产生的旋转角度θ,由于每次生成θ都会产生误差,随着生成次数和θ的减小,误差会逐渐增大,如图2所示。 图2 旋转角度随旋转次数的变化Fig.2 Variation of rotation angle with rotation times 由于CORDIC核输入/输出数据位宽最大为48bit,精度位宽为48bit。在抗干扰过程中,为了提高抗干扰性能,模拟信号转换为16bit位宽的数字信号,经FPGA处理协方差矩阵数据位宽为18bit。为提高特征分解的精度,需扩大特征分解模块的输入输出位宽,但由于CORDIC核的计算精度为: P=输出位宽+输入位宽+log2(输出位宽) (13) 则特征分解的输入/输出位宽最大可扩到21bit,经FPGA仿真实现的特征值精度较差,不能区分小特征值,如表3所示。若提高特征值分解精度需扩大输入位宽,直接调用CORDIC IP核的实现方法不能满足,可以采用双精度浮点型的方式进行FPGA实现,以满足大位宽、高精度特征分解需求。 根据分析可知调用CORDIC IP核产生的误差是不可避免的,但可以通过对式(12)进一步的推导,实现双精度浮点正余弦值的求解,以避免CORDIC核的使用,从而消除误差。 根据式 (14) (15) 在图1所示的FPGA实现流程中,cos_sin模块通过式(14)、式(15)进行双精度浮点型正余弦值计算,通过实际采集的卫星信号累加计算得到的协方差矩阵进行仿真分析。在实际采集的信号中,单宽带干扰和信号的功率比为80dB,接收七阵元阵列天线,经过双精度浮点特征求解后得到的特征值如表4所示,与MATLAB自实现的特征值完全相同,满足精度要求,表5所示为对应求得的特征向量。 表4 基于双精度浮点FPGA实现和MATLAB自实现特征值数据比较 表5 基于双精度浮点FPGA实现的特征值对应的特征向量 协方差矩阵特征分解一个重要的应用是空间信号DOA估计,对FPGA实现的特征向量可以通过经典DOA估计-多重信号分类(Multiple Signal Classification, MUSIC)进行验证[14]。 MUSIC算法[15]主要是通过寻求阵列空间谱函数PMUSIC的峰值来得到DOA的估计。 (16) 其中,UN为协方差矩阵小特征值对应的特征向量,即噪声子空间;a(θ)为导向矢量。 仿真设置为七阵元阵列天线接收信号,单窄带干扰,干扰与接收信号的功率比值为80dB,干扰的俯仰角设为20°,方位角设为160°。经FPGA进行协方差特征求解的特征值和特征向量进行MUSIC估计,结果如图3所示,估计的俯仰角与方位角与设定值完全相同,基于FPGA实现的特征分解精度符合DOA估计应用。 图3 FPGA实现特征分解DOA估计Fig.3 DOA estimation for FPGA implementation of eigendecomposition 导航抗干扰接收机接收到的信号,其协方差矩阵是复数正定Hermite阵。在特征分解的FPGA实现的过程中,为了简化实现过程,需将复数矩阵转化为实数矩阵。 通过双边Jacobi算法对实数矩阵进行特征值和特征向量的求解,在FPGA设计时,每次旋转角度正余弦的计算误差直接影响实现精度。分别用CORDIC算法和双精度浮点直接计算方法对旋转角度正余弦进行计算,通过对比仿真,CORDIC IP核实现方式具有一定的局限性,适用于处理数据较小矩阵,对于目前使用的导航接收机,信号的协方差矩阵数据为18bit,处理精度不能满足要求。经仿真分析,双精度浮点直接计算方法的FPGA实现满足特征分解精度要求,并通过DOA估计进行应用验证,DOA估计结果正确,满足应用需求。基于FPGA的特征分解实现的方法设计和仿真分析,为导航接收机抗干扰性能的提升提供了有效的工程基础。


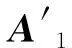
2 特征求解FPGA实现设计

3 仿真分析及应用
3.1 CORDIC算法实现仿真



3.2 双精度浮点实现仿真
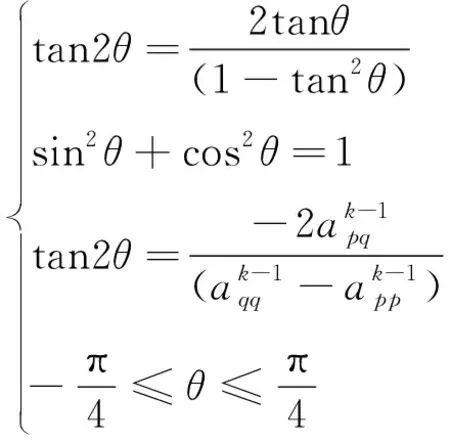




4 结论

