时间模上p-Laplacian方程两点边值问题正解的存在性
2019-09-12 07:29乔世东
山西大同大学学报(自然科学版) 2019年4期
乔世东
(山西大同大学数学与统计学院,山西 大同 037009)
研究时间模T上的一维p-Laplacian两-点边值问题

设p>1,q>1,且满足另外,设

解方程得
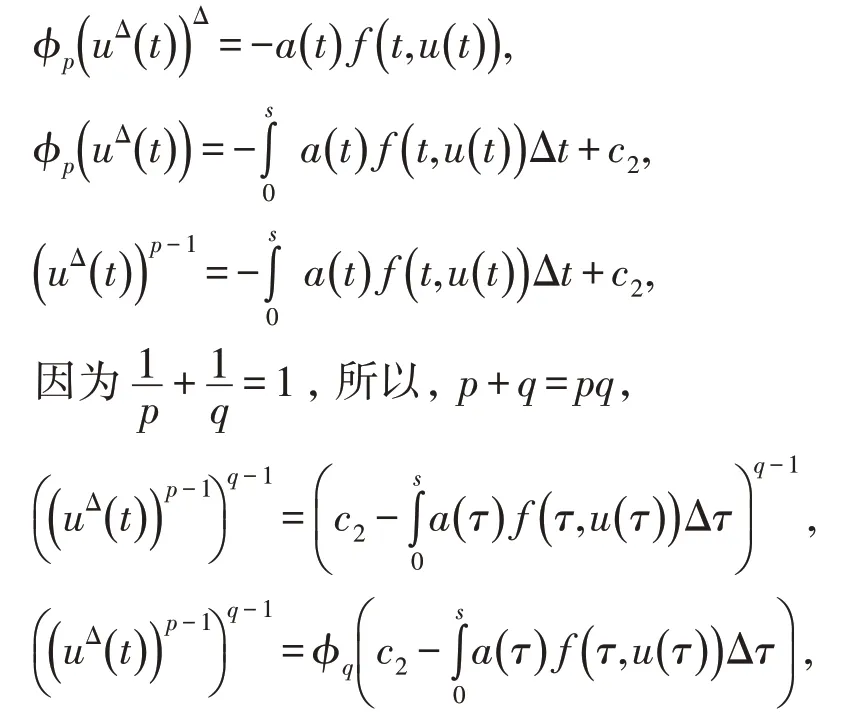
故

亦即


而
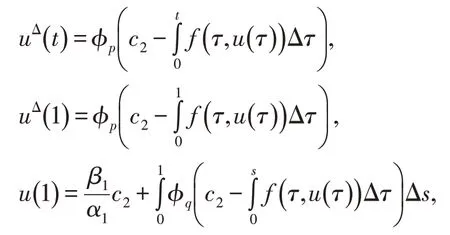
由边值条件得到
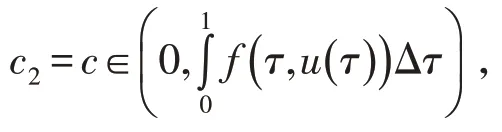
因此


定义全连续积分算子A:P→P,
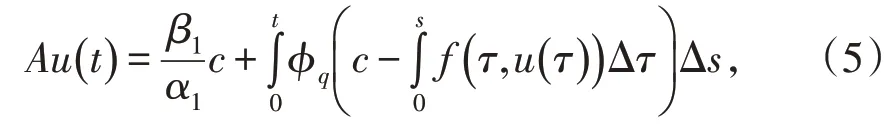
AP⊂P,则A全连续积分算子,令δx∈(0,1),则则(5)为
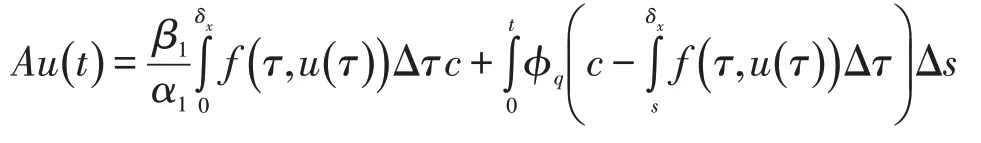
由边值条件得到

所以将A全连续积分算子表示为
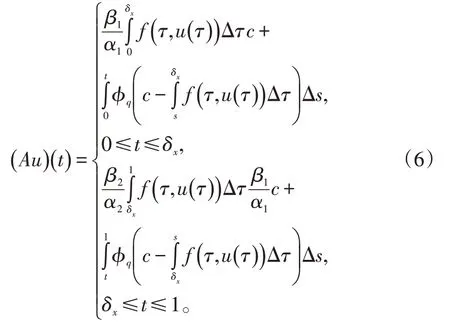
则边值问题(1)有解u=u(t),当且仅当u是对应A在P中的不动点。
引理1设全连续算子由(6)给出,设u∈P,则
‖Au‖=(Au)(δx)。
证明∀t∈(0,δx),
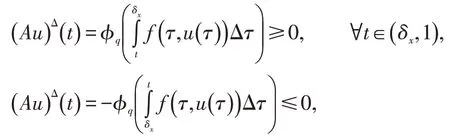
故‖Au‖=(Au)(δx)。[1]
定理1(Krasnoselskii)设E是一个巴拿赫空间,P⊂E是锥,Ω1,Ω2∈E为非空相对开集,且为全连续算子,满足:
(1)‖Au‖≤‖u‖,∀u∈P∩∂Ω1;‖Au‖≥‖u‖,∀u∈P∩∂Ω2,或
(2)‖Au‖≥‖u‖,∀u∈P∩∂Ω2;‖Au‖≤‖u‖,∀u∈P∩∂Ω2,则A在上有一个不动点。[2]
定理2设条件(H)成立,又设存在常数

证明定义一个锥P满足条件(4),引理知AP⊂P,全连续积分算子A:P→P,如果u∈P,‖u‖=a,有

及
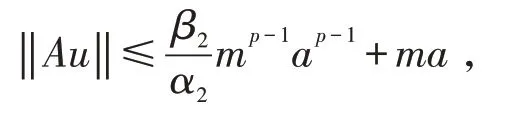
故‖Au‖≤‖u‖。
如果u∈P,‖u‖=b,t∈[δ,1-δ],不妨设有

因此,‖Au‖≥‖u‖,
由定理1知,结论成立。
猜你喜欢
东北师大学报(自然科学版)(2022年4期)2023-01-16
数学物理学报(2022年5期)2022-10-09
数学物理学报(2022年4期)2022-08-22
数学物理学报(2022年1期)2022-03-16
数学物理学报(2021年5期)2021-11-19
安阳师范学院学报(2021年5期)2021-11-08
数学物理学报(2021年2期)2021-06-09
数学物理学报(2021年1期)2021-03-29
山西大同大学学报(自然科学版)(2020年3期)2020-07-17
中等数学(2019年12期)2019-05-21

