刘岳云《测圆海镜通释》补证与解读
李兆华
(天津师范大学数学科学学院,天津 300387)
据李冶(1192~1279)《测圆海镜》(1248)可知,勾股测圆术包括圆城图式、识别杂记与10个容圆公式、已知2事求得圆径(主要采用天元术建立方程的方法)等三部分内容。第三部分已臻完善,而前两部分尚有明显的不足。此不足之处,遂成为晚清算家研究之重点。
19世纪70年代至20世纪初,《测圆海镜》的研究是一个活跃的课题,三十余年间成书十余种。[1]其中,李善兰(1811~1882)、刘岳云(1849~1917)、王季同(1875~1948)[2]等均有深刻的工作面世。李善兰于同治七年(1868)任教同文馆直至去世,其间曾传授《测圆海镜》,并以该书内容命题考试,且将部分试题与解答收入《算学课艺》(1880)以广传播。又为同文馆集珍版《测圆海镜》作序(1876)以表彰其成就。所著《九容图表》(不分卷),后来收入《古今算学丛书》(1898)。《九容图表》将圆城图式予以增删并确定为十三率勾股形。相应地,将识别杂记中的有关内容予以增删且编为十三率勾股形等量表。[3]虽然传本《九容图表》遗议尚多,但是李善兰的研究与教学成果以及“合中西为一法”[4]的教学思想,对此期《测圆海镜》的研究具有重要影响。刘岳云《测圆海镜通释》(1896)4卷与王季同《九容公式》(不分卷,1898)各有所长而意向不同。王季同意在运用汉译代数符号简化勾股测圆术的圆径算法[5],刘岳云则将识别杂记有关的内容“分别条理,为立数表”以构建勾股测圆术的理论并用于求解圆径。李善兰与刘岳云关于“九容”问题主张不同,刘岳云之名因之多次见于有关论述中。然而,《测圆海镜通释》迄无专题的讨论,此即本文之关注所在。
因稿本遗失,刘岳云仅以“残帙”付梓,即今传《测圆海镜通释》4卷,光绪二十二年(1896)成都尊经书局刊本。(1)高红成博士代为查阅北京大学图书馆藏民国元年存古书局本。据两书的版式、字体、图式、误文对勘,知存古书局本正文系据尊经书局本原版重印。李迪《中国算学书目汇编》记有“民国元年(1912年)四川存古堂刊本一册(四川,重)”,疑即存古书局本。刘岳云认为是本“大略已具”,故尚可据以了解其主要工作。因该书内容有所缺失及文字脱误,故本文就其要点予以补证,文字脱误凡有关算理者一并校改,并就其难点予以分析和说明,以期较为准确地阐明其“比例之理,相等之数”的意义与运用,并藉以了解勾股测圆术在晚清的发展与变化。
1 成书过程与内容梗概
刘岳云,字佛卿,江苏宝应(今属扬州市)人。光绪十二年(1886)进士,历官户部主事等。[6]光绪三年(1877)“于金陵算学书局教习生徒”。[7]光绪二十二年(1896)主讲成都尊经书院。[8]刘岳云与李善兰、吴嘉善(1820~1885)[9]均有学术交往。“二十岁(1868),至金陵谒李壬叔(善兰)先生、吴子登(嘉善)先生,遂得并通代数。”[10]光绪六年(1880)李善兰将当年出版的《算学课艺》一部赠刘岳云。([10],光绪六年条)稍后,刘岳云将所著的《格物中法》书稿寄示李善兰。[11]《格物中法》载曾纪泽(1839~1890)识语称,“君为吴子登编修高第弟子,宜其精深博大也。”[12]刘岳云的数学著述不少,但付印者不多。除《测圆海镜通释》外,尚有《算学丛话》(不分卷,1896)、《喻利算法》(不分卷,1896)及《五经算术疏义》(1899)2卷。(2)李俨《近代中算著述记》载:“《课徒算草》二卷。刘岳云撰,已刻(北)”。经查未见。关于刘岳云与西学中源说,近年已有评述,可以参考。[13]
今传本《测圆海镜通释》4卷是一个残帙。自原稿初成、遗失以致残帙刻成,先后经历二十余年。以下两段引文清楚地记述了这一过程:
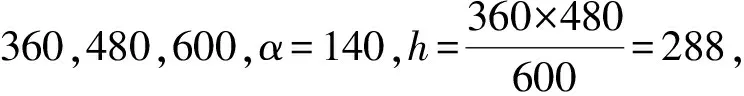
辛巳年,家叔俛兄以稿寄四川学使朱君肯夫,许为代刻。会肯夫卒于学使任,书未及刻。癸未年,叔俛兄亦卒,遂无从询颠末。儿子启瑞于旧稿中搜得残帙,略分四卷,写一清本。余心气不逮曩时,不能补为之。顷主讲成都尊经书院,冯生书以第四卷重为排比算校,并前三卷交院中梓人刻成。[8]
据此可知以下三点:(1)原稿本成于同治甲戌(1874),光绪辛巳(1881)定稿并寄出付刻,不意丢失。光绪二十二年将残帙略作整理刻于尊经书院。(2)定稿寄出之前,于光绪丁丑(1877)见到李善兰“有大中垂线、明勾股和求城径一题,因又以垂线、方边配合各勾股率,增二卷”。查尊经书局本并无所增内容。定稿寄出之前一年,收到李善兰所赠之《算学课艺》,并指出“其和勾股、断勾股即余之高平和、高平较。”是知刘岳云见到《算学课艺》之时,高平和、高平较二形已先有定名。(3)至于陈维祺“海镜二表”,有证据表明,受到李善兰《九容图表》的影响。[3]谓之“全同余说而稍变其面目”,似属过当。故《测圆海镜通释》4卷的内容当为刘岳云独立的工作,且1881年可视为工作完成的时间。
该书的内容梗概如下:
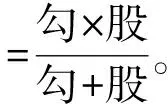
卷2,边股,共12题,有边股与另形的1事求圆径。《测圆海镜》卷3边股,原17题。将第9题、第14题并入第1题,第6题并入第5题,第16题并入第11题,第8题归入通弦类移入卷4。共得12题成卷。
卷3,通股,共16题,有通股与另形的1事求圆径(第15题另事为明股叀勾和)。《测圆海镜》卷5大(通)股,原18题。将第11题并入第8题,第12题并入第9题。共得16题成卷。
卷4,通弦,共25题,有通弦与另形的1事求圆径(第23题另事为全径虚弦和,第24题另事为边勾底股和)。本卷第1题至第20题为新增(第13题由《测圆海镜》卷3第8题移入)。第21题至第24题、第25题分别为《测圆海镜》卷9上大(通)斜第1题至第4题,卷11杂糅第16题(卷12之分第7题、第8题以“书旨不同故未及”)。共得25题成卷。
卷2至卷4共53题。其中,卷4的内容比较详细,每题之下分列“释曰”、“术曰”和“草曰”三项。
书名所谓通释并非《测圆海镜》的逐题疏解,而以识别杂记为之重点。《算学丛话》载:
识别杂记约五百条,多未经审定。故于大小勾股所以比例及相等之故,仍未能融会贯通。李四香意在阐立天元,故于比例及相等之故亦未及核。余读此书时,取杂记分别条理、为立数表,然后比例及相等之故洞然明白。于是,不循敬斋次第,别为一书,名之曰《测圆海镜通释》,专明大小勾股比例[及相等](8)此处疑脱“及相等”三字,“比例及相等之故”上文凡三见。据补。之理。([7],1b)
其门人冯书的跋文称:
细绎先生各表,始于其中比例之理、相等之数,靡弗用之吻合。([8],1a)
门人杨骏跋文亦称:
丙申岁,宝应先生主讲尊经书院及读先生书,穷究一月,颇能贯通等数、比例之理。([8],2a)
显然,刘岳云之目的在于求故明理。对照该书内容可知,“比例”即相似勾股形的比例式,“等数”即十三率勾股形169事的等量关系及勾股恒等式(20个)。“比例之理、相等之数”是勾股测圆术的理论概括。比例无须详述,而等数则由“分别条理、为立数表”之诸率差等表与勾股相乘等数表给出。
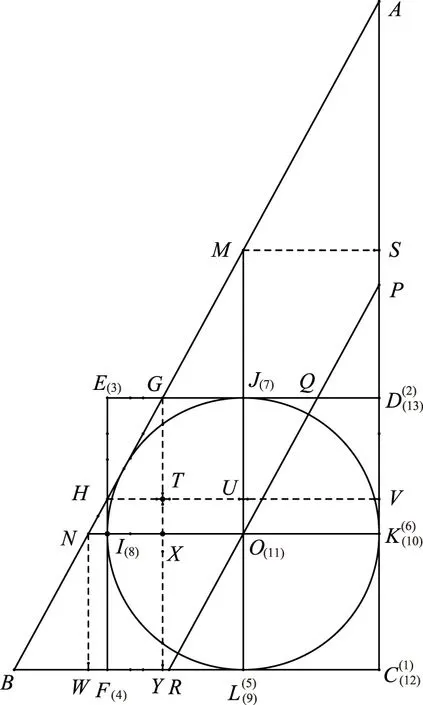
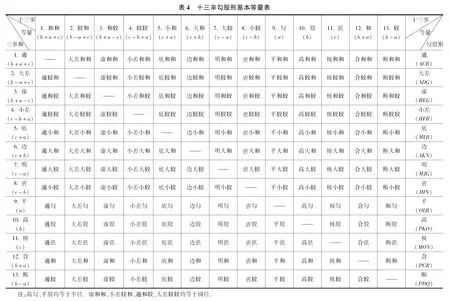
图1 《测圆海镜通释》图式
2 《测圆海镜通释》图式
在圆城图式中,刘岳云添加过圆心且与弦平行的线段PR,如图1所示。此线原为虚线,今改实线。4条虚线原为实线。线段交点原用汉字表示,今改字母。各直角顶点右侧的数字表示十三率勾股形在本文的序号。圆城图式原有16个勾股形。下高RtΔMUH、上平RtΔGXN、虚RtΔGTH分别有全等形RtΔASM、RtΔNWB、RtΔHEG。又,黄广RtΔAVH、黄长RtΔGYB分别有边长减半形RtΔASM、RtΔNWB。将RtΔMUH及RtΔAVH等5个勾股形删去。将上高RtΔASM、下平RtΔNWB分别平移至RtΔPKO、RtΔOLR。共得11个勾股形。增加高平和RtΔPCR、高平较RtΔPDQ。共得13个勾股形。此即刘岳云的十三率勾股形。高平和形、高平较形,李善兰分别称之为合勾股形、断勾股形。本文皆以合、断名之以求简便。十三率勾股形与圆的位置关系如表1所示:
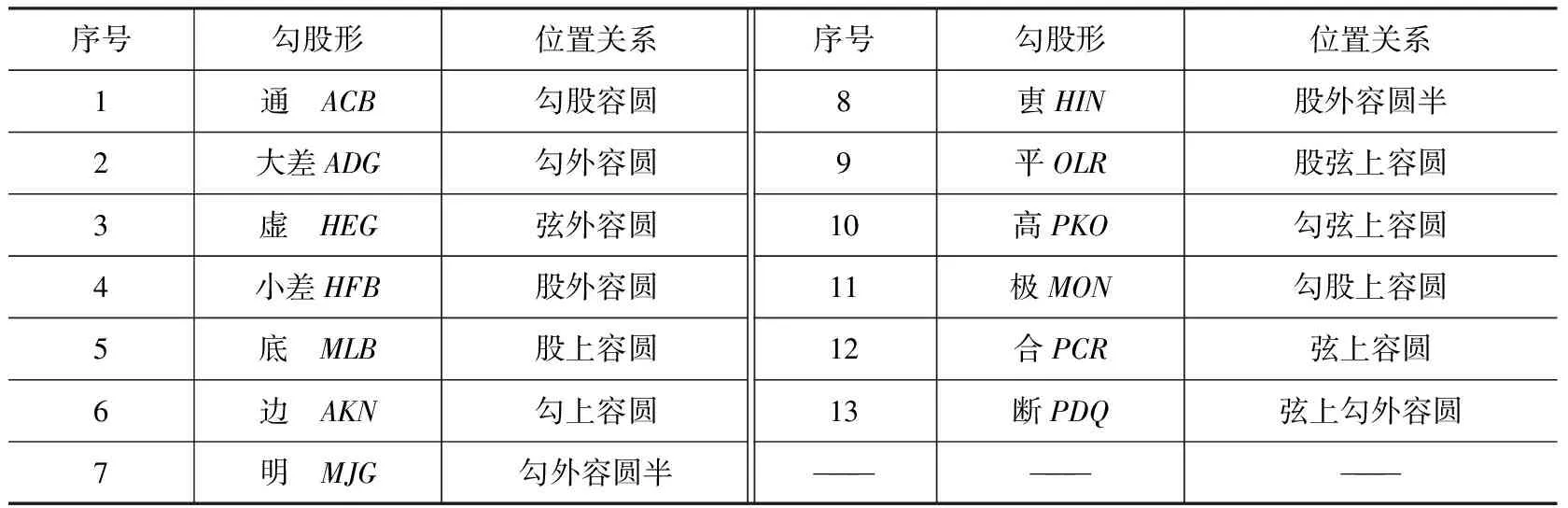
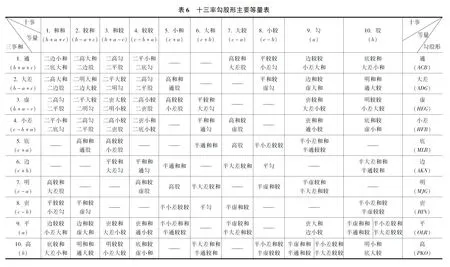
表1 十三率勾股形与圆的位置关系1)
1) 平形、高形与圆的位置关系依极形之例补。断形与圆的位置关系依参考文献[15]补。其他均依刘岳云勾股九容表及副表。
十三率勾股形的确定使“九容”发展为“十三容”,勾股测圆术的内容随之形成系统。十三率勾股形具有如下的性质:(1)十三率勾股形均相似;(2)十三率勾股形的和和与通形的13事一一对应相等;(3)由十三率勾股形的任一形求圆径皆倍其勾股相乘积除以本形定率。后两个性质详见本文第4节、第7节。
3 诸率差等表与勾股相乘等数表
识别杂记的研究需要解决两个问题:(1)勾股形等量关系之确定。(2)圆径幂公式(包括半段径幂公式、半径幂公式)及各率勾股形的圆径公式由来之解释。
每个勾股形有13事,十三率勾股形共169事。在169事中,存在2事相等、1事等于另1事2倍的情形。显然,若所给2事相等或为倍半则不能据以求得圆径。若作等量代换运算则需确知2事相等或为倍半。169事,必先厘清其等量关系,而后始可付诸应用。又由十三率勾股形的圆径公式以及圆径幂公式的结构可以概括出,已知满足条件的2事,运用有限次五则运算(加、减、乘、除、开平方)可以表示圆径。据此可以回答“勾股测圆术是什么”这一问题,而诸式的依据并不清楚。解释其由来即以阐明其依据,俾有所取信。以上两个问题之解决,皆赖本节标题所指二表之应用。
诸率差等表,如表2所示。原表横行,今改竖列。原表黄广形、黄长形今删。表2的左半与右半结构相同。兹以左半为例说明其意义。通形由底形与高形构成,高形由虚形与明形构成,底形由小差形与高形构成(亦由平形与极形构成),小差形由平形与叀形构成,平形由叀形与虚形构成。对照图1,显然正确。再考虑到表2的右半,可得:
平=叀+虚
极=叀+虚+明
边=叀+2虚+2明 高 =虚+明
大差=虚+2明
通 =2叀+3虚+2明 小差=2叀+虚
底 =2叀+2虚+明
此外,
合=高+平=叀+2虚+明 断=高-平=明-叀
表2 诸率差等表
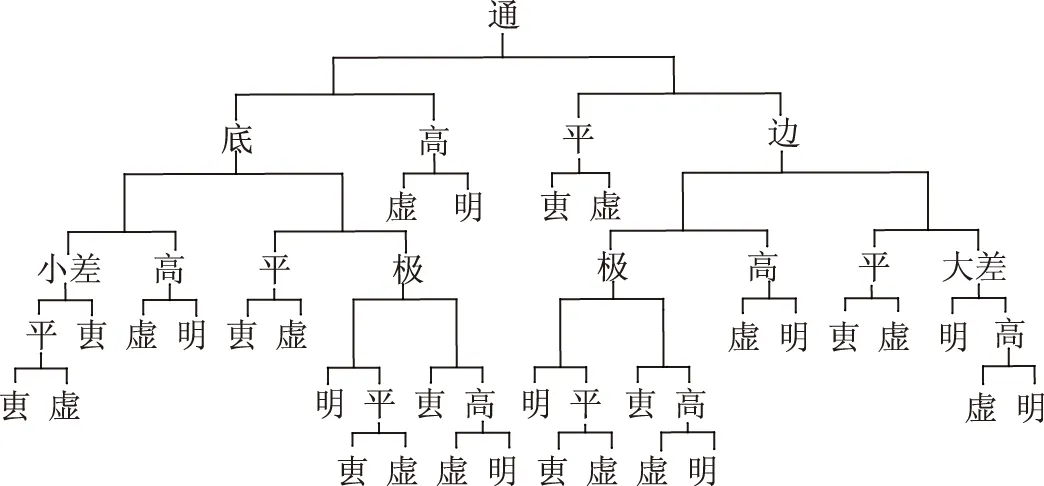
由此可知,在十三率勾股形中,叀形、虚形、明形可以作为基本的3形表示其他10形。上述各式稍显复杂,不便入算,可简化如下。由

因而,亦可用极形、高形、平形表示其他10形:
通 =高+平+极
小差=极-高+平
明 =极-平
断 =高-平 大差=高-平+极
底 =极+平
叀 =极-高
虚=高+平-极
边=极+高
合=高+平
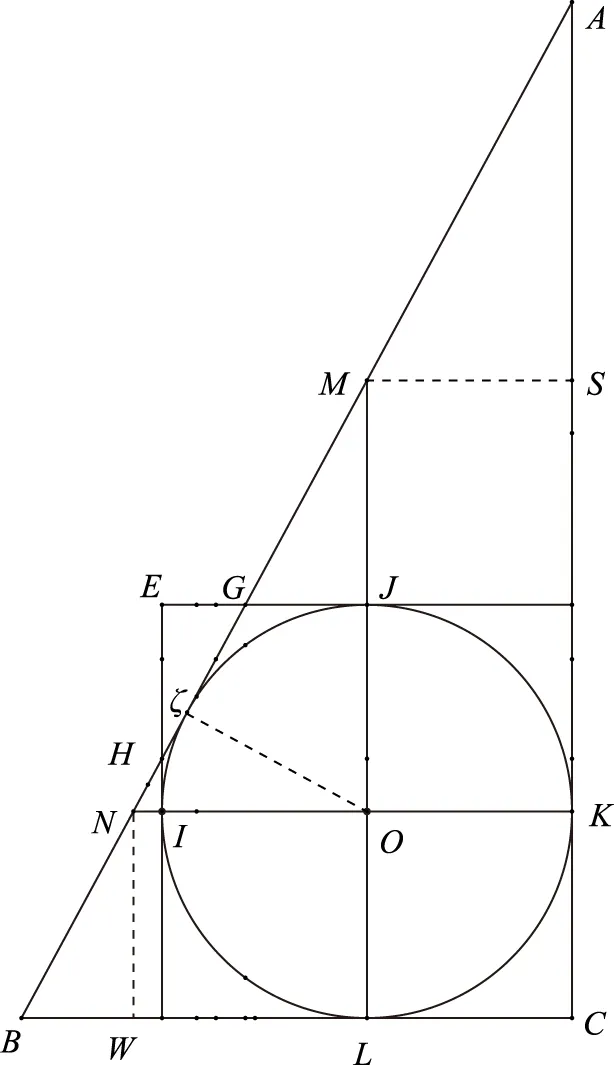
图2 极高平的关系
以上10式对勾、股、弦均成立。例如:
通勾=高勾+平勾+极勾
通股=高股+平股+极股
通弦=高弦+平弦+极弦
由识别杂记又可知,极形、高形、平形的勾、股、弦之间的关系:
极弦=高股+平勾(“极弦乃高股平勾共”。识别杂记,诸弦)
高弦=极股(“日之于心与日之于山同”。识别杂记,诸杂名目)
平弦=极勾(“川之于心与川之于月同”。同上)
高勾=平股(均等于半径)
如图2,过切点作半径Oζ(刘岳云称之为极垂线)。RtΔMON、RtΔMζO、RtΔOζN分别是极形,高形,平形。上列4式显然成立。
以上关于极形、高形、平形的14个等式用于计算169事的等量关系。
勾股相乘等数表,即勾股恒等式表,如表3所示。(9)本表与勾股十三事加减表始见于吴嘉善《算书二十一种·勾股》,同治二年(1863)自序,白芙堂算学丛书本。刘氏此二表当出于此。原表竖列,今改横行。原表“大差”和“二小差”,“差”字均改作“较”以与13事名称一致。设通形的三边分别为a、b、c。其中,a 表3 勾股相乘等数表 和较×和和=较较×较和 可由 二勾×股=和较×和和 二勾×股=较较×较和 导出,亦删去之,共余20式。为了下文讨论之便,兹将20个勾股恒等式的顺序稍作调整,排列如下: (1)勾×和和=大和×较较 (3)勾×和较=小较×较和 (5)二勾×小和=较较×和和 (7)股×和和=小和×较和 (9)股×和较=大较×较较 (11)二股×大和=较和×和和 (13)二股×勾=和较×和和 (15)和和2=二大和×小和 (17)和较2=二小较×大较 (19)勾2=小较×大和 (2)勾×较和=大和×和较 (4)勾×较较=小较×和和 (6)二勾×大较=和较×较和 (8)股×较和=大较×和和 (10)股×较较=小和×和较 (12)二股×小较=较较×和较 (14)二股×勾=较较×较和 (16)较和2=二大较×大和 (18)较较2=二小较×小和 (20)股2=大较×小和 以上20个勾股恒等式对十三率勾股形的任一形均成立,下文不止一次运用之。 等量关系可以分为基本的与主要的两类。诸率等数表(12)删去黄广形、黄长形及明叀和形。给出十三率勾股形的基本等量关系,《算学丛话》又概括为如下的规律: 通、边、底、大差、小差、高、平(倍高即广、倍平即长、故不数)(13)括号内文字系原文的双行夹注。下同。、极、虚、明、叀、合、断(即高平和、高平较二率),凡十三率。通得各率之和和,边得各率之大和,底得各率之小和,大差得各率之较和,小差得各率之较较,高得各率之股,平得各率之勾,极得各率之弦,虚得各率之和较,明得各率之大较,叀得各率之小较,合得各率之和,断得各率之较,互为比例。故不增高平和、高平较二率,其理不备也。 诸率等数表及以上的规律,初读不得其详。为了准确理解,兹将该表内容逐项写出,如表4。在表4中,十三率勾股形的顺序有所调整以与表1一致,而规律不变。例如,“通得各率之和和”,即十三率勾股形的和和与通形的13事一一对应相等。“边得各率之大和”即十三率勾股形的大和(股弦和)与边形的13事一一对应相等。 由表4可见,左上至右下对角线上共13事,每格内均标注短线,表示该事无等量(自身相等)。此13事,晚清支宝枬(1854~1912)称之为本形定率。[16]例如,通形的定率是和和,大差形的定率是较和。对角线下方78事,每事的等量写在相应的格内,共得78个等量关系,本文称之为基本等量关系。对角线上方的78个等量关系与下方的78个一一对应相同。兹以大差和和为例说明其计算过程,其他各事仿此可得: 大差和和=通较和 大差和和=大差股+大差勾+大差弦 =高股-平股+极股 (大差=高-平+极) +高勾-平勾+极勾 +高弦-平弦+极弦 =高股-高勾+高弦 (高勾=平股 +平股-平勾+平弦 高弦=极股 +极股-极勾+极弦 平弦=极勾) =通股-通勾+通弦 (高+平+极=通) =通较和 此即大差和和与通较和两格的内容。 除基本等量关系外,《测圆海镜通释》还用到不见于表4的另一些等量关系。例如,卷4第20题, 通和和=2边小和 此外,卷2第8题、第12题,卷3第2题、第7题,卷4第1题、第14题、第17题、第18题等等均有其例。此类等量关系,刘岳云曾否集中列于卷1,今不得知。 此类等量关系本文称之为主要等量关系,共有20个。其原始记载散见于识别杂记各节。运用基本等量关系的算法,并注意到 极弦=高股+平勾 即可求得之,其规律随之可见。由表4可知,只需计算对角线下方的78事即可。显然,除极形、高形、平形外,合形与断形均不含极弦亦无需考虑。故只需对其余7形施以上述代换。兹将计算结果列为表5。在表5中,凡格内标注短线者,表示该事的等量与表4的结果相同,视为在本表无等量。粗实线弦折形内共28事。其中8事无等量,余20事有之,计有20个等量关系。弦折形外共27事。其中8事无等量,余19事有之,而高勾有等量2事,亦有20个等量关系。弦折形内外各有20个主要等量关系且一一对应相同。表4对 角线下方78事各有等量1事,而其中的20事还有另1事,故此20个等量关系称为“主要的”,以示区别。兹仍以大差和和为例说明之,其他各事仿此可得: 高大和在表5对角线下方,取2高大和入表。此即大差和和与高大和两格的内容。边股在对角线上方,2边股暂不入表。 如前所述,弦折形内外各有20个主要等量关系且一一对应相同。弦折形之外的20个分布在平形一行上6个,高形一行上8个,对角线上6个。为了讨论之便,以此为序将20个主要等量关系逐一写出(系数有半者化整),即 (1)平和和=边较较 (2)平较和=边和较 (3)平和较=叀较和 (4)平较较=叀和和 (5)二平小和=小差和和 (6)二平大较=虚较和 (7)高和和=底较和 (8)高较和=明和和 (9)高和较=明较较 (10)高较较=底和较 (11)二高大和=大差和和 (12)二高小较=小差和较 (13)二高勾=虚和和 (14)二高勾=小差较和 (15)通和和=二边小和 (16)大差较和=二明大和 (17)虚和较=二叀大较 (18)小差较较=二叀小和 (19)平勾=叀大和 (20)高股=明小和 为了运用的方便,表5需做两点补充。(1)在各格所记的1事之下,依表4补入该事之等量。例如,大差和和格记有二高大和,其下补二边股。而边小和格记有半通和和,其下无可补。通和和为本形定率,无等量(自身相等)。此种情形共有6格。将对角线上及其下方当补者如法补足。(2)将对角线下方各格内容补入上方相应各格。例如,大差和和格之二高大和、二边股补入通较和格。凡在表5无等量者仍标注短线。补充的结果形成表6。 表4与表6统称为“十三率勾股形等量表”,两表可合并写成一表,兹从略。合并后的表与李善兰“十三率勾股形等量表”([3],47页)比较:虚和和,小差较和,通和较,大差较较,高勾,平股等6格有所不同。李善兰表后原有补识:“大和较,大差较较,虚和和,小差较和均等圆径。平股,高勾均等半径。”据此,将李善兰表上述6格内容稍作改动则两表全同。 表4对角线上及对角线下方共13+78=91事。表5弦折形内有等量的共20事(亦即20个主要等量关系等号右端的20事),相减,得71事,即所谓独立的71事([5],709页)。再减去表4对角线下方等于半径的高勾,共余70事。此70事无彼此相等、倍半及等于半径者,任取其中2事作为已知条件可得圆径。 20个主要等量关系是20个勾股恒等式在十三率勾股形中的表现形式,其原因是两者可以变换。 主要等量关系变为勾股恒等式。为了简便,引入泛积的概念。设通形的第i事为pi,和和为p1,第j率勾股形的第i事为pji,和和为pj。因十三率勾股形均相似,故 晚清陈维祺称pjpi是pji的泛积[17],i,j=1,2,,13。因十三率勾股形的和和与通形的13事一一对应相等,故pj亦即通形的第j事。据此,由通形的勾、股、弦即可求得十三率勾股形169事的泛积。一如上文,通形的三边分别为a、b、c,将20个主要等量关系依次写成泛积式如下: (1)a(b+a+c)=(c+b)(c-b+a) (2)a(b-a+c)=(c+b)(b+a-c) (3)a(b+a-c)=(c-b)(b-a+c) (4)a(c-b+a)=(c-b)(b+a+c) (5)2a(c+a)=(c-b+a)(b+a+c) (6)2a(c-a)=(b+a-c)(b-a+c) (7)b(b+a+c)=(c+a)(b-a+c) (8)b(b-a+c)=(c-a)(b+a+c) (9)b(b+a-c)=(c-a)(c-b+a) (10)b(c-b+a)=(c+a)(b+a-c) (11)2b(c+b)=(b-a+c)(b+a+c) (12)2b(c-b)=(c-b+a)(b+a-c) (13)2ba=(b+a-c)(b+a+c) (14)2ba=(c-b+a)(b-a+c) (15)(b+a+c)2=2(c+b)(c+a) (16)(b-a+c)2=2(c-a)(c+b) (17)(b+a-c)2=2(c-b)(c-a) (18)(c-b+a)2=2(c-b)(c+a) (19)a2=(c-b)(c+b) (20)b2=(c-a)(c+a) 又将表3的20个勾股恒等式写成字母表达式,所得与上列20个泛积式一一相同。以上说明“系”可变为“式”。 勾股恒等式变为主要等量关系。兹以勾股恒等式(1)导出主要等量关系(1)为例说明之。仿此,其他各式依次可得: 式(1) 勾×和和=大和×较较 A.平形的定率是勾。在平形中,由式(1)有 即 平和和=边较较 (A1) 又 即 平和和=小差大和 (A2) B. 通形的定率是和和。在通形中,由式(1)有 即 通勾=边较较 (B1) 又 通勾=小差大和 (B2) C.边形的定率是大和。在边形中,由式(1)有 即 边较较=平和和 (C1) 又 边较较=通勾 (C2) D.小差形的定率是较较。在小差形中,由式(1)有 即 小差大和=平和和 (D1) 又 小差大和=通勾 (D2) 在上列各步中,(B)、(C)、(D)的步骤有省略,参见(A)自明。在上列8个等量关系中,(A1)、(C1)即表5平和和与边较较2格的内容,(A1)即主要等量关系(1)。以上说明“式”可变为“系”。 上列8个等量关系即表6平和和,边较较,通勾,小差大和4格的内容。这一推导方法可用于检验表6的正确性。 由十三率勾股形的等量关系可以导出以下4个常用的辅助关系: 因 高股=明小和=明弦+明勾,又由图2, 高股=明弦+Gζ 故 明勾=Gζ 因 平勾=叀大和=叀弦+叀股,又由图2, 平勾=叀弦+Hζ 故 叀股=Hζ 因 边股=高大和=高弦+高股,又由图2, 高弦+高股=Aζ 故 边股=Aζ 因 底勾=平小和=平弦+平勾,又由图2, 平弦+平勾=Bζ 故 底勾=Bζ 以上4式即今之切线长定理,运用该定理可减少代换使运算简化。虚和和、小差较和、通和较、大差较较均等于圆径的证明即其一例。字母表示的4个量不在169事之内,可视为辅助量。 在命题证明、方程建立过程中,等量代换是常用的方法。兹以不在同一勾股形的2事加减为例说明之。以下各例选自识别杂记,运算过程系本文所加。 识别杂记的个别条目或自注包含等量代换的提示,《测圆海镜》四库馆按亦有个别提示。虽为数极少,但给出命题证明的方向。 勾股九容表及副表、圆径幂等数表分别给出十三率勾股形的圆径公式与圆径幂公式。副表为刘岳云新增,包括高、平、合、断的圆径公式。其他各式出自《测圆海镜》卷2与识别杂记内诸杂名目节。《测圆海镜》约有半数的题目依上述公式建立方程,而公式的由来并未明示。《测圆海镜通释》有所提示。兹据勾股恒等式,并注意到高勾、平股均等于半径,虚和和、小差较和、通和较、大差较较均等于圆径,试为推导。 以下推导圆径公式,十三率勾股形顺序依表4。 勾股恒等式(13) 2股×勾=和较×和和 对于十三率勾股形均成立。又,通和较、虚和和均等于圆径,任取其一,此取通和较。 在通形中,有 2通股×通勾=通和较×通和和, 即 在大差形中,有 即 在虚形中,有 即 在小差形中,有 即 依序继续进行,直至在断形中,有 即 由此可归纳得 此即十三率勾股形的圆径公式。各式的等量代换及本形定率参见表4。 由勾股恒等式(14),又,大差较较、小差较和均等于圆径,任取其一,可得同样的结果。 以下推导半段径幂公式: 勾股恒等式(17) 和较2=2小较×大较 在通形中,有 通和较2=2通小较×通大较,通和较=径, 即 此即前式。由勾股恒等式(15),在虚形中可得同样的结果。 勾股恒等式(18) 较较2=2小较×小和 在大差形中,有 大差较较2=2大差小较×大差小和,大差较较=径, 即 此即后式。由勾股恒等式(16),在小差形中可得同样的结果。 以下推导半径幂公式: 半径2=叀股×边股 半径2=明勾×底勾 半径2=高股×平勾 半径2=明小和×叀大和=明大和×叀小和 勾股恒等式(19) 勾2=小较×大和 在高形中,有 高勾2=高小较×高大和,高勾=半径, 即 勾股恒等式(20) 股2=大较×小和 在平形中,有 平股2=平大较×平小和,平股=半径, 即 以上为前2式。又, 以上为后2式。圆径幂公式计有6式,各式的等量代换参见表4和表6。 由勾股定理,弦可由勾、股表出,故以上诸式皆以2事并五则运算表示圆径,且皆可由勾股恒等式导出。勾股恒等式原为求解与构造勾股形的公式,今用以求解圆径。可见,勾股恒等式是勾股和较术与勾股测圆术共同的理论依据。 晚清算家已注意到圆径公式与圆径幂公式的证明([1],第3节、第4节)。然而,或证前者,或证后者,且方法各异。运用勾股恒等式可使证法划一且较简单。由本文下节可见刘岳云运用这一方法的例子,虽仅有两例,但可得到提示。 尊经书局本刊刻不精。存古书局重印本亦未校改。今依校算,就术与草的文字错漏予以校改。凡校改的文字用方括号标出,随文说明理由。算式亦有个别符号、系数错误,依草演算不难改正。以下仅注明“算式有误”,具体算式从略。 (1)卷2第10题 边股、明弦求圆径。 第一法演草:“另以,又与高较和[幂]相乘得为同数。” 按:“幂”,原文误夺。同数当为 (2边股×半径+高较和2)×高较和2 依算校补。算式有误。 (2)卷2第12题 边股、叀小和求圆径。 第一法演草:“为小差大较,[与小差大和]相乘得为半段径幂。寄左。” 按:“与小差大和”凡五字,原文误夺。由勾股恒等式(16)知, 小差较和2=2小差大较×小差大和 而小差较和即圆径,故小差大较当与小差大和相乘为半段径幂。上文已求得小差股、小差弦,相加即得小差大和。依算校补。算式有误。 (3)卷3第15题 通股、明股叀勾和求圆径。 第三法演草:“立天元一为半径,,置通股,以天元减之得为[半通较和]。以二之天元乘之得,合以通大较除之为通勾。” 按:“半通较和”,原文误作“倍通黄”。通股减天元半径等于边股,而倍通黄即四半径,两者无必等之理。通较和等于倍边股,故通股减天元半径与半通较和等。由勾股恒等式(6)知, 又,通和较即圆径,亦即二之天元。以二之天元乘半通较和,除以通大较得通勾,与末句恰符。依算校改。 (4)卷4第2题 通弦、明和求圆径。 演草:“另于全径加倍通弦得为通和和,与[倍]明和相乘得,内减通弦幂,又加四之半径幂得,自之得,为同数。” 按:“倍”,原文误夺。同数当为 (通和和×2明和-通弦2+4半径2)2 依算校补。 (5)卷4第6题 通弦、大差较求圆径。 术文:“四为[负]隅。开立方得半径。” 按:“负”,原文误作“正”。若为正隅,方程其他各项当正负易号。依算校改。算式有误。 (6)卷4第7题 通弦、大差和求圆径。 演草:“为全径。加通弦得为通和。[再加通弦为通和和。通和]自之得为通和幂。” 按:“再加通弦为通和和。通和”凡十字,原文无之。演草下文需用通和和、通和幂入算。依意校补。 又,演草:“为通弦乘通和于上,又以通和[和]乘大差和得下式,以减上得,自之得,为同数。” 按:下一“和”字,原文误夺。同数当为 (通弦×通和-通和和×大差和)2 依算校补。算式有误。 (7)卷4第9题 通弦、高小较求圆径。 演草:“为高较较。以半径乘之得下式为高和和[乘高小较]幂。” 按:“乘高小较”凡四字,原文误夺。由勾股恒等式(4)知, 高勾×高较较=高小较×高和和 又,高勾即半径。故高和和须与高小较相乘方与下式等。依算校补。 (8)卷4第11题 通弦、高和求圆径。 术文:“通弦减倍高和,自乘[于上,高和自乘倍之,以减上],为正从。” 按:“于上,高和自乘倍之,以减上”凡十一字,原文误夺。正从当为 (通弦-2高和)2-2高和2 依算校补。 (9)卷4第12题 通弦、高平和之和(14)高平和之和即合勾股形之勾股和,亦即合和。求圆径。 术文:“倍通弦与[高平和之和]相减,[倍之]为正从。” 按:“高平和之和”,“高”上原衍一“倍”字,今删。“倍之”二字,原文误夺。正从当为 2(2通弦-合和) 依算校改。 (10)卷4第16题 通弦、边较和求圆径。 演草:“为通和和,加边较和得,自之得,通[较]幂乘之得为如积。” 按:“较”,原文误作“弦”。如积当为 (通和和+边较和)2×通较2 依算校改。 (11)卷4第22题 通弦、通较求圆径。 演草:“为倍通小较,加倍通较得为倍通大较,与倍通小较相乘得为[两]段径幂,为如积。” 按:“两”,原文误作“半”。由勾股恒等式(17)知, 通和较2=2通小较×通大较 又,通和较即圆径。上式两端各倍之,得两段径幂。依算校改。 《测圆海镜通释》卷4前20题,除第13题外,为刘岳云新增。诸题体现了刘岳云建立圆径方程的方法。每题均立天元为半径,计算如积、同数,两式相消得方程。此系天元术常法,无需赘言。其法之难点在于寻求相等的如积与同数。此式为建立方程的依据,而各题均未说明其由来。本文以“比例之理、相等之数”为据,将其中比较典型的如积同数式予以补证以求其立术之由。如积同数式所需各项,散见于原文之“释曰”与“草曰”之内。兹稍加整理、补充,统一置于各式之前。方程均以《测圆海镜》卷1今问正数验证之。 (1)卷4第5题 通弦、虚小较求圆径。 记通弦=α,虚小较=β,半径=x,则 虚和和=径=2x, 通和=通弦+径=α+2x 通和和=2通弦+径=2α+2x,通较2=2通弦2-通和2=2α2-(α+2x)2 如积同数式 半径2×通较2=(通弦×半径-2半径2-虚小较×通和和)2 方程 2x4+2βx3+β(α+β)x2-αβ(α-2β)x+α2β2=0 依今问正数,α=680 ,β=12,代入,求得x=120。 将如积同数式两端开平方,移项,整理, 即 虚小较×通和和=虚和和×通小较 此式显然成立。且虚和和,通和和及虚小较已由α,β,x表出,只需将通小较表出。逆推即得。 (2)卷4第9题 通弦、高小较求圆径。 记通弦=α,高小较=β,半径=x,则 通和较=2高勾=径=2x ,高和较=高勾-高小较=x-β 如积同数式 高勾×(高勾×高较较-高勾×高小较+高小较2)=通弦×高和较×高小较 方程 x3-β(α-β)x+αβ2=0 依今问正数,α=680,β=30,代入,求得x=120。 将如积同数式两端同除以高小较,并注意到勾股恒等式(4), 整理, 即 通弦×高和较=通和较×高弦 此式显然成立。且通和较,高和较及通弦已由α、β、x表出,只需将高弦表出。逆推即得。 (3)卷4第14题 通弦、边和求圆径。 记通弦=α,边和=β,半径=x,则 边小和=通弦+半径=α+x, 平勾=边小较=边小和-边和=α+x-β 合勾=平勾+半径=α+2x-β,平股=半径=x 合较和=合大和-合勾=边和-合勾=2β-α-2x,通和=通弦+径=α+2x 如积同数式 平勾×通和×合较和=2半径×边和×合勾 方程 4x3+4(2α-β)x2+(5α2+2β2-8αβ)x+α(α2+2β2-3αβ)=0 依今问正数,α=680,β=736,代入,求得x=120。 将如积同数式两端除以2边和,并注意到勾股恒等式(11), 整理, 即 半径×合勾=平勾×合股 亦即 平股×合勾=平勾×合股 此式显然成立。且平勾,合勾及平股已由α、β、x表出,只需将合股表出。逆推即得。 (4)卷4第17题 通弦、边和较求圆径。 记通弦=α,边和较=β,半径=x,则 通和较=大差较较=径=2x,大差勾=边和较=β 大差小较=大差较较-大差勾=2x-β,大差和较=大差勾-大差小较=2β-2x 通和和=2通弦+径=2α+2x 如积同数式 通和和×大差和较×大差小较=4半径2×边和较 方程 2x3+2(α-β)x2-β(3α-β)+αβ2=0 依今问正数,α=680,β=192,代入,求得x=120。 将如积同数式两端同除以大差小较,并注意到勾股恒等式(4), 整理, 即 通和和×大差和较=通和较×大差和和 此式显然成立。且通和较,大差和较及通和和已由α、β、x表出,只需将大差和和表出。逆推即得。 (5)卷4第19题 通弦、边勾求圆径。 记通弦=α,边勾=β,半径=x,则 平弦=边勾-半径=β-x,边弦=通弦-平弦=α-β+x 如积同数式 通弦×(平弦×边勾+半径×边弦)=平弦×通和×边弦 方程 2x3+4(α-β)x2+2(α2+β2-3αβ)x-αβ(α-2β)=0 依今问正数,α=680,β=256,代入,求得x=120。 将如积同数式两端同除以平弦,整理, 即 通和×边弦=通弦×边和 此式显然成立。且通弦,边弦及通和已由α、β、x表出,只需将边和表出。逆推即得。 (6)卷4第20题 通弦、边大和求圆径。 记通弦=α,边大和=β,半径=x,则 边小和=通弦+半径=α+x,边和和+边弦=边小和+边大和=α+x+β 如积同数式 [边大和×(通和和+通弦)]2=(边小和+边大和)2×边大和×通和和 方程 2x3+6αx2+(6α2+2β2-4αβ)x+α(2α2+2β2-5αβ)=0 依今问正数,α=680,β=1024,代入,求得x=120。 将如积同数式两端开平方,并注意到勾股恒等式(15), 边和和2=2边大和×边小和 整理, 即 边大和×(通和和+通弦)= (边和和+边弦)×通大和 此式显然成立。且(边和和+边弦),(通和和+通弦)及边大和已由α、β、x表出,只需将通大和表出。逆推即得。 由以上各题可知,如积同数式化简的结果是一个四项比例式。因而,建立方程的难点是确定式中的各项。据原文之“释曰”、“草曰”可以推测,比例四项的确定应由易至难分步进行。首先确定两相似勾股形对应的两项,其次确定第三项。由此可推知比例式。最后确定第四项。以第(1)题为例,据已知条件及所设未知元,先确定虚和和、通和和,次确定虚小较,得比例式,后确定通小较。整理即得如积同数式。已知2事求圆径,一题可有多种解法,而刘岳云则多题以一法求解。显然,其意在说明“比例之理、相等之数”的一般性。 《测圆海镜》讨论的问题是《九章算术》勾股容方与勾股容圆的推广。《九章算术》勾股章第14题、第15题分别由勾股形的2事求其内容方边、内容圆径。[18]《测圆海镜》圆城图式以半径为容方边使容方、容圆集中在一个图形之中,又将勾股形增加至16个。圆城图式与识别杂记的主要成果包括,勾股容圆概念的扩充、“九容”的确定、诸勾股形“五和五较”等量关系的表述、九容公式与圆径幂公式的建立。在此基础上,又运用天元术建立方程求解圆径。自《九章算术》上述两题的刘徽注文之后,容方与容圆问题的讨论极少。《测圆海镜》丰富了勾股算术的内容,为勾股测圆术的内容形成系统奠定了基础。 十三率勾股形的确定使勾股测圆术的内容形成系统,而以圆城图式添加过圆心且与通弦平行的线段为之关键。圆城图式的16形之中,删去重复者,共得11形。由识别杂记知,极形的13事之中,有11事与此11形的弦一一对应相等。而所载极和为“高弦平弦共”,极较为“明股内去叀勾”。极和、极较并无与之对应的勾股形的弦。又,11形之中,高形、平形与圆均未构成相容的位置关系。这两个问题不解决,十三率勾股形无从确定。在《测圆海镜》中,“弦上容圆”凡两见,即卷2第5题与卷11第6题。依题目数据推算,前题过圆心的弦与通弦不平行,后题平行。若将后题的弦画在圆城图式上,则高、平、合、断四形各得其位。由此,十三率勾股形容易确定。《测圆海镜》未能完成这一工作的原因,当与中国传统数学缺少明确的平行线概念有关。 勾股测圆术内容的系统化及其理论的概括与运用是晚清数学的一项重要工作。其中,刘岳云的工作可以简图表示如下: 从独立的70事中任取2事作为已知条件求解圆径,所取的2事或在或不在同一率勾股形中。当在同一率勾股形时,解此勾股形,再运用该率勾股形的圆径公式即可。当不在同一率勾股形时,若满足圆径幂公式的条件则开平方即可;若否,立天元建立圆径方程。故这一简图可以视为“比例之理、相等之数”的诠释,亦可说明勾股测圆术已臻完善。自容方、容圆以至于此,其间的轨迹大致如下: 容方、容圆——九容 ——十三容 ——比例、等数 ——圆径 考察晚清勾股测圆术的工作可见,当时的算家能够比较熟练地运用平行线、中垂线、汉译代数符号等西方数学知识。此为勾股测圆术得以发展与完善的重要原因。
4 十三率勾股形的等量关系补证


5 主要等量关系与勾股恒等式的变换


6 等量关系运用举例





7 十三率勾股形圆径诸公式补证








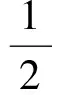
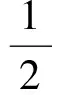


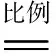
8 《测圆海镜通释》校改

9 “如积同数式”补证

高较较=高勾+高小较=x+β
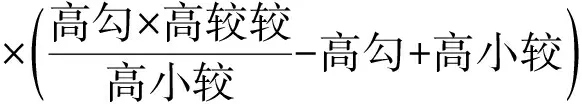




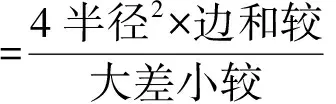
通和=通弦+径=α+2x,平股=半径=x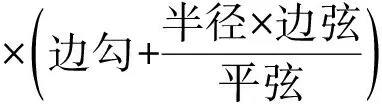
通和和=2通弦+径=2α+2x,通和和+通弦=3α+2x