弹性高超声速滑翔飞行器的状态/参数联合估计
陈尔康,荆武兴,高长生
哈尔滨工业大学 航天学院,哈尔滨 150001
高超声速滑翔飞行器一般指在大气层内以马赫数大于5的高速[1]作无动力滑翔的飞行器。为在大气层内高速飞行,高超声速滑翔飞行器一般采用细长体外形[2]并使用碳纤维等轻质复合材料,结构质量较小,因此弹性振动模态固有频率较低,弹性振动与刚体运动间存在不可忽略的耦合效应[3-4]。此外,在现代飞行器上广泛应用的高增益数字控制系统具有较大带宽,与高超声速滑翔飞行器的弹性振动模态固有频率接近,又会引起弹性振动和控制系统间相互耦合的气动伺服弹性问题[5]:导弹的结构弹性振动信号与刚体运动信号通过传感器送至控制系统,经处理后驱动舵面偏转,而舵面偏转所产生的力又会激励结构的弹性振动。文献[6]研究了弹性导弹的气动伺服弹性问题,发现弹性振动对惯导的测量信号有很大影响,惯导位置选取不当可能导致失稳。综上,在高超声速滑翔飞行器的总体设计和控制系统设计中必须考虑其结构弹性[7]。
但是传统的控制律都是基于刚体模型设计的。为抑制弹性振动模态对控制系统的不利影响,可在控制回路中加入陷波器,或通过反馈挠度等测量信号进行主动振动抑制控制[8]。这些方法都需要精确已知弹性振动的模态信息,但这些信息很难准确计算或直接测量。在过去的几十年中,自适应控制[9]等控制方法被用于弹性高超声速飞行器的控制器设计,有效提高了控制性能。这些方法将弹性模态作为扰动处理,虽然能够保证稳定性,但对控制性能有不利影响。因此,为实现对弹性高超声速飞行器的高精度控制,需要对弹性状态进行估计,并将其用于模型预测控制[10]、滑模控制[11]等先进控制方法。除状态以外,弹性振动模态的固有频率和振型等参数对飞行器的动态特性有很大影响,在状态估计、控制器设计和故障诊断等应用中十分重要。但这些参数很难在地面准确测得,且受飞行器状态和飞行环境影响而并非常值[12],因此对其进行实时估计同样是十分必要的。针对这一问题,文献[13-14]对参数进行估计,并将估计结果用于高超声速飞行器的自适应控制。但这类方法只对参数进行估计,无法实现状态和参数的联合估计。因此,开展对弹性高超声速滑翔飞行器状态/参数联合估计方法[15]的研究是十分必要的。
作为一种基于模型的递归滤波器,扩展卡尔曼滤波(Extended Kalman Filter,EKF)利用线性化技术对卡尔曼滤波进行扩展以用于非线性系统,现已广泛用于状态/参数估计、故障诊断和组合导航[16]等领域。但是EKF难以处理约束和参数不确定性,而这正是滚动时域估计(Moving Horizon Estimation,MHE)的优势。
MHE利用一段时间内的测量值,将估计问题转化为优化问题进行求解,因此能够处理带有约束的状态与参数联合估计问题,且具有更好的鲁棒性和估计精度[17-18]。MHE的优化目标函数由过程噪声、量测噪声和到达代价组成[19]。到达代价描述了历史数据对估计的影响,是保证MHE稳定性的关键[20]。传统的到达代价计算方法从概率和统计的角度出发,采用估计协方差矩阵计算到达代价[21],但这类方法并未充分利用滚动时域估计的结果,在非线性较强的情况下存在估计精度较差和结果发散的问题。
事实上,估计精度不仅与估计方法有关,还与传感器布置有关。对于高超声速飞行器常用的速率陀螺,其量测信号中同时包含刚体分量和弹性分量,可以在不增加额外传感器的情况下用来估计弹性状态和参数。但陀螺位置会影响量测信号中弹性分量的大小,进而影响系统可观性和估计精度[22]。因此还需要对速率陀螺的布置方案展开研究。
为了实现弹性高超声速滑翔飞行器的状态和参数联合估计,本文提出了一种传感器布置策略和一种利用正交三角(QR)分解更新到达代价的滚动时域估计算法(Moving Horizon Estimation with arrival cost updated by QR decomposition,MHE-QR)。通过对陀螺位置的优化提高了系统可观性,并在最优布置方案下利用MHE-QR算法对状态和参数进行联合估计。MHE-QR算法将到达代价的计算问题转化为最小二乘问题并利用QR分解进行求解,能够保证算法稳定性,有效提高了估计精度和计算速度。
1 弹性高超声速滑翔飞行器的数学模型
本文研究的弹性高超声速滑翔飞行器具有如图1所示的双锥体外形,其几何参数如表1所示。
由于高超声速滑翔飞行器结构弹性的主要来源是纵向弯曲,因此本文使用的纵向动力学模型为[5]
(1)
式中:m为飞行器质量;V为飞行器速度大小;θ为弹道倾角;L为升力;g为重力加速度;ϑ为俯仰角;q为俯仰角速度;M为俯仰力矩;I为转动惯量;α为迎角;ηi、ζi、ωi和Ni分别为第i阶弹性模态的广义坐标、阻尼比、固有频率和广义力。

图1 弹性高超声速滑翔飞行器几何外形Fig.1 Flexible hypersonic glide vehicle geometry

表1 几何参数Table 1 Geometry parameters
为估计飞行器状态、弹性模态固有频率和振型信息,弹性高速飞行器的传感器输出为4个速率陀螺的角速度信号qm,j[12]:
(2)
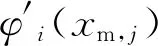

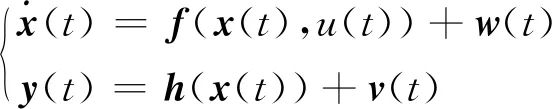
(3)
式中:w(t)为过程噪声;v(t)为量测噪声;函数f描述了系统动力学;函数h描述了系统输出。
由于MHE处理的是离散系统,因此利用多重打靶法将系统(3)离散:
(4)
2 传感器布置策略
传感器布置可视为一个优化问题,其中优化指标的选择较为关键。由陀螺的量测模型(2)可知,陀螺测得的角速度由刚体分量和弹性分量组成。当陀螺位于振型斜率为零处时,其测得的角速度中不含弹性分量,这对弹性状态和参数的估计是非常不利的。较好的传感器布置方案应使得测量信号中包含较多的弹性分量以减小估计误差。因此应选择能够反映系统可观测度的优化指标。传统的可观性判据只能判断状态是否可观,不适合作为优化指标。在这方面,Popov-Belevitch-Hautus(PBH)判据的改进形式能够反映系统可观测度,可选为性能指标[22-23]。该性能指标由PBH判据导出,PBH判据的具体内容如下所述。
考虑式(5)所示的系统:
(5)
若对于Ae的每一个特征值λi,式(6)均成立,则该系统是可观的。
rank(PBH(λi,Ae,Ce))=n
(6)
式中:n为Ae的维数,PBH(λi,Ae,Ce)为式(7)所示的PBH矩阵:
(7)
式中:In为n维单位矩阵。
PBH矩阵的每个条件数能够描述其对应模态的可观测度。每个条件数越大,其对应的模态就越接近不可观[21]。因此,优化指标J选为所有PBH矩阵条件数中的最大值,即
J=max(cond(PBH(λi,Ae,Ce)))i=1,2,…,n
(8)
式中:Ae和Ce可由式(1)~式(3)经线性化得到。
在仅考虑一阶弹性振动模态的情况下,传感器位置与性能指标间的关系如图2所示。当陀螺位于飞行器中部时,性能指标最大,可观测度最差。此时陀螺测量信号中几乎不含弹性分量,对状态/参数的估计非常不利。而布置在飞行器头部或尾部时,陀螺测量信号中弹性分量较大,对状态/参数估计较为有利。因此上述优化指标的选择是合理的。
在考虑三阶弹性模态的情况下,单传感器位置与性能指标间的关系如图3所示。受二阶和三阶弹性模态的影响,一些位置的可观测度变差,传感器位置与性能指标间的关系变的复杂。
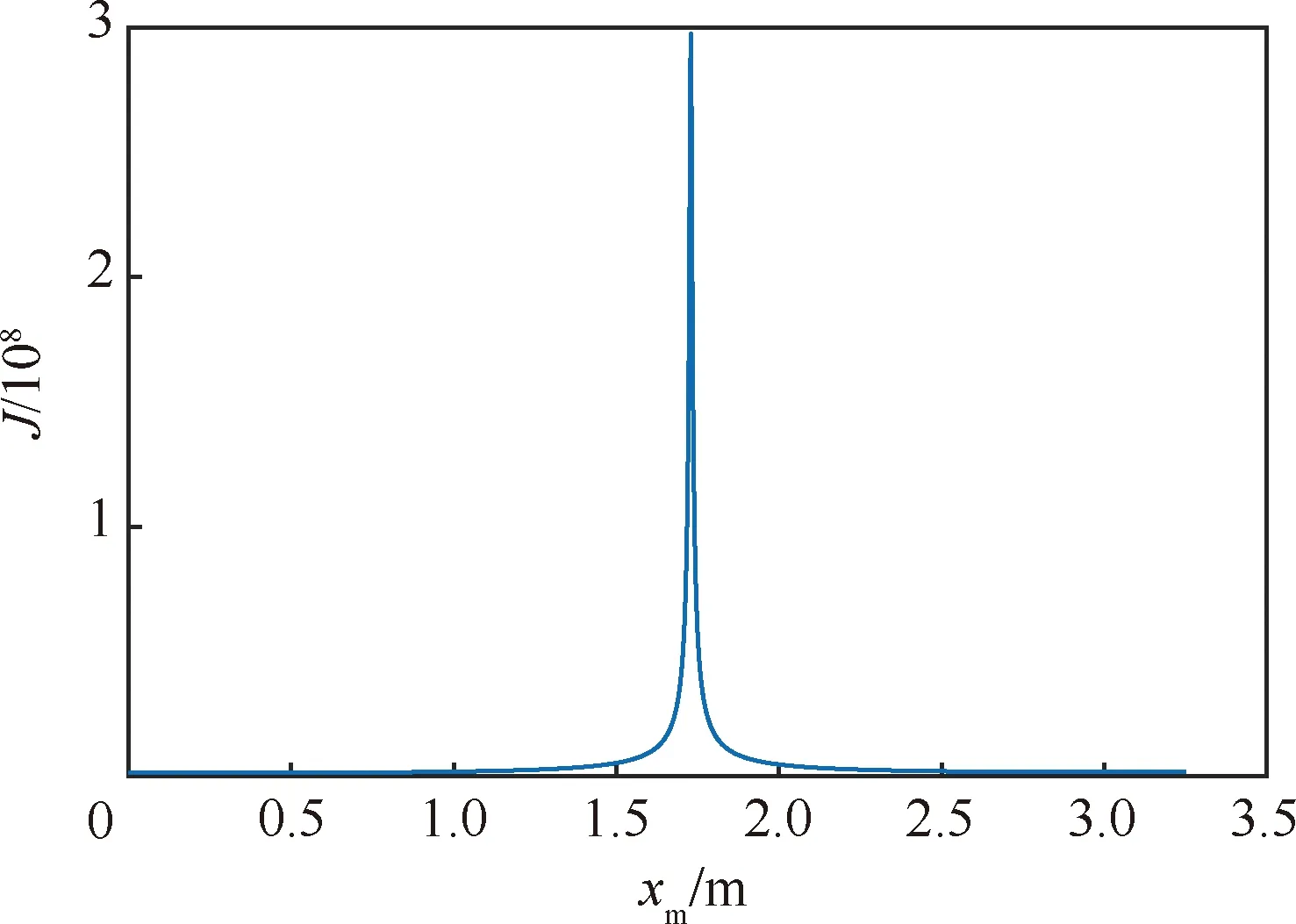
图2 单传感器位置与性能指标间的关系(一阶)Fig.2 Relationship between single sensor position and performance index (one order)

图3 单传感器位置与性能指标间的关系(三阶)Fig.3 Relationship between single sensor position and performance index(three orders)
因此,多传感器的布置方案需要通过优化确定。最终,多传感器布置问题被转化为如下优化问题:
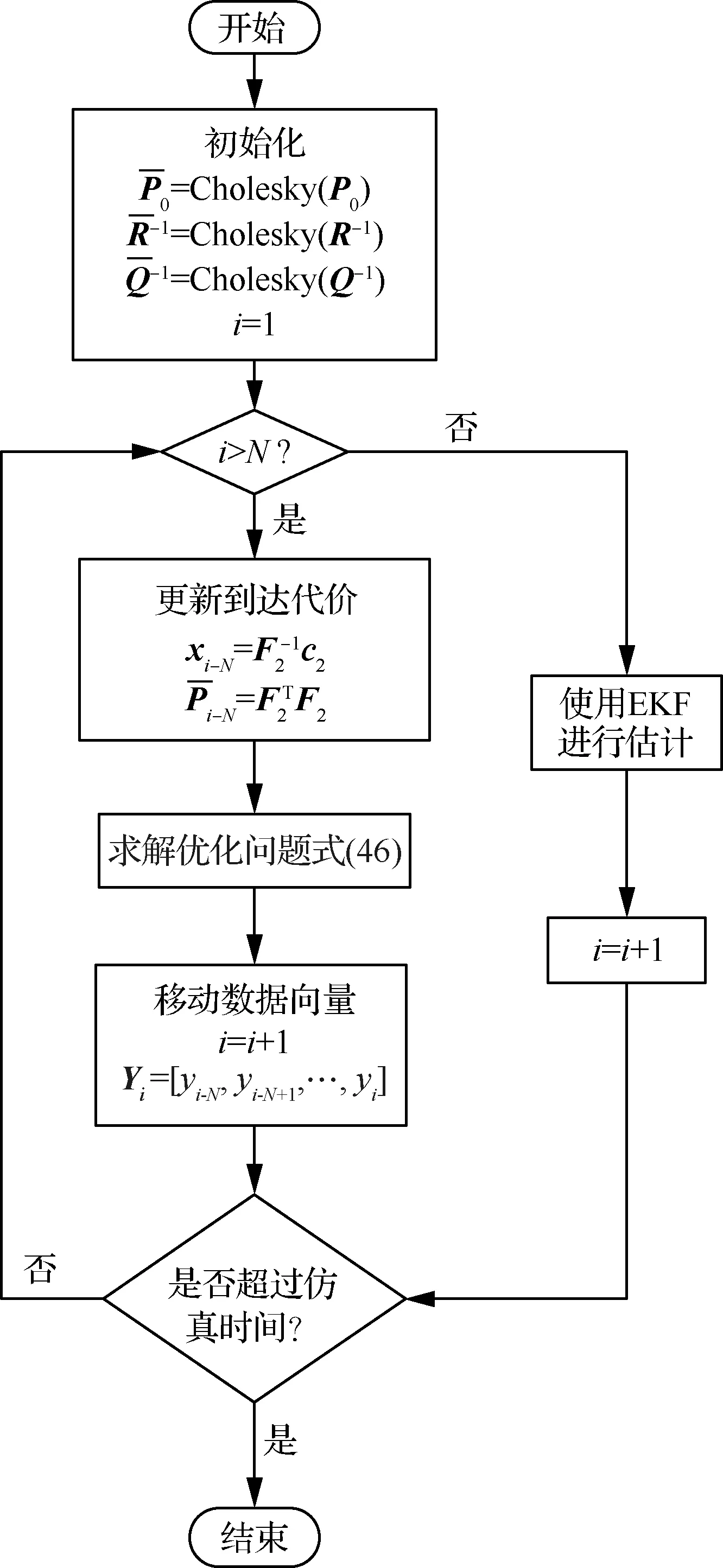
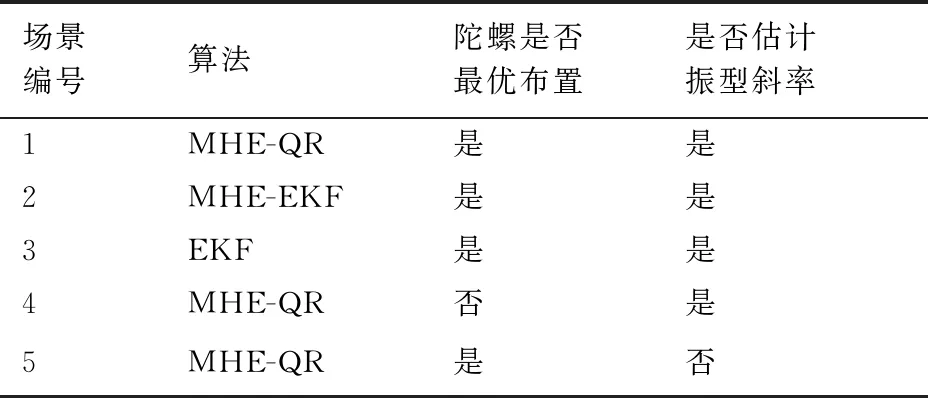
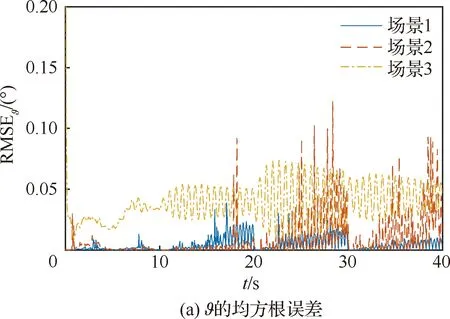
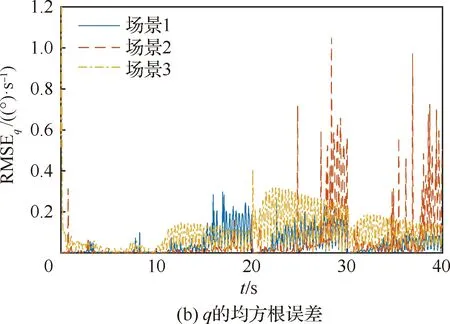
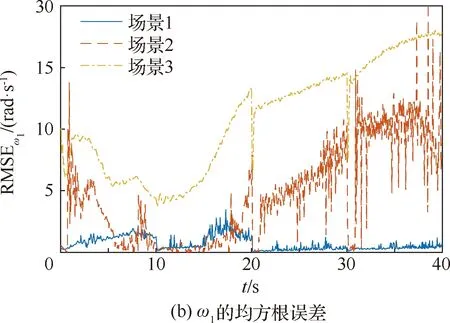
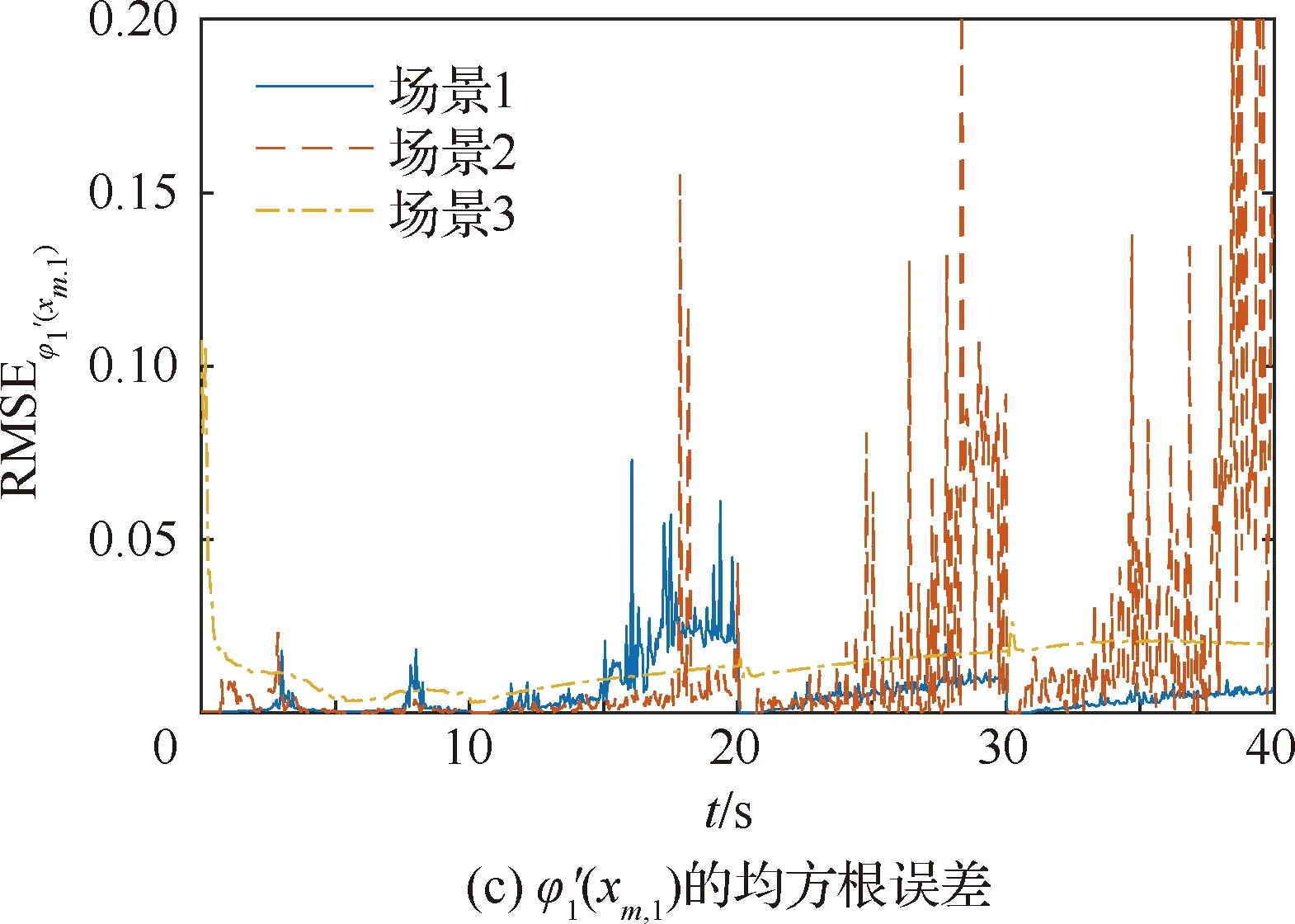
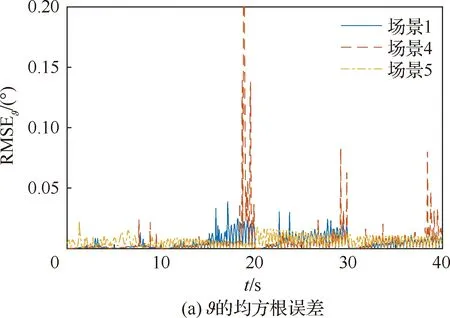
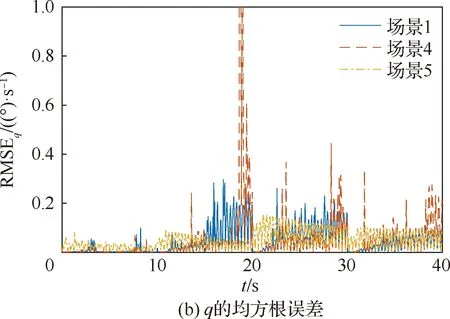
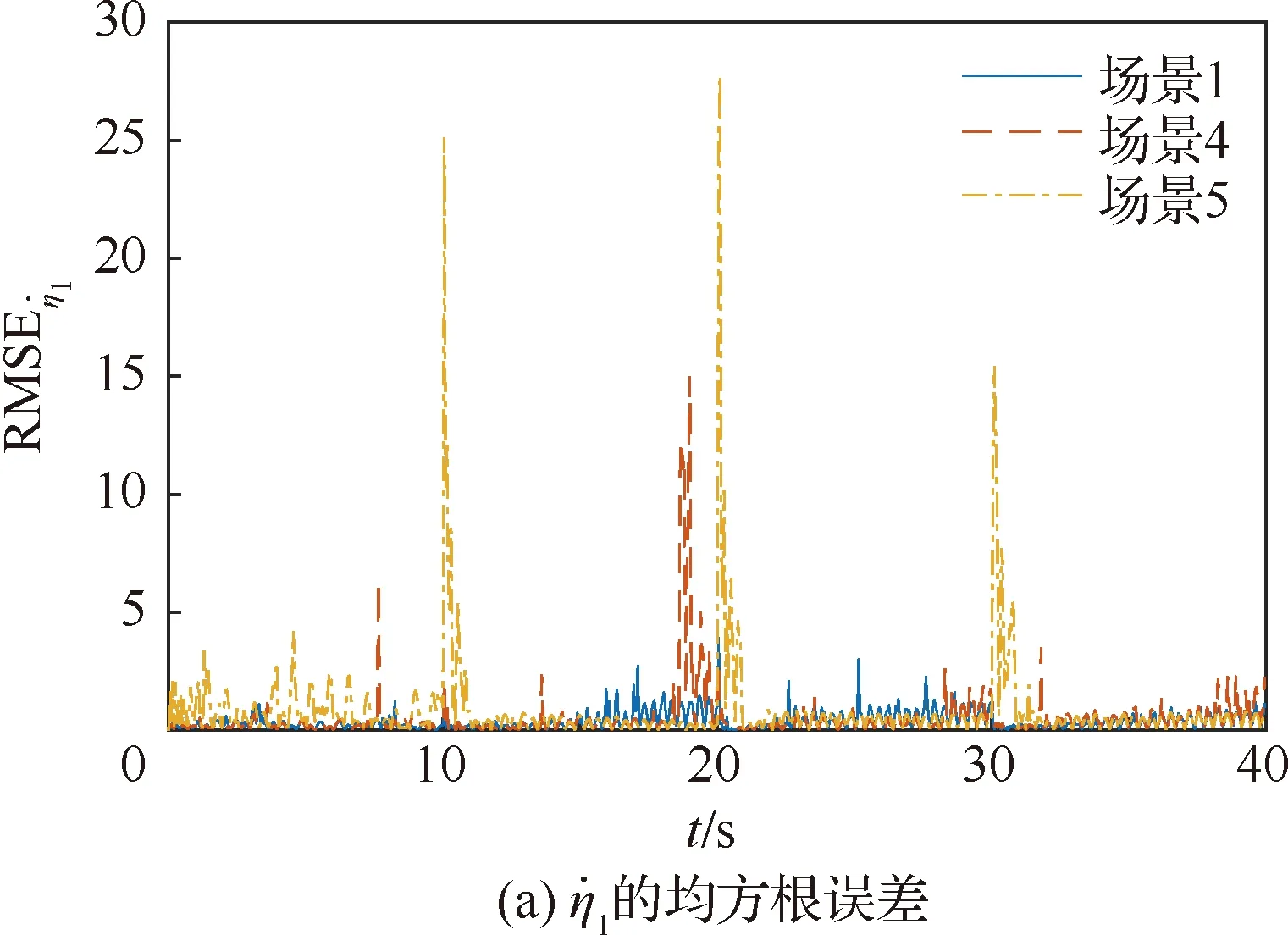
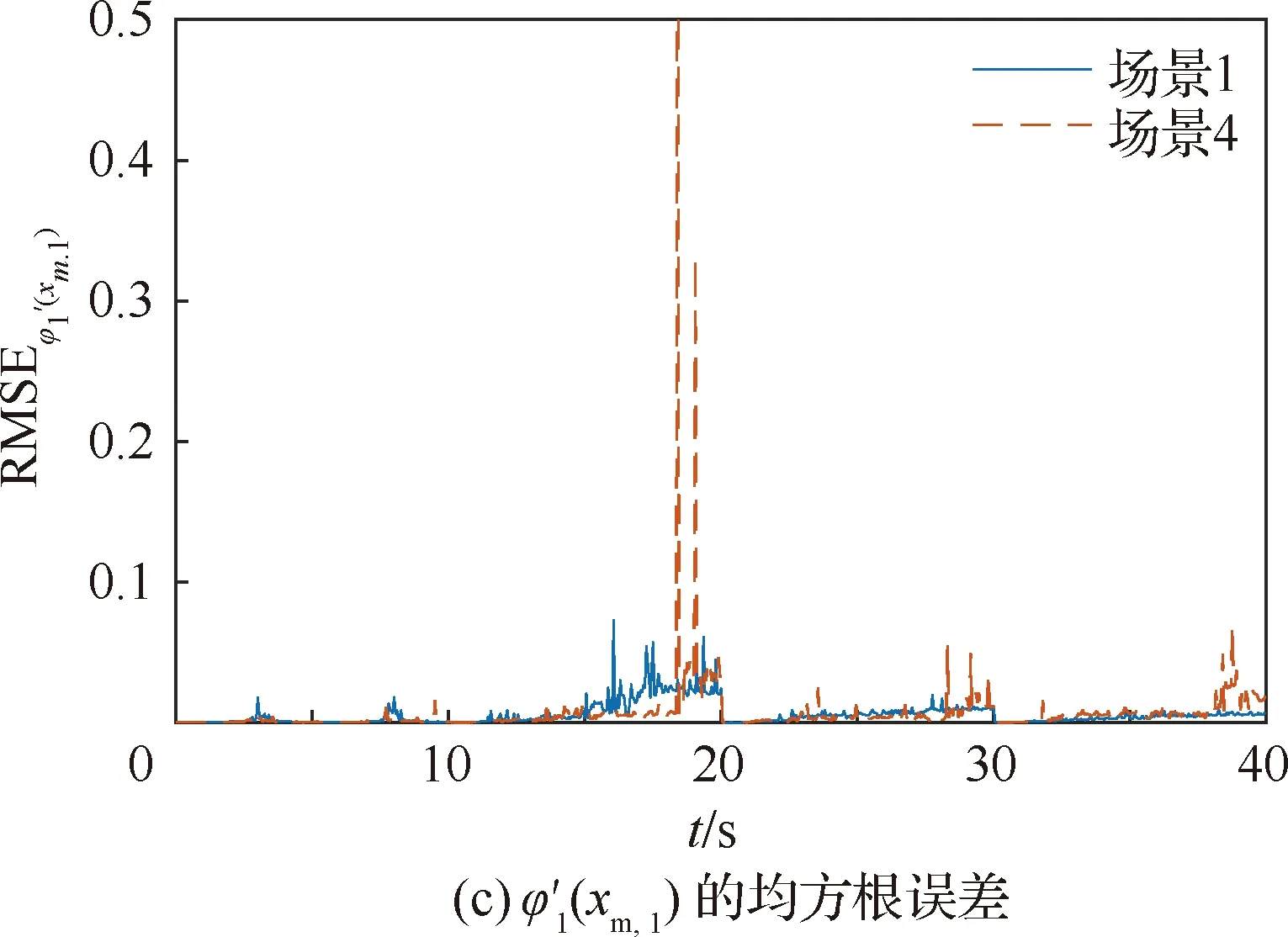
s.t.xmin xm,i+1-xm,i>lmin (9) 式中:xmin和xmax分别为陀螺到飞行器头部的最小和最大距离;lmin为相邻两个陀螺间的最小距离。本文中xmin、xmax和lmin的取值如表2所示。 利用序列二次规划算法求解优化问题(9)即可得到最优传感器布置方案,如表3所示。 表2 传感器布置参数Table 2 Sensor placement parameters 表3 传感器布置方案Table 3 Sensor placement scheme 在本文中,为表示方便,采用如下记法: (10) (11) 式中:a为m维向量;W为m×m维矩阵。 记滚动窗口长度为N。MHE利用当前时刻之前N个时间点的数据,将状态/参数估计问题转化为优化问题: (12) s.t. (13) 式中:wk为过程噪声;Q为过程噪声协方差矩阵,vk为量测噪声;R为量测噪声协方差矩阵。ΘT-N(xT-N)为到达代价,到达代价概括了滚动窗口之前的数据,对MHE的性能和稳定性有很大的影响。 根据MHE问题的定义和前向动态规划原理,到达代价的定义为[20]: (14) s.t. xk+1=F(xk,uk)+wkk=0,1,…,T-N-1 (15) 由式(14)和式(15)可知,到达代价的计算较为复杂,对于约束非线性系统更是无法得到解析表达式[20]。因此一般采用二次函数估算到达代价,即 (16) PT-N=Q+GPT-N-1GT- GPT-N-1C(R+CPT-N-1CT)CPT-N-1GT (17) (18) 在本文中,利用式(17)更新到达代价的MHE算法称为利用EKF更新到达代价的滚动时域估计方法(Moving Horizon Estimation with arrival cost updated by EKF,MHE-EKF)。MHE-EKF算法未能充分利用MHE的估计结果,难以进一步提高MHE的估计精度和计算速度。对此,本文在确定性框架下给出一种利用QR分解更新到达代价的算法。 由式(14)可知,T+1时刻的到达代价为 (19) 根据前向动态规划原理和式(14),式(19)可改写为 (20) s.t. (21) 利用近似到达代价代替到达代价,将式(16)代入式(19)可得 (22) 为表示方便,对权重矩阵作Cholesky分解可得 (23) (24) (25) 式中: (26) 将式(25)代入式(24)可得 (27) 至此,到达代价的更新问题被转化为如下最小二乘问题: (28) 式中: (29) 为保证数值稳定性和提高计算速度,使用QR分解求解这一最小二乘问题。对A作QR分解可得 (30) 式中:E为正交矩阵;F1和F2为上三角矩阵。设 (31) 由式(29)~式(31)可得 (32) 显然可得此最小二乘问题的解为 (33) 将式(33)代入式(28)可得 (34) 由式(34)可得到达代价更新的递推方程为 (35) 基于QR分解的到达代价更新算法根据上一时刻MHE的估计结果计算到达代价,且能够保证数值稳定性,能够提高MHE的估计精度和计算速度。此外,该到达代价更新算法还具有如下性质。 (36) (37) 注2该到达代价更新算法给出的到达代价是有界的,说明历史数据对估计结果的影响是有限度的,不会无限增大。即对于任意向量v,有 (38) 式中:λmax为矩阵Q-1最大的特征值。 由式(29)可得 (39) 由式(30)可得 (40) 比较式(39)和式(40)等号右侧矩阵第2行第2列元素可得 (41) 由式(35)和式(41)可知,对于任意向量v,有 (42) 注3该到达代价更新算法能够保证MHE的稳定性。 根据式(20),该到达代价算法具有如下性质: (43) 反复应用式(43)可得 (44) 式(44)表明该达到代价更新算法满足文献[20] 中的条件C2: (45) 因此根据文献[20]中的命题3.4,该到达代价算法能够保证MHE的稳定性。 在3.2节提出的到达代价更新算法的基础上,利用序列二次规划算法求解式(46)所示的优化问题即可实现对状态和参数的估计,形成MHE-QR算法。 (46) s.t. (47) MHE算法的流程如图4所示。 图4 滚动时域估计算法流程图Fig.4 Flow chart of MHE 在仿真中,窗口长度设为N=15,采样周期为Δt=0.05 s,量测噪声方差矩阵为R=diag(2.5×10-5,2.5×10-5,2.5×10-5,2.5×10-5),系统噪声方差矩阵为Q=diag(1×10-6,1× 10-2,1×10-6,2.5×10-3)。对一阶弹性模态固有频率和振型斜率加入了正弦扰动信号。为了验证不同输入下算法的性能,系统输入信号如图5 所示。 为验证传感器布置策略,并分析MHE-QR、MHE-EKF和EKF 3种算法的性能,分别在表4所示的仿真场景下进行仿真。 在相同条件下分别使用MHE-QR(场景1)、MHE-EKF(场景2)和EKF(场景3)3种算法进行蒙特卡罗仿真,均方根误差(Root Mean Square Error,RMSE)如图6和图7所示。 图5 输入信号Fig.5 Input signal 表4 仿真场景Table 4 Simulation cases 图6 不同算法下ϑ、q和η1的均方根误差Fig.6 RMSE of ϑ、qandη1 with different algorithms 图7 不同算法下和的均方根误差 different algorithms 同样使用MHE-QR算法,分别在传感器最优布置(场景1)、传感器非最优布置(场景4)和不估计振型斜率(场景5)的情况下进行蒙特卡罗仿真,均方根误差如图8和图9所示。 由图8和图9可知,由于传感器并非最优布置,场景4的RMSE存在较多的突然增大的情况,估计误差大于采用最优传感器最优布置的场景1。而在15~20 s的时间段内,由于系统状态已经收敛至稳态值,虽然场景1的均方根误差大于场景4和场景5,但场景4和场景5均存在均方根误差突然增大的情况,这对实际应用非常不利。因此,仿真结果表明传感器非最优布置对估计精度有不利影响。此外,受不对振型斜率进行估计的影响,场景5中弹性状态和弹性模态固有频率的RMSE均显著大于场景1和场景4,说明振型斜率的偏差对估计结果影响较大。因此,传感器布置策略和包含振型斜率的状态/参数联合估计能够有效提高估计精度。 图8 不同传感器布置下ϑ、q和η1的均方根误差Fig.8 RMSE of ϑ、q and η1 with different sensor placements 图9 不同传感器布置下的均方根误差Fig.9 RMSE of with different sensor placements 对于估计算法的实际应用,计算耗时是非常重要的。表5给出了不同场景下的计算耗时,仿真在Windows 10系统(CPU为i5-7400,主频为3.00 GHz)中MATLAB R2017a环境下完成。其中EKF(场景3)的耗时明显短于其他算法,而MHE-QR(场景1、4、5)的平均耗时短于MHE-EKF。虽然同样使用MHE-QR算法,但传感器非最优布置的场景4的最大耗时是所有场景中最大的,说明传感器最优布置能够缩短计算耗时。由于估计状态数量最小,场景5的平均耗时和最大耗时都是使用MHE-QR算法的所有场景中最小的,但其估计精度较差,难以实际应用。而场景1则在估计精度和计算耗时之间做到了较好的平衡。得益于传感器最优布置和基于QR分解的到达代价更新策略,场景1的估计精度是最高的,但其平均耗时和最大耗时都仅长于使用EKF的场景2和不估计振型斜率的场景5,且其最大耗时并未超出采样周期,表明其具备实时应用潜力。因此,本文提出的传感器布置策略和到达代价更新策略不仅能够提高估计精度,也能够提高计算速度。 表5 计算耗时Table 5 CPU time consumption 1)为提高弹性高超声速滑翔飞行器的状态/参数估计精度,本文提出了一种传感器布置优化方法。该优化方法选择PBH矩阵条件数的最大值为优化指标。仿真结果表明,传感器布置优化方法能够有效提高状态/参数的估计精度。 2)针对弹性高超声速滑翔飞行器的状态/参数联合估计问题,本文提出一种新型的滚动时域估计算法——MHE-QR算法。该算法将到达代价的估计问题转化为最小二乘问题,并给出一种新型的利用QR分解更新到达代价的算法。MHE-QR算法限制了到达代价过度增长,能够保证滚动时域估计算法的稳定性。仿真结果表明,MHE-QR算法的估计精度高于EKF和MHE-EKF算法。此外,MHE-QR的计算耗时小于采样周期,具备实时应用的潜力。 后续需要研究滚动时域估计算法的数值求解方法,以进一步提高计算速度,满足实时应用的要求。

3 滚动时域估计
3.1 问题描述
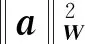
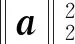
3.2 到达代价更新算法

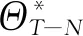

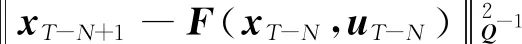

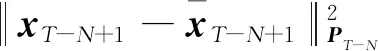
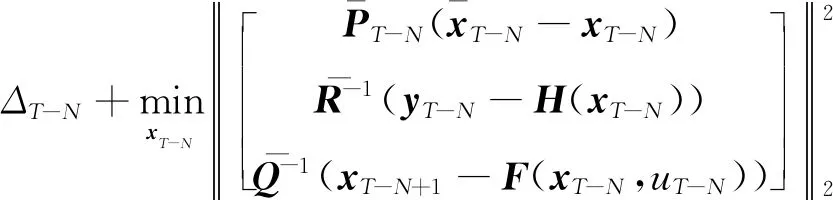
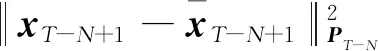
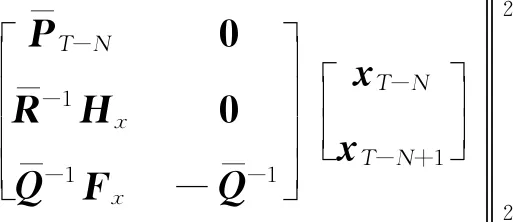

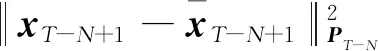
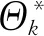
3.3 MHE的数值解法
4 仿真分析







5 结 论

