非圆形截面直梁的自由振动

高珊珊 黄欣 郝颖

摘 要：本文以空间曲梁理论为基础，推导出具有非圆形横截面的直梁的运动微分方程，对其自由振动特性进行研究。方程中不仅考虑了转动惯量、轴向变形和横向剪切变形的效应，而且考虑了与扭转有关的翘曲变形对梁固有频率的影响。结果表明：在考虑了翘曲效应后，用本文方法得到的解和有限元结果吻合得很好，翘曲变形对梁的第5—8阶固有频率有较大影响。

关键词：非圆形截面;广义翘曲坐标;固有频率

中图分类号：O326;TU323 文献标识码：A 文章编号：1003-5168（2019）28-0110-02

Free Vibration Analysis of Straight Beam with Non-circular Cross Section

GAO Shanshan HUANG Xin HAO Ying

（School of Civil Engineering and Communication， North China University of Water Resources and Electric Power，Zhengzhou Henan 450045）

Abstract： Based on the spatial curved beam theory， the differential equations of motion for straight beam with non-circular cross section were derived， and its free vibration characteristics were studied. In the formulations， the warping effect upon natural frequencies was studied in addition to considering the rotary inertia， the shear and axial deformation effects. The numerical result shows that the results available in the literature are consistent with the finite element results by considering the warping effect， which has a great influence on the 5th-8th order natural frequencies of the beam.

Keywords： non-circular cross section;generalized warping coordinate;natural frequency

梁是大型空间结构的重要组成构件之一。在实际工程中，梁不可避免地会受到动荷载的作用，其在动荷载作用下振动时的受力情况和表现与静荷载作用时有很大差别，是设计中必须要考虑的问题。

但目前，已有研究大多考虑了转动惯量、轴向和横向剪切变形中的一种或几种[1-3]，很少见到在梁的运动微分方程中计及横截面翘曲变形的影响。本文推导出一组描述梁自由振动的方程，其由14个微分方程相互耦合而成，且加入了广义翘曲坐标和广义翘曲力矩两个自由度后，方程呈现出很强的刚性，求解较为困难。本文采用改进的Riccati传递矩阵法来求解上述运动微分方程。结果表明：直梁横截面的翘曲变形，对前4阶频率影响较小，但对第5—8阶频率有较大影响，是动力学分析中应该考虑的因素。

1 几何关系和基本假设

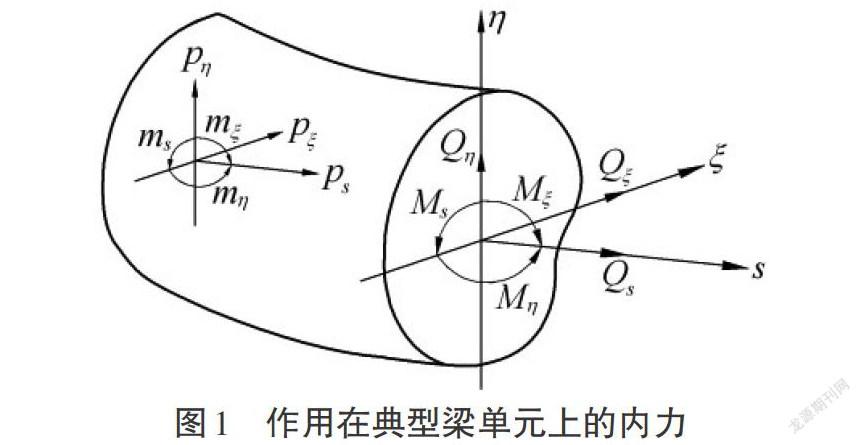
取[ξ， η]轴为过梁横截面的形心[ξ， η]的主轴，[s]为沿梁的轴线方向的弧坐标，如图1所示。其中[Qs]是轴向力;[Qξ]和[Qη]是剪力;[Ms]是扭矩;[Mξ]和[Mη]是弯矩;[us（s，t），][uξ（s，t）]和[uη（s，t）]分别是位移矢量在[s]、[iξ]和[iη]方向的三个移动分量;[φs（s，t）]、[φξ（s，t）]和[φη（s，t）]分别是转角矢量在[s]、[iξ]和[iη]方向的三个转动分量;[φ（ξ，η）]是圣维南扭转翘曲函数;[α（s，t）]则是广义翘曲坐标。

研究的基本假设为梁横截面在自身所在的平面内是无限刚性即是不变形的，但在平面外会发生翘曲。

2 运动微分方程

假设梁的变形是由伸长、弯曲和扭转共同引起的，则位移场可以表示为：

[u（s，ξ，η，t）=W（s，ξ，η，t）t+U（s，ξ，η，t）iξ+V（s，ξ，η，t）iη]（1）

在動载荷作用下，[u=u（s，ξ，η，t）]既是坐标[ξ， ][η， ][s]的函数，也是时间[t]的函数。式中，[U]、[W]和[V]的计算公式为：

[U（s，ξ，η，t）=uξ（s，t）-ηφs（s，t），V（s，ξ，η，t）=uη（s，t）+ξφs（s，t）W（s，ξ，η，t）=us（s，t）+ηφξ（s，t）-ξφη（s，t）+α（s，t）φ（ξ，η）]（2）

假设[eξξ=eηη=eξη=0]，则横截面上的应变[ess]、[esξ]和[esη]的分布规律为：

[ess=εs+ηωξ-ξωη+φα′+ks∂φ∂ξη-∂φ∂ηξα2esξ=Gξεξ-φη-ηωs+∂φ∂ξ+kηφα2esη=Gηεη+φξ+ξωs+∂φ∂η+kξφα]（3）

其中

[εs=u′s-kηuξ+kξuη εξ=u′ξ-ksuη+kηusεη=u′η-kξus+ksuξωs=φ′s-kηφξ+kξφηωξ=φ′ξ-ksφη+kηφsωη=φ′η-kξφs+ksφξ]                       （4）

引入应力合力和合力矩为：

[Qs=σsdξdηQξ=τsξdξdηQη=τsηdξdηMs=τsηξ-τsξηdξdηMξ=σsηdξdηMη=-σsξdξdη]                   （5）

[u's=-1EA0Qsu'ξ=φη+1A0GGξQξu'η=-φξ+1A0GGηQηφ's=D5-D4Iηη+Iξξα+1G（Iηη+Iξξ）Msφ'ξ=1IξξMξφ'η=1IηηMηα'=1D8TQ's=-ρA0ω2usQ'ξ=-ρA0ω2uξQ'η=-ρA0ω2uηM'ξ=-ρIξξω2φξ+QηM'η=-ρIηηω2φη-QξT'=-G（D5+D4）ws+Gα（D9+D10）]                  （6）

把（3）式代入本构方程[σs=Eess， τsξ=2Gesξ， τsη=2Gesη]中，然后把所得结果再代入（5）式，即可得到用广义应变和广义翘曲坐标表示的等效本构方程。假设梁作频率为[ω]的简谐运动[5]，则可以得到如式（6）所示的一组运动微分方程。

本文采用改进的Riccati传递矩阵法[6]来求解弹簧的运动微分方程。

3 数值算例

矩形截面铝质两端固支的直梁，[ρ=2 700kg/m3，][μ=0.33，][E=71.7GPa]，截面的边长为[2a]和[2b]，梁的长度为[l]，扭转翘曲函数为：

[φξ，η=ξ×η-32a2π3n=0∞（-1）nsinh（2n+1）πη2a（2n+1）3cosh（2n+1）πb2asin（2n+1）πξ2a]   （8）

令[2a=0.1m， 2b=0.08m， l=1m]，在ANSYS中將上述梁划分为600个SOLID185单元。为了与有限元结果进行比较，采用本文方程计算该梁前8阶的固有频率（见表1）。

由表1可知，在考虑了翘曲效应后，用本文方法得到的解和有限元结果吻合得较好。翘曲变形对矩形截面梁的第5—8阶固有频率具有较大影响。

参考文献：

[1]夏呈.修正铁摩辛柯梁受迫振动响应分析及其应用[D].南京：东南大学，2017.

[2]李俊，金咸定.Timoshenko薄壁湾弯扭耦合振动的动态传递矩阵法[J].振动与击，2001（4）：57-59.

[3]李静斌，陈淮，葛素娟.考虑剪切变形及转动惯量的H型钢梁自由振动[J].铁道科学与工程报，2012（2）：29-33.

[4]虞爱民，郝颖，杨荣强.自然弯扭梁动力分析的精细积分法[J].同济大学学报（自然科学版），2009（10）：1323-1327.

[5]郝颖，虞爱民.考虑翘曲效应的圆柱螺旋弹簧的振动分析[J].力学学报，2011（3）：561-569.

[6]刘保国.一维不定参数结构系统的摄动Riccati传递矩阵方法及其应用[D].重庆：重庆大学，2002.