一堂“意外”的数学课
张雄波

由于数学课的开放性很强,我们的学生又是一群活泼可爱的少年,因此数学教学过程中也充满了太多的不确定因素。我们在备课中的一些预设,并非会按照我们设想的那样去完成。作为教师的我们在课堂上充满了太多的挑战。这需要教师有一双慧眼,能捕捉到课堂中有价值的信息,并将这种信息合理的,有效的利用,让课堂中的意外变成教学中的精彩。
八年级数学12.2.1作轴对称图形的最后一个内容是“探究”问题,我在课堂上经历了一系列意外,促成了良好的教学效果,自己对探究课的意义及组织有了更深的认识,现把课堂教学过程实录如下。
课本第42面给出了探究内容:
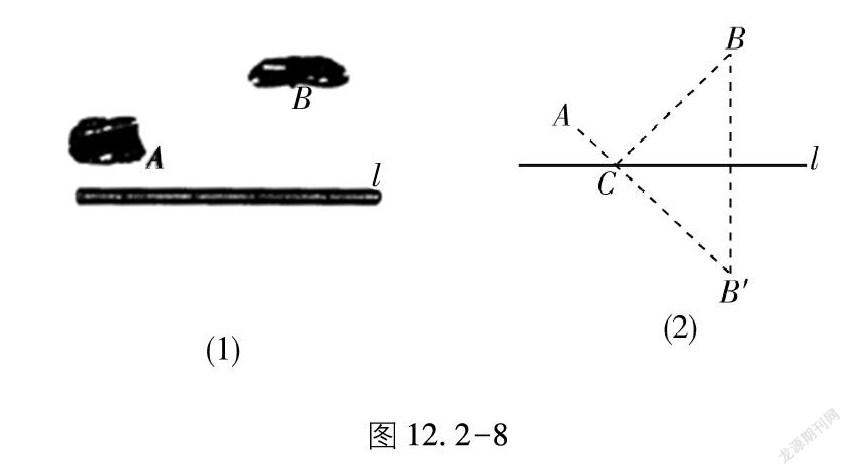
如图12.2-8(1),要在燃气管道l上修建一个泵站,分别向A,B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个 试一试,能发现什么规律?
我们可以把管道l近似地看成一条直线,A,B两镇近似地看成两个 (图12.2-8(2)),问题就是要在l上找一 C,使AC与CB的和最小.设B′是 B关于直线l的对称 ,本题就是要使AC与CB′的和最小.在连接AB′的所有线中,线段AB′最短.因此,线段AB′与直线l的交 C的位置即为所求.
为了证明 C的位置即为所求,我们不妨在直线l上任取一 C′(不与C重合),连接AC′,BC′,B′C′.
因为直线l是 B,B′的对称轴, C,C′在l上,所以CB=CB′,C′B=C′B′,
所以AC+CB=AC+CB′=AB′.
在△AC′B′中,
由三边关系可得AB′<AC′+C′B′,
所以AC+CB<AC′+C′B,
即AC+CB最小.
同年级其他班的数学老师教过该节内容,感觉学生似懂非懂。我担心教学效果差,就向学生强调预习好该节内容。课堂开始,我问:“多少人看懂了?”(没有一个人举手应答),气氛的沉闷让我意外。就算我讲下去,学生也只是被动接受。
我说:“现在同学们在直线l上找个 试下,只要能说出画法和自认为满足要求的理由,不要太在乎对错,更不必受课本解法的影响。”学生行动了,我看到学生甲找了一个 ,就要他发言,甲说:“先连接AB,再作线段AB的垂直平分线交l于 C,在 C处修泵站,理由是垂直平分线的性质:垂直平分线上的 到线段的两个端 的距离相等。”我一愣,这与问题要求毫不相关,正准备否定,却听到有学生发出轻声同感“我也是这样做。”这样一个错误的答案也有部分人响应,再次让我意外。我改变主意(甲正用期盼的眼神望着我),说:“甲勇于探索,找到了一个 ,大家要向他学习,并且他把刚学过的垂直平分线的性质用上了,得CA=CB,是否符合问题的要求,暂时不讨论,想问的是,还有谁像甲一样探索找到了别的 ?”
受甲的鼓舞,乙主动举手答:“过 A作l的垂线段,垂足为 C,在 C处修泵站,理由是垂线段最短。”我有些高兴,因为他的问答与问题的要求近了 ,正要评价(丙急忙举手,有观 迫切表达),我稍迟疑,还是让丙先说。“过 B作l的垂线段,垂足为 C,在C处修泵站,理由是垂线段最短,我用的道理和乙虽然一样,但我的做法照顾了B镇的人,毕竟他们离管道l远些,所以我认为自己的作法更好。”丙的话音刚落,班上马上出现了两派,和乙关系好的学生力挺乙的观 ,丙也有不少拥护者,一时争论难下,又有学生开始调和:“两个人的都对。”大家望着我,等我来评判。我说:“大家量一下两种情况下的CA+CB。”学生在书上画图,很快测量出乙的CA+CB=0.6+2.6=3.2 cm,丙的CA+CB=2.2+1.5=3.7 cm(丙的拥护者很失落,但仍有不服气的神色),丙站起说:“我和乙用的同样的道理,如果说我的错,那么他的也不一定对。”新的一轮争论又开始……,又有学生调和:“就在乙和丙找的两个垂足之间再找,可能是两个垂足的中 吧!”甲也说:“我的作法中,C 也在乙和丙的两个垂足之间,乙和丙不一定对,那么我的有可能对。”没有统一的观 ,教室里学生自发的争论,各抒己见,久违的活跃气氛让我意外。(我既欣喜,又焦急,看表已过了近17分钟,仍没进入正确的做法和分析,真不知今天的教学任务能不能完成)
不能破坏学生好不容易形成的积极性,我开始引导说:“大家认真思考了,也都有一定的道理,但因为有片面之处难以说服他人,请同学们按我的提示分步进行分析。”教室变得十分安静,我说:“首先,泵站C的地 有人认为是乙、丙所说的垂足,也有人认为在这两个垂足之间,都自觉地把C当成了一个动 来研究,请问动 C还会在其他位置吗?再研究一下。”很快乙举手答:“如果在我所说的垂足的左边,CA与CB都会变大,不可能。”丙也举手答:“如果在我所说的垂足的右边,CA与CB也都变大,不可能。”我继续引导:“看来泵站C只能在乙、丙所说的垂足上或两个垂足之间了,但同学们刚才的讨论始终没有一致结论,是否应该把CA,CB中的一条线段换下位置,再求和的最小值?”(学生若有所思,3分钟后有学生陆续举手)在我示意下,丁回答:“我发现课本上把CB换成CB′了。”我问:“B′是怎么作的?CB=CB′吗?AC+CB′在什么情况下最小?”丁说:“B关于直线l的对称 是B′。因为对称的线段相等,所以CB=CB′。A,C,B′共线时,AC+CB′最小,理由是两 之间线段最短。”(我在与丁的一问一答中,观察到许多学生紧皱的眉头舒展开,露出会意的笑容)我问:“听懂了丁的分析的同学请举手。”全班学生都自信地举起手。这又一次让我意外,难道学生突然变聪明了,可能是他们今天积极思考、听讲认真、学得主动的缘故吧!(我看了下时间,刚过了30分钟,估计今天的教学任务可完成)
接着,我训练学生写出规范的做法,严谨的说明过程。接近尾声,戊举手提问:“您作的是 B关于直线l的对称 B′,再连接AB′交l于 C,在 C处修泵站;我认为也可以作 A关于直线l的对称 A′,再连接A′B交l于 C,在 C处修泵站。那有两个 C怎么办呢?”学生们没想到戊提出个新的答案,又开始议论起来,也有人动笔画图。在集体研究中大家发现两个修泵站的 在作出的图中竟是重合的。至此问题圆满解决(距离下课还有5分钟,我布置了相关练习题,学生们跃跃欲试,后来从作业的批改来看,完成的情况良好)。
一直以来,我自以为对数学问题的理解和分析都很透彻,教学中尽显自己的主导作用,但效果平平。这堂探究课对学生放手,产生了意外的效果。在本节课初,我检查预习情况时气氛的沉闷,甲的错误答问让我意外,但这是班级的现状,不能回避。我没有选择自己主讲,也没有选择批评学生。接着乙和丙大胆地探究,以及围绕着两个人的结论展开的一轮又一轮的讨论使学习气氛异常活跃,让我意外,这是我的宽容、鼓励激发了学生潜在的积极性和智慧,出现百家争鸣的局面。最后,学生的探究活动在老师的引导下达到新的高度,丁给出精彩的回答,戊提出有价值的疑惑,学生接受知识的能力如此之高,又一次让我意外,这只说明在探究活动中学生一旦真正参与,成为学习的主人,全身心投入,学习就会成为乐趣,既轻松又高效。
探究性教学成为时代宠儿,源于它符合新的教育理念,信任学生的学习能力,营造宽松且不乏竞争性的课堂氛围,师生积极互动,共同发展,让学生在探索、讨论、实践、质疑中学习。探究性教学不但让学生获得知识,更让学生获得学习的能力。我的一堂课意外的良好效果正是一个有力的证据。
葉澜教授说过:课堂应是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的图景,而不是一切都必须遵循固定线路而没有激情行程。因为数学问题的开放性很强,所以数学课堂上的教学中会有很多的不确定性。而且学生也在接受各种各样的有意义的信息,因此教师对他们的经验水平、知识积累乃至认知潜能等诸多方面都不可能预设到位,因此教师在课堂上实施的教学过程中充满了很大的挑战。这就要求教师用他的智慧将课堂中的一次次意外,转变成教学中的一次次亮 。
教师在备课时必须要考虑到不同的学生对同一问题可能会有不同的思考,对可能出现的问题准备相应的解决方法。只有这样,当“意外”发生时才能从容不迫、应对自如。其次,教师还要有一双慧眼,透视课堂,敏锐捕捉“意外”中有价值的信息,并合理地利用到课堂中来,灵活地进行调整,让“意外”的课堂,不再“意外”。

