德育渗透与核心素养的“刚柔并济”
夏青


近日,再次细细品读徐云鸿老师《小学数学教学中德育渗透方法例谈》一文,感慨颇多。如果说数学知识是一堂数学课中可见的、具体的、刚性的现实目标,那么德育的渗透无疑是深藏在数学知识背后的飘香的、柔软的、更难能可贵的核心目标,两者的“刚柔并济”和相得益彰,无疑能够让我们的数学课堂花团锦簇。我以《求小数的近似数》一课为例,谈谈核心素养和德育目标的交融并进。
一、数形结合。理性与数感交错
(一)提出问题
教师:著名的科学家爱因斯坦曾经说过,提出一个问题比解决一个问题更重要。针对你们自己研究出的保留一位小数求近似数的方法,你能不能也提出问题,带领大家深入思考?
学生1:为什么保留一位小数要看百分位?
学生2:因为保留一位小数,要看下一位。
学生3:如果不看百分位,看其它的数位那不就乱了吗?
教师:看来同学们都坚持要看百分位,我们可以从3.47为例来研究研究。
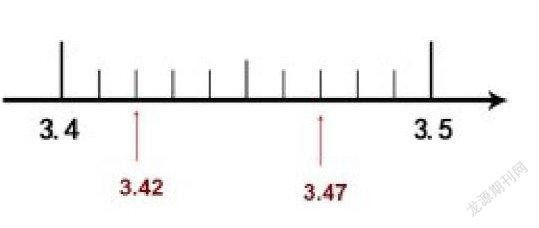
教师:把3.4和3.5之间,平均分成10份,找到3.47的位置。
(二)感悟四舍五入的道理
3.47约等于3.5,从图右看是为什么?学生1:3.47更靠近3.50学生2:3.47更接近一位小数3.5一些。
教师:那3.42呢?它保留—位小数约等于多少?学生1:它更接近一位小数3.4。学生2:百分位是2,就离3.4近一些了。教师:你能像老师这样再举几个两位小数吗?学生举出3.41、3.43、3.46等两位小数。教师:这些小数,哪些约等于3.47哪些约等于3.5呢?学生在寻找的过程中感悟四舍五入的道理。
(三)感悟只看百分位的道理
教师:我们再来找几个小数,3.471,它在哪儿?
学生:在3.47的右边一点点,在3.47和3.48之间。
教师:3.472呢?
学生1:在3.471的右边一点。
教师:3.479在哪儿?再添几个9呢?
学生1:它们越来越接近3.48,但是还是不到3.48。
教师:这些小数,它们有什么共同的特点?
学生1:它们保留一位小数求近似数的结果都是3.5。
学生2:它们从图上看都是接近一位小数3.5的。
学生3:它们都在3.47和3.48之间。
教师:这些小数,不管它们的千分位是几,也不管它们是几位小数,它们都在3.47-3.48之间,它们都更接近一位小数3.5,就是因为它们百分位上都是7。
教师:所以保留一位小数求近似数,只看百分位,把百分位上的数四舍五入就可以了。
二、联系实际。反思与数感并行
(一)身高保留整数
教师:篮球小巨人姚明身高2.26米,课前老师也让同学们用两位小数表示了自己的身高。
教师:我们班一位同学和姚明的身高差不多。
学生质疑。
教师:姚明身高和这位同学身高保留整数都是2米。
学生表示疑惑。
教师:这位同学可能有多高呢?我们来猜一猜吧!
学生1:有可能是1.6米,因为1.6保留整数约等于2。
生2:1.7米也约等于2米。
师:还有谁的身高保留整数也是约2米?
教师:(找到—位不举手的同学)你为什么没有举手?
学生:我的身高数保留整数约1米。
教师:同学们想一想,如果一个人的身高约2米,最低可能是多少,最高呢?
(二)身高保留一位小数
教师:看来一个人的身高约2米,他可能在1.5米到2.49米之间,我们班的这位同学,他的身高的确也在这个范围内,而且他的身高保留一位小数是1.6米,他可能有多高呢?
学生1:可能1.62米。
学生2:可能在1.6米到1.64米之间。
学生3:可能在1.55米到1.64米之间。
教师:揭晓答案:这位同学的身高是1.59米,果然在你们猜想的范围之内。
(三)对比反思
教师:同样是我们班这位同学的身高,约2米和约1.6米,哪个条件更好猜?
学生1:1.6米更好猜,因为它更精确。
学生2:1.6米更好猜,因为它更接近他的实际身高——些。
学生3:1.6米更好猜,因为它的范围更小。
教师:正如同学们分析的这样,约2米和约1.6米是把这位同学的身高精确到了不同的程度。
教师:在求近似数的时候,保留整数就是精确到个位,保留一位小数就是精确到十分位,保留两位小数就是精确到百分位,以此类推。
在这个过程中,学生反思近似数的取值范围,不断地经历尝试、反思、解释、重构的再创造过程,有利于提高学生的自我反思能力,达到了数感和反思能力的并行培养。
三、以点带面。规则与推理融合
(一)小组探究保留一位小数求近似数的方法
教师:怎样求一个小数的近似数呢?这就是我们今天要研究的主要内容。(板书:求小数的近似数)3.47保留一位小数约等于3.5,我们可以从保留一位小數开始研究。
教师:题纸上还有一些数据,快和你的同伴一起研究研究吧。
(二)汇报交流保留一位小数求近似数的方法
教师:怎样保留一位小数求近似数?
学生:我们学过求整数近似数的方法,所以,保留一位小数,看它的下一位,把它的下一位四舍五入。
学生3:3.47就是看百分位上的7,7>5,就要向前一位进一,所以约等于3.5。
教师:同学们能从整数求近似数的方法那里得到启发,应用在求小数的近似数,这是非常好的学习方法。
小组汇报:1.543=1.54 21.36156=21.4
学生:我们组举了一个例子,6.5431,因为百分位上是4,4<5,舍去,所以6.5431=6.5。
(三)总结求小数近似数的方法
教师:求近似数时,除了保留一位小数,还可以保留几位小数?
学生1:还可以保留两位小数,这时候就要看千分位,把千分位上的数字四舍五入。比如6.5431看千分位上的3就知道约等于6.54。
学生2:还可以保留整数,就是要保留到个位,看十分位。
学生3:3.47看十分位上的4,舍去,所以3.47=3。
学生4:保留整数就是精确到个位,要看十分位;保留一位小数就是精确到十分位,就要把百分位上的数字四舍五入;保留两位小数就是要精确到百分位,把千分位上的数字四舍五入。
学生5:还可以保留三位小数求近似数呢。
教师:怎样求一个小数的近似数?
学生:保留几位小数,就是精确到哪一位,就要看它的下一位,把它的下一位四舍五入。
(四)巩固应用,内化提升
学生汇报并订正。
学生有“四舍五入”法求整数的近似数的认知基础,对于求小数的近似数的方法探究,教师完全交给学生自主进行,他们在探究的过程中,主动调动了自己已有的知识经验,从而完成了对方法的迁移。从整数求近似数到保留一位小数求近似数,再到保留整数、保留两位小数求近似数,最后概括总结出求小数近似数的方法,学生在一步步的探究活动中,推理能力得到了提高。在整个推理过程中,学生理解数学规则的推导与总结过程,不仅懂得求小数的近似数的规则是怎样的,更明确了为什么要这样,在推理中培养恪守不渝的规则意识。诚然,如爱因斯坦所言:“当一个人把在学校学到的知识忘掉,剩下的就是教育。”我更愿意相信,德育渗透和核心素养若能纵横交错、相辅相成,必会让我们的数学课堂余音绕梁、韵味久远。
(责任编辑袁霜)

