扬克烘缸干燥能耗与干燥速率的软测量模型及应用

张维　李继庚　满奕　洪蒙纳

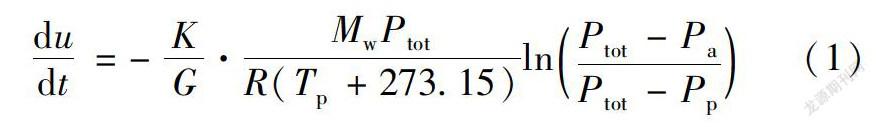
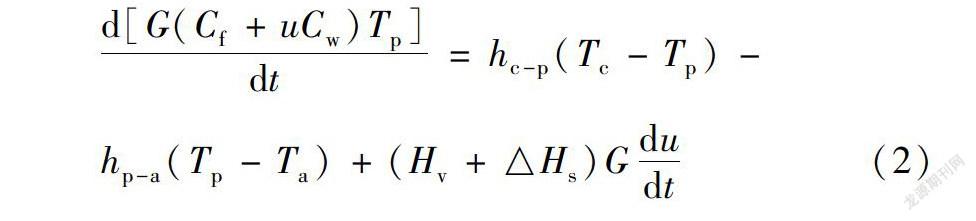
摘 要：目前生活用纸的干燥部常采用扬克烘缸干燥系统。本研究以环境温度和湿度以及容易采集的工艺操作参数为输入，建立了扬克烘缸干燥能耗与干燥速率的软测量模型，并将该模型在国内生活用纸纸厂广泛使用的BF系列纸机上进行了工业验证。结果表明，干燥速率与蒸汽流量平均误差分别在3%与5%以内。由此可见，本研究建立的软测量模型具有较好的可靠性，可为生产精细化管理提供科学依据。

关键词：生活用纸;干燥部;气罩;能量系统;优化;软测量

中图分类号：TS755

文献标识码：A

DOI：10.11980/j.issn.0254-508X.2019.05.007

Soft Sensing Model for Energy Consumption and Drying Rate of Yankee Cylinder and Its Application

ZHANG Wei LI Jigeng* MAN Yi HONG Mengna

（State Key Lab of Pulp and Paper Engineering， South China University of Technology， Guangzhou， Guangdong Province， 510640）

（*Email： jigengli@scut.edu.cn）

Abstract：The drying section has the highest energy consumption in tissue paper machine. Besides， it is also one of the key processes to control the quality of the products. How to reduce the energy consumption of drying section and ensure the product quality is a hot issue in the industry. Taking environment temperature and humidity and accessible operational parameters as model input， this study proposed a soft sensing model to simulate the energy consumption and drying rate of Yankee drying system which is a common drying method for tissue paper at present. The proposed model has been applied to BF paper machines under various production conditions. The results indicated that the average errors of drying rate and steam flow rate were are less than 3% and 5% respectively， it verifies the reliability and accuracy of the model， which could be used to supply the scientific basis for the drying process optimization.

Key words：tissue paper; drying section; air hood; energy system; optimization; soft sensor

隨着生活用纸产能快速增加以及近年来能源价格上涨，如何持续降低生活用纸生产过程能耗，提高能效水平是一个亟待解决的问题[1]。干燥部是造纸过程中能耗最大的工段，约占生产过程总能耗的60%以上，而干燥部的操作对其能耗有着极大的影响[2]。在生活用纸的实际生产中，通常是在成纸离开烘缸时，通过手感来判断纸张干度是否达标，从而调节蒸汽的压力和气罩送风的温度。而工艺调整过程中，具体应调整哪个参数、调节到多少等关键问题，往往基于经验判断，缺少系统的方案和科学的依据。因此，生产过程中会出现纸张的过干燥现象，从而造成了能量的浪费。而仅凭人工经验调节会导致一次调节不到位，造成多次调节，也使得产品的质量出现波动。

建立数学模型是进行干燥部参数优化的重要基础。李茜等人[3]在能量守恒模型的基础上对干燥部的送风温度进行优化，论证了干燥部建模优化的节能潜力。目前对于生活用纸纸机干燥部的建模，往往只针对某些特定型号或特定工艺的纸机。林治作[4]对生活用纸的干燥过程建立了水分和温度分布模型，并在纸机的设计工况下进行了纸张干度验证。Di Marco等人[5]对生活用纸纸机的干燥部建立了完整的数学模型，并利用模型研究了一系列不同操作参数下干燥部的能源利用效率。然而要得到一个可进行参数优化的数学模型，确保模型的泛化能力，对模型进行大规模的验证是必要的。而验证的难点在于模型的边界条件难以测量和控制，例如，气罩的送风温度较高，相对湿度较低，在线湿度传感器测量误差极大而且高温条件下易损坏，难以进行直接调节。烘缸表面由于喷淋药液的存在，只能使用误差较大的非接触式仪器测量烘缸表面温度。

本研究以江门某纸厂为案例，在现有的纸张干燥研究的基础上，提出了一种适用生活用纸纸机干燥部的机理建模方法。在给出操作参数和环境温、湿度的条件下，模拟出干燥部的蒸汽流量与干燥速率，使用能源管理系统积累的大量数据进行了批量验证，为生产过程节能提供科学依据。

1 扬克烘缸干燥系统

生活用纸纸机的干燥部一般是由扬克烘缸和使用循环热风的气罩组成。如图1所示，压榨后的湿纸幅通过托辊转入烘缸，纸幅在烘缸上的大部分行程被气罩覆盖，进行蒸发脱水和排出湿气。纸幅出气罩后，通过刮刀离开烘缸。气罩的通风系统一般分为干侧和湿侧两个部分，有的两侧结构相同，有的干侧气罩并无强制通风。各种气罩布局的生活用纸纸机，共同之处在于都存在如图2所示的循环通风管道。如图2所示，鼓风机将热风（1）送入气罩，吹向纸幅进行强制冲击干燥，气罩缝隙吸入车间的冷空气（2）、蒸发掉纸幅中的水分（3），气罩排出的湿空气（4）被分为两部分。一部分由排风机抽出（5），另一部分湿空气（6）回用，与新鲜风（7）混合，混合风（8）使用蒸汽加热器进行加热，通过鼓风机进入气罩，形成循环。

2 模型建立

纸幅的水分和能耗是干燥部最重要的指标。为了求解纸幅水分和烘缸对纸幅的传热，对纸幅干燥过程进行模拟是必要的，而水分的蒸发传质受到气罩通风的影响。鉴于以上特点，生活用纸纸机干燥部的建模过程可划分为以下三个部分。

2.1 纸幅干燥动力模型

纸张干燥动力的相關研究表明[6]，空气和纸幅表面的水蒸气压力差构成了蒸发传质的动力，见式（1）。

dudt=-KG·MwPtotR（Tp+273.15）lnPtot-PaPtot-Pp（1）

式中，u为纸幅的局部含水量，即单位质量的绝干纸幅所携带的水分，kg水/kg绝干纤维;Tp为纸幅的局部温度，℃;G为纸幅单位面积上的绝干纤维质量，kg/m2;t为时间，s;K为纸幅和空气之间的对流传质系数，m/s ;Mw为水的摩尔质量，kg/mol;R为理想气体常数，J/（mol·K）; Ptot、 Pa、Pp分别为总压、空气中水蒸气分压与纸幅表面的水蒸气分压，Pa。

根据能量守恒定律，单位时间、单位面积内纸幅能量的变化等于纸幅热传导、对流传热、蒸发水分带走的热量以及克服吸附阻力的热量之和，如式（2）所示。

d[G（Cf+uCw）Tp]dt=hc-p（Tc-Tp）-

hp-a（Tp-Ta）+（Hv+△Hs）Gdudt（2）

式中，hc-p为烘缸表面与纸幅间的传热系数，W/（m2·℃）;Tc为烘缸表面温度，℃;hp-a为纸幅和空气之间的对流传热系数，W/（m2·℃）;Ta为纸幅所处环境空气的温度，℃;Hv为纸幅中蒸发的水蒸气焓值，J/kg;△Hs为纸幅水分的吸附热，J/kg;Cf、Cw分别为纤维和水的比热，J/（kg·℃）。

由于纸幅温度与水分相互耦合，对式（2）左边进行变量分离得到纸幅温度方程。为了求解不同干燥区域内纸幅的水分与温度，使用dLv代替式（1）与式（2）中的dt，最终得到纸幅水分与温度分布方程，见式（3）～式（4）。

dudL=-KG·v·MwPtotR（Tp+273.15）lnPtot-PaPtot-Pp

（3）

dTpdL=hc-p（Tc-Tp）-hp-a（Tp -Ta）+（Hv+△Hs -Cw Tp）G·vdudLG·v（Cf+uCw）

（4）

式中，L为纸幅局部在烘缸经过的纵向行程，描述纸幅的位置，m;v为烘缸线速度，m/s。

水蒸气的焓值由温度决定并可通过线性回归得到。吸附热由纸幅温度与含水量决定[4]，见式（5）～式（6）。

△Hs=0.10085R1-φMwφu1.0585（Tp+273.15）2（5）

φ=1-exp（-47.58u1.87-0.10085Tpu1.0585）（6）

式中，φ为纸幅表面的相对湿度。

烘缸表面温度受蒸汽与纸幅温度共同影响，且随位置变化。根据能量守恒定律，烘缸表面的局部温度可按式（7）计算。

hs-c（Ts-Tc）=hc-p（Tc -Tp）（7）

式中，hs-c为烘缸内的蒸汽到烘缸表面的总传热系数，W/（m2·℃），作为待定参数;hc-p为烘缸与纸幅间的接触传热系数，W/（m2·℃）;Ts为烘缸蒸汽温度，℃。

接触传热系数与纸幅含水量线性相关，其取值参考文献[6]，如式（8）所示。

hc-p=955u+700（8）

对于纸幅和空气的对流传热系数，可通过努塞尔数初步求解，见式（9）。

hconv=Nu·λaLconv（9）

式中，hconv为对流传热系数，W/（m2·℃）;Nu为努塞尔数;λa为纸幅所处环境的空气热导率，W/（m·℃）;Lconv为对流特征长度，m。

努塞尔数的计算在不同情形下采用不同的方法，根据L的值在不同干燥区切换。在气罩外，纸和空气传热传质类似于湍流流过平板的情形。气罩外的努塞尔数Nuout根据式（10）计算[7]。

Nuout=0.037Re0.81Pr1+2.443Re-0.1（Pr2/3-1）（10）

式中，Pr为空气的普朗特数;Re为雷诺数。

在气罩内的高温气流冲击干燥不同于气罩外的情形。气罩内的努塞尔数Nuin可参考金属板在高温气流冲击下的经验公式[8]，如式（11）所示。

Nuin=f′0.9505[3.649-（0.03455+4.812f′）hd′1+60.47f′

×[0.90+0.101+0.056939（Ta/100℃）3]Re0.772Pr1/3（11）

式中，f′为修正后的气罩喷嘴开孔率;h为喷嘴到纸幅的距离，m;d′为修正后的喷嘴直径，m。

式（9）的对流传热系数可直接用于气罩外，而气罩内的传质速率较高，对传热产生了影响，须对传热系数进行校正[9]，见式（12）～式（13）。

hp-a=hconvEeE-1（12）

E=-G·vdudLCvhconv （13）

式中，E为传质过程中单位面积上热容流率与修正前传热系数之比;Cv为水蒸气比热，J/（kg·℃）。

根据传热系数计算传质系数的类比法被广泛应用于纸幅干燥[5，10]，见式（14）～式（15）。

K=hp-aρa CaLe-2/3（14）

Le=λaρaCaDwa（15）

式中，ρa为纸幅所处环境的空气密度，kg/m3;Ca为空气比热，J/（kg·℃）;Le为刘易斯数;Dwa为水在空气中的扩散系数，m2/s。

最终，整个干燥部的干燥速率根据纸幅干燥模型的解uE确定，如式（16）所示。

R=（uA-uE）G·v3600LAE（16）

式中，R为干燥部的干燥速率，kg/（m2·h）; uA、uE分别为纸幅在烘缸起点与终点的含水量，kg水/kg绝干纤维; LAE为干燥区的纵向总长度，m。

2.2 气罩通风模型

为了求解气罩内的水蒸气压，采用了一种迭代计算的建模方法，模擬纸机从开机到稳定的过程。利用操作参数数据与环境温度、湿度对气罩送风湿度，以及通风系统各点的温度、湿度、焓值和质量流量进行软测量。

能量物料守恒计算过程中所需的湿空气的密度和焓值的计算如式（17）～式（19）所示。

P=PtotXX+0.622（17）

ρ=0.0034843（P-0.3779Ptot）T+273.15（18）

H=103[1.01T+（2501+1.85T）X]（19）

式中，P为空气中的水蒸气分压，Pa;Ptot为总压，Pa; X为空气湿度，kg水/kg干空气; ρ为空气密度，kg/m3;T为空气温度，℃;H为空气焓值，J/kg干空气。

如图2 所示，以干燥部湿侧为例，根据输入数据，已知气罩送风与排风机排风的体积流量， 空气温度T1，T7，环境空气湿度X7。使用迭代法求解气罩内的送风空气湿度X1，对其初始值进行假设，如式（20）所示。

X（1）1=X7（20）

式中，X（1）1为第一次迭代时气罩的送风湿度，kg水/kg干空气。

根据进出气罩空气能量质量守恒，气罩排风的温湿度与流量由气罩送风和漏风以及蒸发水量决定，见式（21）～式（23）。

m（1）41+X（1）4=m（1）11+X（1）1+m21+X2（21）

m（1）4X（1）41+X（1）4=m（1）1X（1）11+X（1）1+m2X21+X2+m3（22）

m（1）4H（1）41+X（1）4=m（1）1H（1）11+X（1）1+m2H21+X2+m3H3+QAC

（23）

式中，m为质量流量，kg/s;QAC为图1中ABC弧面区域内烘缸对纸幅的传热速率，W。

对于气罩缝隙漏风m2的计算，以气罩平衡率HB为基准确定漏风量，即从管道进出气罩的绝干空气质量流量之比。气罩平衡率可通过人工测量不同工况下的管道空气流量确定，见式（24）。

HB=m1（1+X4）（1+X1）m4（24）

整个通风系统干空气质量守恒，见式（25）。

m（1）71+X（1）7=m（1）51+X（1）5-m21+X2（25）

根据管道内空气能量质量守恒，求出混合风的质量流量、湿度和焓值，见式（26）～式（28）。

m（1）81+X（1）8=m（1）41+X（1）4-m（1）51+X（1）5+m（1）71+X（1）7（26）

m（1）8X（1）81+X（1）8=m（1）4X（1）41+X（1）4-m（1）5X（1）51+X（1）5+m（1）7X（1）71+X（1）7（27）

m（1）8H（1）81+X（1）8=m（1）4H（1）41+X（1）4-m（1）5H（1）51+X（1）5+m（1）7H（1）71+X（1）7（28）

加热前后湿度不变，见式（29）。

X（2）1=X（1）8（29）

将X（2）1按照（21）～式（29）的过程进行多次迭代后，通风系统各点的温湿度达到稳定，整个通风系统各点的温湿度、质量流量、焓值和密度均可解出。

2.3 干燥部能耗模型

烘缸供热分为三部分：压榨区外烘缸传给纸幅的热量、压榨区内传给纸幅的热量以及烘缸壳体的热损失。烘缸消耗的蒸汽流量见式（30）。

∫EAhs-c（Ts-Tc）WdL+Qroll+

（Ts-Tenv）∑Acihci=ΔHcmc（30）

式中，W为纸幅幅宽，m; Tenv为环境温度;Aci、hci分别为烘缸未覆盖纸幅的部分壳体上第i块区域的传热系数和面积， ∑Acihci可视为烘缸的热损失系数，作为待定参数，W/℃;ΔHc为烘缸蒸汽到冷凝水的焓变，J/kg;mc为烘缸消耗的蒸汽流量，kg/s;Qroll为在压榨区内烘缸对纸幅的传热速率，W。

对于压榨区内传热Qroll的计算，由于压榨处接触面积极小，且毛毯传热系数难以确定，为简便计算，假定传热量全部用于湿纸幅升温，见式（31）。

Qroll=vWG（TA-T0）（Cf+uACw）（31）

式中， T0为纸幅上烘缸前的温度，℃;TA为纸幅经过压榨后的温度，℃。

气罩加热器能耗包括空气加热能耗和换热器对环境传热，见式（32）。

m1（H1-H8）1+X1+（T1-Tenv）∑Ahihhi=ΔHhmh（32）

式中， ΔHh为空气加热器中蒸汽的焓变，J/kg;T1为气罩送风温度，℃;mh为气罩空气加热消耗的蒸汽流量，kg/s。∑Ahihhi 为气罩的热损失系数，W/℃。

3 模型应用与验证

模型的参数包含测量数据和待定参数。其中，纸机固定的尺寸数据和可视为常数的过程参数如湿纸幅的初始温度与含水量数据较为稳定，可使用测量值，测量数据如表1所示。而传热系数与热损失系数难以直接确定，使用输入输出数据进行逼近。

模型的输入数据包含车间环境的温度、湿度，气罩送风的温度，鼓风机与排风机的空气体积流量，烘缸内蒸汽压力，以及车速和定量数据，从能源管理系统中采集。在5个月时间段内，以1 min为间隔采集原始数据。剔除异常工况和重复数据后，对模型进行求解。选取320数据进行模型参数调整，将干燥速率的模拟值与真实值对比反复调整hs-c的大小，根据气罩蒸汽流量的对比调整∑Ahihhi的大小，根据烘缸蒸汽流量的对比调整∑Acihci的大小，待定参数的调参结果如表2所示。

使用80组数据进行检验。操作参数的不断调整，导致蒸汽流量和干燥速率发生了变化。模型准确地预测到了干燥部能耗与干燥速率随着操作参数变化的趋势和数值。

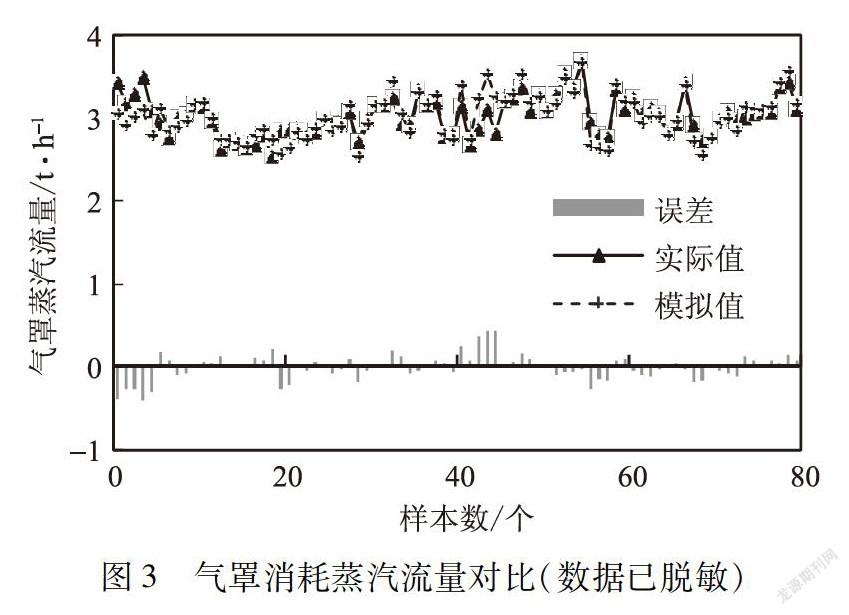
气罩蒸汽流量的对比效果如图3所示。从图3可以看出，数值和变化趋势都得到了较好的模拟，误差在0.5 t/h以下，平均绝对百分误差为4.62%，烘缸蒸汽流量的对比效果如图4所示，平均绝对百分误差为3.30%。可见在不同时段、不同工况下，干燥部蒸汽流量的数值和变化趋势得到了较好的模拟，满足了根据操作参数预测蒸汽流量的需要。

实际生产中对成纸干度的调整操作需要科学的指导，然而由于缺少湿纸干度的在线测量，模型对成纸干度的模拟并不理想。但干燥速率也能在一定程度上反映干燥部的蒸发脱水能力。通过干燥速率的模拟值与实际值的对比，来衡量模型在各种工况下对蒸发脱水能力的模拟精度。干燥速率对比效果如图5所示，平均绝对百分误差为2.55%，基本上能在各工况下为干度调整提供指导，在此基础上加以微调即可精确控制成纸干度。

4 结 论

使用迭代计算的方式求解通风系统的温度和湿度，与纸幅干燥动力模型相结合，对生活用纸纸机的扬克烘缸气罩干燥系统进行了建模。将模型应用在BF型纸机上，使用了5个月的生产运行数据进行调参和对比验证，干燥速率误差为2.55%，烘缸和气罩的蒸汽流量平均绝对百分比误差在5%以内，验证了模型的有效性。能对干燥部模型进行大批量验证的关键在于实现了气罩送风湿度的软测量，从而将模型的边界条件扩展到了操作参数层面。对干燥部蒸汽流量和干燥速率的软测量，可为生产过程中的节能操作提供指导，为最佳工艺参数的探讨和节能分析提供理论依据。

参 考 文 献

[1] YANG Runshan. Study on energy consumption optimization of tissue machine drying section based on improved genetic algorithm[D]. Xian： Shaanxi University of Science and Technology， 2018.

楊润珊. 基于改进遗传算法的生活用纸机干燥部能耗优化研究[D]. 西安： 陕西科技大学， 2018.

[2] LI Jigeng， KONG Lingbo， Liu Huanbin. Dryer Section Energy System Measurement and EnergySaving Potential Analysis for a Paper Machine[J]. Measurement and Control， 2012， 45（8）： 239.

[3] LI Qian， PANG Xiao， TANG Wei， et al. Based on PSO Algorithm to Optimiz the Supply Air Temperature of Dryer Section Hood Ventilation System[J]. China Pulp and Paper， 2016， 35（8）： 57.

李 茜， 庞 肖， 汤 伟， 等. 基于粒子群算法优化干燥部气罩通风系统送风温度[J]. 中国造纸， 2016， 35（8）： 57.

[4] ;LIN Zhizuo. Research on modeling of paper sheet drying[D]. Guangzhou： South China University of Technology， 2012.

林治作. 纸幅干燥过程建模研究[D]. 广州： 华南理工大学， 2012.

[5] Di Marco， Paolo Frigo， Stefano Gabbrielli， et al. Mathematical modelling and energy performance assessment of air impingement drying systems for the production of tissue paper[J]. Energy， 2016， 114： 201.

[6] CHEN Xiaobin， DONG Yunyuan， ZHENG Qifu， et al. Kinetic Model and Numerical Simulation of Paper Drying Process Base on Boundary Layer Theory[J]. Transactions of China Pulp and Paper， 2017， 32（3）： 37.

陈晓彬， 董云渊， 郑启富， 等. 基于“边界层”理论的纸张干燥动力学模型及其数值仿真[J]. 中国造纸学报， 2017， 32（3）： 37.

[7] Lars Nilsson. Heat and mass transfer in multicylinder drying Part I： Analysis of machine data[J]. Chemical Engineering and Processing， 2004， 43（12）： 1547.

[8] Pertti Heikkil， Nenad Milosavljevic. Influence of impingement temperature and nozzle geometry on heat transferexperimental and theoretical analysis[J]. Drying Technology， 2003， 21（10）： 1957.

[9] Anders Ottosson， Lars Nilsson， Jonas Berghel. A mathematical model of heat and mass transfer in Yankee drying of tissue[J]. Drying Technology， 2017， 35（3）： 323.

[10] John H Lienhard IV， John H Lienhard V. A heat transfer textbook[M]. USA： Phlogiston Press， 2011.CPP