向量在立体几何解题中的妙用

谢紫霞

摘 要：向量是数学中一个非常重要的量，向量在不同的数学问题中有着不同的用法和作用，在解决几何问题中展示出了特殊的妙用。向量在几何中的应用由点线面，再到立体几何，其中有着多种存在的意义，了解向量在立体几何中的用法及意义有助于将较为复杂的几何问题转化为简单的问题，对于解决复杂的立体几何有着重要的存在意义。本文就来探讨向量在立体几何中的妙用。

关键词：向量;立体几何;解题;妙用

引言：立体几何是由点、线、面构成的几何形体，我们生活中随处可见各种各样的立体几何。立体几何同样是数学学科中的重要知识，巧妙的解决立体几何问题是灵活应用数学知识的表现。通过立体几何的构成，我们认识到立体几何中存在着较多的向量。不管它是圆柱、棱柱，还是圆锥、棱锥，我们都可以通过寻找立体几何中存在的向量关系，找到计算和证明立体几何的方式。并且，通过寻找有效的向量关系，还能够简化问题的思路，将复杂的问题简单化，从而巧妙灵活的解决数学问题。

一、立体几何中常见的向量类型

（一）直线的方向向量

与经过已知点直线平行的直线的非零向量就叫做直线的方向向量，表示为=。

（二）平面的法向量

在同一空间，如果直线l垂直于平面a，直线l的方向向量为，向量交租平面a的法向量，表示为·=0[1]。

二、利用向量解决立体几何问题的优点

（一）解题思路清晰化

立体几何的难点在于没有具体的数据，因此最简单的方法就是将立体几何代数化。立体几何代数化使点、线、面之间的关系清晰化，解题思路自然也就清晰化了。而向量关系就是解决立体几何非代数化的关键，因此，向量也是使立体几何解题思路清晰化的关键。

（二）简化运算过程

立体几何中的很多关系往往需要较长的推理才能得出，借助向量法解决一些需要推理的立体几何问题，可以直接通过向量为立体几何建立关系，使得立体几何的解题思路直观明了，简化了推理点、线、面关系的过程。因此，巧用向量解决立体和问题可以简化运算过程。

（三）复杂问题简单化

不少立体几何问题的证明看似复杂，实则存在着很多直线、平面以及角度之间的关系，此时借助辅助线可以为寻找立体几何直线、平面以及角度之间的关系搭建桥梁，通过向量来顺利的找到其中的关系，从而确立解题思路。简而言之，向量的引入可以使较为抽象的立体几何空间关系有了明确的坐标、代数关系等，同时使立体几何的空间关系具体化，使简单的问题复杂化。

三、立体几何中常见向量妙用

向量在立体几何中的妙用主要是借助平行关系、垂直关系、夹角问题以及距离问题体现，还经常会借助辅助线、坐标系、假设代数关系等完成，巧妙之处在与为看似復杂的几何空间创建解决实际几何问题需要的关系，并通过各种相关关系之间的联系来相互转化和推理。以下是常见的向量在几何问题中的妙用。

（一）平行关系

如下图1正方体所示，长房体的棱长为1，M和N分别为A1B1和BB1的中点，求直线AM和CN所成角的余弦值。解题思路如下：

先使两条异面直线的平行线相交，确定目标三角形，然后用余弦定理来计算三角形的夹角，从而求出异面直线所成的角的角度。在利用平行关系解此题是需要分别作出B1E、NF、FC3条辅助线，以直观的观察该正方体中的平行关系。

（二）垂直关系

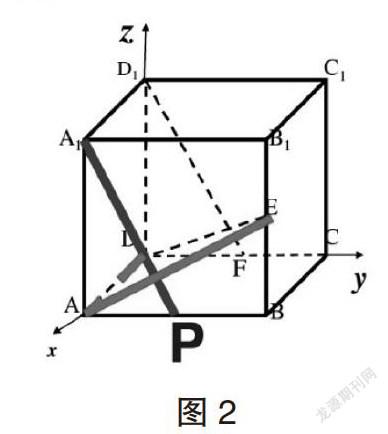
如下图2正方体所示，E点和F点分别是BB1和CD的中点。求证D1F⊥平面ADE。由于在该正方体问题中没有明确的代数关系，因此首先应该假设一个明确的代数关系，然后应用向量正交基底解决该问题[2]。解题思路如下：

设正方体棱长为1，以，，为单位正交基底，并以建立D为顶点建立坐标系

（1，0，0），=（1，1，），=（0，，-1）

所以·=0，·=0

所以，⊥

又因为DA与DE相交形成D点

所以⊥平面ADF

结语：综上所述，立体几何问题都可以通过寻找平行关系、垂直关系、夹角问题、距离问题等向量关系来实现。向量在立体几何中的应用可以使立体几何相对简单化，同时找到解决问题的对应关系，是巧妙解决立体几何的有效途径。因此建议教师在教授立体几何时重点引导学生探索向量关系，主动思考向量与立体几何之间的关系，这有助于学生加深对于立体几何的理解问题。

参考文献

[1]王博文.向量在立体几何解题中的妙用[J].中学课程资源，2012（09）：55-57.

[2]刘福亮.向量法在立体几何解题中的妙用[J].数学学习与研究，2015（13）：83.