活力课堂：让思维向纵深处漫溯

陶士梅 朱耀峰

摘要：“三角形的三边关系”是操作与推理探究成分很强的学习内容。这一课，设计了“激趣引入，明确要求”“动手操作，合作探究”“实例研析，初步验证”“推理尝试，深入论证”“应用练习，巩固升华”等教学环节，体现学习情感鲜活、思维发展深活、教学设计新活的特点。

关键词：活力课堂学习情感思维发展三角形的三边关系

【教学内容】

苏教版小学数学四年级下册第77—78页。

【教学目标】

1.经历操作实验、举例推理等过程，探索三角形三边之间的关系，理解并能运用三角形三边之间的关系解释和解决简单问题。

2.在操作实验过程中，感受探索和验证规律的途径和方法，培养观察、比较、判断、推理、归纳、概括等思维能力和学习能力。

3.在学习过程中，积累活动经验，体验规律探索的乐趣和挑战性，提高学习兴趣和积极性。

【教学重点】

三角形三边之间关系的探索和验证。

【教学难点】

在操作中培养观察、比较、判断、不完全归纳等思维能力;体验实例验证和推理论证等探索规律的方法，积累数学活动经验。

【学具准备】

为每个学生准备一个信封（里面装有半圆柱形状的小棒3根）、一张小组探究学习单。

【教学过程】

一、激趣引入，明确要求

师昨天的课堂上我们重新认识了一位图形老朋友——三角形。如果给你一支笔，让你任意画出一个三角形，会画的同学请举手。

（学生热情高涨，都举起了手。）

师（课件出示3根小棒）如果给你3根小棒，让你围出一个三角形，不会围的同学请举手。

（没有学生举手，每个人都确信自己能围出一个三角形。）

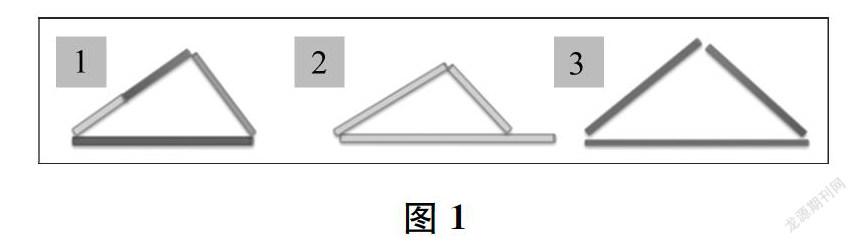
师老师最欣赏自信的孩子了！不过，数学学习很多时候光有自信是不够的！在动手操作之前，老师有一点要提醒大家，（课件出示图1）这些图形，我们都认为是不合格的。为什么？

生因为第一个三角形用了4根小棒。

生第二个图形中，小棒浪费了，没有充分利用。

生第三个图形接头处没有相连。

师由于我们的小棒有点粗，严格地讲，应该让小棒内侧的三条线段首尾相接才可以。

（课件示范正确围法。）

[评析：三角形对于学生来说，太熟悉了。任意画一个三角形，学生是完全可以做到的，因为此时的三边长度是由学生自己根据需要任意选择的。但是，用任意三根小棒围出一个三角形，是不确定的（学生在学习之前是不知道其中的学问的）。教师充分抓住学生的这种“轻敌”心理，激发操作热情;同时，为了避免操作后汇报时注意力的分散，教师提前展示几种错误的操作方法，将正误标准及操作要领讲得很清楚，防患于未然，可谓用心良苦！]

二、动手操作，合作探究

（学生动手操作：用教师课前给定的3根小棒围三角形。）

师已经成功地围成三角形的同学请举手。

（多数学生很得意地举手;部分学生很着急又不好意思，因为没有围出三角形。）

师（故作狐疑）还真有人没有围出来啊？！别着急，谁能勇敢地带上小棒到前面来展示一下，让大家帮忙看看到底哪儿出问题了？

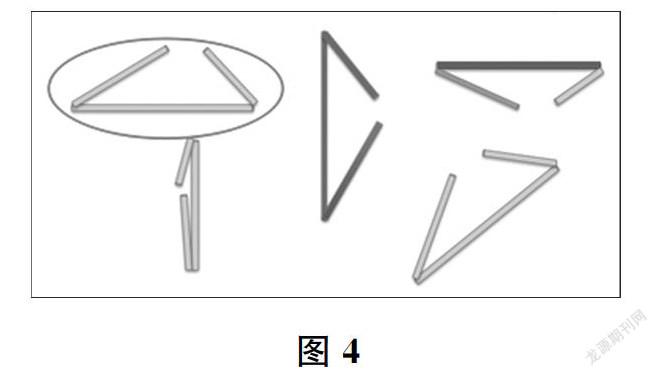
生（展示操作，如图2、图3）我的小棒长度分别是8厘米、5厘米和2厘米，够不着。

师大家看出来了吗？这些小棒围不出三角形，问题出在小棒上！

师（课件出示图4）仔细观察一下我们刚才摆出的这些图形。从表面上看，它们大小、形状、方向都不同，但是其实，它们骨子里是——

生一样的！

师既然是一样的，咱们就留下一组研究研究。（选择8厘米、5厘米、2厘米的一组小棒）观察并思考一下：为什么它们无法完成首尾相接呢？

生因为5厘米和2厘米太短了。

生因为5厘米和2厘米加起来还没有8厘米长。

师如果允许你将小棒变长，你想把它们怎么变？

……

师谁来概括总结一下，只要让小棒怎么变，就可以围成三角形？

生只要让两条短边之和大于最长边。

师有不同想法吗？

生我覺得两条短边之和等于最长边也是可以的。

师（故作惊喜）有哪位同学手上有这样的小棒，上来试一试，让大家眼见为实吧！

生我用10厘米、6厘米和4厘米的3根小棒，撑不起来，围不成。

生两条短边还是要大于最长边，才可以围成三角形。

师现在，如果老师再任意给你三根小棒，让你围出一个三角形，你还敢像刚才那样说一定能围成吗？

生（齐摆手）不敢。

师不敢恰恰说明你们的智慧增长了！

[评析：操作过程是认知活动的“脚手架”。为了让学生把在操作过程中获得的感悟提炼并清晰地表达出来，教师以一个例子为重点，引导学生在反复的操作变化中透过现象看本质，感受问题的一致性;再鼓励学生自主变化小棒的长度使其可以围成三角形，他们会不由自主地让“两条短边长度之和大于最长边”。至此，“三角形中两条短边长度之和大于最长边”的规律水到渠成，为后面得出“三角形任意两边长度的和大于第三边”的规律奠定了坚实的逻辑基础。]

三、实例研析，初步验证

师刚刚我们通过自己的操作发现了三角形三边关系的一条规律，但是课本上的结论和我们发现的有点不一样。请打开课本第77页看一看。

（学生看书后，教师课件出示：三角形任意两边长度的和大于第三边。师生齐读三遍。）

师你能理解这句话的意思吗？为了方便表达，我们把三边分别标上①②③，请说说你对这句话的理解。

生①+②>③。

生②+③>①。

生①+③>②。

师虽然课本上是这么说的，但是课本上的就一定对吗？你打算怎么做？

生我打算找一个三角形，把它任意两边的长度加起来，看看是不是真的大于第三边。

师找一个？

生多找一些。就用我们刚才围出来的三角形。

师如果我们全班的三角形三边长度都符合这句话，那就说明——

生这句话是对的。

师（引导语气）如果——

生出現一个不符合的，那就说明这句话是错误的。

师为了方便汇报，我们可以做一个表格，把探索结果填到表格里。

（课件出示下页表1。学生验证得出结论：没有找到反例，三角形任意两边长度之和大于第三边。）

师既然没有找到反例，那我们就暂时确定“三角形任意两边长度的和大于第三边”。

[评析：举例验证、不完全归纳是探索规律的重要途径。这一环节的精彩之处在于：学生完全是探索的主人而不是被动的操作工——方法学生自己思考，步骤学生自己安排，结果学生自己判断。在这样的训练下，学生的探索能力得到了有效的培养，质疑能力和批判性思维也得到了很好的激发。]

四、推理尝试，深入论证

师举例验证确实是探索数学规律的重要途径，但是，数学规律的探究还有很多其他的方法。今天，老师给大家推荐的方法是：（同步板书）推理论证。你认为推理是怎么一回事？

生推理应该就是讲道理。

生推理就是通过一个道理推出另一个道理。

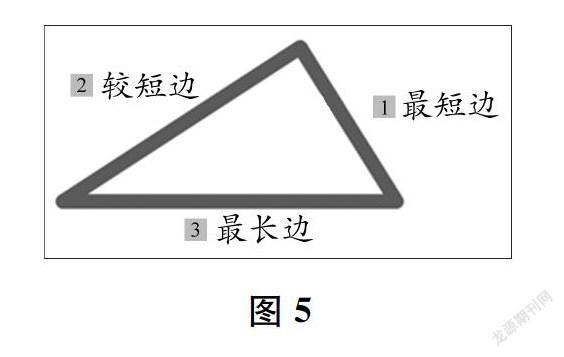
师大家猜得一点也没错！数学上的推理就是根据现有确定的结论或规律，通过讲道理推出其他结论或规律的过程。你能试着利用我们刚刚研究的规律“两条短边之和大于最长边”来证明“任意两边长度的和大于第三边”吗？（课件出示图5）为了便于表达，我们把三角形的三边分别叫作最短边、较短边、最长边。

生最短边+较短边>最长边，这是我们刚才操作得出的结论;最长边+最短边>较短边，因为最长边本身已经大于较短边了，再加上一个最短边，肯定大于较短边;最长边+较短边>最短边，因为无论最长边还是较短边，都大于最短边，所以它们的和一定大于最短边。

师推导得真棒！现在谁来总结一下？

生“三角形任意两边长度的和大于第三边”这句话是对的。

师你感觉举例验证和推理论证，哪一种得到的结论更周密一些？

生举例，因为举例更简单。

生举例虽然简单，但是说不定有的例子举不到，会影响我们对结果的判断。推理是表示任意长度都成立的，所以推理得到的结论更周密一些。

（全班学生自发鼓掌。）

师其实，这个结论也可以从反面来论证。如果任意两边的长度的和不大于第三边，会出现什么情况呢？

（学生自发开始讨论。）

生我们是这样想的：两条短边的和如果小于最长边，则一定是围不成三角形的;两条短边的和即使等于最长边，也是围不成三角形的。那么两条短边的和就只有大于最长边，才能围成三角形。

师真了不起，你们都学会从反面来证明了！总共三个方面，排除掉两个方面，从而得出结论：两条短边之和大于最长边才能围成三角形。

[评析：例证法非常直观、易于操作，但是有时无法把例子举全，会缺少足够的说服力。为了培养学生理性、科学的论证能力，教师让学生尝试推理论证。然后，通过比较，让学生在思辨中感受推理论证的合理性与确定性，为以后学习数学证明做铺垫。更难能可贵的是，在教师的引导下，学生的思考中还出现了“反证法”的雏形。]

五、应用练习，巩固升华

（一）呼应已有旧知

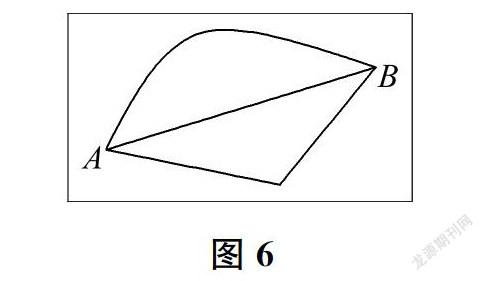
师（课件出示图6）这幅图大家还有印象吗？谁能用今天学到的知识来解释一下，为什么从A点到B点中间这条线路最短。

生因为三角形的两边之和大于第三边，所以线段AB是最短的。

师原来，我们今天学习的“三角形两边之和大于第三边”与之前学习的“两点之间线段最短”是可以互相印证的。

（二）寻找第三根小棒

师“三角形任意两边长度的和大于第三边”这条规律虽然看起来简单，但是用起来却并不是那么容易的。想不想挑战一下自己？

生想！

（课件出示图7。）

生（急忙回答）1—13都可以。

生1绝对不可以，1加4小于10！

生应该是7到13都可以。

师（微笑）同学们，数学的魅力就在于不让你一眼就看透。我们别着急，先安静思考一会或小组讨论一下，再做决定。好吗？

（学生热烈讨论。不一会儿，小手一片。）

生（得意）我们组认为答案是7、8、9、10、11、12、13。

（其他学生放下了手。）

师这么多答案要想一个不漏地说出来，说实话，还真不是容易的事。谁有什么好办法吗？

生我觉得应该分开来想：如果第三根小棒当短边，它的长度加上4要大于10，所以必须是大于6的数;如果第三根小棒当长边，10加上4要大于它的长度，所以只能是小于14的数。所以答案是大于6而小于14。

师你们都会分类思考了，真厉害！把第三条边当作短边，它必须大于6厘米;把第三条边当作长边，它必须小于14厘米。小数也可以吗？

生小数也可以。从6.1到13.9都可以。

师由于我们才认识一位小数，所以这个结论目前是对的。我们今天的收获真大啊！

（三）截出第三根小棒

师如果现在只有两根小棒，一根长10厘米，另一根长4厘米，要将其中一根截成两段，得到3根小棒，围成一个三角形，你打算截哪一根？截成几厘米和几厘米的两段？

生把4厘米的分成两段肯定不行，因为它本身就比10厘米短。只有把10厘米的分成两段。

师你们认同他的想法吗？

（学生点头。）

师你打算将10厘米长的这根分成怎样的两段呢？是不是随意分都可以？小组合作完成。

（学生小组活动。）

生把10厘米分成4厘米和6厘米。

生把10厘米分成3厘米和7厘米。

生不可以，3厘米加上4厘米等于7厘米了。把10厘米分成5厘米和5厘米是可以的。

师难道只有这两种分法吗？课后我们继续研究。

[评析：教师充分挖掘、利用“围三角形”题目的思维含量，将看似简单的题目教出了一波三折。出示题目后，教师利用学生急于表现但思维不够严密的特点，由着他们发表意见，暴露错误;然后，引导学生“先安静思考或小组讨论”，从而不仅培养他们深度思考、谨慎言行的习惯，同时也让他们感觉到合作交流是解决问题的重要方式。有学生一口气报出所有答案后，教师又引导学生思考得到这些答案的方法。数学学习不仅仅是结果的达成，最重要的是思维过程的展示、碰撞与交流。在“寻找第三根小棒”和“截出第三根小棒”环节，学生在激烈的思维碰撞与交流中将探究延伸到课外，教师的引导无痕而智慧。]

六、回顾总结，积累经验

教师从数学知识、数学方法和数学活动经验积累三方面引导学生回顾总结，养成反思习惯，既将获得的新知纳入原有的认知结构中，又提炼数学思想方法，积累数学活动经验。

【教学总评】

“三角形的三边关系”是操作与推理探究成分很强的学习内容。综观全课，教师很好地驾驭了教材，调动了学生。整节课充满活力，精彩不断，具体有以下几个鲜明特点：

第一，学习情感鲜活。活力课堂的表现在于学生学习情感的鲜活。这节课上，学生有初次面对问题的自信满满，有摆不成三角形的郁闷和困惑，有找到原因的激动和欣喜，有发现规律的急于表现，有善于思辨的胸有成竹。这些情感的真实流露证明，学生的学习是主动而真实的。

第二，思维发展深活。活力课堂的重要表现在于学生思维发展的深活。在一波三折的探索中，教师将学生的思维逐渐推进至纵深处。学生首先通过操作，发现规律：两条短边之和大于最长边。教师推进：“课本上的结论和我们发现的有点不一样。”“课本上的就一定对吗？你打算怎么做？”学生的批判性思维被激发，已有的活动经验被激活。紧接着举例验证，教师又让学生“推理论证”。尝试成功之后，教师没有浅尝辄止，而是引导学生进行比较，促使学生深刻感悟“推理论证”的合理性和确定性。“反证法”的出现更是思维灵活与创新的展现……整节课，学生的思维主动活跃，不断深入且愈发严谨，称得上是一节非常好的思维训练课。

第三，教学设计新活。活力课堂的表现还在于教学设计的新活。教师把教材内容按难度分解成逻辑紧密的几个环节和层次，环环孕伏，层层深入。第一层次，实验操作发现“两条较短边之和大于最长边”;第二层次，举例和推理得出“任意兩边长度之和大于第三边”;第三层次，通过反证由直观到抽象、由特殊到一般，确认获得结论的合理性;第四层次，设计富有挑战性、科学性、严谨性，有力度、有深度的练习，使学生及时应用巩固所得。