浅谈高等数学中的反证法

张莹

摘要：反证法在数学中是一种非常重要的间接证明方法，它被称为“数学家最精良的武器之一”，又称为归谬法、背理法。反证法亦称“逆证”。其不仅是一种论证方法，对提升学生创新性思维能力与概念思维能力具有积极作用，从某种角度可以说，反证法还是一种思维方式，其还能拓展学生的解题思路，从而使学生形成良好的数学思维。反证法在中学数学中有着广泛的应用，如今学生在运用反证法解题中，基础一般的学生会受到思维能力的限制，如果能恰当的使用反证法，在一些有难度的题目上也许能够得到解决。所以本文首先会叙述反证法的产生，具体阐述反证法的定义，即反证法的概念、分类、科学性，介绍逆证在中学数学中的实际运用并论述了逆证应用的具体需要注意的一些问题。

关键词：反证法;中学数学;应用;

1 引言

反证法是间接论证的方法之一，亦称“逆证”、矛盾证法。它在中学数学中有着不可替代的重要作用，一般来说，当学生遇到不容易或者不能从正面进行证明的题目时，则可以尝试运用反证法进行证明。反证法弥补了直接证明的不足，完善了证明方法，运用反证法可以培养和提高学生的逆向思维能力和创造思维能力，把不可能转化为可能。教师应要结合熟悉的生活实例和典型的数学例题，帮助并引导学生了解反证法继而使用反证法，然后运用反证法拓宽学生解决问题的思路。

2 反证法的产生

2.1古希腊的反证法

在南意大利学派的影响下，其主张“一切事物都是整数”，数学知识是可靠和准确的。但随着第一次数学危机的发生，自根号二的发现，使希腊人重新审视了他们自己的数学，从此他们对以数作为基础的几何做了舍弃的选择。首次的数学发展遇到的暂时困难，使其没有办法只信靠直观与图形，所以，西方为代表的数学须以证明为主来证明数学。而他们要的是准确性的数学。它以演绎、逻辑为表现的形式。可以推断其意指算的数学与证明的数学恰恰不同。希腊人认为数值计算是几何证明之后的一个应用，他们更注重演绎与证明，指出“不要近似”，也就是要达到“明确的形式证明和公理的使用”[1] 。

2.2 中国古代数学中的反证法

对推理演绎的证明，在我国的古代数学领域缺少重视，尽管人们发现一些逻辑规律，例如在魏晋时期的雄辩之风，大多数的反驳用到了归谬法，这里的归谬法就是举反例，刘徽受当时的影响，在他的《九章算术注》中，归谬论证法被多次使用，刘徽在证明某些公式是错误的时候，用的方法都是反驳，并且是成功的，符合逻辑规律的。墨家学派创始人也曾利用反证法，比如违反矛盾律的谬误：“学之益也，说在诽者。”。利用“学习无益”不是真的证明，得出“學习有益”是真命题。归谬法也是反证法中的一种方法，但因为中国逻辑学的不完善，在指出明确运用反证法的用法上是少之又少，与西方差别甚大。

3 反证法在中学数学中的应用

这类命题用直接证明是有一定难度的或者说结论的反面比结论本身更容易证明，因为已知条件以及由已知条件推出的结论比较少，在这种题目中能够运用的定理、定义、公理也比较少，此时我们会选择用反证法来进行证明[4] 。

已知：

求证：

证明：假设与不平行，

则AB与CD相交于点P

，即、即，

过点有2条不一样的直线同平行，然而此矛盾于几何学的重要公理之一——平行公理，所以，假定与不平行不成立.

故.

【分析】让学生知道这种类型题是不能直接证明的，这要从问题的反面出发，否定命题结论，即AB与CD不平行，那么它们肯定相交，交点为P，因为过点P就有两条直线AB、CD都平行于EF，这显然与平行公理矛盾，产生矛盾的原因是假设错误。所以AB与CD不相交，则只能平行，问题得证[5] 。

例1 平面与直线的交点为，在平面内，过点画出直线、、，，那么是否正確，若正确，请求证。

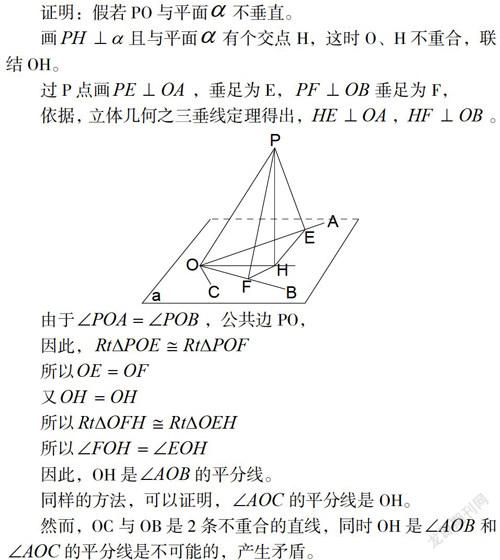
证明：假若PO与平面不垂直。

画且与平面有个交点H，这时O、H不重合，联结OH。

过P点画，垂足为E，垂足为F，

依据，立体几何之三垂线定理得出，，。

由于，公共边PO，

因此，

所以

又

所以

所以

因此，OH是的平分線。

同样的方法，可以证明，的平分线是OH。

然而，OC与OB是2条不重合的直线，同时OH是和的平分线是不可能的，产生矛盾。

【分析】本道题若从正面进行证明，根据题目所给条件所能借助的公理定理有限，则只能尝试从反面去思考，这道题由于不能直接证明，不妨先假设PO不垂直平面，以此为条件再结合相关定理得到与客观事实不符合的结论，这说明假设“PO不垂直平面”错误，那么假设的反面就是正确的，即，故原命题结论成立。

4 总结

数学是一门非常能考验人的思维逻辑的学科，我们认为反证法是一种数学思想，在数学证明里，反证法（逆证）是一种重要的解题方法。学会运用反证法，能锻炼我们各方面的能力如观察力、逆向思维能力、辨别能力、创造能力等，从而养成良好的学习习惯，这对我们学习其他数学知识有很大的帮助。

参考文献：

[1] 嘉程程，李超峰.浅谈反证法及应用[J].农家参谋，2019（15）：231.

[2] 田俊英.关于数学分析中适于用反证法证明的问题类型分析[J].景德镇学院学报，2019，34（03）：21-25.

[3] 王璐.“反证法”的教学策略[J].初中数学教与学，2019（11）：1-3+18.

[4] 李群.高等代数解题中反证法实例研究[J].黑河学院学报，2019，10（01）：212-214.

[5] 刘爱琴.一个数学问题的反证法证明与推广[J].中学数学教学参考，2018（33）：28-29.

[6] 雷紫同.浅谈“反证法”在高中数学的应用[J].数学学习与研究，2018（18）：116.

（作者单位：无锡机电高等职业技术学校）